разносторонний треугольник Это трехсторонний многоугольник, где у каждого разные размеры или длины; по этой причине ему дается название лестница, что на латыни означает скалолазание.
Треугольники — это многоугольники, считающиеся простейшими в геометрии, потому что они образованы тремя сторонами, тремя углами и тремя вершинами. В случае разностороннего треугольника, поскольку он имеет все разные стороны, это означает, что его три угла также будут разными..
- 1 Характеристика разносторонних треугольников
- 1.1 Компоненты
- 2 свойства
- 2.1 Внутренние углы
- 2.2 Сумма сторон
- 2.3 Несовместимые стороны
- 2.4 Неконгруэнтные углы
- 2.5 Высота, медиана, биссектриса и биссектриса не совпадают
- 2.6 Ортоцентр, барицентр, стимулятор и околицентр не совпадают
- 2.7 Относительные высоты
- 3 Как рассчитать периметр?
- 4 Как рассчитать площадь?
- 5 Как рассчитать высоту?
- 6 Как рассчитать стороны?
- 7 упражнений
- 7.1 Первое упражнение
- 7.2 Второе упражнение
- 7.3 Третье упражнение
- 8 ссылок
- Характеристики разносторонних треугольников
- компоненты
- свойства
- Внутренние углы
- Сумма сторон
- Непоследовательные стороны
- Несогласованные углы
- Высота, медиана, биссектриса и биссектриса не совпадают
- Ортоцентр, барицентр, стимулятор и центр окружности не совпадают
- Относительные высоты
- Как рассчитать периметр?
- Как рассчитать площадь?
- Как рассчитать высоту?
- Как рассчитать стороны?
- обучение
- Первое упражнение
- Второе упражнение
- Третье упражнение
- Масштаб в математике
- Понятие масштаба
- Определение масштаба на карте
- Решение задач на масштаб
- Урок математики по теме «Масштаб»
- Ход урока
- 1. Мотивация к учебной деятельности
- 2. Актуализация знаний обучающихся
- 3. Сообщение темы урока, цели урока
- 4. Открытие нового знания
- 5. Физкульминутка
- 6. Первичное осмысление и применение изученного
- 7. Применение знаний и способов действий
- 8. Подведение итогов урока
- 9. Домашнее задание
- 10. Рефлексия
- 💥 Видео
Видео:Находим масштабСкачать

Характеристики разносторонних треугольников
Масштабные треугольники являются простыми многоугольниками, потому что ни одна из их сторон или углов не имеет одинаковую меру, в отличие от равнобедренных и равносторонних треугольников..
Поскольку все его стороны и углы имеют разные измерения, эти треугольники считаются неправильными выпуклыми многоугольниками.
По амплитуде внутренних углов разносторонние треугольники классифицируются как:
- Шкала прямоугольник треугольник: все его стороны разные. Один из его углов прямой (90 или ) а остальные резкие и с разными мерами.
- Шкала тупого угла треугольника: все его стороны разные, и один из его углов тупой (> 90 или ).
- Шкала острого угла треугольника: все его стороны разные. Все его углы острые ( или ), с разными мерами.
Еще одной характеристикой разносторонних треугольников является то, что из-за несовместимости их сторон и углов они не имеют оси симметрии.
компоненты
Медиана: линия, которая выходит из средней точки одной стороны и достигает противоположной вершины. Три медианы совпадают в точке, называемой центроид или центроид.
Биссектриса: это луч, который делит каждый угол на два угла одинакового размера. Биссектрисы треугольника совпадают в точке, называемой incentro.
Посредник: это сегмент, перпендикулярный стороне треугольника, который начинается в середине этого. В треугольнике три медиатрицы, совпадающие в точке, называемой окружностью.
Высота: линия, идущая от вершины к противоположной стороне, а также эта линия перпендикулярна этой стороне. Все треугольники имеют три высоты, которые совпадают в точке, называемой ортоцентром.
Видео:Масштаб. Как найти масштаб карты. Как найти отрезок на карте или расстояние на местности #масштабСкачать

свойства
Масштабные треугольники определены или идентифицированы, потому что они имеют несколько свойств, которые их представляют, возникших из теорем, предложенных великими математиками. Это:
Внутренние углы
Сумма внутренних углов всегда равна 180 или .
Сумма сторон
Сумма мер двух сторон всегда должна быть больше меры третьей стороны, a + b> c.
Непоследовательные стороны
Все стороны разносторонних треугольников имеют разные размеры или длины; то есть они неуместны.
Несогласованные углы
Поскольку все стороны разностороннего треугольника различны, их углы также будут разными. Однако сумма внутренних углов всегда будет равна 180º, и в некоторых случаях один из ее углов может быть тупым или прямым, в то время как в других все его углы будут острыми.
Высота, медиана, биссектриса и биссектриса не совпадают
Как и любой другой треугольник, в составной части есть несколько отрезков прямых линий, составляющих его, например: высота, медиана, биссектриса и биссектриса..
Из-за особенностей его сторон, в этом типе треугольника ни одна из этих линий не будет совпадать в одной.
Ортоцентр, барицентр, стимулятор и центр окружности не совпадают
Поскольку высота, медиана, биссектриса и биссектриса представлены различными отрезками прямых линий, в разностороннем треугольнике точки встречи — ортоцентр, центроцентр, стимулятор и окрицентр — будут находиться в разных точках (они не совпадают).
В зависимости от того, является ли треугольник острым, прямоугольным или разносторонним, ортоцентр имеет разные местоположения:
а. Если треугольник острый, ортоцентр будет внутри треугольника.
б. Если треугольник является прямоугольником, ортоцентр будет совпадать с вершиной прямой стороны.
с. Если треугольник тупой, ортоцентр будет находиться снаружи треугольника..
Относительные высоты
Высоты относительно сторон.
В случае разностороннего треугольника эти высоты будут иметь разные измерения. Каждый треугольник имеет три относительных высоты и для их расчета используется формула Герона.
Видео:Масштаб. 6 класс.Скачать

Как рассчитать периметр?
Периметр многоугольника рассчитывается по сумме сторон.
Так как в этом случае разносторонний треугольник имеет все стороны с различной мерой, его периметр будет:
P = сторона a + сторона b + сторона c.
Видео:Построение высоты в тупоугольном и прямоугольном треугольниках. 7 класс.Скачать

Как рассчитать площадь?
Площадь треугольников всегда рассчитывается по одной и той же формуле, умножая основание на высоту и деля на два:
Площадь = (база * ч) ÷ 2
В некоторых случаях высота разностороннего треугольника неизвестна, но есть математическая формула, предложенная математиком Хероном, для расчета площади, зная измерение трех сторон треугольника..
- a, b и c, представляют стороны треугольника.
- sp, соответствует полупериметру треугольника, то есть половине периметра:
В случае, если у вас есть измерение только двух сторон треугольника и угла, который сформирован между ними, площадь может быть рассчитана путем применения тригонометрических соотношений. Итак, вы должны:
Площадь = (сторона * ч) ÷ 2
Где высота (h) — произведение одной стороны на синус противоположного угла. Например, для каждой стороны площадь будет:
Видео:Масштаб - задачи и примеры. Математика 6 классСкачать

Как рассчитать высоту?
Поскольку все стороны разностороннего треугольника различны, вычислить высоту с помощью теоремы Пифагора невозможно.
Из формулы Герона, которая основана на измерениях трех сторон треугольника, можно вычислить площадь.
Высота может быть очищена от общей формулы площади:
Сторона заменяется измерением стороны a, b или c.
Другой способ вычислить высоту, когда известно значение одного из углов, состоит в применении тригонометрических соотношений, где высота будет представлять ногу треугольника..
Например, когда известен противоположный угол к высоте, он будет определяться синусом:
Видео:Площадь треугольника. Как найти площадь треугольника?Скачать

Как рассчитать стороны?
Если у вас есть мера двух сторон и угол, противоположный этим, можно определить третью сторону, применив теорему косинусов.
Например, в треугольнике AB показана высота относительно сегмента AC. Таким образом, треугольник делится на два прямоугольных треугольника.
Для вычисления c-стороны (отрезок AB) применяется теорема Пифагора для каждого треугольника:
- Для синего треугольника вы должны:
Поскольку m = b — n, оно заменяется:
с 2 = ч 2 + б 2 (б — н) 2
с 2 = ч 2 + б 2 — 2 млрд + н 2 .
- Для розового треугольника вы должны:
час 2 = а 2 — N 2
Он заменяется в предыдущем уравнении:
с 2 = а 2 — N 2 + б 2 — 2 млрд + н 2
с 2 = а 2 + б 2 — 2BN.
Зная, что п = а * cos C, заменяется в предыдущем уравнении, и получается значение стороны c:
с 2 = а 2 + б 2 — 2b* в * потому что C.
По закону косинусов стороны могут быть рассчитаны как:
- в 2 = б 2 + с 2 — 2b* с * потому что.
- б 2 = а 2 + с 2 — 2-й* с * потому что B.
- с 2 = а 2 + б 2 — 2b* в * потому что C.
Есть случаи, когда размеры сторон треугольника неизвестны, но их высота и углы, которые образуются в вершинах. Для определения площади в этих случаях необходимо применять тригонометрические соотношения.
Зная угол одной из его вершин, ноги идентифицируются и используется соответствующее тригонометрическое соотношение:
Например, катет AB будет противоположен углу C, но прилегает к углу A. В зависимости от стороны или катета, соответствующих высоте, другая сторона очищается, чтобы получить значение этого.
Видео:Масштаб. Практическая часть. 6 класс.Скачать

обучение
Первое упражнение
Рассчитайте площадь и высоту разностороннего треугольника ABC, зная, что его стороны:
решение
В качестве данных приведены измерения трех сторон разностороннего треугольника.
Поскольку у вас нет значения высоты, вы можете определить площадь, применяя формулу Герона..
Сначала рассчитывается полупериметр:
sp = (8 см + 12 см + 16 см) ÷ 2
Теперь значения в формуле Герона заменены:
Зная площадь, можно рассчитать относительную высоту на стороне b. Из общей формулы, очистив ее, вы получите:
Площадь = (сторона * ч) ÷ 2
46, 47 см 2 = (12 см * ч) ÷ 2
ч = (2 * 46,47 см 2 ) ÷ 12 см
h = 92,94 см 2 ÷ 12 см
Второе упражнение
Учитывая разносторонний треугольник ABC, меры которого:
- Сегмент AB = 25 м.
- Сегмент БК = 15 м.
В вершине B образуется угол 50 °. Рассчитайте относительную высоту в сторону с, периметр и площадь этого треугольника.
решение
В этом случае у вас есть меры двух сторон. Для определения высоты необходимо рассчитать измерение третьей стороны.
Поскольку задан угол, противоположный заданным сторонам, можно применить закон косинусов для определения измерения стороны переменного тока (b):
б 2 = а 2 + с 2 — 2-й*с * потому что B
б = переменный ток.
б 2 = (225) + (625) — (750) * 0,6427
б 2 = (225) + (625) — (482,025)
Поскольку у вас уже есть значение трех сторон, рассчитайте периметр этого треугольника:
P = сторона a + сторона b + сторона c
Р = 15 м + 25 м + 19, 18 м
Теперь можно определить площадь, применяя формулу Герона, но сначала необходимо рассчитать полупериметр:
Измерения сторон и полупериметра заменяются формулой Герона:
Наконец, зная площадь, можно рассчитать относительную высоту на стороне c. Из общей формулы, очистив ее, вы должны:
Площадь = (сторона * ч) ÷ 2
143,63 м 2 = (25 м * ч) ÷ 2
ч = (2 * 143,63 м 2 ) ÷ 25 м
h = 287,3 м 2 ÷ 25 м
Третье упражнение
В разностороннем треугольнике ABC сторона b имеет размер 40 см, сторона c имеет размер 22 см, а в вершине A образуется угол 90 или . Рассчитайте площадь этого треугольника.
решение
В этом случае даны измерения двух сторон разностороннего треугольника ABC, а также угла, образованного в вершине A.
Для определения площади нет необходимости вычислять меру стороны а, поскольку через тригонометрические соотношения угол используется для ее нахождения.
Так как угол, противоположный высоте, известен, это будет определяться произведением с одной стороны и синусом угла.
Подставляя в формулу площади, вы должны:
Площадь = (40 см * 22 см * сен 90) ÷ 2
Площадь = (40 см * 22 см * 1) ÷ 2
Видео:КАК НАЙТИ МАСШТАБ КАРТЫ? Примеры | МАТЕМАТИКА 6 классСкачать

Масштаб в математике
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Видео:КАК НАЙТИ ВЫСОТУ ТРЕУГОЛЬНИКА? ЕГЭ и ОГЭ #shorts #егэ #огэ #математика #профильныйегэ #треугольникСкачать

Понятие масштаба
Чтобы понять, что такое масштаб в математике нужно вспомнить тему отношений чисел и пропорций.
Масштаб — это дробь, где в числителе единица, а в знаменателе то число, которое показывает во сколько раз уменьшено расстояние на плане местности, чем на самой местности.
Другими словами, масштабом называют отношение длины отрезка на карте к длине соответствующего отрезка на местности.
- Например, одна тысячная (1:1000) означает, что все расстояния на местности уменьшены в тысячу раз. Чем больше число в знаменателе дроби, тем больше уменьшение и тем больше охват территории.
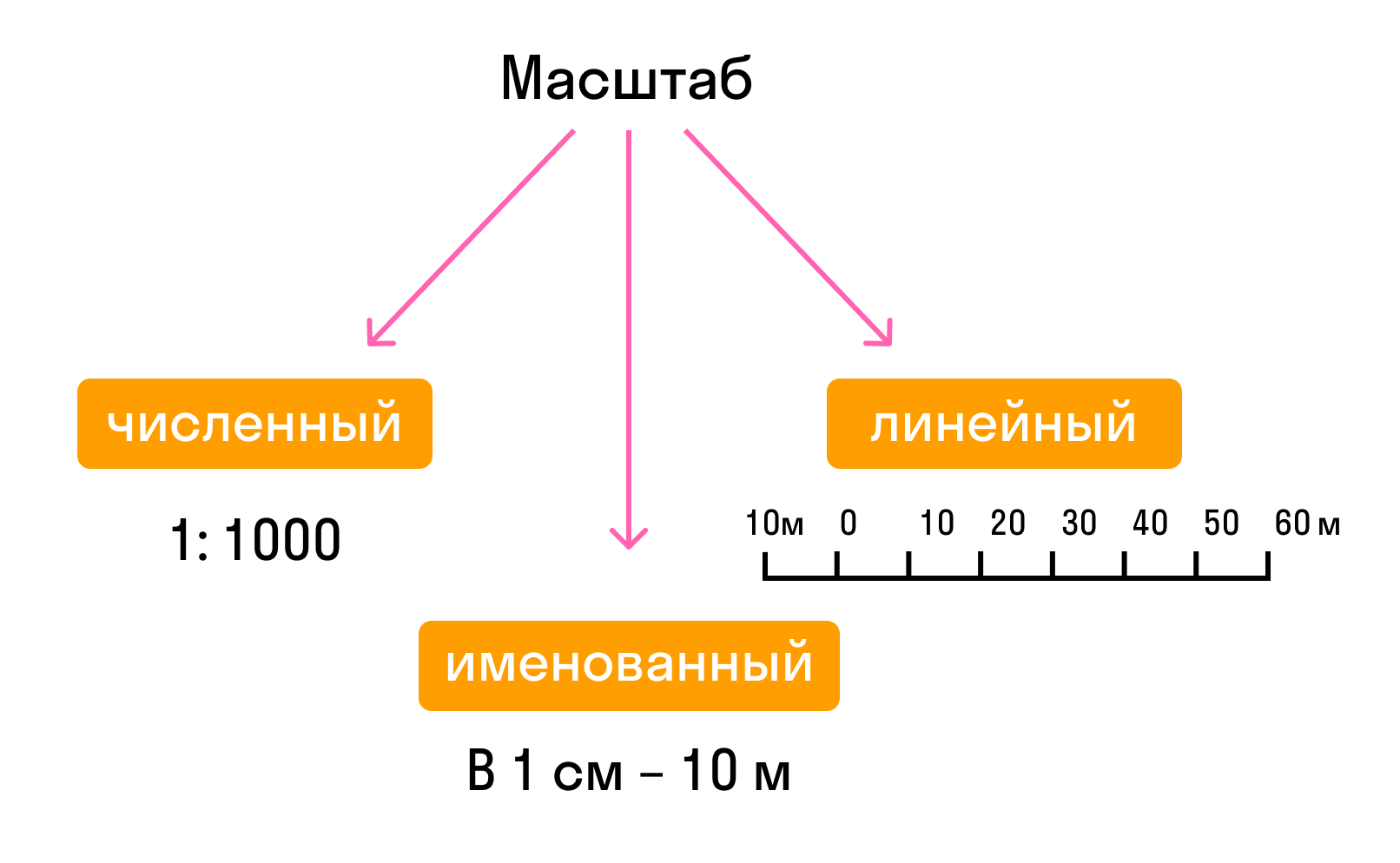
Масштаб бывает трех видов:
- численный, выражается в числах 1:1000;
- именованный, выражается словами, то есть см переводим в м: в 1см 10м, 10м — это величина масштаба;
- линейный, зная величину масштаба, можно определить расстояния.
Курсы обучения математике помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Видео:Периметр треугольника. Как найти периметр треугольника?Скачать

Определение масштаба на карте
На математике в 6 классе обязательно будут задания, как найти масштаб карты. Разберемся в этом вопросе.
Нужно потратить очень много сил, чтобы изобразить дом в натуральную величину, поэтому и придумали такой инструмент, как масштаб. Ведь намного проще описать большой объект в рисунке, чертеже или макете.
Масштаб — это отношение размера изображения к размеру изображаемого объекта.
Масштаб карты — это отношение длины отрезка на карте к его действительной длине на местности.
На карте Российской Федерации указан масштаб (1 : 500 000). Читается это так: карта сделана в масштабе одна пятисот тысячная. Такой масштаб значит, что в 1 см на карте помещается 500 000 см реального расстояния. То есть отрезок на изображении в 1 см соответствует отрезку на местности в 5 км. А если взять отрезок в 3 см, то на местности этот отрезок составит 15 км.
Численные масштабы карт и соответствующие им масштабы на местности:
Масштаб 1 : 100 000
- 1 мм на карте — 100 м (0,1 км) на местности
- 1 см на карте — 1000 м (1 км) на местности
- 10 см на карте — 10000 м (10 км) на местности
Масштаб 1 : 10000
- 1 мм на карте — 10 м (0,01 км) на местности
- 1 см на карте — 100 м (0,1 км) на местности
- 10 см на карте — 1000 м (1 км) на местности
Масштаб 1 : 5000
- 1 мм на карте — 5 м (0,005 км) на местности
- 1 см на карте — 50 м (0,05 км) на местности
- 10 см на карте — 500 м (0,5 км) на местности
Масштаб 1 : 2000
- 1 мм на карте — 2 м (0,002 км) на местности
- 1 см на карте — 20 м (0,02 км) на местности
- 10 см на карте — 200 м (0,2 км) на местности
Масштаб 1 : 1000
- 1 мм на карте — 100 см (1 м) на местности
- 1 см на карте — 1000 см (10 м) на местности
- 10 см на карте — 100 м на местности
Масштаб 1 : 500
- 1 мм на карте — 50 см (0,5 метра) на местности
- 1 см на карте — 5 м на местности
- 10 см на карте — 50 м на местности
Масштаб 1 : 200
- 1 мм на карте — 0,2 м (20 см) на местности
- 1 см на карте — 2 м (200 см) на местности
- 10 см на карте — 20 м (0,2 км) на местности
Масштаб 1 : 100
- 1 мм на карте — 0,1 м (10 см) на местности
- 1 см на карте — 1 м (100 см) на местности
- 10 см на карте — 10м (0,01 км) на местности
Видео:Масштабы в геодезии. Поперечный, линейный, численный. Как читать и как пользоваться.Скачать

Решение задач на масштаб
Для закрепления темы решим несколько математических задач на масштаб за 6 класс.
Пример 1. Длина отрезка на карте равна 8 см. Найти длину соответствующего отрезка на местности, если масштаб карты равен 1 : 10 000.
8 см — это 1 часть
8 * 10 000 = 80 000 (см) — это 10 000 частей
80 000 см = 800 м
Пример 2. Расстояние между двумя городами 400 км. Найти длину отрезка, который соединяет эти города на карте, выполненный в масштабе 1:5000000.
400 км = 400 000 м = 40 000 000 см
40000000 : 5000000 = 40 : 5 = 8
Пример 3. Расстояние от Москвы до Санкт-Петербурга по прямой составляет примерно 635 км. По автотрассе протяженность маршрута 700 км. Во сколько раз надо уменьшить это расстояние, чтобы его можно было изобразить в виде отрезка длиной в 14 см?
Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Урок математики по теме «Масштаб»
Разделы: Математика
Цели:
- формирование понятия масштаба и его применении на практике,
- формирование учебной деятельности (мотивация, поиск способов действий, прогнозирование, проверка и самопроверка).
- способствовать развитию умения делать выводы на основе собственных наблюдений, сравнения, обобщения, использования личного опыта; развивать логическое мышление.
- способствовать развитию навыков самоконтроля и самооценки, развитию математической грамотности
- способствовать воспитанию любви к своему городу, области, Родине.
Задачи:
- расширить знания о масштабе, придать им практическую направленность (использование для решения текстовых и геометрических задач);
- развивать образное мышление, а также умение сравнивать, анализировать, обобщать, делать выводы, находить пути решения проблемного вопроса.
- воспитывать ответственное отношение к труду.
- закрепить навыки, связанные с преобразованием величин;
Тип урока: урок открытия новых знаний.
Методы обучения: объяснительно-иллюстративный, словесный, проблемный, практический.
Форма организации деятельности учащихся на уроке: фронтальная, коллективная, индивидуальная.
Элементы технологий, используемые на уроке: интерактивная, ИКТ, обучение с использованием опорных схем.
Оборудование: презентация, раздаточный материал для проведения практической работы (карта Курской области, Обоянского района, план квартиры), модель здания и автомобилей, глобус, модель кристаллической решетки, изображения простейших микроорганизмов в увеличенном виде, линейка, нитка, лист самооценки.
Оформление доски:– «Мало знать, надо и применять, мало хотеть, надо и делать» (И.Гете)
План урока
- Мотивация к учебной деятельности
- Актуализация знаний обучающихся
- Сообщение темы урока, постановка цели урока
- Открытие нового знания
- Физ. минутка
- Первичное осмысление и применение изученного материала
- Применение знаний и способов действий
- Подведение итогов урока
- Домашнее задание
- Рефлексия
Видео:Как найти площадь треугольника без формулы?Скачать

Ход урока
1. Мотивация к учебной деятельности
Проверяется подготовленность классного помещения и готовность обучающихся к уроку, наличие принадлежностей для работы на уроке, заранее на столы раскладывает раздаточный материал.Учитель:Приветствуем друг друга.
Ребята, вы любите сказки? Вспомните сказку про Марью- Искусницу. Король задал задачу «Пойди туда, не знаю куда. Принеси то, не знаю что». Задача была решена? Да конечно, как и в любой сказке все можно решить и эта задача не осталась без решения.
Ребята, я хотела бы задать вам вопрос, но ответ на него вы мне дадите по окончании урока.Как вы думаете, можно ли объять необъятное и увидеть невидимое?
2. Актуализация знаний обучающихся
Учитель: У вас на столах лежит лист самооценки. Свою работу вам нужно оценить. Ребята, на предыдущих занятиях мы с вами познакомились с понятиями «Отношения» и «Пропорции». Вспомним основные понятия. (фронтальный опрос)(Приложение 3)
Что такое отношение двух чисел? (это частное двух чисел)
Как можно записать отношение чисел? (с помощью знака : или в виде дроби)
Что показывает отношение чисел? (какую часть составляет одно число от другого или во сколько раз одно число больше другого).
Устный счет: Найдите ошибки в записи



Что называют пропорцией? (Равенство двух отношений)
В чем заключается основное свойство пропорции? (В верной пропорции произведение крайних членов равно произведению средних членов)
Устная работа: Проверьте, верна ли пропорция? 4:9=9:4; 
Учитель: Вспомните, а где мы применяли пропорции? (Для решения уравнений, задач на прямую и обратную пропорциональные зависимости, простейших задач на проценты).
Как вы думаете, где в жизни вам решение таких задач, с помощью составления отношений, пропорций, может пригодиться? (при приготовлении блюд, для расчёта продуктов; в строительстве для определения необходимого количества техники или людей, в архитектуре и др.; на уроках химии при решении задач, физики для работы с формулами и т.д.).
Сегодня на уроке мы познакомимся ещё с одной областью применения отношений и пропорций.
3. Сообщение темы урока, цели урока
Учитель: Ребята, обратите внимание на те предметы, которые находятся перед вами. (дом, фотография, машинки, глобус, карта модель атома и кристаллической решетки, схема микроорганизмов.) Какое отношение эти предметы имеют к математике.
Что общего между всеми этими предметами? (их размеры не соответствуют действительности, одни увеличены, а другие уменьшены в одно и то же число раз)
При изучении каких предметов вы могли узнать об уменьшении или увеличении объектов? (на географии, природоведении)
А как определить, во сколько размеры изображения отличаются от реальных размеров?
С каким понятием мы сегодня будем работать на уроке? (Масштаб)
Сегодня на уроке мы будем работать над темой «Масштаб»
Открываем тетради, записываем тему урока: Масштаб. (Приложение 1, слайд 1)
Давайте вместе с вами сформулируем цели нашего сегодняшнего урока.
Что мы должны сегодня на уроке узнать? (познакомиться с понятием масштаб), (научиться решать задачи с использованием этого понятия, найти практическое применение новому понятию)
Вывод: Сегодня на уроке мы должны узнать, что такое масштаб и найти его практическое применение в жизни. Мы попытаемся ответить на вопрос для чего необходимо изучить эту тему? Убедимся, какое важное практическое применение имеет материал сегодняшнего урока.
4. Открытие нового знания
Учитель: Античная мудрость гласит: «Незнающие пусть научатся, а знающие вспомнят еще раз». Ребята подготовили небольшое сообщение, послушайте.
Ученики: (историческая справка) 1. Изображение различных предметов — рисунки появились как средство общения между людьми еще до создания письменности. С тех пор как научились возводить сначала простейшие, а потом более сложные сооружения, мастера стали использовать при строительстве рисунки, а затем и чертежи. (Слайд 2) Сохранившиеся наскальные рисунки свидетельствуют о зарождении картографического способа передачи информации, который совершенствовался в течение многих веков. При строительстве жилищ, крепостей и других сооружений появились первые чертежи, которые назывались «планами». Эти чертежи обычно выполнялись в натуральную величину непосредственно на земле, на месте будущего сооружения . Для построения таких чертежей были созданы первые чертежные инструменты — деревянный циркуль-измеритель и веревочный прямоугольный треугольник . В дальнейшем такие планы-чертежи стали выполнять на пергаменте, дереве и холсте в уменьшенном виде. На чертежах старались показать как форму, так и размеры предметов. (Слайд 3)
Учитель: Само слово “масштаб” пришло к нам из немецкого языка. Maс означает: “мера”, штаб означает “размер”, что уже говорит о связи с математикой. Слово “масштаб”, придя из немецкого языка, хорошо прижилось в нашей речи.
Ученик: 2. Люди всегда рисовали уменьшенные изображения местности, причем разные участки изображения уменьшали произвольно, в разной степени. Поэтому старинные чертежи местности не дают возможности понять, например, каково расстояние между берегами реки, чему равна длина реки и т.д. Одной из древнейших карт (за 2500 лет до н.э.) считается так называемый вавилонский чертеж, выполненный на глиняной табличке.(Слайд 4)
Учитель: Перед вами древняя карта Вавилона , и карта 1482 года . Изображение нечеткое, непонятное для чтения и определения реальных размеров.
Чтобы план местности был более точным, необходимо все его детали уменьшать в одно и тоже число раз с сохранением всех пропорций. Примером служат карты. (Слайд 5)
На карте участки земной поверхности изображаются в уменьшенном виде. Например, отрезок в 1 см на карте – это 1 м на местности. Найдем отношение длин отрезков. 1м = 100 см, значит 1:100, будет говорить о том, что 1 см изображения соответствует 100 см реального объекта (обращается внимание учащихся на обязательное совпадение единиц измерения)
Мы нашли отношение длины отрезка на карте к длине соответствующего расстояния на местности и эту величину называем масштабом, обозначение масштаба М 1:100
Отношение длины отрезка на карте к длине соответствующего отрезка на местности называют масштабом. (прочитаем определение в учебнике)(работа с учебником)
масштаб =
Давайте научимся определять масштаб
Задача: Найти масштаб плана, если длина отрезка на плане равна 4 см, а его длина на местности равна 200 м.
Выясняем, что нужно для нахождения масштаба найти отношение величин, для этого требуется выразить в одинаковых единицах измерения: 200м = 20 000 см.
Составляем отношение 4 : 20 000 = 

В чем обычно измеряется расстояние на местности? (в метрах и в километрах)
Выясняем в ходе беседы, что на карте расстояния измеряются в сантиметрах, а на местности в километрах. Возникает необходимость быстрого перевода сантиметров в километры и наоборот. Выявляем быстрый способ перевода, используя опорные схемы: (Приложение 2, рис 1)
| На карте | 1 см |
| На местности | 1 км = 100000 см |
| Масштаб | 1 : 100000 |
Если длина отрезка на карте 5 см, какова длина отрезка на местности для такого масштаба? (5∙100000 = 500000 см = 5 км)
Вопрос: Ребята, как вы думаете, в жизни приходится использовать только уменьшение для создания различных видов изображений реальных объектов? (Мы не можем нарисовать на альбомном листе человека того роста, который он имеет, нам необходимо уменьшить реальный объект для его изображения, что вы и делаете на уроках ИЗО; а если мы захотим нарисовать божью коровку или муравья, то нам придется на рисунке увеличить их размеры относительно реальных.)(Слайд 6-10)Посмотрите на модели машин, фотографии микроорганизмов, модель атома . Эти модели меньше чем в реальности, значит, чтобы получить реальные размеры этих предметов необходимо увеличить размеры моделей. (Слайд 11)Прочтите, пожалуйста, записи и объясните их смысл М 1:1000, М 1:4, М 2:1, М 4:1
Какие из записанных масштабов можно применять для увеличения, а какие для уменьшения? Почему вы так думаете?
Дети высказывают мнения, далее делается общий вывод:
Если в записи масштаба вторая величина больше первой, то данный масштаб дает уменьшение реальных размеров и наоборот.
Обобщим понятие масштаба. (Слайд 12)
Отношение длины отрезка на изображении к длине соответствующего отрезка на реальном объекте называют масштабом.
Масштаб показывает, во сколько раз расстояние на изображении меньше или больше, чем расстояние на реальном объекте.
5. Физкульминутка
6. Первичное осмысление и применение изученного
Учитель: емецкий поэт, государственный деятель, мыслитель И. Гете сказал:–«Мало знать, надо и применять, мало хотеть, надо и делать». (Слайд 13)
Мы вспомнили понятие масштаба из курса географии, сформулировали понятие масштаба в математике, а теперь, попробуем вместе с вами показать важность темы «Масштаб», показать его применение в жизни. Убедимся в использовании масштаба не только в географии и математике, но и в физике, химии, истории и др.
Задача 1 (Решаем вместе с классом, обсуждаем этапы решения задачи. Записываем решение на доске и в тетрадях.)Найти длину соответствующего отрезка на местности (Слайд 14)
Обсудим решение задачи и запишем в тетради.
Масштаб плана местности 1:1000000.
Что означает данная запись? (1 см на плане – 1000000 см на местности).
Составим схему решения.
| Отрезок | Масштаб | |
| Карта | 3 см | 1 |
| Местность | х | 1000000 |
Запишем пропорцию и решим ее.
х = 1000000·3:1 = 3000000 см = 30 км
7. Применение знаний и способов действий
Попробуйте отгадать загадку: «Земля есть – копать нельзя! Дороги есть – ехать нельзя! Реки есть – плыть нельзя!».
Как Вы думаете, о чём пойдёт речь? (о географической карте).
Географическая карта – один из важнейших документов человеческой культуры. Большие территории, изображаются на географических картах. Перед вами карта Курской области.
(Индивидуальная работа)(Приложение 3)
Задача 2: Рейсовый автобус движется по маршруту Обоянь – Курск. Сколько времени будет находиться автобус в пути,если его средняя скорость 50 км/ч?(Слайд 15)
Вопросы: Как найти время? (Надо путь разделить на скорость)
Все ли данные есть в условии задачи? (Нет, мы не знаем расстояние от Обояни до Курска)
Где взять недостающие данные? (Определить по карте)
Решение задачи выполняют самостоятельно, комментируя решение.
- Найдем расстояние от Обояни до Курска по карте (6,5 см)
- Зная масштаб 1:1000000 (в 1 см – 10 км), найдем расстояние на местности
| На карте | 6,5 | 1 |
| На местности | х | 1600000 |
Х = 6,5∙1000000 = 6500000 м = 65 км
- По формуле пути найдем время t=s/v.
Прослушать несколько ответов. Вопрос: Как вы думаете, при решении задачи получаются точные ответы? (могут быть различия при измерении расстояния) Вопрос: Точным ли будет время, найденное вами? Почему? (неточное, потому, что путь по карте находится по прямой, а дорога не является прямой линией)
Задача 3: По местам боевых действий (Работа в парах.)(Приложение 3) В прошлом году вся страна и в том числе Курская и Белгородская области праздновали 70-летие победы в Курской битве.12 июля 1943 г. под небольшим селом Прохоровка произошло крупнейшее танковое сражение второй мировой войны. Перед вами карта боевых действий, обстановка перед Курской битвой к исходу 4 июля 1943 года. Задание: Определите протяженность линии фронта от Белгорода до Орла.
План решения обсуждаем с детьми.
- Как изображена линия фронта?(кривая линия)
- Можно ли линейкой измерить эту линию?(нет)
- Чем, из имеющихся у вас на столе инструментов или подручных средств можно измерить линию фронта? Как это сделать?(ниткой, а потом длину найти по линейке)
- Измерим расстояние от Белгорода до Орла на карте (15,5 см)
- Зная масштаб карты, найдем расстояние на местности
| на карте | 15,5 | 1 |
| На местности | х | 3000000 |
х= 15,5∙3000000 = 46500000 м = 465 км
Рассмотрим примеры применения масштаба в жизни. (Работаем в группах.)(Приложение 3)
Каждой группе надо выполнить практическое задание. Вы решили в квартире сделать ремонт полов. Покрыть полы можно линолеумом, паркетом, кафелем. Сколько средств вы должны вложить в ремонт в каждом случае. (Каждая группа производит расчеты для одного вида покрытия).
Задача 4: Ремонт квартиры Решаем задачу в группах. Одна группа рассчитывает стоимость полов в 1 комнате, если их застелить линолеумом, другая группа – паркетом, третья рассчитывает стоимость полов 2 комнаты, если их застелить ковролином, и 4 группа –линолеумом. После того когда задача будет решена, один человек из группы должен рассказать классу решение. (Слайд 17)
Вычислите площадь квартиры, если сторона одной клетки плана равна 1см.
Ответ дайте в м² . Посчитайте во сколько вам обойдется ремонт каждой комнаты, если Линолеум – 400 р. за кв.м.Кафель – 200 р. за кв.м.Паркет – 600 р. за кв.м.
| 1 группа | |
| а = 3 см на плане, | 3∙100 = 300 см = 3 м в реальности |
| b = 4 см на плане, | 4∙100 = 400 см = 4 м в реальности |
| S=a∙b, | S= 3∙4 = 12м ² |
| 12∙400 = 4800 (руб) стоимость линолеума | |
| 2 группа | |
| a= 2 см на плане. | 2∙100 = 200 см = 2 м в реальности |
| в= 4 см на плане, | 4∙100 = 400 см = 4 м в реальности |
| S=a∙b. S= 2∙4 = 8 м² | 200∙8 = 1600 (руб) стоимость кафеля |
| 3 группа | |
| a =3 см на плане | 3∙100 = 300 см = 3 м в реальности |
| b =4 см на плане | 4∙100 = 400 см = 4 м в реальности |
| S=a∙b. S = 3∙4 = 12 м² | 600∙12 = 7200 (руб) стоимость паркета |
| 1600+4800+7200 = 13600 (руб) стоимость ремонта полов | |
Ответ: 13600 рублей
Задача 5: Пешеход, двигаясь равномерно и прямолинейно, отметил моменты прохождения им пункта А и В. Определите скорость движения пешехода в м/мин (Слайд 18)
- Как вычислить скорость? (Путь разделить на время).
- Какие данные можно определить по рисунку? (времяна часах).
- Как определить путь? (измерить линейкой расстояние от А до В и зная масштаб вычислить реальное расстояние)
Решение: t = 20 мин, s= 15 см – на плане, 1500 м – на местности. Найдем скорость v = 1500:20 = 75 м/мин
8. Подведение итогов урока
Учитель: Вернемся к теме нашего урока. Чему нас научил этот урок и что мы на нем узнали? (Ответы детей). Да, самое главное, что показал этот урок, что математика необходима нам в жизни. Задачи ставятся разные, но при решении многих задач математика просто необходима. В частности масштаб.
Ребята, подведем итоги урока. (Слайд 19)
Я предлагаю вам закончить предложения:
- Я знаю, что масштаб – это ….
- я научился…
- у меня получилось …
- теперь я могу…
Как вы считаете, мы достигли целей урока? Тема масштаб применима в жизни?
А теперь я хотела бы вернуться к началу урока и услышать ответ на вопрос. Можно ли объять необъятное и увидеть невидимое?
Вы все хорошо поработали, но особенно мне хотелось бы отметить .
(учитель выставляет мотивированную оценку)
9. Домашнее задание
- № 841(Дополнительно) Во сколько обойдётся ремонт полов в комнате, если использовать ковролин по 500 руб. за м2.
- № 843
10. Рефлексия
Ребята, благодарю вас за активную работу на протяжении всего урока.
Мне бы хотелось узнать, с каким настроением каждый из вас закончил этот урок.
Каждое урок – это новые знания, достижение цели, а значит маленькие победы. Определите себе место на нашем пьедестале. У вас на столах лежат смайлики. Возьмите смайлик, который соответствует вашему настроению, и прикрепите на наш символический олимпийский пьедестал. (Приложение 2, рис 2)
1 место – я все понимаю, могу решать задачи.
2 место – я все понимаю, но имею некоторые затруднения в решении задач.
3 место – я почти все понимаю, но задачи решаю только не очень сложные.
Спасибо за урок. До свидания! (Слайд 21)
💥 Видео
Масштаб карты. География 5 классСкачать

Высоты треугольника.Скачать

Сумма углов треугольника. Геометрия 7 класс | МатематикаСкачать

Определение натуральной величины треугольника АВС методом замены плоскостей проекцииСкачать

По силам каждому ★ Найдите стороны треугольника на рисункеСкачать

Теорема ПИФАГОРА ❤️Скачать

ЧТО НАДО ГОВОРИТЬ ЕСЛИ НЕ СДЕЛАЛ ДОМАШКУ!Скачать