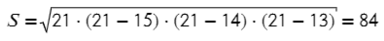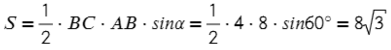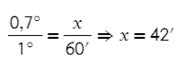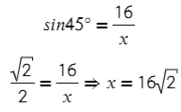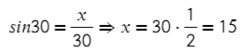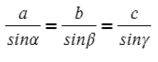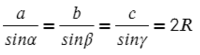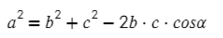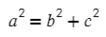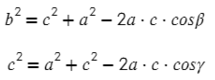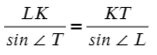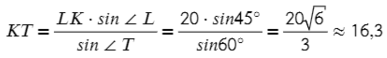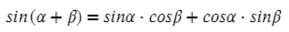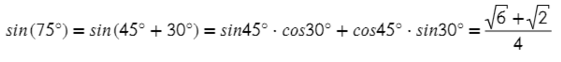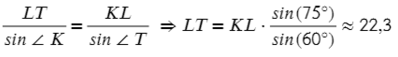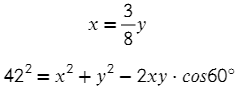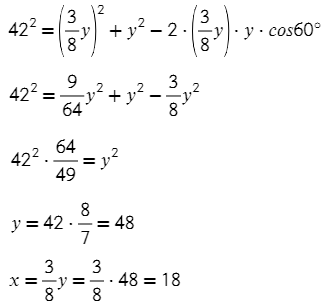Как найти икс у треугольника (7 видео) | Курс школьной геометрии

Решение треугольников онлайн

С помощю этого онлайн калькулятора можно решить треугольники, т.е. найти неизвестные элементы (стороны, углы) треугольника. Теоретическую часть и численные примеры смотрите ниже.

Решение треугольников − это нахождение всех его элементов (трех сторон и трех углов) по трем известным элементам (сторонам и углам). В статье Треугольники. Признаки равенства треугольников рассматриваются условия, при которых два треугольника оказываются равными друг друга. Как следует из статьи, треугольник однозначно определяется тремя элементами. Это:

Три стороны треугольника.
Две стороны треугольника и угол между ними.
Две стороны и угол противостоящий к одному из этих сторон треугольника.
Одна сторона и любые два угла.

Заметим, что если у треугольника известны два угла, то легко найти третий угол, т.к. сумма всех углов треугольника равна 180°.

Содержание

Решение треугольника по трем сторонам
Решение треугольника по двум сторонам и углу между ними
Решение треугольника по стороне и любым двум углам
Теория и практика по треугольникам (Часть Ⅱ)
Площадь произвольного треугольника
Тригонометрия в прямоугольных треугольниках
Теорема синусов и теорема косинусов
Что нужно знать:
Как найти стороны прямоугольного треугольника
Онлайн калькулятор
Найти гипотенузу (c)
Найти гипотенузу по двум катетам
Найти гипотенузу по катету и прилежащему к нему острому углу
Найти гипотенузу по катету и противолежащему к нему острому углу
Найти гипотенузу по двум углам
Найти катет
Найти катет по гипотенузе и катету
Найти катет по гипотенузе и прилежащему к нему острому углу
Найти катет по гипотенузе и противолежащему к нему острому углу
Найти катет по второму катету и прилежащему к нему острому углу
Найти катет по второму катету и противолежащему к нему острому углу
💡 Видео

Видео:Найдите сторону треугольника на рисункеСкачать

Решение треугольника по трем сторонам

Пусть известны три стороны треугольника a, b, c (Рис.1). Найдем .

(1)

(2)

Из (1) и (2) находим cosA, cosB и углы A и B (используя калькулятор). Далее, угол C находим из выражения

Пример 1. Известны стороны треугольника ABC: Найти (Рис.1).

Решение. Из формул (1) и (2) находим:

И, наконец, находим угол C:

Видео:Найдите третью сторону треугольникаСкачать

Решение треугольника по двум сторонам и углу между ними

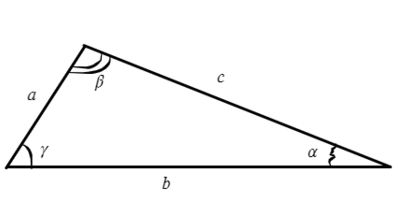
Пусть известны стороны треугольника a и b и угол между ними C (Рис.2). Найдем сторону c и углы A и B.

Найдем сторону c используя теорему косинусов:

Далее, из формулы

(3)

Далее из (3) с помощью калькулятора находим угол A.

Поскольку уже нам известны два угла то находим третий:

Пример 2. Известны две стороны треугольника ABC: и (Рис.2). Найти сторону c и углы A и B.

Решение. Иcпользуя теорму косинусов найдем сторону c:

Из формулы (3) найдем cosA:

Поскольку уже нам известны два угла то находим третий:

Видео:Уравнения стороны треугольника и медианыСкачать

Решение треугольника по стороне и любым двум углам

Пусть известна сторона треугольника a и углы A и B (Рис.4). Найдем стороны b и c и угол C.

Так как, уже известны два угла, то можно найти третий:

Далее, для находждения сторон b и c воспользуемся тероемой синусов:

Пример 3. Известна одна сторона треугольника ABC: и углы (Рис.3). Найти стороны b и c и угол С.

Решение. Поскольку известны два угла, то легко можно найти третий угол С:

Найдем сторону b. Из теоремы синусов имеем:

Найдем сторону с. Из теоремы синусов имеем:

Видео:Найдите сторону треугольника, если другие его стороны равны 1 и 5Скачать

Теория и практика по треугольникам (Часть Ⅱ)

Площадь треугольников.

Тригонометрия в прямоугольных треугольниках.

Что такое синус/косинус.

Таблицы Брадиса. Как пользоваться.

Теорема синусов и косинусов.

Геометрия — это искусство хорошо рассуждать на плохо выполненных чертежах.

С основными свойствами разобрались, теперь рассмотрим формулы и их приминение.

Площадь произвольного треугольника

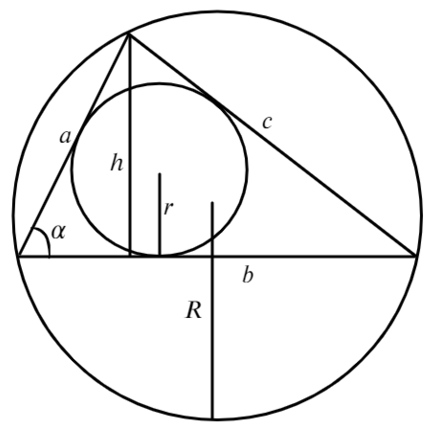
Нет, это не кривая пентаграмма, нужны на этом рисунке только обозначения. Рассмотрим формулы школьной программы.

Высоту умножаем на ту сторону, на которую приходит высота:
В эту формулу подставляем угол между сторонами a и b:

Удобно использовать эту формулу, когда известны все стороны треугольника, p — полупериметр (половина суммы длин всех сторон):

Данная формула отлично помогает найти радиус вписанной окружности для любого треугольника, если известна площадь:

А эта формула помогает найти радиус описанной окружности для любого треугольника:

А зачем такое количество формул? К каждой задаче будут предоставлять разное дано, удобно знать и применять все формулы, чтобы максимально быстро решать задачи.

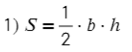
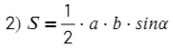
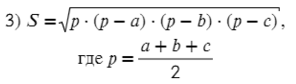
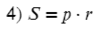
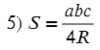
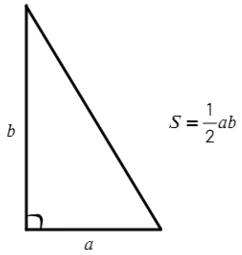
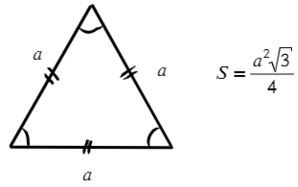
Полезные формулы для прямоугольного и равностороннего треугольника:

В данном случае получается, что один катет «b» — высота треугольника, а катет «а» — основание.

Эту формулу можно вывести большим количеством способов, самый простой через формулу №2

Задача №1. Дано на рисунке:

Оттолкнемся от вопроса: нужно найти площадь. Помимо 5 формул для произвольного треугольника, нам подойдет формула нахождения площади через полупроизведение катетов.

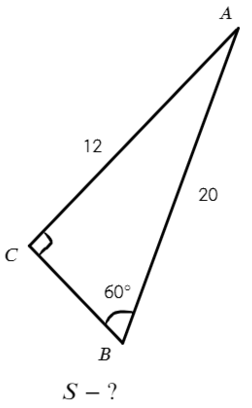
Вариантов здесь много (можно через т. Пифагора), но самый быстрый — найти ∠А = 180°− 90° − 60° = 30°, тогда площадь найдем по (2) формуле: S = ½absinα

Ответ: 60

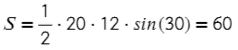
Задача №2. Дано на рисунке:

Снова оттолкнемся от вопроса: нужно найти площадь. Дан обычный треугольник, значит, наш выбор ограничен первыми 5−ью формулами. В первой нужна высота, во второй угол, а в третьей полупериметр, но мы же знаем все стороны! Для начала найдем периметр и полупериметр:

Теперь можно подставить все числа в формулу площади:

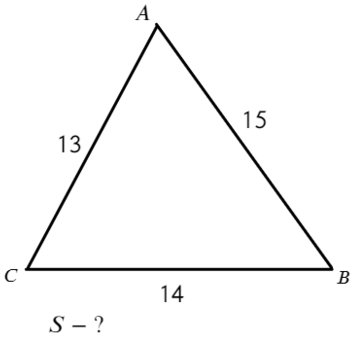
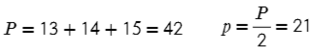
Главное — правильно определиться с формулой.

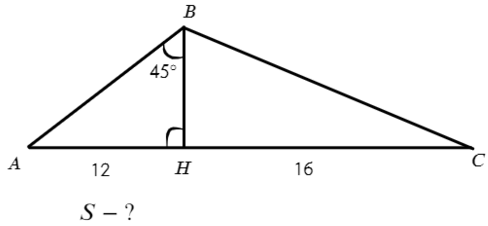
Задача №3. Дано на рисунке:

В ΔABH: ∠A = 180°− 90° − 45° = 45°, значит, ∠A = ∠B => BH = AH = 12.

Тогда площадь можно найти по формуле (1) S=½bh. Высота AH = 12, основание AC = 16+12 = 28. => S = ½×12×28 = 168

Задача №4. Дано на рисунке:

Оттолкнемся от отношения, которое нам дано. Мы знаем, что сумма данных углов равна 90°, если ∠ACM = х и ∠ВCM = 2х, тогда 2х+х = 90°

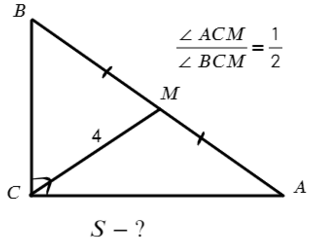
∠ACM = х = 30° => ∠ВCM = 60°. А что у нас равно 4-ем? Да, медиана! А медиана, проведенная из прямого угла, равна половине гипотенузы (2−ое свойство). Тогда отметим равные углы:

В ΔBCM получается ∠ВCM = ∠СВM = 60°, тогда ∠СМВ = 60° и ΔBCM — правильный:

Площадь найдем по (2) формуле: S = ½absinα:

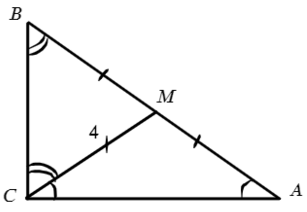
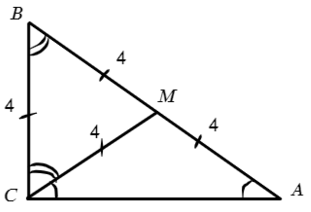
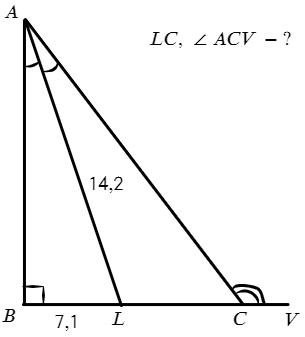
Задача №5. Дано на рисунке:

В дано есть только стороны, а найти нужно угол. Как это сделать? Вот стороны 14,2 и 7,1 во сколько раз отличаются? Да, в 2 раза, а значит угол ∠BAL = 30° (против угла в 30° лежит катет, который в два раза меньше гипотенузы).

Значит, ∠A = 60° => ∠ACB = 180° − 90° − 60° = 30°, а ∠ACB — смежный с ∠ACV => ∠ACV = 180° − 30° = 150°.

Что касается LC: внимательно рассмотрим ΔALC, можно даже лупой воспользоваться. Что видишь? ∠LAC = ∠ACL = 30° => ΔALC — равнобедренный, LC = AL = 14,2.

Ответ: 14,2 и 150°

Тригонометрия в прямоугольных треугольниках

В прямоугольном треугольнике три стороны: 2 катета и гипотенуза.

Катеты меньшие стороны треугольника. Гипотенуза большая сторона, которая лежит напротив угла в 90°.

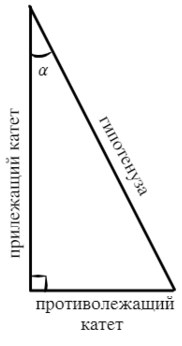
Относительно угла α:

Катет, который составляет угол, называют прилежащим. Катет, который находится напротив угла, называют противолежащим. Логично? Замечательно!

Тригонометрические функции (синус, косинус. ) задают связь между углом и длинами сторон.

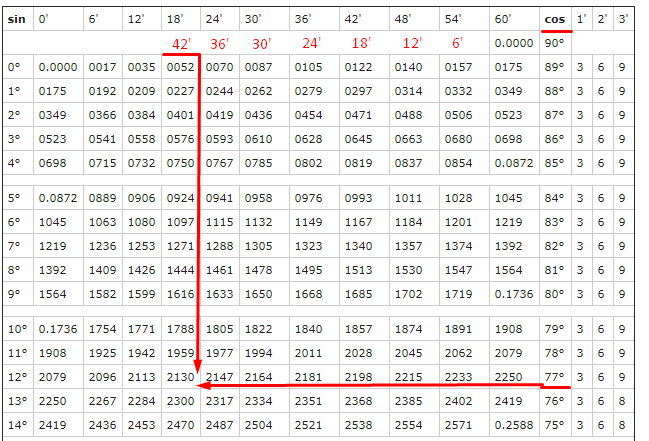
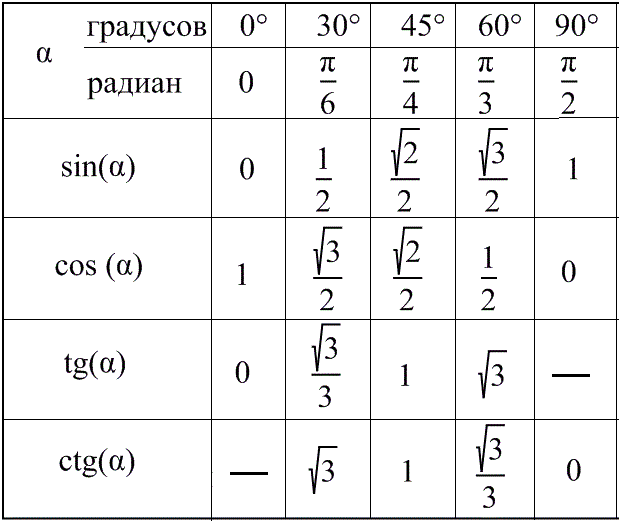
Но хорошо бы знать какие-то значения тригонометрических функций при определенных углах. Все значения вместе образуют таблицу Брадиса. С ее помощью можно вычислить почти любое значение тригонометрической функции при заданом угле. Но как с ней работать?

Найдем sin(10°) . Для этого выберем столбец sin и в нем найдем 10°. Ближайшее значение — это то, что нам нужно — 0,1736.

А что за столбец 0′; 6′; 12′ и т.д. Это минуты! Не те, которых мы ждем в конце урока, а градусные минуты.

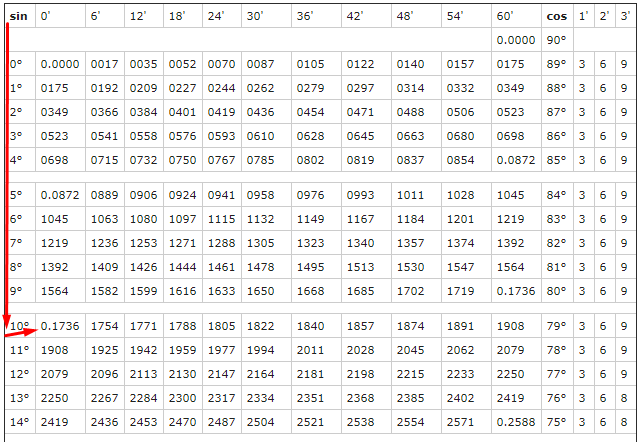
Из общего: и те, и другие минуты измеряются в промежутке от 0 до 60.

Градусные минуты делят один градус на 60 минут (1°=60′), нужны они для большей точности задания угла.

p.s. Есть еще и градусные секунды, и в одной градусной минуте 60 градусных секунд, знакомо? 1° = 60′ = 3600».

Семь десятых градуса нужно перевести в минуты. Можно через пропорцию:

Теперь в таблице нужно найти 77°42′ для косинуса. Для синуса минуты прописаны, а для косинуса нет. Но мы же люди не гордые, сами напишем, но в обратном порядке. На пересечении 77° и 42′ получаем наше значение:

Но чтобы не загромождать таблицу 0, его в начале пишут только в первых строчках, поэтому ответ cos(77,7°) = 0,213.

В задачах же таким обилием углов похвастаться нельзя, достаточно знать значения для 30°; 45°; 60°; 90°.

Искусство решать геометрические задачи чем-то напоминает трюки иллюзионистов — иногда,

даже зная решение задачи, трудно понять, как можно было до него додуматься.

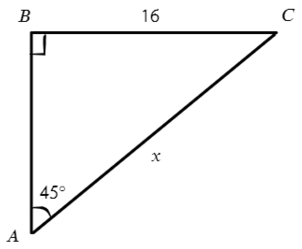
Задача №6. Дано на рисунке:

В этой задаче известен противолежащий катет относительно угла в 45°, а найти нужно гипотенузу. Смотрим, где у нас есть противполежащий катет и гипотенуза? Это синус!

Смотрим в таблице, чему равен синус 45°, и подставляем в отношение:

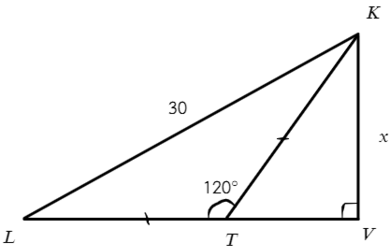
Задача №7. Дано на рисунке:

Мы разобрались с тригонометрическими функциями в прямоугольных треугольниках, значит, и в этой задаче нужно перейти к прямоугольному треугольнику.

В ΔLTK — равнобедренный : ∠L = ∠LKT = (180° − 120°)/2 = 30°

Отлично, в прямоугольном ΔLVK: ∠L = 30° и известна гипотенуза, а нам нужно найти противолежащий катет, чем воспользуемся? Опять синусом!

Теорема синусов и теорема косинусов

Сразу возникает вопрос, а теорема тангенсов тоже есть? Конечно, есть, но она очень редко используется.

Для любого треугольника можно записать такое соотношение, это будет теорема синусов:

Запомни, что сторона относится к синусу противолежащего угла.

Следствие из теорма синусов гласит, что любое соотношение равно двум радиусам описанной окружности:

Для любого треугольника можно записать такое соотношение, это будет теорема косинусов:

А что будет, если α = 90°, а cos(90) = 0? Получится:

Теорема Пифагора, вот так просто можно запомнить теорему косинусов. Начать как теорему Пифагора, а затем вычесть удвоенное произведение на косинус угла между ними.

Можно записать и для других сторон в этом же треугольнике:

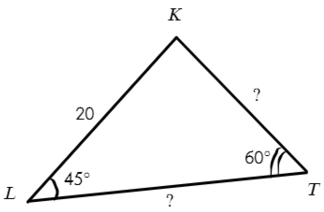
Задача №8. Дано на рисунке:

Запишем теорему синусов для двух отношений:

Выразим отсюда KT:

∠K = 180° − 60° − 45° = 75°. Чтобы найти синус угла 75°, советую посмотреть эту статью, нужно воспользовать формулой суммы синусов:

Тогда представим 75° в виде двух табличных значений:

Аналогично выразим LT:

Ответ: 16,3 и 22,3

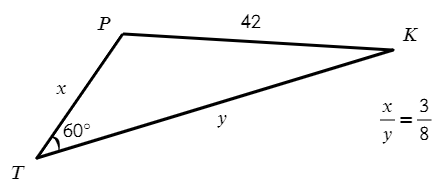
Задача №9. Дано на рисунке:

Найти нужно x и y. Запишем теорему косинусов для этого треугольника:

Икс выразим через игрек:

Отлично, поздравляю тебя с Elementary по геометрии!

Что нужно знать:

Вертикальные, смежные, соответственные, накрест лежащие углы.
Равенство и подобие треугольников.
Что такое медиана, биссектриса, высота.
Свойства треугольников.
Площадь треугольников.
Синус/косинус в треугольнике.
Теорему синусов и косинусов.

Видео:ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

Как найти стороны прямоугольного треугольника

Видео:По силам каждому ★ Найдите стороны треугольника на рисункеСкачать

Онлайн калькулятор

Чтобы вычислить длины сторон прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):

для гипотенузы (с):
- длины катетов a и b
- длину катета (a или b) и прилежащий к нему острый угол (β или α, соответственно)
- длину катета (a или b) и противолежащий к нему острый угол (α или β, соответственно)
для катета:
- длину гипотенузы (с) и длину одного из катетов
- длину гипотенузы (с) и прилежащий к искомому катету (a или b) острый угол (β или α, соответственно)
- длину гипотенузы (с) и противолежащий к искомому катету (a или b) острый угол (α или β, соответственно)
- длину одного из катетов (a или b) и прилежащий к нему острый угол (β или α, соответственно)
- длину одного из катетов (a или b) и противолежащий к нему острый угол (α или β, соответственно)