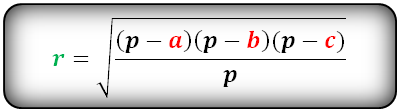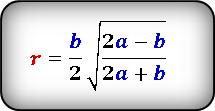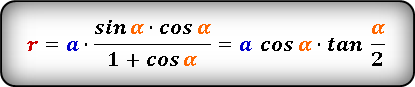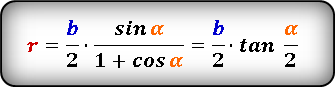- Определение
- Формулы
- Радиус вписанной окружности в треугольник
- Радиус описанной окружности около треугольника
- Площадь треугольника
- Периметр треугольника
- Сторона треугольника
- Средняя линия треугольника
- Высота треугольника
- Свойства
- Доказательство
- Все формулы для радиуса вписанной окружности
- Радиус вписанной окружности в треугольник
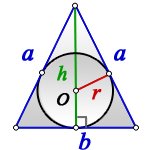
- Радиус вписанной окружности в равносторонний треугольник
- Радиус вписанной окружности равнобедренный треугольник
- Как найти диаметр окружности
- Основные понятия
- Как узнать диаметр. Формулы
- 1. Общая формула.
- 2. Если перед нами стоит задача найти диаметр по длине окружности
- 3. Если есть чертеж окружности
- 📽️ Видео
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Определение
Треугольник, вписанный в окружность — это треугольник, который
находится внутри окружности и соприкасается с ней всеми тремя вершинами.
На рисунке 1 изображена окружность, описанная около
треугольника и окружность, вписанная в треугольник.
ВD = FC = AE — диаметры описанной около треугольника окружности.
O — центр вписанной в треугольник окружности.
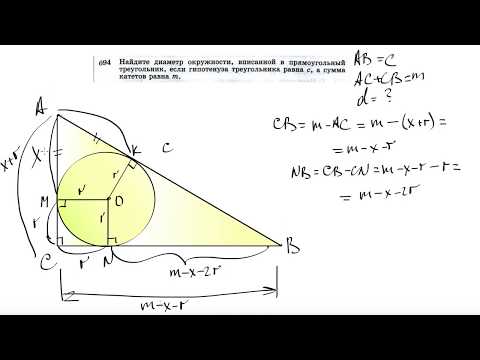
Видео:№694. Найдите диаметр окружности, вписанной в прямоугольный треугольник, если гипотенузаСкачать
Формулы
Радиус вписанной окружности в треугольник
r — радиус вписанной окружности.
- Радиус вписанной окружности в треугольник,
если известна площадь и все стороны:
Радиус вписанной окружности в треугольник,
если известны площадь и периметр:
Радиус вписанной окружности в треугольник,
если известны полупериметр и все стороны:
Радиус описанной окружности около треугольника
R — радиус описанной окружности.
- Радиус описанной окружности около треугольника,
если известна одна из сторон и синус противолежащего стороне угла:
Радиус описанной окружности около треугольника,
если известны все стороны и площадь:
Радиус описанной окружности около треугольника,
если известны все стороны и полупериметр:
Площадь треугольника
S — площадь треугольника.
- Площадь треугольника вписанного в окружность,
если известен полупериметр и радиус вписанной окружности:
Площадь треугольника вписанного в окружность,
если известен полупериметр:
Площадь треугольника вписанного в окружность,
если известен высота и основание:
Площадь треугольника вписанного в окружность,
если известна сторона и два прилежащих к ней угла:
Площадь треугольника вписанного в окружность,
если известны две стороны и синус угла между ними:
[ S = fracab cdot sin angle C ]
Периметр треугольника
P — периметр треугольника.
- Периметр треугольника вписанного в окружность,
если известны все стороны:
Периметр треугольника вписанного в окружность,
если известна площадь и радиус вписанной окружности:
Периметр треугольника вписанного в окружность,
если известны две стороны и угол между ними:
Сторона треугольника
a — сторона треугольника.
- Сторона треугольника вписанного в окружность,
если известны две стороны и косинус угла между ними:
Сторона треугольника вписанного в
окружность, если известна сторона и два угла:
Средняя линия треугольника
l — средняя линия треугольника.
- Средняя линия треугольника вписанного
в окружность, если известно основание:
Средняя линия треугольника вписанного в окружность,
если известныдве стороны, ни одна из них не является
основанием, и косинус угламежду ними:
Высота треугольника
h — высота треугольника.
- Высота треугольника вписанного в окружность,
если известна площадь и основание:
Высота треугольника вписанного в окружность,
если известен сторона и синус угла прилежащего
к этой стороне, и находящегося напротив высоты:
[ h = b cdot sin alpha ]
Высота треугольника вписанного в окружность,
если известен радиус описанной окружности и
две стороны, ни одна из которых не является основанием:
Видео:Окружность вписана в равносторонний треугольник, найти радиусСкачать

Свойства
- Центр вписанной в треугольник окружности
находится на пересечении биссектрис. - В треугольник, вписанный в окружность,
можно вписать окружность, причем только одну. - Для треугольника, вписанного в окружность,
справедлива Теорема Синусов, Теорема Косинусов
и Теорема Пифагора. - Центр описанной около треугольника окружности
находится на пересечении серединных перпендикуляров. - Все вершины треугольника, вписанного
в окружность, лежат на окружности. - Сумма всех углов треугольника — 180 градусов.
- Площадь треугольника вокруг которого описана окружность, и
треугольника, в который вписана окружность, можно найти по
формуле Герона.
Видео:Как найти диаметр окружности, описанной около равнобедренного треугольникаСкачать

Доказательство
Около любого треугольника, можно
описать окружность притом только одну.
окружность и треугольник,
которые изображены на рисунке 2.
окружность описана
около треугольника.
- Проведем серединные
перпендикуляры — HO, FO, EO. - O — точка пересечения серединных
перпендикуляров равноудалена от
всех вершин треугольника. - Центр окружности — точка пересечения
серединных перпендикуляров — около
треугольника описана окружность — O,
от центра окружности к вершинам можно
провести равные отрезки — радиусы — OB, OA, OC.
окружность описана около треугольника,
что и требовалось доказать.
Подводя итог, можно сказать, что треугольник,
вписанный в окружность — это треугольник,
в котором все серединные перпендикуляры
пересекаются в одной точке, и эта точка
равноудалена от всех вершин треугольника.
Видео:Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать

Все формулы для радиуса вписанной окружности
Видео:КАК НАЙТИ ДИАМЕТР ОКРУЖНОСТИ, ЕСЛИ ИЗВЕСТНА ДЛИНА ОКРУЖНОСТИ? Примеры | МАТЕМАТИКА 6 классСкачать

Радиус вписанной окружности в треугольник
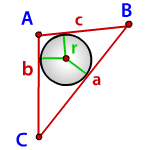
a , b , c — стороны треугольника
p — полупериметр, p=( a + b + c )/2
Формула радиуса вписанной окружности в треугольник ( r ):
Видео:Радиус описанной окружностиСкачать

Радиус вписанной окружности в равносторонний треугольник
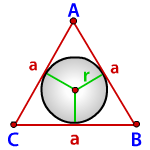
a — сторона треугольника
r — радиус вписанной окружности
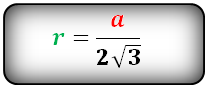
Формула для радиуса вписанной окружности в равносторонний треугольник ( r ):
Видео:Геометрия 9 класс. Радиус описанной и вписанной окружности треугольника. Формулы радиуса.Скачать

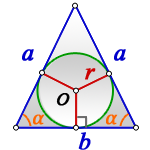
Радиус вписанной окружности равнобедренный треугольник
1. Формулы радиуса вписанной окружности если известны: стороны и угол
a — равные стороны равнобедренного треугольника
b — сторона ( основание)
α — угол при основании
О — центр вписанной окружности
r — радиус вписанной окружности
Формула радиуса вписанной окружности в равнобедренный треугольник через стороны ( r ) :
Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и угол ( r ) :
2. Формулы радиуса вписанной окружности если известны: сторона и высота
a — равные стороны равнобедренного треугольника
b — сторона ( основание)
h — высота
О — центр вписанной окружности
r — радиус вписанной окружности
Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и высоту ( r ) :
Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Как найти диаметр окружности
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Видео:Длина окружности. Площадь круга. 6 класс.Скачать

Основные понятия
Прежде чем погружаться в последовательность расчетов, важно понять разницу между понятиями.
Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра, которая лежит в той же плоскости.
Круг — часть плоскости, лежащая внутри окружности, а также сама окружность.
Если говорить проще, окружность — это замкнутая линия, как, например, обруч и велосипедное колесо. Круг — часть плоскости, ограниченная окружностью, как блинчик или вырезанный из картона кружок.
Диаметр — отрезок, который соединяет две точки окружности и проходит через ее центр.
Радиус — отрезок, который соединяет центр окружности и любую точку на ней.
Видео:Длина окружности. Математика 6 класс.Скачать

Как узнать диаметр. Формулы
В данной теме нам предстоит узнать три формулы:
1. Общая формула.
Исходя из основных определений нам известно, что значение диаметра равно двум радиусам: D = 2 × R, где D — диаметр, R — радиус.
2. Если перед нами стоит задача найти диаметр по длине окружности
D = C : π, где C — длина окружности, π — это константа, которая равна отношению длины окружности к диаметру, она всегда равна 3,14.
Чтобы получить правильный ответ, можно поделить столбиком или использовать онлайн-калькулятор.
3. Если есть чертеж окружности
- Начертить внутри круга прямую горизонтальную линию. Ее месторасположение не играет значительной роли.
- Отметить точки пересечения прямой и окружности.
- Начертить при помощи циркуля две окружности одного радиуса (больше, чем радиус первоначальной окружности), первую — с центром в точке A, вторую — с центром в точке B.
- Провести прямую через две точки, в которых произошло пересечение. Отметить точки пересечения полученной прямой с окружностью. Диаметр равен этому отрезку.
- Теперь осталось измерить диаметр круга при помощи линейки. Получилось!
Эти простые формулы могут пригодиться не только на школьных уроках, но и если вы решите освоить профессию дизайнера интерьера, архитектора или модельера одежды.
📽️ Видео
найти радиус окружности, описанной вокруг треугольникаСкачать

Вписанные и описанные окружности. Вебинар | МатематикаСкачать

№702. В окружность вписан треугольник ABC так, что АВ — диаметр окружности. Найдите углыСкачать

Сможешь найти радиус окружности? Окружность, вписанная в прямоугольный треугольникСкачать

Вписанная и описанная окружность - от bezbotvyСкачать

Треугольник и окружность #shortsСкачать

Окружность, диаметр, хорда геометрия 7 классСкачать

Формулы для радиуса окружности #shortsСкачать

Вписанный в окружность прямоугольный треугольник.Скачать