С помощю этого онлайн калькулятора можно решить треугольники, т.е. найти неизвестные элементы (стороны, углы) треугольника. Теоретическую часть и численные примеры смотрите ниже.
Решение треугольников − это нахождение всех его элементов (трех сторон и трех углов) по трем известным элементам (сторонам и углам). В статье Треугольники. Признаки равенства треугольников рассматриваются условия, при которых два треугольника оказываются равными друг друга. Как следует из статьи, треугольник однозначно определяется тремя элементами. Это:
- Три стороны треугольника.
- Две стороны треугольника и угол между ними.
- Две стороны и угол противостоящий к одному из этих сторон треугольника.
- Одна сторона и любые два угла.
Заметим, что если у треугольника известны два угла, то легко найти третий угол, т.к. сумма всех углов треугольника равна 180°.
- Решение треугольника по трем сторонам
- Решение треугольника по двум сторонам и углу между ними
- Решение треугольника по стороне и любым двум углам
- Свойства сторон и углов треугольника
- Все формулы для треугольника
- 1. Как найти неизвестную сторону треугольника
- 2. Как узнать сторону прямоугольного треугольника
- 3. Формулы сторон равнобедренного треугольника
- 4. Найти длину высоты треугольника
- 🌟 Видео
Видео:По силам каждому ★ Найдите стороны треугольника на рисункеСкачать

Решение треугольника по трем сторонам
Пусть известны три стороны треугольника a, b, c (Рис.1). Найдем 
 |
 |
 |
 | (1) |
 | (2) |
Из (1) и (2) находим cosA, cosB и углы A и B (используя калькулятор). Далее, угол C находим из выражения
 . . |
Пример 1. Известны стороны треугольника ABC: 

Решение. Из формул (1) и (2) находим:
  . . |
  . . |
 , ,  . . |
И, наконец, находим угол C:
  |
Видео:Найдите третью сторону треугольникаСкачать

Решение треугольника по двум сторонам и углу между ними
Пусть известны стороны треугольника a и b и угол между ними C (Рис.2). Найдем сторону c и углы A и B.
 |
Найдем сторону c используя теорему косинусов:
 . . |
 . . |
Далее, из формулы
 . . |
 . . | (3) |
Далее из (3) с помощью калькулятора находим угол A.
Поскольку уже нам известны два угла то находим третий:
 . . |
Пример 2. Известны две стороны треугольника ABC: 

Решение. Иcпользуя теорму косинусов найдем сторону c:
 , , |
   . . |
Из формулы (3) найдем cosA:
  |
 . . |
Поскольку уже нам известны два угла то находим третий:
  . . |
Видео:Найдите сторону треугольника на рисункеСкачать

Решение треугольника по стороне и любым двум углам
Пусть известна сторона треугольника a и углы A и B (Рис.4). Найдем стороны b и c и угол C.
 |
Так как, уже известны два угла, то можно найти третий:
 . . |
Далее, для находждения сторон b и c воспользуемся тероемой синусов:
 , ,  . . |
 , ,  . . |
Пример 3. Известна одна сторона треугольника ABC: 

Решение. Поскольку известны два угла, то легко можно найти третий угол С:
  |
Найдем сторону b. Из теоремы синусов имеем:
 |
 |
Найдем сторону с. Из теоремы синусов имеем:
Видео:Почти никто не решил ➜ Найдите сторону треугольникаСкачать

Свойства сторон и углов треугольника
| Фигура | Рисунок | Формулировка | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Треугольник |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Большая сторона треугольника |  | Против большей стороны треугольника лежит больший угол | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Больший угол треугольника | Против большего угла треугольника лежит большая сторона | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Меньшая сторона треугольника |  | Против меньшей стороны треугольника лежит меньший угол | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Меньший угол треугольника | Против меньшего угла треугольника лежит меньшая сторона | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Длины сторон треугольника |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Углы треугольника |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Внешний угол треугольника |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Больший угол треугольника |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Меньший угол треугольника |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Теорема косинусов |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Теорема синусов |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Треугольник | ||
 | ||
| Большая сторона треугольника | ||
 | Против большей стороны треугольника лежит больший угол | |
| Больший угол треугольника | ||
 | Против большего угла треугольника лежит большая сторона | |
| Меньшая сторона треугольника | ||
 | Против меньшей стороны треугольника лежит меньший угол | |
| Меньший угол треугольника | ||
 | Против меньшего угла треугольника лежит меньшая сторона | |
| Длины сторон треугольника | ||
 | ||
| Углы треугольника | ||
 | ||
| Внешний угол треугольника | ||
 | ||
| Больший угол треугольника | ||
 | ||
| Меньший угол треугольника | ||
 | ||
| Теорема косинусов | ||
 | ||
| Теорема синусов | ||
 | ||
| Треугольник |
 |
Рассматриваются три точки, не лежащие на одной прямой, и три отрезка, соединяющие эти точки.
Определение . Треугольником называют часть плоскости, ограниченную этими отрезками, отрезки называют сторонами треугольника , а концы отрезков – вершинами треугольника .

Свойство большей стороны треугольника:
Против большей стороны треугольника лежит больший угол

Свойство большего угла треугольника:
Против большего угла треугольника лежит большая сторона

Свойство меньшей стороны треугольника:
Против меньшей стороны треугольника лежит меньший угол

Свойство меньшего угла треугольника:
Против меньшего угла треугольника лежит меньшая сторона

Длины сторон треугольника удовлетворяют неравенству треугольника : длина любой стороны треугольника меньше суммы длин двух других сторон.
a неравенству треугольника : длина любой стороны треугольника больше модуля разности длин двух других сторон.

Свойство углов треугольника:
Сумма углов треугольника равна 180°
Свойство внешнего угла треугольника:
Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.

Свойство большего угла треугольника:
Величина большего угла треугольника не может быть меньшей, чем 60°.

где α – больший угол треугольника.

Свойство меньшего угла треугольника:
Величина меньшего угла треугольника не может быть большей, чем 60°.

где β – меньший угол треугольника.


Свойство меньшего угла треугольника:

Видео:Найдите сторону треугольника, если другие его стороны равны 1 и 5Скачать

Все формулы для треугольника
Видео:Нахождение стороны прямоугольного треугольникаСкачать

1. Как найти неизвестную сторону треугольника
Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.
a , b , c — стороны произвольного треугольника
α , β , γ — противоположные углы
Формула длины через две стороны и угол (по теореме косинусов), ( a ):
* Внимательно , при подстановке в формулу, для тупого угла ( α >90), cos α принимает отрицательное значение
Формула длины через сторону и два угла (по теореме синусов), ( a):
Видео:Найдите стороны треугольникаСкачать

2. Как узнать сторону прямоугольного треугольника
Есть следующие формулы для определения катета или гипотенузы
a , b — катеты
c — гипотенуза
α , β — острые углы
Формулы для катета, ( a ):
Формулы для катета, ( b ):
Формулы для гипотенузы, ( c ):
Формулы сторон по теореме Пифагора, ( a , b ):
Видео:Супер ЖЕСТЬ ➜ Найдите сторону треугольника ➜ Решить без тригонометрииСкачать

3. Формулы сторон равнобедренного треугольника
Вычислить длину неизвестной стороны через любые стороны и углы
b — сторона (основание)
a — равные стороны
α — углы при основании
β — угол образованный равными сторонами
Формулы длины стороны (основания), (b ):
Формулы длины равных сторон , (a):
Видео:Периметр треугольника. Как найти периметр треугольника?Скачать

4. Найти длину высоты треугольника
Высота— перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).
Высоты треугольника пересекаются в одной точке, которая называется — ортоцентр.

a — сторона, основание
b, c — стороны
β , γ — углы при основании
p — полупериметр, p=(a+b+c)/2
R — радиус описанной окружности
S — площадь треугольника
Формула длины высоты через стороны, ( H ):
Формула длины высоты через сторону и угол, ( H ):
Формула длины высоты через сторону и площадь, ( H ):
Формула длины высоты через стороны и радиус, ( H ):
🌟 Видео
Задача про стороны треугольника. Геометрия 7 класс.Скачать

Теорема косинусов. Решить задачи. Найти сторону по двум сторонам и углу. Найти угол по сторонам.Скачать

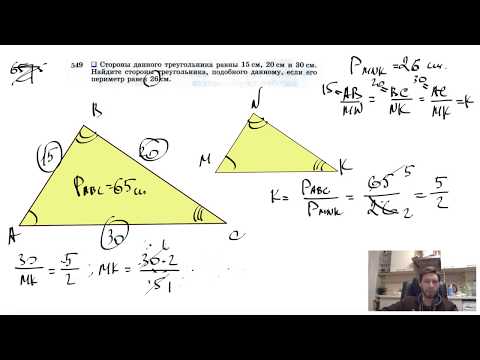
№549. Стороны данного треугольника равны 15 см, 20 см и 30 см. Найдите стороны треугольникаСкачать
Теорема Пифагора для чайников)))Скачать

Формулы равностороннего треугольника #shortsСкачать

Только 1 может решить эту хитрую задачу ★ Найдите углы треугольника ★ Супер ЖЕСТЬСкачать

Как найти сторону треугольника по его периметруСкачать

Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Геометрия 7 класс (Урок№9 - Треугольник.)Скачать

9 класс, 15 урок, Решение треугольниковСкачать

Уравнения стороны треугольника и медианыСкачать




















