Как нарисовать треугольник призма

Главная страница » Основы Академического рисунка » Как построить призму. Правильное изображение фигуры на рисунке

Овладеть базовыми знаниями в области рисунка необходимо каждому начинающему художнику, независимо от выбранного стиля живописи. Обучение рисунку происходит поэтапно, и одной из важнейших тем является построение геометрических фигур. Сначала ученики осваивают плоские объекты, а потом переходят к объемным – в частности, призмам.

В зависимости от фигуры, лежащей в основании, призма бывает треугольной, четырехугольной, пятиугольной и так далее. Рассмотрим процесс рисования на примере четырехгранной и шестигранной призмы.

Видео:УРОК 3.КАК НАРИСОВАТЬ ПРИЗМУ,ПИРАМИДУ.Обучение рисунку.Урок рисования карандашом.построение поэтапноСкачать

Рисуем четырехгранную призму

Четырехгранная призма строится по тому же плану, что и куб, поэтому логично сначала освоить рисование этой фигуры. Обе они – это простые геометрические тела, имеющие прямые грани. Однако если у куба все грани являются квадратами, то у призмы квадраты – это только основания, а боковые грани – прямоугольники.

Объект рисуют в точности так же, как и куб, длина которого затем увеличивается по горизонтали или вертикали (в зависимости от положения предмета).

Как правило, длина увеличивается в полтора раза, однако это зависит от того, во сколько раз высота фигуры превышает ширину основания призмы.

Сначала нужно нанести на лист бумаги общие габариты фигуры при помощи легких линий карандашом.

Видео:Треугольная призма. Ортогональные и изометрическая проекции. Урок 10.(Часть2. ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ)Скачать

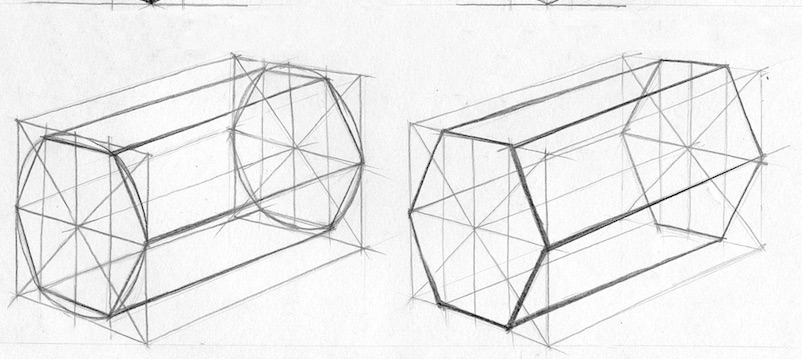
Шестигранная призма

Основой для построения шестигранной призмы является четырехгранная. Передняя поверхность делится пополам по вертикали и горизонтали с учетом перспективы, если тело изображено в ракурсе. Затем вписываем в поверхность эллипс. Горизонтальная ось, пересекающая поверхность, делится еще раз пополам с учетом перспективы. Ставим точки в местах пересечения получившихся вертикалей с окружностью. Соединяем их между собой и с углами.

Точно такой же шестиугольник нужно нарисовать на задней стороне четырехгранной призмы, а затем соединить его с первым нарисованным шестиугольником. Таким образом, у нас получится шестигранная призма, вписанная в четырехгранную.

Чтобы показать объем вашей призмы, нужно обозначить светотени. В первую очередь нужно заштриховать поверхности в тени и те, на которые тень падает. После этого нужно проработать самые освещенные поверхности.

Видео:ТЕМА 5. ПОСТРОЕНИЕ ШЕСТИГРАННОЙ ПРИЗМЫ, КОНУСА И ЧЕТЫРЕХГРАННОЙ ПИРАМИДЫ.Скачать

Зачем уметь строить эту геометрическую фигуру?

Научиться изображать геометрические тела, в том числе и призмы, необходимо всем будущим художникам.

С построения этих объектов начинается учебный процесс во всех заведениях. А уже после этого студенты постепенно переходят к изображению розеток, капителей, портрета и фигуры человека.

Если вы освоите этот объект, то в дальнейшем вам будет проще изображать различные предметы, строящиеся на его основе. В частности, у вас не возникнет трудностей с различными коробками и упаковками, бытовой техникой, зданиями и так далее.

Рисование геометрических тел также входит и в экзаменационную программу для поступления в художественный вуз. Однако с первого раза построить правильную фигуру с соблюдением пропорции и перспективы получается далеко не у каждого. Поэтому будет лучше, если в процессе подготовки к экзаменам вы потратите на изображение призмы достаточно времени, тогда на самом вступительном испытании будете чувствовать себя уверенно. С каждым разом изображение призмы будет даваться все легче.

В школе-студии К.Э. Арутюновой «Мастер рисунка» учат работать с геометрическими телами. К каждому ученику применяется индивидуальный подход с учетом его уровня и времени до сдачи вступительного экзамена. Преподаватель подробно разбирает со студентами все работы, обращает внимание на ошибки и помогает их исправить.

Готовитесь ли вы к поступлению в художественный вуз или просто хотите научиться для себя, без основ вам не обойтись. Независимо от того, в каком стиле вы собираетесь работать позднее, начать изучение все равно необходимо с базовых знаний. Запишитесь на занятия по телефону в Москве или через специальную форму на сайте.

Видео:УРОК 4.Как нарисовать шестигранную ПРИЗМУ.Построение. поэтапно.Обучение рисунку.Рисунок карандашомСкачать

Треугольная призма все формулы и примеры задач

Треугольная призма — это трехмерное тело, образованное соединением прямоугольников и треугольников. В этом уроке вы узнаете, как найти размер внутри (объем) и снаружи (площадь поверхности) треугольной призмы.

Видео:Как сделать объемную ТРЕУГОЛЬНУЮ ПРИЗМУ из бумаги А4? / Объемные геометрические фигуры своими рукамиСкачать

Определение

Треугольная призма — это пятигранник, образованный двумя параллельными плоскостями, в которых расположены два треугольника, образующих две грани призмы, и оставшиеся три грани — параллелограммы, образованные со-сторонами треугольников.

Видео:Как нарисовать пирамиду?Скачать

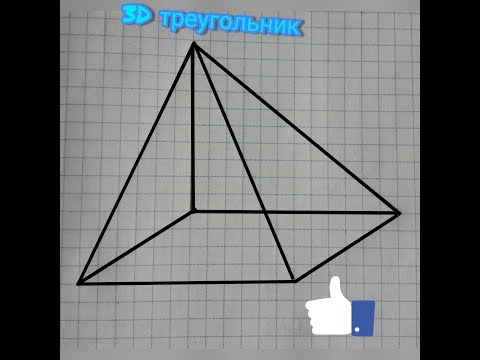
Элементы треугольной призмы

Треугольники ABC и A₁B₁C₁ являются основаниями призмы .

Четырехугольники A₁B₁BA, B₁BCC₁ и A₁C₁CA являются боковыми гранями призмы .

Стороны граней являются ребрами призмы (A₁B₁, A₁C₁, C₁B₁, AA₁, CC₁, BB₁, AB, BC, AC), всего у треугольной призмы 9 граней.

Высотой призмы называется отрезок перпендикуляра, который соединяет две грани призмы (на рисунке это h).

Диагональю призмы называется отрезок, который имеет концы в двух вершинах призмы, не принадлежащих одной грани. У треугольной призмы такой диагонали провести нельзя.

Площадь основания — это площадь треугольной грани призмы.

Площадь боковой поверхности призмы — это сумма площадей четырехугольных граней призмы.

Видео:«КАК РИСОВАТЬ ШЕСТИГРАННУЮ ПИРАМИДУ?» Цикл уроков от Дениса Чернова | Урок №2 | AkademikaСкачать

Виды треугольных призм

Треугольная призма бывает двух видов: прямая и наклонная.

У прямой призмы боковые грани прямоугольники, а у наклонной боковые грани — параллелограммы (см. рис.)

Прямая треугольная призма

Призма, боковые ребра которой перпендикулярны плоскостям оснований, называется прямой.

Наклонная треугольная призма

Призма, боковые ребра которой являются наклонными к плоскостям оснований, называется наклонной.

Видео:Как начертить ПРИЗМУ ТРЕХГРАННУЮСкачать

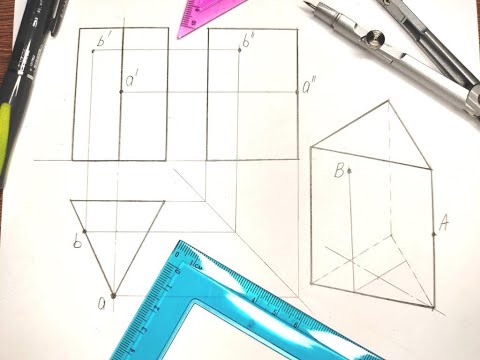
Основные формулы для расчета треугольной призмы

Объем треугольной призмы

Чтобы найти объем треугольной призмы, надо площадь ее основания умножить на высоту призмы.

Объем призмы = площадь основания х высота

Площадь боковой поверхности призмы

Чтобы найти площадь боковой поверхности треугольной призмы, надо периметр ее основания умножить на высоту.

Площадь боковой поверхности треугольной призмы = периметр основания х высота

Площадь полной поверхности призмы

Чтобы найти площадь полной поверхности призмы, надо сложить ее площади оснований и площадь боковой поверхности.

так как S_бок=P_осн . h, то получим:

Правильная призма — прямая призма, основанием которой является правильный многоугольник.

Свойства призмы :

Верхнее и нижнее основания призмы – это равные многоугольники.
Боковые грани призмы имеют вид параллелограмма.
Боковые ребра призмы параллельные и равны.

Совет: при расчете треугольной призмы вы должны обратить внимание на используемые единицы. Например, если площадь основания указана в см 2 , то высота должна быть выражена в сантиметрах, а объем — в см 3 . Если площадь основания в мм 2 , то высота должна быть выражена в мм, а объем в мм 3 и т. д.

Видео:Призма треугольная из картонаСкачать

Пример призмы

В этом примере:
— ABC и DEF составляют треугольные основания призмы
— ABED, BCFE и ACFD являются прямоугольными боковыми гранями
— Боковые края DA, EB и FC соответствуют высоте призмы.
— Точки A, B, C, D, E, F являются вершинами призмы.

Видео:Как сделать объемную ТРЕУГОЛЬНУЮ ПРИЗМУ из бумаги А4? // Геометрические фигуры своими рукамиСкачать

Задачи на расчет треугольной призмы

Задача 1. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, боковое ребро равно 5. Найдите объем призмы.
Решение: Объем прямой призмы равен V = Sh, где S — площадь основания, а h — боковое ребро. Площадь основания в данном случае это площадь прямоугольного треугольника (его площадь равна половине площади прямоугольника со сторонами 6 и 8). Таким образом, объём равен:

V = 1/2 · 6 · 8 · 5 = 120.

Задача 2.

Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Объем отсеченной треугольной призмы равен 5. Найдите объем исходной призмы.

Решение:

Объём призмы равен произведению площади основания на высоту: V = S_осн ·h.

Треугольник, лежащий в основании исходной призмы подобен треугольнику, лежащему в основании отсечённой призмы. Коэффициент подобия равен 2, так как сечение проведено через среднюю линию (линейные размеры большего треугольника в два раза больше линейных размеров меньшего). Известно, что площади подобных фигур соотносятся как квадрат коэффициента подобия, то есть S₂ = S₁k 2 = S₁2 2 = 4S₁.

Площадь основания всей призмы больше площади основания отсечённой призмы в 4 раза. Высоты обеих призм одинаковы, поэтому объем всей призмы в 4 раза больше объема отсечённой призмы.

Таким образом, искомый объём равен 20.

Формулы по математике для ЕГЭ и ОГЭ

Шар и сфера, объем шара, площадь сферы, формулы

Видео:нарисовать 3 треугольника 5 линиями #vshudeyko #newСкачать

Как научиться правильно изображать призму

Старт освоения рисунка и живописи всегда начинается с академического рисунка. Именно это те основы, которые помогают потом создавать картины разной сложности и в разных техниках. Академический рисунок — длительный и постепенный процесс. Начало изучения заключается в рисовании простых геометрических фигур, чаще всего ими выступают гипсовые фигуры. Построение геометрических предметов помогают в дальнейшем реализовывать даже самые сложные задачи. Из простых форм всегда изучают куб, после чего переходят к призмам. Призмы бывают разные, форма зависит от того, как фигура лежит в основании — четырехугольник, пятиугольник и т.д. Сегодня мы расскажем, как правильно изображать призму на разных примерах.

Видео:Треугольная призмаСкачать

Как правильно изобразить четырехгранную призму?

Процесс построения призмы схожий с построением куба, поэтому, если вы справились с данной фигурой, то рисунок четырехгранной призмы будет простым и легким. Схожесть этих фигур — у них обеих прямые грани. У куба все грани квадраты, а у призмы — только основы. Боковые грани — это прямоугольники.

Первым шагом намечаем композицию легкими линиями, затем рисуем основание призмы и уже от произвольной длины основы мы можем измерять высоту призмы. Для того, чтобы понять, какое соотношение сторон, мы можем использовать карандаш на вытянутой руке. Стоит помнить о том, что раскрытие верхнего квадрата будет меньше, нежели раскрытие ниже. Это правило работает, если предмет находится ниже линии горизонта. Нам следует рисовать точные линии, чтобы точки пересечения были четкими. Аккуратность построения будет влиять на то, насколько проработанным будет итоговое изображение.

Видео:Как нарисовать призму / How to draw prismСкачать

Как правильно изобразить шестигранную призму?

Шестигранная призма строится уже значительно сложнее. Можно идти по принципу построения четырехгранной призмы, где сначала обозначается основа, а затем достраиваются боковые грани. Можно строить иначе. Для того, чтобы правильно построить шестигранную призму, мы должны построить четырехгранную.

При этом мы делим переднюю грань пополам, создавая дополнительные грани. Этот способ сложнее, так как ошибка на первом этапе может испортить итоговый результат. Шестигранную призму мы строим с применениями знаний о раскрытии эллипсов, что способствует правильному определению размеров граней. Как и любой предмет, объемность призмы создается с помощью светотени. Начинаем штриховку равномерно, после чего добираем тон в самых темных участках.

Видео:Шестиугольная призма.Ортогональные и изометрическая проекции.Урок 17.(Часть2. ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ)Скачать

Для чего необходимо уметь строить призму?

Призма помогает закрепить знания по рисунку фигур с плоскими формами. При этом закрепляется целый ряд тем и техник. Происходит знакомство с понятием “раскрытие”, оттачивается мастерство аккуратного построения и измерения предметов.

Призма позволяет отработать умения, чтобы научиться изображать реальные предметы, здания, коробки.

🎥 Видео

Треугольник - 3 точки?Скачать

Натюрморт из геометрических предметовСкачать

Построение шестигранной призмыСкачать

Построение призмСкачать

Как нарисовать НЕВОЗМОЖНЫЙ ТРЕУГОЛЬНИК | 3D | Оптическая иллюзияСкачать

3D Пирамида-Треугольник Объемный рисунок по Клеточкам #pixelvideoСкачать