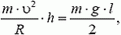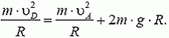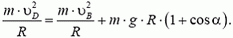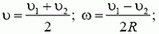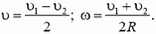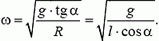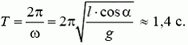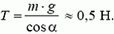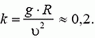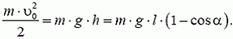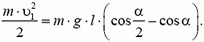Как направлена сила действующая на шарик движущийся по окружности

Физика | 10 — 11 классы

Равнодействующая сила, действующая на шарик, привязанный к нити и движущийся по окружности в горизонтальной плоскости с постоянной по модулю скоростью имеет направление : 1вертикально вниз.

2 горизонтально по касательной к окружности.

3 горизонтально по радиусу к центру окружности.

4равнодействующая равна ноль.

Равнодействующая сила, действующая на шарик, привязанный к нити движущийся с постоянной по модулюскоростью поокружности в горизонтальной скоростью направлена горизонтально по радиусу к центру окружности (mV ^ 2 / R = T + mg — в векторной форме).

Видео:Центростремительное ускорение. 9 класс.Скачать

Если тело движется по окружности с постоянной по модулю скоростью то равнодействующая всех сил действующих на тело 1) равна 0 2)постоянна по модулю и направленна вдоль вектора оси 3) постоянна по моду?

Если тело движется по окружности с постоянной по модулю скоростью то равнодействующая всех сил действующих на тело 1) равна 0 2)постоянна по модулю и направленна вдоль вектора оси 3) постоянна по модулю и направленна по радиусу к центру окружности 4) постоянна по модулю и направлена от центра окружности.

Видео:Физика - движение по окружностиСкачать

, очень надо помогитеШар, подвешенный на нити, равномерно движется по окружности в горизонтальной плоскости?

, очень надо помогите

Шар, подвешенный на нити, равномерно движется по окружности в горизонтальной плоскости.

Какое направление имеет вектор равнодействующей всех сил, приложенных к нему ?

Варианты ответов : 2 Равнодействующая всех сил равна нулю.

Видео:Центробежная силаСкачать

Как направлена равнодействующая сил, приложенных к автомобилю, если он движется горизонтально вправо, равноускоренно прямолинейно с уменьшающейся по модулю скоростью?

Как направлена равнодействующая сил, приложенных к автомобилю, если он движется горизонтально вправо, равноускоренно прямолинейно с уменьшающейся по модулю скоростью?

А. Горизонтально влево

Видео:Урок 90. Движение по окружности (ч.2)Скачать

На тело, находящиееся на горизонтальной плоскости, действуют три горизонтальные силы(см?

На тело, находящиееся на горизонтальной плоскости, действуют три горизонтальные силы(см.

Каков модуль равнодействующей этих сил, если F1 = 1 H.

ОТВЕТ : корень из 10 Н.

Видео:Правило рук 👋 КАК ЛЕГКО определять НАПРАВЛЕНИЕ ЛИНИЙ МАГНИТНОГО ПОЛЯ??Скачать

Шарик массой 200 г, привязанный нитью к подвесу, движется с постоянной скоростью, описывая в горизонтальной плоскости окружность?

Шарик массой 200 г, привязанный нитью к подвесу, движется с постоянной скоростью, описывая в горизонтальной плоскости окружность.

Определите скорость шарика и период его вращения по окружности, если длина нити 1 м, а ее угол с вертикалью составляет 60 градусов.

С подробным решением, пожалуйста.

Видео:Урок 43. Криволинейное движение. Равномерное движение по окружности. Центростремительное ускорениеСкачать

Вагонетка массой 5 т движется с постояннгой по модулю скоростью 5 м / с по горизонтальным рельсам, проложенным по дуге окружности радиусом 100 м?

Вагонетка массой 5 т движется с постояннгой по модулю скоростью 5 м / с по горизонтальным рельсам, проложенным по дуге окружности радиусом 100 м.

Чему равен модуль силы с которой рельсы действуют на вагонетку в направлении на центр окружности?

Видео:Урок 87. Движение по наклонной плоскости (ч.1)Скачать

На движущийся автомобиль в горизонтальном направлении действует сила тяги 1200Н и сила сопротивления движения 1кН?

На движущийся автомобиль в горизонтальном направлении действует сила тяги 1200Н и сила сопротивления движения 1кН.

Чему равна равнодействующая этих сил?

Видео:Урок 89. Движение по окружности (ч.1)Скачать

Самолет летит по окружности в горизонтальной плоскости с постоянной по модулю скоростью?

Самолет летит по окружности в горизонтальной плоскости с постоянной по модулю скоростью.

Как направлен вектор ускорения самолета?

Видео:Правило ПРАВОЙ и ЛЕВОЙ руки. Сила Ампера и Сила Лоренца. ЕГЭ Физика. Николай НьютонСкачать

Самолет летит по окружности в горизонтальной плоскости с постоянной по модулю скоростью?

Самолет летит по окружности в горизонтальной плоскости с постоянной по модулю скоростью.

Как направлен вектор ускорения самолета?

Видео:Отчего он ходит по кругу?Скачать

Шар, подвешенный на нити, движется равномерно по окружности в горизонтальной плоскости?

Шар, подвешенный на нити, движется равномерно по окружности в горизонтальной плоскости.

Какое направление имеет вектор равнодействующей всех приложенных к нему сил.

На этой странице сайта размещен вопрос Равнодействующая сила, действующая на шарик, привязанный к нити и движущийся по окружности в горизонтальной плоскости с постоянной по модулю скоростью имеет направление : 1вертикально вниз? из категории Физика с правильным ответом на него. Уровень сложности вопроса соответствует знаниям учеников 10 — 11 классов. Здесь же находятся ответы по заданному поиску, которые вы найдете с помощью автоматической системы. Одновременно с ответом на ваш вопрос показаны другие, похожие варианты по заданной теме. На этой странице можно обсудить все варианты ответов с другими пользователями сайта и получить от них наиболее полную подсказку.

Видео:Движение тел по окружностиСкачать

Школе NET

Register

Do you already have an account? Login

Login

Don’t you have an account yet? Register

Newsletter

Submit to our newsletter to receive exclusive stories delivered to you inbox!

• Главная 
• Вопросы & Ответы 
• Вопрос 16395497

Энджелл

Видео:ДВИЖЕНИЕ ПО НАКЛОННОЙ ПЛОСКОСТИ | механика 10 классСкачать

1. Заряженный шарик, привязанный к изолирующей нити длины l = 10 см, равномерно движется по окружности, лежащей в горизонтальной плоскости. Масса шарика m = 0,01 г, его заряд q = –9 нКл. Угол отклонения нити от вертикали α = 30°. В точке подвеса нити находится другой шарик с зарядом q0 = 10нКл. Чему равна частота nобращения шарика?

Видео:Сила КориолисаСкачать

Лучший ответ:

Главный Попко

1) во-первых, нужно понимать, какие силы действуют на шарик с зарядом q (пренебрегаем силой натяжения нити).

1. сила тяжести
2. Кулоновская сила, направленная по нити к шарику с зарядом q0 (т.к. заряды на них разноименные)
3. равнодействующая сила, направленная к центру окружности, лежащей в горизонтальной плоскости (шарик движется с центростремительным ускорением)

направляем ось OX в сторону ускорения, получаем (2 закон Ньютона):

следовательно, a = Fsinα / m

при этом Кулоновская сила равна: F = k |q| |q0| / l^2

тогда a = k |q| |q0| sinα / m l^2.

2) так-с, нашли ускорение, теперь нужно связать с ним частоту. проведем следующий мысленный, рандомный вывод формул:

V = l / t = 2πR / T, где V — линейная скорость

заметим, что величина 1/T — это и есть частота обращения v. Тогда:

теперь эту же самую скорость выведем другим способом:

a = V^2 / R => V = sqrt(2aR).

следовательно (приравниваем выражения):

v = sqrt(2aR) / 2πR.

нам неизвестен только радиус. рассмотрим sinα:

sinα = R / l => R = sinα l.

подставляем формулу ускорения и формулу радиуса:

v = sqrt(k |q| |q0| sinα / m l^2) / 2π l sinα,

Видео:Урок 44. Вращение твердого тела. Линейная и угловая скорость. Период и частота вращения.Скачать

Асламазов Л.Г. Движение по окружности // Квант

Асламазов Л.Г. Движение по окружности // Квант. — 1972. — № 9. — С. 51-57.

По специальной договоренности с редколлегией и редакцией журнала «Квант»

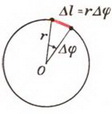
Для описания движения по окружности наряду с линейной скоростью вводят понятие угловой скорости. Если точка при движении по окружности за время Δt описывает дугу, угловая мера которой Δφ, то угловая скорость .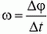

Угловая скорость ω связана с линейной скоростью υ соотношением υ = ω·r, где r — радиус окружности, по которой движется точка (рис. 1). Понятие угловой скорости особенно удобно для описания вращения твердого тела вокруг оси. Хотя линейные скорости у точек, находящихся на разном расстоянии от оси, будут неодинаковыми, их угловые скорости будут равны, и можно говорить об угловой скорости вращения тела в целом.

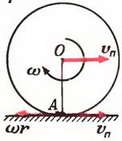
Задача 1. Диск радиуса r катится без проскальзывания по горизонтальной плоскости. Скорость центра диска постоянная и равна υ_п. С какой угловой скоростью при этом вращается диск?

Каждая точка диска участвует в двух движениях — в поступательном движении со скоростью υ_п вместе с центром диска и во вращательном движении вокруг центра с некоторой угловой скоростью ω.

Для нахождения ω воспользуемся отсутствием проскальзывания, то есть тем, что в каждый момент времени скорость точки диска, соприкасающейся с плоскостью, равна нулю. Это означает, что для точки А (рис. 2) скорость поступательного движения υ_п равна по величине и противоположна по направлению линейной скорости вращательного движения υ_вр = ω·r. Отсюда сразу получаем .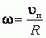

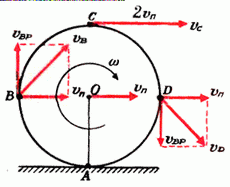
Задача 2. Найти скорости точек В, С и D того же диска (рис. 3).

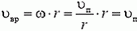
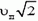
Рассмотрим вначале точку В. Линейная скорость ее вращательного движения направлена вертикально вверх и равна , то есть по величине равна скорости поступательного движения, которая, однако, направлена горизонтально. Складывая векторно эти две скорости, находим, что результирующая скорость υ_B по величине равна и образует угол 45º с горизонтом. У точки С скорости вращательного и поступательного движения направлены в одну сторону. Результирующая скорость υ_C равна 2υ_п и направлена горизонтально. Аналогично находится и скорость точки D (см. рис. 3).

Даже в том случае, когда скорость точки, движущейся по окружности, не меняется по величине, точка имеет некоторое ускорение, так как меняется направление вектора скорости. Это ускорение называется центростремительным. Оно направлено к центру окружности и равно 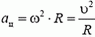(R — радиус окружности, ω и υ — угловая и линейная скорости точки).

Если же скорость точки, движущейся по окружности, меняется не только по направлению, но и по величине, то наряду с центростремительным ускорением существует и так называемое тангенциальное ускорение. Оно направлено по касательной к окружности и равно отношению 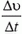(Δυ — изменение величины скорости за время Δt).

Задача 3. Найти ускорения точек А, В, С и D диска радиуса r, катящегося без проскальзывания по горизонтальной плоскости. Скорость центра диска постоянна и равна υ_п (рис. 3).

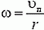
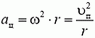
В системе координат, связанной с центром диска, диск вращается с угловой скоростью ω, а плоскость движется поступательно со скоростью υ_п. Проскальзывание между диском и плоскостью отсутствует, следовательно, . Скорость поступательного движения υ_п не меняется, поэтому угловая скорость вращения диска постоянная и точки диска имеют только центростремительное ускорение , направленное к центру диска. Так как система координат движется без ускорения (с постоянной скоростью υ_п), то в неподвижной системе координат ускорения точек диска будут теми же.

Перейдем теперь к задачам на динамику вращательного движения. Вначале рассмотрим простейший случай, когда движение по окружности происходит с постоянной скоростью. Так как ускорение тела при этом направлено к центру, то и векторная сумма всех сил, приложенных к телу, должна быть тоже направлена к центру, и по II закону Ньютона .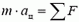

Следует помнить, что в правую часть этого уравнения входят только реальные силы, действующие на данное тело со стороны других тел. Никакой центростремительной силы при движении по окружности не возникает. Этим термином пользуются просто для обозначения равнодействующей сил, приложенных к телу, движущемуся по окружности. Что касается центробежной силы, то она возникает только при описании движения по окружности в неинерциальной (вращающейся) системе координат. Мы пользоваться здесь понятием центростремительной и центробежной силы вообще не будем.

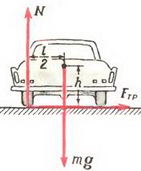
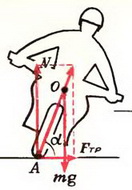
Задача 4. Определить наименьший радиус закругления дороги, которое автомобиль может пройти при скорости υ = 70 км/ч и коэффициенте трения шин о дорогу k =0,3.

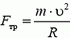
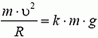
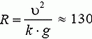
На автомобиль действуют сила тяжести Р = m·g, сила реакции дороги N и сила трения F_тp между шинами автомобиля и дорогой. Силы Р и N направлены вертикально и равны по величине: P = N. Сила трения, препятствующая проскальзыванию («заносу») автомобиля, направлена к центру поворота и сообщает центростремительное ускорение: . Максимальное значение силы трения F_{тр max} = k·N = k·m·g, поэтому минимальное значение радиуса окружности, по которой еще возможно движение со скоростью υ, определяется из уравнения . Отсюда (м).

Сила реакции дороги N при движении автомобиля по окружности не проходит через центр тяжести автомобиля. Это связано с тем, что ее момент относительно центра тяжести должен компенсировать момент силы трения, стремящийся опрокинуть автомобиль. Величина силы трения тем больше, чем больше скорость автомобиля 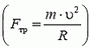. При некотором значении скорости момент силы трения превысит момент силы реакции и автомобиль опрокинется.

Задача 5. При какой скорости автомобиль, движущийся по дуге окружности радиуса R = 130 м, может опрокинуться? Центр тяжести автомобиля находится на высоте h = 1 м над дорогой, ширина следа автомобиля l = 1,5 м (рис. 4).

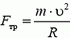
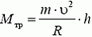
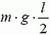
В момент опрокидывания автомобиля как сила реакции дороги N, так и сила трения F_тp приложены к «внешнему» колесу. При движении автомобиля по окружности со скоростью υ на него действует сила трения . Эта сила создает момент относительно центра тяжести автомобиля . Максимальный момент силы реакции дороги N = m·g относительно центра тяжести равен (в момент опрокидывания сила реакции проходит через внешнее колесо). Приравнивая эти моменты, найдем уравнение для максимальной скорости, при которой автомобиль еще не опрокинется:

Откуда 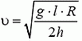≈ 30 м/с ≈ 110 км/ч.

Чтобы автомобиль мог двигаться с такой скоростью, необходим коэффициент трения 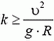(см. предыдущую задачу).

Аналогичная ситуация возникает при повороте мотоцикла или велосипеда. Сила трения, создающая центростремительное ускорение, имеет момент относительно центра тяжести, стремящийся опрокинуть мотоцикл. Поэтому для компенсации этого момента моментом силы реакции дороги мотоциклист наклоняется в сторону поворота (рис. 5).

Задача 6. Мотоциклист едет по горизонтальной дороге со скоростью υ = 70 км/ч, делая поворот радиусом R = 100 м. На какой угол α к горизонту он должен при этом наклониться, чтобы не упасть?

Сила трения между мотоциклом и дорогой 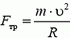, так как она сообщает мотоциклисту центростремительное ускорение. Сила реакции дороги N = m·g. Условие равенства моментов силы трения и силы реакции относительно центра тяжести дает уравнение: F_тp·l·sin α = N·l·cos α, где l — расстояние ОА от центра тяжести до следа мотоцикла (см. рис. 5).

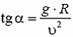
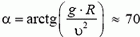
Подставляя сюда значения F_тp и N, находим что или . Отметим, что равнодействующая сил N и F_тp при этом угле наклона мотоцикла проходит через центр тяжести, что и обеспечивает равенство нулю суммарного момента сил N и F_тp.

Для того, чтобы увеличить скорость движения по закруглению дороги, участок дороги на повороте делают наклонным. При этом в создании центростремительного ускорения, кроме силы трения, участвует и сила реакции дороги.

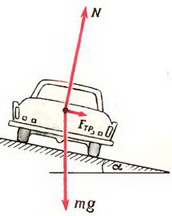
Задача 7. С какой максимальной скоростью υ может двигаться автомобиль по наклонному треку с углом наклона α при радиусе закругления R и коэффициенте трения шин о дорогу k?

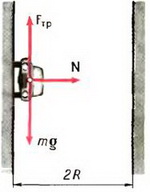
На автомобиль действуют сила тяжести m·g, сила реакции N, направленная перпендикулярно плоскости трека, и сила трения F_тp, направленная вдоль трека (рис. 6).

Так как нас не интересуют в данном случае моменты сил, действующих на автомобиль, мы нарисовали все силы приложенными к центру тяжести автомобиля. Векторная сумма всех сил должна быть направлена к центру окружности, по которой движется автомобиль, и сообщать ему центростремительное ускорение. Поэтому сумма проекций сил на направление к центру (горизонтальное направление) равна 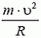, то есть

Сумма проекций всех сил на вертикальное направление равна нулю:

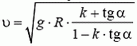
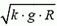
Подставляя в эти уравнения максимальное возможное значение силы трения F_тp = k·N и исключая силу N, находим максимальную скорость , с которой еще возможно движение по такому треку. Это выражение всегда больше значения , соответствующего горизонтальной дороге.

Разобравшись с динамикой поворота, перейдем к задачам на вращательное движение в вертикальной плоскости.

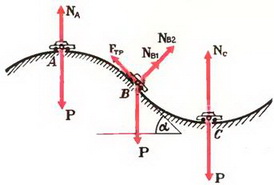
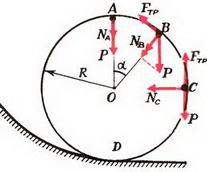
Задача 8. Автомобиль массы m = 1,5 т движется со скоростью υ = 70 км/ч по дороге, показанной на рисунке 7. Участки дороги АВ и ВС можно считать дугами окружностей радиуса R = 200 м, касающимися друг друга в точке В. Определить силу давления автомобиля на дорогу в точках А и С. Как меняется сила давления при прохождении автомобилем точки В?

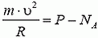
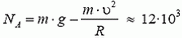
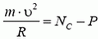
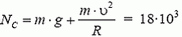
В точке А на автомобиль действуют сила тяжести Р = m·g и сила реакции дороги N_A. Векторная сумма этих сил должна быть направлена к центру окружности, то есть вертикально вниз, и создавать центростремительное ускорение: , откуда (Н). Сила давления автомобиля на дорогу равна по величине и противоположна по направлению силе реакции. В точке С векторная сумма сил направлена вертикально вверх: и (Н). Таким образом, в точке А сила давления меньше силы тяжести, а в точке С — больше.

В точке В автомобиль переходит с выпуклого участка дороги на вогнутый (или наоборот). При движении по выпуклому участку проекция силы тяжести на направление к центру должна превышать силу реакции дороги N_B1, причем 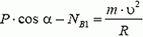. При движении по вогнутому участку дороги, наоборот, сила реакции дороги N_В2 превосходит проекцию силы тяжести: .

Из этих уравнений получаем, что при прохождении точки В сила давления автомобиля на дорогу меняется скачком на величину 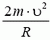≈ 6·10 3 Н. Разумеется, такие ударные нагрузки действуют разрушающе как на автомобиль, так и на дорогу. Поэтому дороги и мосты всегда стараются делать так, чтобы их кривизна менялась плавно.

При движении автомобиля по окружности с постоянной скоростью сумма проекций всех сил на направление, касательное к окружности, должна быть равна нулю. В нашем случае касательная составляющая силы тяжести уравновешивается силой трения между колесами автомобиля и дорогой.

Величина силы трения регулируется вращательным моментом, прикладываемым к колесам со стороны мотора. Этот момент стремится вызвать проскальзывание колес относительно дороги. Поэтому возникает сила трения, препятствующая проскальзыванию и пропорциональная приложенному моменту. Максимальное значение силы трения равно k·N, где k — коэффициент трения между шинами автомобиля и дорогой, N — сила давления на дорогу. При движении автомобиля вниз сила трения играет роль тормозящей силы, а при движении вверх, наоборот, роль силы тяги.

Задача 9. Автомобиль массой m = 0,5 т, движущийся со скоростью υ = 200 км/ч, совершает «мертвую петлю» радиуса R = 100 м (рис. 8). Определить силу давления автомобиля на дорогу в верхней точке петли А; в точке В, радиус-вектор которой составляет угол α = 30º с вертикалью; в точке С, в которой скорость автомобиля направлена вертикально. Возможно ли движение автомобиля по петле с такой постоянной скоростью при коэффициенте трения шин о дорогу k = 0,5?

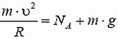
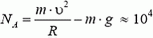
В верхней точке петли сила тяжести и сила реакции дороги N_A направлены вертикально вниз. Сумма этих сил создает центростремительное ускорение: . Поэтому Н.

Сила давления автомобиля на дорогу равна по величине и противоположна по направлению силе N_А.

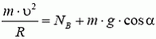
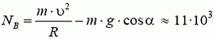
В точке В центростремительное ускорение создается суммой силы реакции и проекции силы тяжести на направление к центру: . Отсюда Н.

Легко видеть, что N_B > N_A; с увеличением угла α сила реакции дороги увеличивается.

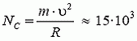
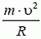
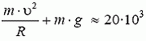
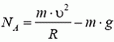
В точке С сила реакции Н; центростремительное ускорение в этой точке создается только силой реакции, а сила тяжести направлена по касательной. При движении по нижней части петли сила реакции будет превышать и максимальное значение Н сила реакции имеет в точке D. Значение , таким образом, является минимальным значением силы реакции.

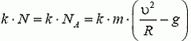
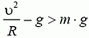
Скорость автомобиля будет постоянной, если касательная составляющая силы тяжести не превышает максимальной силы трения k·N во всех точках петли. Это условие заведомо выполняется, если минимальное значение превосходит максимальное значение касательной составляющей силы веса. В нашем случае это максимальное значение равно m·g (оно достигается в точке С), и условие выполняется при k = 0,5, υ = 200 км/ч, R = 100 м.

Таким образом, в нашем случае движение автомобиля по «мертвой петле» с постоянной скоростью возможно.

Рассмотрим теперь движение автомобиля по «мертвой петле» с выключенным мотором. Как уже отмечалось, обычно момент силы трения противодействует моменту, приложенному к колесам со стороны мотора. При движении автомобиля с выключенным мотором этого момента нет, и силой трения между колесами автомобиля и дорогой можно пренебречь.

Скорость автомобиля уже не будет постоянной — касательная составляющая силы тяжести замедляет или ускоряет движение автомобиля по «мертвой петле». Центростремительное ускорение тоже будет меняться. Создается оно, как обычно, равнодействующей силы реакции дороги и проекции силы тяжести на направление к центру петли.

Задача 10. Какую наименьшую скорость должен иметь автомобиль в нижней точке петли D (см. рис. 8) для того, чтобы совершить ее с выключенным мотором? Чему будет равна при этом сила давления автомобиля на дорогу в точке В? Радиус петли R = 100 м, масса автомобиля m = 0,5 т.

Посмотрим, какую минимальную скорость может иметь автомобиль в верхней точке петли А, чтобы продолжать двигаться по окружности?

Центростремительное ускорение в этой точке дороги создается суммой силы тяжести и силы реакции дороги . Чем меньшую скорость имеет автомобиль, тем меньшая возникает сила реакции N_A. При значении эта сила обращается в нуль. При меньшей скорости сила тяжести превысит значение, необходимое для создания центростремительного ускорения, и автомобиль оторвется от дороги. При скорости сила реакции дороги обращается в нуль только в верхней точке петли. В самом деле, скорость автомобиля на других участках петли будет большей, и как легко видеть из решения предыдущей задачи, сила реакции дороги 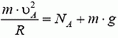тоже будет большей, чем в точке А. Поэтому, если автомобиль в верхней точке петли имеет скорость , то он нигде не оторвется от петли.

Теперь определим, какую скорость должен иметь автомобиль в нижней точке петли D, чтобы в верхней точке петли А его скорость . Для нахождения скорости υ_D можно воспользоваться законом сохранения энергии, как если бы автомобиль двигался только под действием силы тяжести. Дело в том, что сила реакции дороги в каждый момент направлена перпендикулярно перемещению автомобиля, а, следовательно, ее работа равна нулю (напомним, что работа ΔA = F·Δs·cos α, где α — угол между силой F и направлением перемещения Δs). Силой трения между колесами автомобиля и дорогой при движении с выключенным мотором можно пренебречь. Поэтому сумма потенциальной и кинетической энергии автомобиля при движении с выключенным мотором не меняется.

Приравняем значения энергии автомобиля в точках А и D. При этом будем отсчитывать высоту от уровня точки D, то есть потенциальную энергию автомобиля в этой точке будем считать равной нулю. Тогда получаем

Подставляя сюда значение для искомой скорости υ_D, находим: ≈ 70 м/с ≈ 260 км/ч.

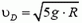
Если автомобиль въедет в петлю с такой скоростью, то он сможет совершить ее с выключенным мотором.

Определим теперь, с какой силой при этом автомобиль будет давить на дорогу в точке В. Скорость автомобиля в точке В опять легко находится из закона сохранения энергии:

Подставляя сюда значение 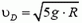, находим, что скорость .

Воспользовавшись решением предыдущей задачи, по заданной скорости находим силу давления в точке B:

Н.

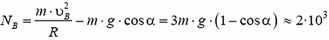
Аналогично можно найти силу давления в любой другой точке «мертвой петли».

1. Найти угловую скорость искусственного спутника Земли, вращающегося по круговой орбите с периодом обращения Т = 88 мин. Найти линейную скорость движения этого спутника, если известно, что его орбита расположена на расстоянии R = 200 км от поверхности Земли.

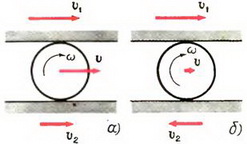
2. Диск радиуса R помещен между двумя параллельными рейками. Рейки движутся со скоростями υ₁ и υ₂. Определить угловую скорость вращения диска и скорость его центра. Проскальзывание отсутствует.

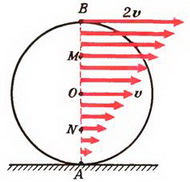
3. Диск катится по горизонтальной поверхности без проскальзывания. Показать, что концы векторов скоростей точек вертикального диаметра находятся на одной прямой.

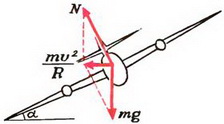
4. Самолет движется по окружности с постоянной горизонтальной скоростью υ = 700 км/час. Определить радиус R этой окружности, если корпус самолета наклонен на угол α = 5°.

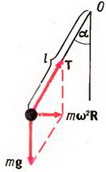
5. Груз массы m = 100 г, подвешенный на нити длины l = 1 м, равномерно вращается по кругу в горизонтальной плоскости. Найти период обращения груза, если при его вращении нить отклонена по вертикали на угол α = 30°. Определить также натяжение нити.

6. Автомобиль движется со скоростью υ = 80 км/ч по внутренней поверхности вертикального цилиндра радиуса R = 10 м по горизонтальному кругу. При каком минимальном коэффициенте трения между шинами автомобиля и поверхностью цилиндра это возможно?

7. Груз массой m подвешен на нерастяжимой нити, максимально возможное натяжение которой равно 1,5m·g. На какой максимальный угол α можно отклонить нить от вертикали, чтобы при дальнейшем движении груза нить не оборвалась? Чему будет равно при этом натяжение нити в тот момент, когда нить составит угол α/2 с вертикалью?

I. Угловая скорость искусственного спутника Земли 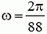≈ 0,071 рад/с. Линейная скорость спутника υ = ω·R. где R — радиус орбиты. Подставляя сюда R = R₃ + h, где R₃ ≈ 6400 км, находим υ ≈ 467 км/с.

2. Здесь возможны два случая (рис. 1). Если угловая скорость диска ω, а скорость его центра υ, то скорости точек, соприкасающихся с рейками, будут соответственно равны

(Мы приняли для определенности, что υ₁ > υ₂). Решая эти системы, находим:

а)

б)

3. Скорость любой точки М, лежащей на отрезке ОВ (см. рис. 2), находится по формуле υ_M = υ + ω·r_M, где r_M — расстояние от точки М до центра диска О. Для любой точки N, принадлежащей отрезку ОА, имеем: υ_N = υ – ω·r_N, где r_N — расстояние от точки N до центра. Обозначим через ρ расстояние от любой точки диаметра ВА до точки А соприкосновения диска с плоскостью. Тогда очевидно, что r_M = ρ – R и r_N = R – ρ = –(ρ – R). где R — радиус диска. Поэтому скорость любой точки на диаметре ВА находится по формуле: υ_ρ = υ + ω·(ρ – R). Так как диск катится без проскальзывания, то 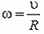и для скорости υ_ρ получаем υ_ρ = ω·ρ. Отсюда следует, что концы векторов скоростей находятся на прямой, выходящей из точки А и наклоненной к диаметру ВА под углом, пропорциональным угловой скорости вращения диска ω.

Доказанное утверждение позволяет нам сделать вывод, что сложное движение точек, находящихся на диаметре ВА, можно в каждый данный момент рассматривать как простое вращение вокруг неподвижной точки А с угловой скоростью ω, равной угловой скорости вращения вокруг центра диска. В самом деле, в каждый момент скорости этих точек направлены перпендикулярно диаметру ВА, а по величине равны произведению ω на расстояние до точки А.

Оказывается, что это утверждение справедливо для любой точки диска. Более того, оно является общим правилом. При любом движении твердого тела в каждый момент существует ось, вокруг которой тело просто вращается — мгновенная ось вращения.

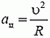
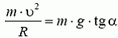
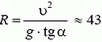
4. На самолет действуют (см. рис. 3) сила тяжести Р = m·g и подъемная сила N, направленная перпендикулярно плоскости крыльев (так как самолет движется с постоянной скоростью, то сила тяги и сила лобового сопротивления воздуха уравновешивают друг друга). Равнодействующая сил Р и N должна быть направлена к центру окружности, по которой движется самолет, и создавать центростремительное ускорение . Из рисунка находим:

или км.

5. Равнодействующая силы тяжести Р = m·g и силы натяжения нити Т должна создавать центростремительное ускорение а_ц = ω 2 ·R, где R = l·sin α — радиус круга, по которому вращается груз. Из рисунка 4 получаем:

m·ω 2 ·R = m·g·tg α, откуда

Период обращения груза

Натяжение нити

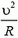
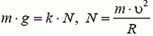
6. На автомобиль действуют (рис. 5) сила тяжести Р = m·g, сила реакции со стороны цилиндра N и сила трения F_тp. Так как автомобиль движется по горизонтальному кругу, то силы Р и F_тp уравновешивают друг друга, а сила N создает центростремительное ускорение . Максимальное значение силы трения связано с силой реакции N соотношением: F_тp = k·N. В результате получаем систему уравнений: , из которой находится минимальное значение коэффициента трения

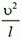
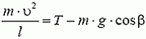
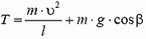
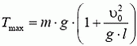
7. Груз будет двигаться по окружности радиуса l (рис. 6). Центростремительное ускорение груза (υ — скорость груза) создается разностью величин силы натяжения нити Т и проекции силы тяжести m·g направление нити: . Поэтому , где β — угол, образуемый нитью с вертикалью. По мере того, как груз будет опускаться, его скорость будет расти, а угол β будет уменьшаться. Натяжение нити станет максимальным при угле β = 0 (в тот момент, когда нить будет вертикальной): . Максимальная скорость груза υ₀ находится по углу α, на который отклоняют нить, из закона сохранения энергии:

Используя это соотношение, для максимального значения натяжения нити получаем формулу: T_max = m·g·(3 – 2 cos α). По условию задачи T_mах = 2m·g. Приравнивая эти выражения, находим cos α = 0,5 и, следовательно, α = 60°.

Определим теперь натяжение нити при 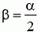. Скорость груза в этот момент также находится из закона сохранения энергии:

Подставляя значение υ₁ в формулу для силы натяжения, находим:

📸 Видео

Шар на движущейся доскеСкачать

ДВИЖЕНИЕ ПО ОКРУЖНОСТИ 9 класс физика ПерышкинСкачать

Формулы механики 2, движение по окружности, центростремительное ускорениеСкачать

Урок 101. Скатывание тела с наклонной плоскостиСкачать

Урок 63. Перегрузка. Вес тела на полюсе и на экватореСкачать

Урок 93. Основное уравнение динамики вращательного движенияСкачать