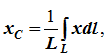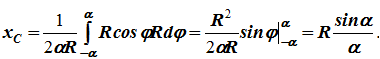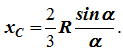Как находить центр тяжести окружности (5 видео)

iSopromat.ru

Формулы для расчета координат положения центра тяжести треугольника, дуги окружности и кругового сегмента.

Содержание

Центр тяжести треугольника
Центр тяжести дуги окружности
Центр тяжести кругового сектора
Тема 1.5. Центр тяжести тела
Вычисление элементов плоских фигур. Площадь. Центр тяжести. Ключевые размеры.Квадрат. Прямоугольник. Параллелограмм. Треугольник. Трапеция. Правильный шестиугольник. Правильный многоугольник. Круг. Полукруг. Сектор. Сегмент. Кольцо. Кольц.сектор. Эллипс
🎬 Видео

Видео:Определение центра тяжести сложной фигуры. СопроматСкачать

Центр тяжести треугольника

Центр тяжести площади треугольника совпадает с точкой пересечения его медиан (рисунок 1.10, а).

Видео:Видеоурок 3. Определение центра тяжести.Скачать

Центр тяжести дуги окружности

Дуга имеет ось симметрии (рисунок 1.10, б). Центр тяжести лежит на этой оси, т.е. y_C = 0.

dl – элемент дуги, dl = Rdφ, R – радиус окружности, x = Rcosφ, L = 2αR,

Видео:Найти центр кругаСкачать

Центр тяжести кругового сектора

Сектор радиуса R с центральным углом 2α имеет ось симметрии Ox, на которой находится центр тяжести (рисунок 1.10, в).

Разбиваем сектор на элементарные секторы, которые можно считать треугольниками. Центры тяжести элементарных секторов располагаются на дуге окружности радиуса (2/3)R.

Центр тяжести сектора совпадает с центром тяжести дуги AB:

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Видео:Обязательно запомни эту хитрость! Как можно легко и точно найти центр круглой заготовки? #shortsСкачать

Тема 1.5. Центр тяжести тела

§1. Центр тяжести однородного тела.

Рассмотрим твердое тело весом P и объемом V в системе координат Oxyz , где оси x и y связаны с поверхностью земли, а ось z направлена в зенит.

Если разбить тело на элементарные части объемом ∆V_i , то на каждую его часть будет действовать сила притяжения ∆P_i, направленная к центру Земли. Предположим, что размеры тела значительно меньше размеров Земли, тогда систему сил, приложенных к элементарным частям тела можно считать не сходящейся, а параллельной (рис.1), и к ней применимы все выводы предыдущей главы.

Рис.1. Параллельная система сил

Центром тяжести твердого тела называется центр параллельных сил тяжести элементарных частей этого тела.

При определении центра тяжести полезны несколько теорем.

1) Если однородное тело имеет плоскость симметрии, то центр тяжести его находится в этой

2) Если однородное тело имеет ось симметрии, то центр тяжести тела находится на этой оси.

3) Если однородное тело имеет центр симметрии, то центр тяжести тела находится в этой точке.

§2. Способы определения координат центра тяжести.

1. Симметрия. Если однородное тело имеет плоскость, ось или центр симметрии (рис.2), то его центр тяжести лежит соответственно в плоскости симметрии, оси симметрии или в центре симметрии.

Рис.2. Центр тяжести тел, имеющих ось симметрии

2. Разбиение. Тело разбивается на конечное число частей (рис.3), для каждой из которых положение центра тяжести и площадь известны.

Рис.3. Центр тяжести сплошной

сложной геометрической фигуры

— центр тяжести и площадь первой фигуры;

— центр тяжести и площадь второй фигуры;

— координата центра тяжести сплошной сложной геометрической фигуры по оси x;

— координата центра тяжести сплошной сложной геометрической фигуры по оси y;

3. Метод отрицательных площадей. Частный случай способа разбиения (рис.4). Он применяется к телам, имеющим вырезы, если центры тяжести тела без выреза и вырезанной части известны. Тело в виде пластинки с вырезом представляют комбинацией сплошной пластинки (без выреза) с площадью S₁ и площади вырезанной части S₂ .

Рис.4. Центр тяжести сложной геометрической фигуры,

— центр тяжести и площадь первой фигуры;

— центр тяжести и площадь второй фигуры;

— координата центра тяжести сложной геометрической фигуры по оси x;

— координата центра тяжести сложной геометрической фигуры по оси y;

§3. Координаты центра тяжести некоторых простых фигур.

1. Центр тяжести треугольника. Центр тяжести треугольника лежит в точке пересечения его медиан (рис.5). Координаты центра тяжести треугольника представляют собой среднее арифметическое из координат его вершин: x_c =1/3(x₁+x₂+x₃) ; y_c =1/3(y₁+y₂+y₃).

Рис.5. Центр тяжести треугольника

2. Центр тяжести прямоугольника. Центр тяжести прямоугольника лежит в точке пересечения его диагоналей (рис.6). Координаты центра тяжести прямоугольника рассчитываются по формулам: x_c =b/2 ; y_c =h/2.

Рис. 6. Центр тяжести треугольника

3. Центр тяжести полукруга. Центр тяжести полукруга лежит на оси симметрии (рис.7). Координаты центра тяжести полукруга рассчитываются по формулам: x_c =D/2 ; y_c =4R/3π.

Рис. 7. Центр тяжести полукруга

4. Центр тяжести круга. Центр тяжести круга лежит в центре (рис.8). Координаты центра тяжести круга рассчитываются по формулам: x_c =R ; y_c =R.

Рис. 8. Центр тяжести круга

Вопросы для самопроверки:

— Что называется центром параллельных сил?

— Что называется центром тяжести тела?

— Почему силы притяжения Земле, действующие на точку тела, можно принять за систему параллельных сил?

— Запишите формулу для определения положения центра тяжести неоднородных и однородных тел, формулу для определения положения центра тяжести плоских сечений?

— Запишите формулу для определения положения центра тяжести простых геометрических фигур: прямоугольника, квадрата, трапеции и половины круга?

— Как используются свойства симметрии при определении центров тяжести тел?

— В чем состоит сущность способа отрицательных площадей?

— Каким графическим построением можно найти центр тяжести треугольника?

— Запишите формулу, определяющую центр тяжести треугольника.

Видео:Как найти центр тяжести любой фигуры?Скачать

Вычисление элементов плоских фигур. Площадь. Центр тяжести. Ключевые размеры.Квадрат. Прямоугольник. Параллелограмм. Треугольник. Трапеция. Правильный шестиугольник. Правильный многоугольник. Круг. Полукруг. Сектор. Сегмент. Кольцо. Кольц.сектор. Эллипс

Вычисление элементов плоских фигур. Площадь. Центр тяжести. Ключевые размеры.Квадрат. Прямоугольник. Параллелограмм. Треугольник. Трапеция. Правильный шестиугольник. Правильный многоугольник. Круг. Полукруг. Сектор. Сегмент. Кольцо. Кольцевой сектор. Эллипс.