Как начертить треугольник в окружности

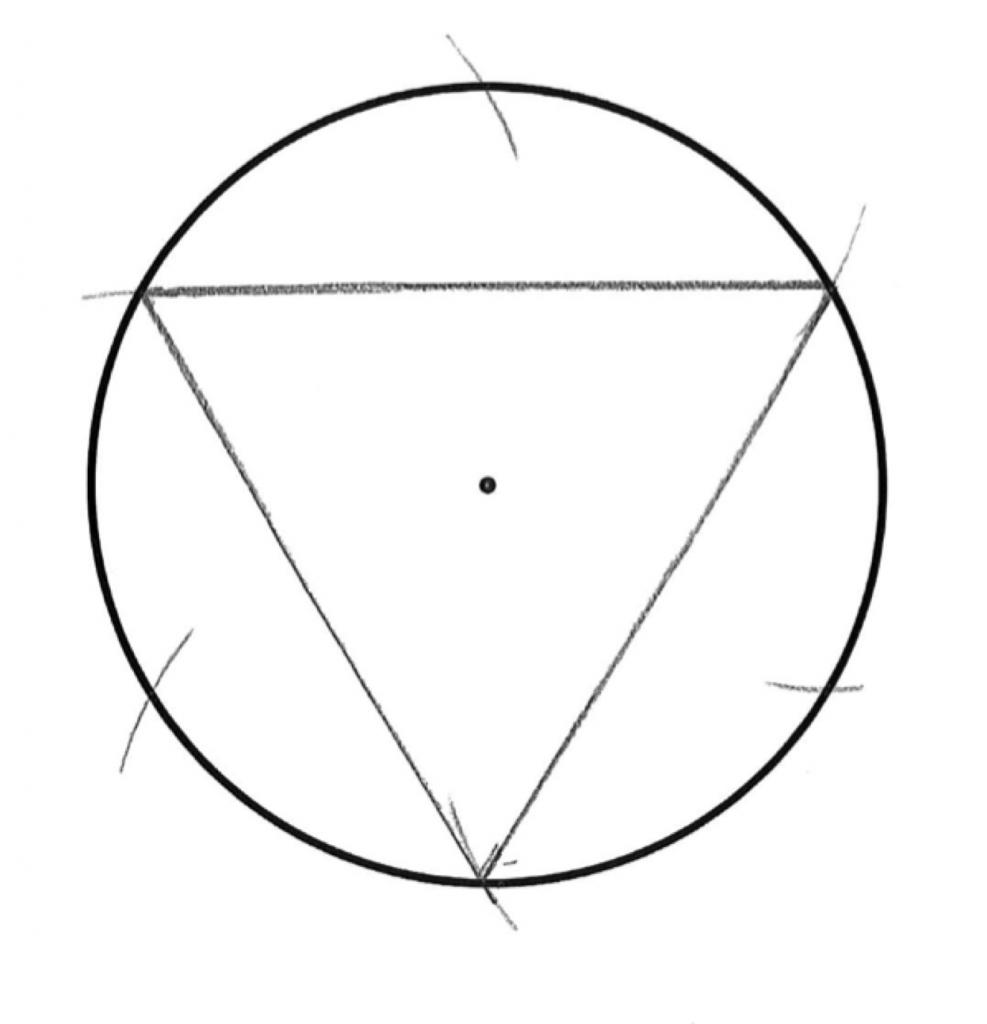
Из этого материала вы узнаете, как с помощью циркуля построить правильный треугольник. Напомним, что треугольник является правильным, если длина всех его сторон одинакова, а каждый из углов составляет 60°.

На листе бумаги отметьте произвольную точку. Установите в эту точку иглу циркуля и нарисуйте окружность.

Установите иглу циркуля в любую произвольную точку, лежащую на окружности, и нарисуйте вторую окружность с центром в этой точке.

При этом не меняйте раствор циркуля, то есть радиус первой окружности должен быть равен радиусу второй окружности.

Отметьте точки пересечения окружностей.

Соедините полученные точки линией. Полученный отрезок будет первой стороной треугольника.

Далее, через центры обеих окружностей нужно провести прямую линию.

Таким образом, у вас получилось три точки, которые будут тремя вершинами треугольника.

Соедините все три точки между собой.

Полученный треугольник имеет одинаковую длину сторон, а величина каждого его угла составляет 60°, а значит он правильный.

Видео:Как поделить окружность на 3 равные части. Очень просто. Уроки черчения.Скачать

Как нарисовать правильный треугольник вписанный в окружность

Popular

Основы черчения

Строительное

Машиностроительное

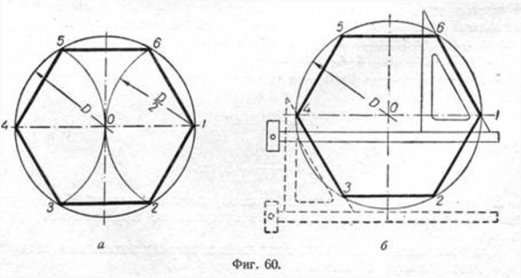
Построение вписанного в окружность правильного шестиуголь­ника. Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения доста­точно разделить окружность на шесть равных частей и соединить най­денные точки между собой (фиг. 60, а).

Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг. 60, б), строим стороны 1 —6, 4—3, 4—5 и 7—2, после чего прово­дим стороны 5—6 и 3—2.

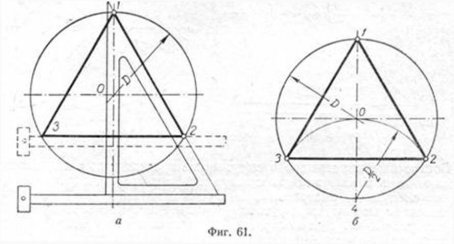
Построение вписанного в окружность равностороннего треуголь­ника. Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного цир­куля.

Рассмотрим два способа построения вписанного в окружность рав­ностороннего треугольника.

Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, прове­дённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0—1—2 равен 30°, то для нахождения стороны

1—2 достаточно построить по точке 1 и стороне 0—1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1—2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2—3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 прово­дим прямую, которая определит третью вершину треугольника.

Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вер­шины через одну, то получится равносторонний треугольник.

Для построения треугольника (фиг. 61, б) намечаем на диаметре вершину—точку 1 и проводим диаметральную линию 1—4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окруж­ностью в точках 3 и 2. Полученные точки будут двумя другими вер­шинами искомого треугольника.

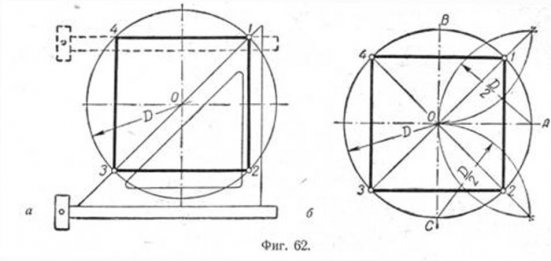
Построение квадрата, вписанного в окружность. Это построение можно выполнить при помощи угольника и циркуля.

Первый способ основан на том, что диагонали квадрата пере­секаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные сто­роны квадрата 4—1 и 3—2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1—2 и 4—3.

Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра (фиг. 62, б). Намечаем на концах двух взаимно перпендикулярных диа­метров точки А, В и С и из них радиусом у описываем дуги до вза­имного их пересечения.

Далее через точки пересечения дуг проводим вспомогательные пря­мые, отмеченные на фигуре сплошными линиями. Точки их пересече­ния с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.

Построение вписанного в окружность правильного пятиугольника.

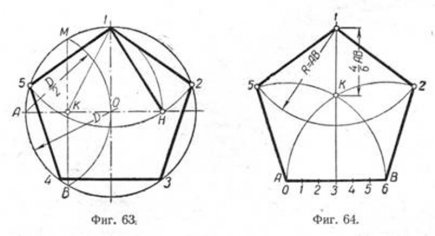
Чтобы вписать в окружность правильный пятиугольник (фиг. 63), про­изводим следующие построения.

Намечаем на окружности точку 1 и принимаем её за одну из вер­шин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точ­ках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вер­шины 3 и 4. Найденные точки последовательно соединяем между собой.

Построение правильного пятиугольника по данной его стороне.

Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую.

Далее от точки К на этой прямой откладываем отрезок, равный 4/6 AB.

Получим точку 1—вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведён­ными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.

Построение вписанного в окружность правильного семиугольника.

Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг. 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиу­сом, равным диаметру окружности D, описываем дугу до пересечения с про­должением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, прово­дим из полюса F через чётные деления вертикального диаметра лучи, пересече­ние которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем после­довательно между собой. Семиугольник может быть построен путём проведе­ния лучей из полюса F и через нечётные деления вертикального диаметра.

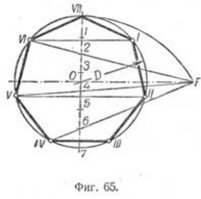
Приведённый способ годен для построения правильных многоуголь­ников с любым числом сторон.

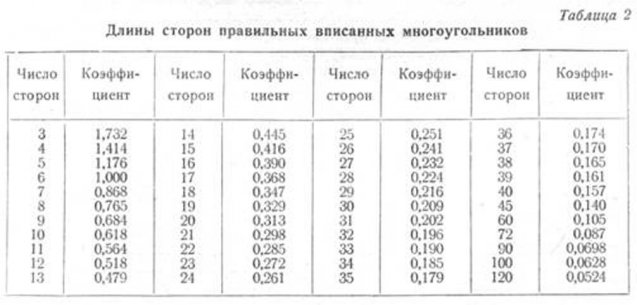
Деление окружности на любое число равных частей можно произ­водить также, пользуясь данными табл. 2, в которой приведены коэф­фициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.

В первой колонке этой таблицы указаны числа сторон правильного вписанного многоугольника, а во второй—коэффициенты.

Длина стороны заданного многоугольника получится от умножения радиуса данной окружности на коэффициент, соответствующий числу сторон этого многоугольника.

Деление окружности на равные части и по­строение правильных вписанных многоуголь­ников можно выполнить как циркулем, так и с помощью угольников и рейсшины.

Деление окружности на четыре равные части и построение пра­вильного вписанного четырех­угольника. Две взаимно перпендикулярные центровые линии делят окружность на четыре равные части (рис. 115, а). Соединив точки пе­ресечения этих линий с окружностью прямы­ми, получают правильный вписанный четырех­угольник.

Деление окружности на восемь равных частей и построение пра­вильного вписанного восьмиуголь­ника. Две взаимно перпендикулярные линии, проведенные под углом 45° к центровым ли­ниям с помощью угольника с углами 45, 45 и 90° и рейсшины (рис. 115, б), вместе с центро­выми линиями разделят окружность на восемь равных частей.

Деление окружности на восемь равных час­тей можно выполнить циркулем. Для этого из точек 1 и 3 (точки пересечения центровых линий с окружностью) произвольным радиусом делаются засечки до взаимного пересечения, тем же радиусом делают две засечки из точек 3 и 5 (рис. 115, в). Через точки пересечения засечек и центр окружности проводят прямые линии до пересечения с окружностью в точках 2, 4, 6, 8.

Если полученные восемь точек соединить последовательно прямыми линиями, то полу­чится правильный вписанный восьмиугольник (рис. 115, в).

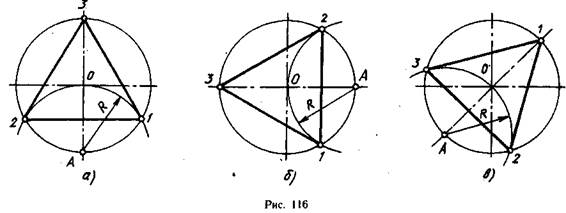
Деление окружности на три рав­ные части и построение правиль­ного вписанного треугольника вы­полняют с помощью циркуля или угольника с углами 30, 60 и 90° и рейсшины.

При делении окружности циркулем на три равные части из любой точки окружности, на­пример из точки Л пересечения центровых ли­ний с окружностью (рис. 116, а и б), проводят дугу радиусом R, равным радиусу данной ок­ружности, получают точки 1 и 2. Третья точка деления (точка 3) будет находиться на про­тивоположном конце диаметра, проходящего через точку Л. Последовательно соединив точ­ки 1, 2 и 3, получают правильный вписанный треугольник. При построении правильного впи­санного треугольника, если задана одна из его вершин, например точка 1, находят точку А. Для этого через заданную точку 1 проводят диаметр (рис. 116, в). Точка А будет находить­ся на противоположном конце этого диаметра. Затем проводят дугу радиусом R равным ра­диусу данной окружности, получают точки 2 и 3.

При делении окружности на три равные час­ти с помощью угольника и рейсшины через точку 1 под углом 60° проводят две прямые линии до пересечения с окружностью в точках 2 и 3 (рис. 117, а, б), точки 2 и 3 соединяют и получают правильный вписанный треугольник (рис. 117, в).

Деление окружности на шесть равных частей и построение пра­вильного вписанного шестиуголь­ника выполняют с помощью угольника с уг­лами 30, 60 и 90° и рейсшины или циркуля. При делении окружности на шесть равных частей циркулем из двух концов одного диа­метра радиусом, равным радиусу данной окруж­ности, проводят дуги до пересечения с окруж­ностью в точках 2, 6 и 3, 5 (рис. 118). Последовательно соединив полученные точки, полу­чают правильный вписанный шестиугольник. Деление окружности на шесть равных час-1ен и построение правильного вписанного шестиугольника с помощью угольника и рейс­шины показано на рис. 119 и 120. Деление окружности на двенад­цать равных частей и построение правильного вписанного двенад­цатиугольника выполняют с помощью угольника с углами 30, 60 и 90° и рейсшины или циркуля.

При делении окружности циркулем из четы­рех концов двух взаимно перпендикулярных диаметров окружности проводят радиусом, рав­ным радиусу данной окружности, дуги до пере­сечения с окружностью (рис. 121). Соединив по­лученные точки, получают двенадцатиугольник.

При построении двенадцатиугольника с по­мощью угольника и рейсшины точки деления строят, как показано на рис. 119 и 120.

Деление окружности на пять и десять равных частей и построе­ние правильного вписанного пяти­угольника и десятиугольника пока­зано на рис. 122.

Половину любого диаметра (радиус) делят пополам (рис. 122, а), получают точку А. Из точки А, как из центра, проводят дугу радиу­сом, равным расстоянию от точки А до точки 1, до пересечения со второй половиной этого диаметра, в точке В (рис. 122, б). Отрезок 1В равен хорде, стягивающей дугу, длина которой равна 1 /₅ длины окружности. Делая засечки на окружности (рис. 122, в) радиусом R, равным отрезку 1В, делят окруж­ность на пять равных частей. Начальную точку 1 выбирают в зависимости от расположения пятиугольника. Из точки / строят точки 2 и 5 (рис. 122, в), затем из точки 2 строят точку 3, а из точки 5 строят точку 4. Расстояние от точки 3 до точки 4 проверяют циркулем; если расстояние между точками 3 и 4 равно отрезку 1В, то построения были выполнены точно. Нельзя выполнять засечки последовательно, в одну сторону, так как происходит набегание ошибок и последняя сторона пятиугольника получается перекошенной. Последовательно соединив найденные точки, получают пяти­угольник (рис. 122, г).

Деление окружности на десять равных час­тей выполняют аналогично делению окруж­ности на пять равных частей (рис. 122), но сначала делят окружность на пять частей, на­чиная построение из точки /, а затем из точ­ки 6, находящейся на противоположном конце диаметра (рис. 123, а). Соединив последова­тельно все точки, получают правильный впи­санный десятиугольник (рис. 123, б).

Деление окружности на семь и четырнадцать равных частей и по­строение правильного вписанного семиугольника и четырнадцатиугольника показано на рис. 124 и 125.

Из любой точки окружности, например точ­ки Л, радиусом заданной окружности проводят дугу (рис. 124, а) до пересечения с окруж­ностью в точках В и D. Соединим точки В и D прямой. Половина полученного отрезка (в данном случае отрезок ВС) будет равна хорде, которая стягивает дугу, составляющую 1 /₇ дли­ны окружности. Радиусом, равным отрезку ВС, делают засечки на окружности в последова­тельности, показанной на рис. 124, б. Соединив последовательно все точки, получают правиль­ный вписанный семиугольник (рис. 124, в).

Деление окружности на четырнадцать рав­ных частей выполняется делением окружности на семь равных частей два раза от двух точек (рис. 125, а).

Сначала окружность делится на семь рав­ных частей от точки /, затем то же построение выполняется от точки 8. Построенные точки соединяют последовательно прямыми линиями и получают правильный вписанный четырна-дцатиугольник (рис. 125, б).

СОПРЯЖЕНИЯ

Рассматривая детали, видим, что в их конст­рукции часто одна поверхность переходит в другую. Обычно эти переходы делают плав­ными, что повышает прочность деталей и де­лает их более удобными в работе. На чертеже поверхности изображаются линиями, которые также плавно переходят одна в другую.

На рис. 126, а изображена деталь, в которой плавные переходы одних плоскостей в другие представляют собой цилиндрические поверхнос­ти. На чертеже (рис. 126, б) эти плоскости изо­бражены прямыми линиями, а цилиндрические поверхности — дугами окружностей. Плавные переходы от одной прямой к другой в этих случаях выполняются дугой заданного радиуса.

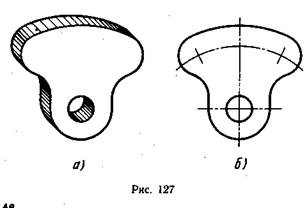
Плавный переход одной цилиндрической поверхности в другую может являться цилинд­рической поверхностью (рис. 127, а). На черте­же эти цилиндрические поверхности изобра­жены дугами окружностей, (рис. 127, б). В этом случае плавный переход одной дуги окруж­ности в другую осуществляется дугой окруж­ности заданного радиуса.

На рис. 126, а и 127, а рассмотрены простей­шие примеры плавных переходов поверхностей. В чертежах более сложных деталей плавные переходы между поверхностями изображают­ся различными сочетаниями прямых, окруж­ностей и их дуг. Вариантов таких сочетаний может быть много, но их объединяет од­но — плавность перехода. Такой плавный пе­реход одной линии (поверхности) в другую ли­нию (поверхность) называют сопряжени­ем. При построении сопряжения необходимо определить границу, где кончается одна линия и начинается другая, т. е. найти на чертеже точку перехода, которая называется точкой сопряжения или точкой касания.

Задачи на сопряжения условно можно раз­делить на три группы.

Первая группа задачвключает в себя зада­чи на построение сопряжений, где участвуют прямые линии. Это может быть непосредствен­ное касание прямой и окружности, сопряжение двух прямых дугой заданного радиуса, а также проведение касательной прямой к двум окружностям.

Построение окружности, каса­тельной к прямой, связано с нахождени­ем точки касания и центра окружности.

Задана горизонтальная прямая АВ, требует­ся построить окружность радиусом R, касательную к данной прямой (рис. 128). Точка касания выбирается произвольно. Так как точка касания не задана, то окружность ра­диуса R может коснуться данной прямой в любой точке. Таких окружностей можно про­вести множество. Центры этих окружностей (O₁, О₂ и т. д.) будут находиться на одина­ковом расстоянии от заданной прямой, т. е. на линии, расположенной параллельно заданной прямой АВ на расстоянии, равном радиусу заданной окружности (рис. 128). Назовем эту линию линией центров. Проведем линию центров параллельно прямой АВ на расстоя­нии R. Так как центр касательной окруж­ности не задан, возьмем любую точку на линии центров, например точку О. Прежде чем про­водить касательную окружность, следует опре­делить точку касания. Точка касания будет лежать на перпендикуляре, опущенном из точ­ки О на прямую АВ. В пересечении перпендику­ляра с прямой АВ получим точку К, которая будет точкой касания. Из центра О радиусом R от точки К проведем окружность. Задача решена.

В детали, которая изображена на рис. 129, а, пластина плавно переходит в цилиндр. При выполнении чертежа этой детали необходимо построить плавный переход прямой в окруж­ность.

Задача аналогична предыдущей, но до­полнена условием, что точка касания задана, так как задан размер А (рис. 129, б), который определяет величину прямолинейного участка.

Отложив размер Л, находят точку касания (точку /С), затем из точки К восставляют пер­пендикуляр, на котором откладывают радиус R заданной окружности, и находят центр ок­ружности (точку О). При обводке сначала от точки касания проводится дуга заданного ра­диуса, а потом — прямая.

Из сказанного следует:

1) центр окружности, касательной к прямой, лежит на прямой (линия центров), проведенной параллельно заданной прямой, на расстоянии, равном радиусу данной окружности;

Не нашли то, что искали? Воспользуйтесь поиском:

Как нарисовать треугольник? Этому учат в процессе изучения геометрии в школе. Чтобы задание было выполнено правильно, важно точно знать, какой треугольник необходимо изобразить: равносторонний, равнобедренный или же вписанный. Правилам начертания этих фигур будет посвящена данная статья.

Видео:Как разделить окружность на 3 равные части или как вписать равнобедренный треугольник в окружностьСкачать

Как рисовать треугольник с равными сторонами?

Как нарисовать треугольник, стороны у которого равны? Для этого можно воспользоваться одним из трех методов.

Такая фигура имеет три одинаковые по длине стороны, связанные тремя углами равной ширины. Это может быть сложным для рисования треугольника вручную. Поэтому можно использовать круглый объект для выделения углов.

Видео:Построение равностронего треугольника.Скачать

Варианты создания фигуры

Обязательно используйте линейку и один из представленных ниже способов:

1. Применение циркуля: надо начертить ровную линию. Проведите карандаш вдоль прямого края бумаги. Этот сегмент линии образует одну из сторон. А это означает, что нужно будет чертить вторую и третью линии одинаковой длины, каждая из которых достигает точки под углом 60° от первой линии. Удостоверьтесь, что достаточно места для рисования всех трех сторон!
2. Разделите сегмент циркулем. Вставьте карандаш и убедитесь, что он острый! Поместите точку циркуля на один конец сегмента и установите карандаш на другую. Опишите дугу. Не изменяйте установленную «ширину» инструмента от точки циркуля до точки карандаша. Нарисуйте вторую дугу, чтобы она пересекала первую дугу, которую уже нарисовали. Отметьте точку, в которой пересекаются две дуги. Это вершина (верхняя точка) треугольника. Он должен лежать в точном центре сегмента линии, который нарисовали. Теперь можете сделать две прямые линии, ведущие к этой точке: по одному от каждого конца «нижнего» сегмента линии. Закончите треугольник. Далее с помощью линейки надо нарисовать еще два сегмента прямой линии – это стороны в треугольнике. Подключите каждый конец исходного сегмента линии к точке, в которой пересекаются дуги. Чтобы закончить работу, сотрите дуги, которые нарисовали, так, чтобы остался только треугольник.
3. Использование объекта с круглой базой: этот совет подойдет для построения дуги. Предложенный метод по сути такой же, как с использованием циркуля.

Указанные советы помогут выяснить, как нарисовать равносторонний треугольник.

Видео:Деление окружности на 3; 6; 12 равных частейСкачать

Рекомендации по построению равнобедренного треугольника

Равнобедренный треугольник представляет собой фигуру с двумя равными сторонами и двумя равными углами. Если знаете длину, основание и высоту стороны, это можно сделать только с линейкой и циркулем (или просто циркулем, если заданы размеры).

Как нарисовать равнобедренный треугольник:

1. Учитывая все боковые длины. Чтобы использовать этот метод, важно знать длину основания треугольника и длину двух равных сторон.
2. Учитывая две равные стороны и угол между ними. Чтобы использовать этот метод, нужно знать длину двух равных сторон и измерение угла между этими двумя сторонами.
3. Учитывая базовые и смежные углы – необходимо знать длину базы, градусы двух углов, смежных с основанием. Помните, что два угла, смежные с основанием равнобедренного треугольника, будут равны.
4. Основа и высота. Нужно знать длину основания треугольника, а также высоту этой геометрической фигуры.

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Вписанный треугольник

Как нарисовать вписанный треугольник? Выберите круглый объект. Используйте предмет с круглым основанием. Выбор компакт-диска станет хорошим вариантом. Но можно взять и другой объект нужного размера. Для этого метода свойственно, что длина каждой стороны равносторонней геометрической фигуры с тремя углами будет равна размерам радиуса (половине диаметра) круга.

Как нарисовать треугольник, если используете компакт-диск? Представьте себе равносторонний треугольник, который вписывается в верхнюю правую часть компакт-диска. Надо начертить первую из сторон. Радиус круглого объекта – расстояние на полпути до получения желаемого результата. Удостоверьтесь, что линии нарисованы ровно.

С помощью линейки просто выполните измерения диаметра объекта и нарисуйте линию на половину длины. Если ее нет, поместите круглый объект на бумагу, затем тщательно проведите по окружности карандашом. Удалите объект – должен быть идеальный круг. Используйте прямой край, чтобы нарисовать линию через точный центр круга: точку, которая полностью равноудалена от любой точки по окружности круга.

Используйте круглый объект для создания дуги. Поместите объект по отрезку линии, с краем круга, расположенным на одном конце линии. Для обеспечения точности убедитесь, что линия проходит четко через центр круга. Используйте карандаш, чтобы начертить дугу – это четверть пути по окружности.

Начертите еще одну дугу. Теперь сдвиньте круглый объект так, чтобы край касался другого конца сегмента линии.

Видео:Деление окружности на равные части. Урок 6. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Подведем итоги

В статье были предоставлены рекомендации, как нарисовать треугольник равносторонний, равнобедренный и вписанный в окружность.

Видео:Геометрия - Построение правильного треугольникаСкачать

Треугольник вписанный в окружность

Видео:Построить описанную окружность (Задача 1)Скачать

Определение

Треугольник, вписанный в окружность — это треугольник, который
находится внутри окружности и соприкасается с ней всеми тремя вершинами.

На рисунке 1 изображена окружность, описанная около
треугольника и окружность, вписанная в треугольник.

ВD = FC = AE — диаметры описанной около треугольника окружности.

O — центр вписанной в треугольник окружности.

Видео:Как построить правильный равнобедренный треугольник с помощью окружности, чертежи, черчениеСкачать

Формулы

Радиус вписанной окружности в треугольник

r — радиус вписанной окружности.

1. Радиус вписанной окружности в треугольник,
   если известна площадь и все стороны:

Радиус вписанной окружности в треугольник,
если известны площадь и периметр:

Радиус вписанной окружности в треугольник,
если известны полупериметр и все стороны:

Радиус описанной окружности около треугольника

R — радиус описанной окружности.

1. Радиус описанной окружности около треугольника,
   если известна одна из сторон и синус противолежащего стороне угла:

Радиус описанной окружности около треугольника,
если известны все стороны и площадь:

Радиус описанной окружности около треугольника,
если известны все стороны и полупериметр:

Площадь треугольника

S — площадь треугольника.

1. Площадь треугольника вписанного в окружность,
   если известен полупериметр и радиус вписанной окружности:

Площадь треугольника вписанного в окружность,
если известен полупериметр:

Площадь треугольника вписанного в окружность,
если известен высота и основание:

Площадь треугольника вписанного в окружность,
если известна сторона и два прилежащих к ней угла:

Площадь треугольника вписанного в окружность,
если известны две стороны и синус угла между ними:

[ S = fracab cdot sin angle C ]

Периметр треугольника

P — периметр треугольника.

1. Периметр треугольника вписанного в окружность,
   если известны все стороны:
   

Периметр треугольника вписанного в окружность,
если известна площадь и радиус вписанной окружности:

Периметр треугольника вписанного в окружность,
если известны две стороны и угол между ними:

Сторона треугольника

a — сторона треугольника.

1. Сторона треугольника вписанного в окружность,
   если известны две стороны и косинус угла между ними:

Сторона треугольника вписанного в
окружность, если известна сторона и два угла:

Средняя линия треугольника

l — средняя линия треугольника.

1. Средняя линия треугольника вписанного
   в окружность, если известно основание:
   

Средняя линия треугольника вписанного в окружность,
если известныдве стороны, ни одна из них не является
основанием, и косинус угламежду ними:

Высота треугольника

h — высота треугольника.

1. Высота треугольника вписанного в окружность,
   если известна площадь и основание:

Высота треугольника вписанного в окружность,
если известен сторона и синус угла прилежащего
к этой стороне, и находящегося напротив высоты:

[ h = b cdot sin alpha ]

Высота треугольника вписанного в окружность,
если известен радиус описанной окружности и
две стороны, ни одна из которых не является основанием:

Видео:Деление окружности на 3, 4, 5, 6 и 7 равных частейСкачать

Свойства

• Центр вписанной в треугольник окружности
  находится на пересечении биссектрис.
• В треугольник, вписанный в окружность,
  можно вписать окружность, причем только одну.
• Для треугольника, вписанного в окружность,
  справедлива Теорема Синусов, Теорема Косинусов
  и Теорема Пифагора.
• Центр описанной около треугольника окружности
  находится на пересечении серединных перпендикуляров.
• Все вершины треугольника, вписанного
  в окружность, лежат на окружности.
• Сумма всех углов треугольника — 180 градусов.
• Площадь треугольника вокруг которого описана окружность, и
  треугольника, в который вписана окружность, можно найти по
  формуле Герона.

Видео:Вписанная и описанная около равнобедренного треугольника, окружностьСкачать

Доказательство

Около любого треугольника, можно
описать окружность притом только одну.

окружность и треугольник,
которые изображены на рисунке 2.

окружность описана
около треугольника.

1. Проведем серединные
   перпендикуляры — HO, FO, EO.
2. O — точка пересечения серединных
   перпендикуляров равноудалена от
   всех вершин треугольника.
3. Центр окружности — точка пересечения
   серединных перпендикуляров — около
   треугольника описана окружность — O,
   от центра окружности к вершинам можно
   провести равные отрезки — радиусы — OB, OA, OC.

окружность описана около треугольника,
что и требовалось доказать.

Подводя итог, можно сказать, что треугольник,
вписанный в окружность — это треугольник,
в котором все серединные перпендикуляры
пересекаются в одной точке, и эта точка
равноудалена от всех вершин треугольника.

💥 Видео

№711. Начертите три треугольника: тупоугольный, прямоугольный и равносторонний. ДляСкачать

Строим вписанную в данный треугольник окружность (Задача 2).Скачать

Равносторонний треугольник в окружностиСкачать

Построение высоты в тупоугольном и прямоугольном треугольниках. 7 класс.Скачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

Построение высоты в треугольникеСкачать

Как построить правильный шестиугольник.Скачать

Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Построение медианы в треугольникеСкачать