Как начертить остроугольный треугольник и вписать в него окружность

Видео:№711. Начертите три треугольника: тупоугольный, прямоугольный и равносторонний. ДляСкачать

Треугольник вписанный в окружность

Видео:Построить описанную окружность (Задача 1)Скачать

Определение

Треугольник, вписанный в окружность — это треугольник, который
находится внутри окружности и соприкасается с ней всеми тремя вершинами.

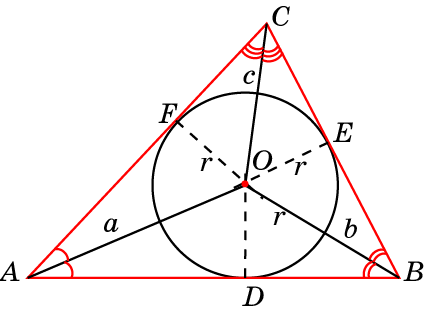
На рисунке 1 изображена окружность, описанная около
треугольника и окружность, вписанная в треугольник.

ВD = FC = AE — диаметры описанной около треугольника окружности.

O — центр вписанной в треугольник окружности.

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Формулы

Радиус вписанной окружности в треугольник

r — радиус вписанной окружности.

1. Радиус вписанной окружности в треугольник,
   если известна площадь и все стороны:

Радиус вписанной окружности в треугольник,
если известны площадь и периметр:

Радиус вписанной окружности в треугольник,
если известны полупериметр и все стороны:

Радиус описанной окружности около треугольника

R — радиус описанной окружности.

1. Радиус описанной окружности около треугольника,
   если известна одна из сторон и синус противолежащего стороне угла:

Радиус описанной окружности около треугольника,
если известны все стороны и площадь:

Радиус описанной окружности около треугольника,
если известны все стороны и полупериметр:

Площадь треугольника

S — площадь треугольника.

1. Площадь треугольника вписанного в окружность,
   если известен полупериметр и радиус вписанной окружности:

Площадь треугольника вписанного в окружность,
если известен полупериметр:

Площадь треугольника вписанного в окружность,
если известен высота и основание:

Площадь треугольника вписанного в окружность,
если известна сторона и два прилежащих к ней угла:

Площадь треугольника вписанного в окружность,
если известны две стороны и синус угла между ними:

[ S = frac ab cdot sin angle C ]

Периметр треугольника

P — периметр треугольника.

1. Периметр треугольника вписанного в окружность,
   если известны все стороны:
   

Периметр треугольника вписанного в окружность,
если известна площадь и радиус вписанной окружности:

Периметр треугольника вписанного в окружность,
если известны две стороны и угол между ними:

Сторона треугольника

a — сторона треугольника.

1. Сторона треугольника вписанного в окружность,
   если известны две стороны и косинус угла между ними:

Сторона треугольника вписанного в
окружность, если известна сторона и два угла:

Средняя линия треугольника

l — средняя линия треугольника.

1. Средняя линия треугольника вписанного
   в окружность, если известно основание:
   

Средняя линия треугольника вписанного в окружность,
если известныдве стороны, ни одна из них не является
основанием, и косинус угламежду ними:

Высота треугольника

h — высота треугольника.

1. Высота треугольника вписанного в окружность,
   если известна площадь и основание:

Высота треугольника вписанного в окружность,
если известен сторона и синус угла прилежащего
к этой стороне, и находящегося напротив высоты:

[ h = b cdot sin alpha ]

Высота треугольника вписанного в окружность,
если известен радиус описанной окружности и
две стороны, ни одна из которых не является основанием:

Видео:Построение равностронего треугольника.Скачать

Свойства

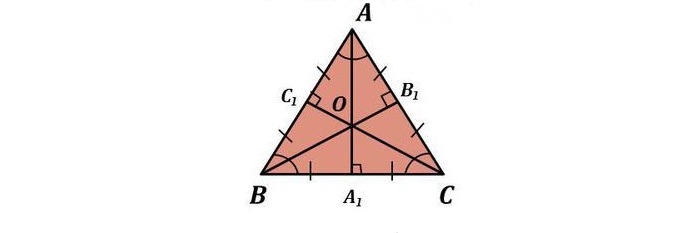
• Центр вписанной в треугольник окружности
  находится на пересечении биссектрис.
• В треугольник, вписанный в окружность,
  можно вписать окружность, причем только одну.
• Для треугольника, вписанного в окружность,
  справедлива Теорема Синусов, Теорема Косинусов
  и Теорема Пифагора.
• Центр описанной около треугольника окружности
  находится на пересечении серединных перпендикуляров.
• Все вершины треугольника, вписанного
  в окружность, лежат на окружности.
• Сумма всех углов треугольника — 180 градусов.
• Площадь треугольника вокруг которого описана окружность, и
  треугольника, в который вписана окружность, можно найти по
  формуле Герона.

Видео:Как разделить окружность на 3 равные части или как вписать равнобедренный треугольник в окружностьСкачать

Доказательство

Около любого треугольника, можно
описать окружность притом только одну.

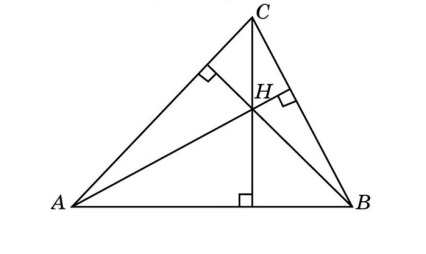
окружность и треугольник,
которые изображены на рисунке 2.

окружность описана
около треугольника.

1. Проведем серединные
   перпендикуляры — HO, FO, EO.
2. O — точка пересечения серединных
   перпендикуляров равноудалена от
   всех вершин треугольника.
3. Центр окружности — точка пересечения
   серединных перпендикуляров — около
   треугольника описана окружность — O,
   от центра окружности к вершинам можно
   провести равные отрезки — радиусы — OB, OA, OC.

окружность описана около треугольника,
что и требовалось доказать.

Подводя итог, можно сказать, что треугольник,
вписанный в окружность — это треугольник,
в котором все серединные перпендикуляры
пересекаются в одной точке, и эта точка
равноудалена от всех вершин треугольника.

Видео:Строим вписанную в данный треугольник окружность (Задача 2).Скачать

Окружность, вписанная в треугольник

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Видео:№701. Начертите три треугольника: остроугольный, прямоугольный и тупоугольный. В каждыйСкачать

«Снятие эмоционального напряжения
у детей и подростков с помощью арт-практик
и психологических упражнений»

Сертификат и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Окружность, вписанная в треугольник

Окружность называется вписанной в треугольник, если все стороны треугольника касаются окружности. A B C O

A B C D F E M N O K r r r Как вписать в окружность треугольник В треугольник можно вписать окружность, и притом только одну. Её центр – точка пересечения биссектрис треугольника. Проведём биссектрисы треугольника: АK, ВM, СN. Построим перпендикуляры ОD, OE, OF, которые равны между собой, т.к. равны соответствующие треугольники. Получаем ОD= OE= OF=r.

Алгоритм построения вписанной окружности в треугольник 1.Строим две биссектрисы треугольника. Точка пересечения — центр вписанной окружности. 2. Строим перпендикуляр на основание из точки пересечения. 3. Этот перпендикуляр является радиусом вписанной окружности. 4. Строим вписанную окружность.

Задача №1 Построить вписанную окружность в: 1. остроугольный треугольник; 2. тупоугольный треугольник; 3. прямоугольный треугольник. Самостоятельная работа Построить вписанную окружность в: 1. остроугольный равнобедренный треугольник; 2. тупоугольный равнобедренный треугольник; 3. прямоугольный равнобедренный треугольник.

Положение центра вписанной окружности

Краткое описание документа:

Презентация по геометрии для урока в 8 классе создана для наглядного изучения вопроса о том, как вписать окружность в треугольник. В ней просто и доходчиво доказывается, что центром окружности, вписанной в треугольник, является точка пересечения биссектрис треугольника. Важная часть презентации — это то, что в ней показан алгоритм построения окружности, вписанной в треугольник. В презентации есть три задачи для закрепления нового материала. Также даны задачи для самостоятельной работы, решение которых поможет ребятам ещё лучше разобраться в новой теме. Последний слайд обращает внимание ребят на положение центра окружности, вписанной в треугольник.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 942 человека из 79 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 316 человек из 68 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 691 человек из 75 регионов

Ищем педагогов в команду «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 489 444 материала в базе

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Дистанционные курсы для педагогов

Другие материалы

• 13.05.2015
• 3537

• 13.05.2015
• 764

• 13.05.2015
• 601

• 13.05.2015
• 3372

• 13.05.2015
• 1210

• 13.05.2015
• 621

• 13.05.2015
• 701

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 13.05.2015 6265 —> —> —> —>
• PPTX 227.7 кбайт —> —>
• Рейтинг: 5 из 5
• Оцените материал:

Настоящий материал опубликован пользователем Сазонова Татьяна Фёдоровна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 7 лет
• Подписчики: 0
• Всего просмотров: 30224
• Всего материалов: 17

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Как поделить окружность на 3 равные части. Очень просто. Уроки черчения.Скачать

Дистанционные курсы
для педагогов

548 курсов от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Петербурге дали рекомендации по переводу школьников на дистант

Время чтения: 3 минуты

В России утвердили новые правила аккредитации образовательных учреждений

Время чтения: 1 минута

В Роспотребнадзоре заявили о широком распространении COVID-19 среди детей

Время чтения: 1 минута

В России могут создать комиссию по поддержке одаренных детей

Время чтения: 1 минута

Пандемия позволила детям получить больше внимания со стороны родителей

Время чтения: 1 минута

Свободное движение повышает креативность

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:Геометрия - Построение правильного треугольникаСкачать

Начертите окружность радиуса 3 см и впишите в неё 1) остроугольный треугольник 2) тупоугольный треугольник.

Видео:Построить окружность, вписанную в треугольникСкачать

Ваш ответ

Видео:Вписанная и описанная окружность - от bezbotvyСкачать

решение вопроса

Видео:Построение высоты в тупоугольном и прямоугольном треугольниках. 7 класс.Скачать

Похожие вопросы

• Все категории
• экономические 43,277
• гуманитарные 33,618
• юридические 17,900
• школьный раздел 606,929
• разное 16,829

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:Окружность и треугольникСкачать

Остроугольный треугольник — виды, свойства и признаки

Одна из центральных тем на уроках геометрии – остроугольный треугольник, составная часть своих более сложных аналогов и иных тригонометрических форм.

Азы изучения точной науки начинаются с рассмотрения уникальной комбинации из трех сторон и острых углов.

Видео:Как построить шестиугольник вписанный в окружностьСкачать

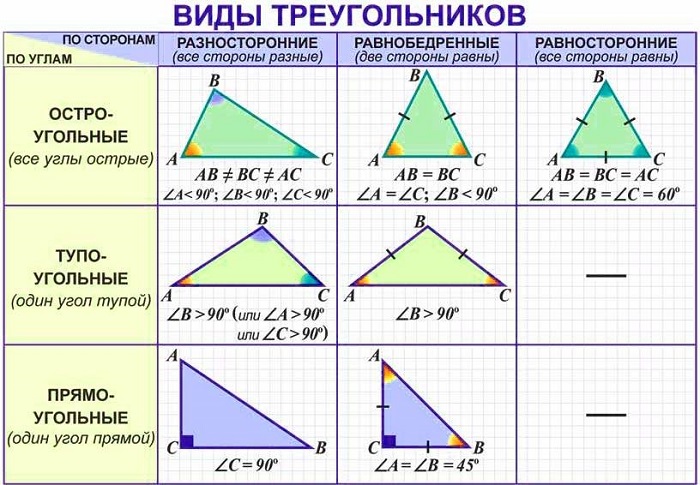
Виды, признаки и свойства остроугольных треугольников

Трехсторонние фигуры разделяются на множество подвидов и категорий.

Общая классификация по наибольшему углу делит их на 3 группы:

Они располагают как общими для формы с тремя сторонами характеристиками, так и специфическими признаками.

3 угла, сумма которых равна 180°, (величина каждого меньше 90°) и 3 стороны;

сумма длин любых двух сторон больше оставшейся третьей.

Свойства остроугольной фигуры определяются вспомогательными геометрическими линиями, всегда находящимися внутри него:

1. Биссектрисы, делящие углы пополам, являются центром, вокруг которого можно нарисовать вписанную окружность.

2. Высоты пересекаются в одной точке, образуя ортоцентр.

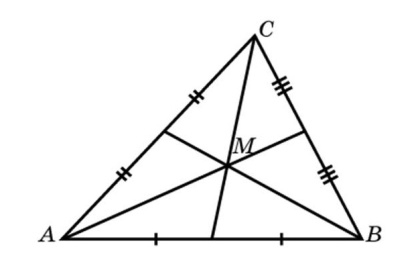
3. Медианы в точке пересечения пролегают в пропорции 2:1 (2 трети до центра и 1 треть после).

Уникальные особенности зависят от разновидностей фигуры.

Видео:Виды треугольников: остроугольный, прямоугольный ,тупоугольный. Как начертить треугольникСкачать

Равносторонний треугольник

«Идеальный» правильный треугольник, облегчающий решение задач. Определение, форма и свойства данной геометрической формы исходят из названия — все углы равны 60°, а стороны равны друг другу.

Полное равенство придает и другую особенность: медианы, биссектрисы и высоты полностью совпадают.

Видео:Как построить окружность, описанную около треугольника, в программе ГЕОГЕБРАСкачать

Разносторонний треугольник

Наиболее часто встречаемый на чертежах в геометрии вариант, один из самых трудноразрешимых видов. Разносторонними бывают и прямоугольные, и тупоугольные фигуры.

Уникальных отличий не имеет, только общие:

все параметры имеют разные значения;

совпадений между вспомогательными линиями нет.

Видео:Вписанный в окружность прямоугольный треугольник.Скачать

Равнобедренный остроугольный треугольник

Здесь при основании (стороне, не равной остальным) находятся равные друг другу 2 стороны и 2 угла. Выглядит как вытянутый в одну сторону равносторонний треугольник.

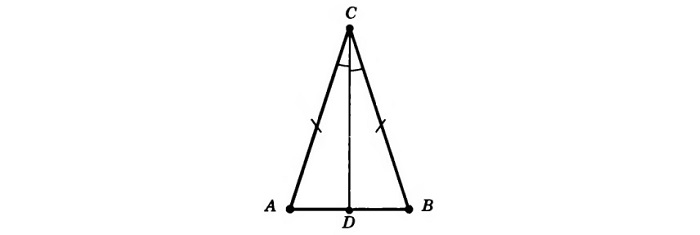
проведенная к основанию линия – и биссектриса, и высота, и медиана;

вспомогательные линии из крайних точек при основании совпадают.

Видео:Вписанная и описанная около равнобедренного треугольника, окружностьСкачать

Равнобедренный тупоугольный треугольник

Пусть он и называется равнобедренным, но из-за наличия угла более 90° не является остроугольным и является представителем другой группы.

Начертить его сложнее (рисунок следует начинать с основания и 2 острых углов и уже после создавать тупой), но процесс решения и изучения прост.

Отличие у него одно – точка пересечения двух высот, проведенных от углов при основании, выходит за периметр треугольника. Чтобы ее обозначить, необходимо нарисовать «продолжения» равнобедренных линий. Все остальные свойства совпадают.

В ключевых и фундаментальных разделах математики именно треугольник является основой для доказательства многих теорем и помощью в решении множества задач. Твердое знание его свойств откроет путь к успехам в расчетах, вычислениях, оформлении чертежей и фото в проектных работах.

Видео:Высоты треугольника.Скачать

Вписанные и описанные треугольники. Еще две формулы площади треугольника. Теорема синусов

Вписанный треугольник — треугольник, все вершины которого лежат на окружности. Тогда окружность называется описанной вокруг треугольника.

Очевидно, расстояние от центра описанной окружности до каждой из вершин треугольника одинаково и равно радиусу этой окружности.

Вокруг любого треугольника можно описать окружность, причем только одну.

Окружность вписана в треугольник, если она касается всех его сторон. Тогда сам треугольник будет описанным вокруг окружности. Расстояние от центра вписанной окружности до каждой из сторон треугольника равно радиусу этой окружности.

В любой треугольник можно вписать окружность, причем только одну.

Попробуйте сами описать окружность вокруг треугольника и вписать окружность в треугольник.

Как вы думаете, почему центр вписанной окружности — это точка пересечения биссектрис треугольника, а центр описанной окружности — точка пересечения серединных перпендикуляров к его сторонам?

В задачах ЕГЭ чаще всего встречаются вписанные и описанные правильные треугольники.

Есть и другие задачи. Для их решения вам понадобятся еще две формулы площади треугольника, а также теорема синусов.

Вот еще две формулы для площади.
Площадь треугольника равна половине произведения его периметра на радиус вписанной окружности.

— радиус окружности, вписанной в треугольник.

Есть и еще одна формула, применяемая в основном в задачах части :

где — стороны треугольника, — радиус описанной окружности.

Для любого треугольника верна теорема синусов:

Ты нашел то, что искал? Поделись с друзьями!

. Радиус окружности, вписанной в равнобедренный прямоугольный треугольник, равен . Найдите гипотенузу c этого треугольника. В ответе укажите .

Треугольник прямоугольный и равнобедренный. Значит, его катеты одинаковы. Пусть каждый катет равен . Тогда гипотенуза равна .

Запишем площадь треугольника АВС двумя способами:

Приравняв эти выражения, получим, что . Поскольку , получаем, что . Тогда .

В ответ запишем .

. Сторона АС треугольника АВС с тупым углом В равна радиусу описанной около него окружности. Найдите угол В. Ответ дайте в градусах.

По теореме синусов,

Получаем, что . Угол — тупой. Значит, он равен .

. Боковые стороны равнобедренного треугольника равны , основание равно . Найдите радиус описанной окружности этого треугольника.

Углы треугольника не даны. Что ж, выразим его площадь двумя разными способами.

, где — высота треугольника. Ее найти несложно — ведь в равнобедренном треугольнике высота является также и медианой, то есть делит сторону пополам. По теореме Пифагора найдем . Тогда .

Задачи на вписанные и описанные треугольники особенно необходимы тем, кто нацелен на решения задания .