Как начертить 12 угольник в окружности с помощью циркуля

Видео:Построение 10 угольника циркулемСкачать

Как начертить двенадцатиугольник

Умение строить правильные многоугольники необходимо любому специалисту, по роду своей деятельности связанному с черчением или геометрией. Построить двенадцатиугольник с помощью обычных чертежных инструментов можно как минимум тремя способами. Компьютерные же программы позволяют это сделать за несколько минут.Вам понадобится

Первый «классический» способ заключается позволяет обойтись без циркуля. Поставьте на листе точку и проведите через нее произвольную прямую. Точку можно как-нибудь обозначить. Например, это может быть точка О. В одну из сторон отложите от нее отрезок любой длины. Обозначьте его как ОА.

Разделите 360° на 12. Полученную величину в 30° отложите от отрезка ОА, совместив нулевое деление транспортира с точкой О. На полученном луче отложите размер, равный длине отрезка ОА. Таким же образом отложите угол в 30° и от этого нового отрезка. Продолжите построение, откладывая размер угла от каждой новой линии. Соедините конечные точки всех отрезков прямыми.

Гораздо более точное построение можно выполнить с помощью циркуля. Начертите окружность с центром в точке О. Обозначьте на этой окружности какую-либо точку. Например, пусть это будет точка А. Проведите через нее радиус.

Разведите ножки циркуля на длину радиуса окружности. Иголку инструмента поставьте в точку А. На окружности сделайте отметку В. Переставьте циркуль в эту точку и сделайте на окружности еще одну отметку С. Повторяйте операцию до тех пор, пока не разделите окружность на 6 равных частей.

Отметки на окружности соедините отрезками. У вас получился правильный шестиугольник. Каждую его сторону разделите пополам и к полученной точке проведите перпендикуляр. Перпендикуляры необходимо продлить, чтобы они пересекли окружность. У вас получится еще 6 точек.

Гораздо более точное построение можно выполнить с помощью циркуля. Начертите окружность с центром в точке О. Обозначьте на этой окружности какую-либо точку. Например, пусть это будет точка А. Проведите через нее радиус.

Соедините полученные точки с соседними вершинами правильного шестиугольника. У вас получился правильный двенадцатиугольнрик. Лишние линии при необходимости можно убрать.

Построить правильный двенадцатиугольник с помощью циркуля можно и иначе. Начните с построения окружности. Начертите 2 диаметра перпендикулярно друг другу. Если вы сделаете конечные точки каждого центрами новых окружностей того же радиуса, то исходная окружность разделится на 12 равных частей. Вам останется только соединить соседние вершины отрезками.

Правильный двенадцатиугольник в программе AutoCAD строится с помощью команды «Многоугольник», он же polygon. Ее можно ввести в командную строку (латиницей, причем перед командой ставится значок «_»..Перед вами появится окошко, в которое нужно просто ввести число сторон. Соответствующий инструмент можно найти также в панели инструментов на рабочем столе или через вкладку «Рисование» в главном меню.

Программа предложит вам определить способ, по которому вы будете строить двенадцатиугольник. В AutoCAD любой многоугольник можно начертить по длине стороны, центру и радиусу вписанной или описанной окружности. Выберите нужное.

Если вы будете строить двенадцатиугольник по одному из радиусов, укажите центр фигуры. Это можно сделать, задав координаты или отметив нужную точку щелчком мыши. Укажите, радиус какой окружности вам задан, и введите нужное значение.

Видео:Построение 8 угольника циркулемСкачать

Постройте правильный двенадцатиугольник, вписанный в данную окружность.

Видео:Построение 12 угольника циркулемСкачать

Ваш ответ

Видео:КАК РАЗДЕЛИТЬ ОКРУЖНОСТЬ НА 12 РАВНЫХ ЧАСТЕЙ?Скачать

Похожие вопросы

• Все категории
• экономические 43,282
• гуманитарные 33,619
• юридические 17,900
• школьный раздел 607,029
• разное 16,829

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:Геометрия - Построение десятиугольникаСкачать

Как нарисовать 12 угольник в окружности циркулем

Видео:Деление окружности на 3; 6; 12 равных частейСкачать

Как начертить двенадцатиугольник

Умение строить правильные многоугольники необходимо любому специалисту, по роду своей деятельности связанному с черчением или геометрией. Построить двенадцатиугольник с помощью обычных чертежных инструментов можно как минимум тремя способами. Компьютерные же программы позволяют это сделать за несколько минут.Вам понадобится

Первый «классический» способ заключается позволяет обойтись без циркуля. Поставьте на листе точку и проведите через нее произвольную прямую. Точку можно как-нибудь обозначить. Например, это может быть точка О. В одну из сторон отложите от нее отрезок любой длины. Обозначьте его как ОА.

Разделите 360° на 12. Полученную величину в 30° отложите от отрезка ОА, совместив нулевое деление транспортира с точкой О. На полученном луче отложите размер, равный длине отрезка ОА. Таким же образом отложите угол в 30° и от этого нового отрезка. Продолжите построение, откладывая размер угла от каждой новой линии. Соедините конечные точки всех отрезков прямыми.

Гораздо более точное построение можно выполнить с помощью циркуля. Начертите окружность с центром в точке О. Обозначьте на этой окружности какую-либо точку. Например, пусть это будет точка А. Проведите через нее радиус.

Разведите ножки циркуля на длину радиуса окружности. Иголку инструмента поставьте в точку А. На окружности сделайте отметку В. Переставьте циркуль в эту точку и сделайте на окружности еще одну отметку С. Повторяйте операцию до тех пор, пока не разделите окружность на 6 равных частей.

Отметки на окружности соедините отрезками. У вас получился правильный шестиугольник. Каждую его сторону разделите пополам и к полученной точке проведите перпендикуляр. Перпендикуляры необходимо продлить, чтобы они пересекли окружность. У вас получится еще 6 точек.

Гораздо более точное построение можно выполнить с помощью циркуля. Начертите окружность с центром в точке О. Обозначьте на этой окружности какую-либо точку. Например, пусть это будет точка А. Проведите через нее радиус.

Соедините полученные точки с соседними вершинами правильного шестиугольника. У вас получился правильный двенадцатиугольнрик. Лишние линии при необходимости можно убрать.

Построить правильный двенадцатиугольник с помощью циркуля можно и иначе. Начните с построения окружности. Начертите 2 диаметра перпендикулярно друг другу. Если вы сделаете конечные точки каждого центрами новых окружностей того же радиуса, то исходная окружность разделится на 12 равных частей. Вам останется только соединить соседние вершины отрезками.

Правильный двенадцатиугольник в программе AutoCAD строится с помощью команды «Многоугольник», он же polygon. Ее можно ввести в командную строку (латиницей, причем перед командой ставится значок «_»..Перед вами появится окошко, в которое нужно просто ввести число сторон. Соответствующий инструмент можно найти также в панели инструментов на рабочем столе или через вкладку «Рисование» в главном меню.

Программа предложит вам определить способ, по которому вы будете строить двенадцатиугольник. В AutoCAD любой многоугольник можно начертить по длине стороны, центру и радиусу вписанной или описанной окружности. Выберите нужное.

Если вы будете строить двенадцатиугольник по одному из радиусов, укажите центр фигуры. Это можно сделать, задав координаты или отметив нужную точку щелчком мыши. Укажите, радиус какой окружности вам задан, и введите нужное значение.

Видео:Построение девятиугольника циркулем, приближенноеСкачать

Построение правильных многоугольников

Задача 1

Построить правильный шестиугольник, сторона которого равна данному отрезку.

Дано: отрезок DC.

Построить: правильный шестиугольник, сторона которого равна DC.

Решение:

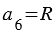
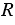
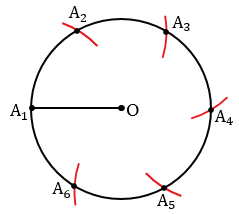
Для решения задачи воспользуемся тем, что сторона шестиугольника равна радиусу описанной около него окружности, т.е. (смотри формулу для вычисления стороны правильного многоугольника), где — радиус окружности описанной около правильного многоугольника. Нам нужно построить правильный шестиугольник со стороной DC, поэтому с помощью циркуля измеряем отрезок DC и строим окружность радиуса DC, и отмечаем на ней произвольную точку А₁, центр окружности обозначаем буквой О.

Затем не меняя раствора циркуля, построим на этой окружности точки А₂, А₃, А₄, А₅, А₆, так, чтобы выполнялись равенства

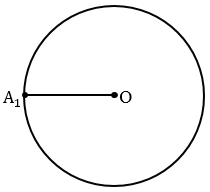
А₁А₂ = А₂А₃ = А₃А₄ = А₄А₅ = А₅А₆ = DC (т.е. сначала строим окружность радиуса DC с центром в точке А₁ (всю окружность строить необязательно, смотри выделенное красным), данная окружность пересечет окружность с центром О в точке А₂, далее аналогично строим окружность радиуса DC с центром в точке А₂, она пересечет окружность с центром О в точке А₃ и т.д.).

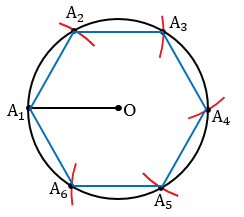
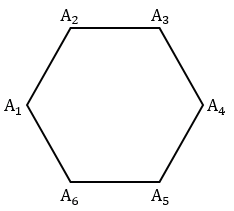
Теперь соединяя последовательно построенные точки отрезками, получим искомый правильный шестиугольник А₁А₂А₃А₄А₅А₆.

Задача 2

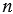
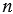
Дан правильный -угольник. Построить правильный 2-угольник.

Дано: правильный 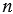-угольник А₁А₂А₃. А_n.

Построить: правильный 2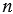-угольник.

Решение:

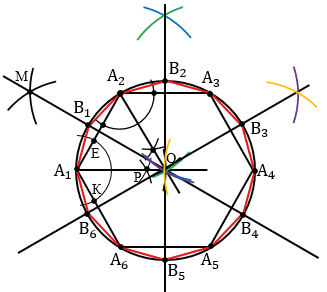
Пусть, например, нам дан шестиугольник А₁А₂А₃А₄А₅А₆, значит, построить нужно двенадцатиугольник.

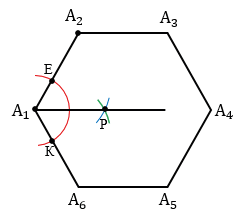
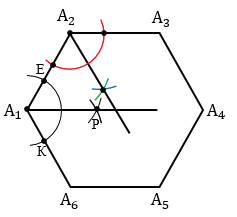
Сначала опишем около данного шестиугольника А₁А₂А₃А₄А₅А₆ окружность. Для этого построим биссектрисы углов А₁ и А₂. Чтобы построить биссектрису угла А₁, строим окружность произвольного радиуса с центром в точке А₁ (полностью окружность строить необязательно, смотри выделенное красным цветом), данная окружность пересечет стороны А₁А₂ и А₁А₆ угла А₁ в точках Е и К. Затем строим две окружности с центрами в точках Е и К радиуса ЕК (полностью окружности строить необязательно, смотри выделенное синим и зеленым цветом), данные окружности пересекутся в точке Р. Далее проводим луч А₁Р, который и будет биссектрисой угла А₁.

Аналогично строим биссектрису угла А₂.

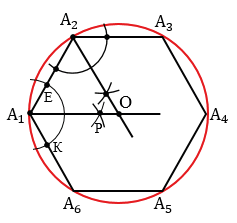
Точку пересечения биссектрис углов А₁ и А₂ обозначаем буквой О и строим окружность радиуса ОА₁ с центром О (окружность описанная около А₁А₂А₃А₄А₅А₆).

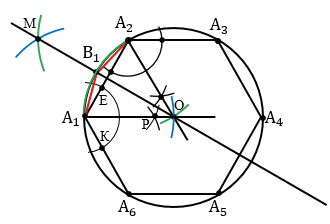
Далее нужно каждую из дуг А₁А₂, А₂А₃, А₃А₄, А₄А₅, А₅А₆, А₆А₁ разделить пополам. Чтобы разделить дугу А₁А₂ пополам, построим серединный перпендикуляр к отрезку А₁А₂. Для этого строим две окружности с центрами в точках А₁ и А₂ радиуса А₁А₂ (полностью окружность строить необязательно, смотри выделенное красным цветом). Данные окружности пересекутся в двух точках, одну обозначим буквой М, а другая совпадет с точкой О, т.к. у шестиугольника сторона равна радиусу (с другими многоугольниками совпадения с точкой О не будет) . Затем проводим прямую МО, данная прямая пересечет дугу А₁А₂ в точке В₁, которая и разделит дугу А₁А₂ пополам. Далее точку В₁ соединяем с концами А₁ и А₂ дуги А₁А₂.

Аналогично находим точки В₂, В₃. Точки В₄, В₅, В₆ в данном случае строить необязательно, они получаются автоматически при построении точек В₁, В₂, В₃, т.к. шестиугольник симметричная фигура.

Мы выполняли построения на примере правильного шестиугольника, если мы имеем произвольный правильный 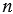-угольник, то все построения выполняются аналогично.

Применяя указанный способ, можно с помощью циркуля и линейки построить целый ряд правильных многоугольников, если построен один из них. Например, построив правильный треугольник и пользуясь результатом задачи 2, можно построить правильный шестиугольник, затем правильный двенадцатиугольник и вообще 2 k -угольник, где 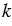— любое целое число, больше двух.

Замечание

Не все правильные многоугольники можно построить с помощью циркуля и линейки. Доказано, например, что правильный семиугольник не может быть построен при помощи циркуля и линейки.

Поделись с друзьями в социальных сетях:

Видео:Построение пятиугольника циркулемСкачать

Как начертить двенадцатиугольник в окружности

Деление окружности на равные части и по­строение правильных вписанных многоуголь­ников можно выполнить как циркулем, так и с помощью угольников и рейсшины.

Деление окружности на четыре равные части и построение пра­вильного вписанного четырех­угольника. Две взаимно перпендикулярные центровые линии делят окружность на четыре равные части (рис. 115, а). Соединив точки пе­ресечения этих линий с окружностью прямы­ми, получают правильный вписанный четырех­угольник.

Деление окружности на восемь равных частей и построение пра­вильного вписанного восьмиуголь­ника. Две взаимно перпендикулярные линии, проведенные под углом 45° к центровым ли­ниям с помощью угольника с углами 45, 45 и 90° и рейсшины (рис. 115, б), вместе с центро­выми линиями разделят окружность на восемь равных частей.

Деление окружности на восемь равных час­тей можно выполнить циркулем. Для этого из точек 1 и 3 (точки пересечения центровых линий с окружностью) произвольным радиусом делаются засечки до взаимного пересечения, тем же радиусом делают две засечки из точек 3 и 5 (рис. 115, в). Через точки пересечения засечек и центр окружности проводят прямые линии до пересечения с окружностью в точках 2, 4, 6, 8.

Если полученные восемь точек соединить последовательно прямыми линиями, то полу­чится правильный вписанный восьмиугольник (рис. 115, в).

Деление окружности на три рав­ные части и построение правиль­ного вписанного треугольника вы­полняют с помощью циркуля или угольника с углами 30, 60 и 90° и рейсшины.

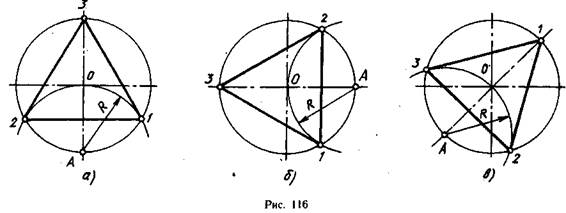
При делении окружности циркулем на три равные части из любой точки окружности, на­пример из точки Л пересечения центровых ли­ний с окружностью (рис. 116, а и б), проводят дугу радиусом R, равным радиусу данной ок­ружности, получают точки 1 и 2. Третья точка деления (точка 3) будет находиться на про­тивоположном конце диаметра, проходящего через точку Л. Последовательно соединив точ­ки 1, 2 и 3, получают правильный вписанный треугольник. При построении правильного впи­санного треугольника, если задана одна из его вершин, например точка 1, находят точку А. Для этого через заданную точку 1 проводят диаметр (рис. 116, в). Точка А будет находить­ся на противоположном конце этого диаметра. Затем проводят дугу радиусом R равным ра­диусу данной окружности, получают точки 2 и 3.

При делении окружности на три равные час­ти с помощью угольника и рейсшины через точку 1 под углом 60° проводят две прямые линии до пересечения с окружностью в точках 2 и 3 (рис. 117, а, б), точки 2 и 3 соединяют и получают правильный вписанный треугольник (рис. 117, в).

Деление окружности на шесть равных частей и построение пра­вильного вписанного шестиуголь­ника выполняют с помощью угольника с уг­лами 30, 60 и 90° и рейсшины или циркуля. При делении окружности на шесть равных частей циркулем из двух концов одного диа­метра радиусом, равным радиусу данной окруж­ности, проводят дуги до пересечения с окруж­ностью в точках 2, 6 и 3, 5 (рис. 118). Последовательно соединив полученные точки, полу­чают правильный вписанный шестиугольник. Деление окружности на шесть равных час-1ен и построение правильного вписанного шестиугольника с помощью угольника и рейс­шины показано на рис. 119 и 120. Деление окружности на двенад­цать равных частей и построение правильного вписанного двенад­цатиугольника выполняют с помощью угольника с углами 30, 60 и 90° и рейсшины или циркуля.

При делении окружности циркулем из четы­рех концов двух взаимно перпендикулярных диаметров окружности проводят радиусом, рав­ным радиусу данной окружности, дуги до пере­сечения с окружностью (рис. 121). Соединив по­лученные точки, получают двенадцатиугольник.

При построении двенадцатиугольника с по­мощью угольника и рейсшины точки деления строят, как показано на рис. 119 и 120.

Деление окружности на пять и десять равных частей и построе­ние правильного вписанного пяти­угольника и десятиугольника пока­зано на рис. 122.

Половину любого диаметра (радиус) делят пополам (рис. 122, а), получают точку А. Из точки А, как из центра, проводят дугу радиу­сом, равным расстоянию от точки А до точки 1, до пересечения со второй половиной этого диаметра, в точке В (рис. 122, б). Отрезок 1В равен хорде, стягивающей дугу, длина которой равна 1 /₅ длины окружности. Делая засечки на окружности (рис. 122, в) радиусом R, равным отрезку 1В, делят окруж­ность на пять равных частей. Начальную точку 1 выбирают в зависимости от расположения пятиугольника. Из точки / строят точки 2 и 5 (рис. 122, в), затем из точки 2 строят точку 3, а из точки 5 строят точку 4. Расстояние от точки 3 до точки 4 проверяют циркулем; если расстояние между точками 3 и 4 равно отрезку 1В, то построения были выполнены точно. Нельзя выполнять засечки последовательно, в одну сторону, так как происходит набегание ошибок и последняя сторона пятиугольника получается перекошенной. Последовательно соединив найденные точки, получают пяти­угольник (рис. 122, г).

Деление окружности на десять равных час­тей выполняют аналогично делению окруж­ности на пять равных частей (рис. 122), но сначала делят окружность на пять частей, на­чиная построение из точки /, а затем из точ­ки 6, находящейся на противоположном конце диаметра (рис. 123, а). Соединив последова­тельно все точки, получают правильный впи­санный десятиугольник (рис. 123, б).

Деление окружности на семь и четырнадцать равных частей и по­строение правильного вписанного семиугольника и четырнадцатиугольника показано на рис. 124 и 125.

Из любой точки окружности, например точ­ки Л, радиусом заданной окружности проводят дугу (рис. 124, а) до пересечения с окруж­ностью в точках В и D. Соединим точки В и D прямой. Половина полученного отрезка (в данном случае отрезок ВС) будет равна хорде, которая стягивает дугу, составляющую 1 /₇ дли­ны окружности. Радиусом, равным отрезку ВС, делают засечки на окружности в последова­тельности, показанной на рис. 124, б. Соединив последовательно все точки, получают правиль­ный вписанный семиугольник (рис. 124, в).

Деление окружности на четырнадцать рав­ных частей выполняется делением окружности на семь равных частей два раза от двух точек (рис. 125, а).

Сначала окружность делится на семь рав­ных частей от точки /, затем то же построение выполняется от точки 8. Построенные точки соединяют последовательно прямыми линиями и получают правильный вписанный четырна-дцатиугольник (рис. 125, б).

СОПРЯЖЕНИЯ

Рассматривая детали, видим, что в их конст­рукции часто одна поверхность переходит в другую. Обычно эти переходы делают плав­ными, что повышает прочность деталей и де­лает их более удобными в работе. На чертеже поверхности изображаются линиями, которые также плавно переходят одна в другую.

На рис. 126, а изображена деталь, в которой плавные переходы одних плоскостей в другие представляют собой цилиндрические поверхнос­ти. На чертеже (рис. 126, б) эти плоскости изо­бражены прямыми линиями, а цилиндрические поверхности — дугами окружностей. Плавные переходы от одной прямой к другой в этих случаях выполняются дугой заданного радиуса.

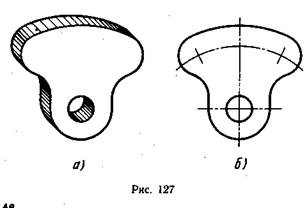
Плавный переход одной цилиндрической поверхности в другую может являться цилинд­рической поверхностью (рис. 127, а). На черте­же эти цилиндрические поверхности изобра­жены дугами окружностей, (рис. 127, б). В этом случае плавный переход одной дуги окруж­ности в другую осуществляется дугой окруж­ности заданного радиуса.

На рис. 126, а и 127, а рассмотрены простей­шие примеры плавных переходов поверхностей. В чертежах более сложных деталей плавные переходы между поверхностями изображают­ся различными сочетаниями прямых, окруж­ностей и их дуг. Вариантов таких сочетаний может быть много, но их объединяет од­но — плавность перехода. Такой плавный пе­реход одной линии (поверхности) в другую ли­нию (поверхность) называют сопряжени­ем. При построении сопряжения необходимо определить границу, где кончается одна линия и начинается другая, т. е. найти на чертеже точку перехода, которая называется точкой сопряжения или точкой касания.

Задачи на сопряжения условно можно раз­делить на три группы.

Первая группа задачвключает в себя зада­чи на построение сопряжений, где участвуют прямые линии. Это может быть непосредствен­ное касание прямой и окружности, сопряжение двух прямых дугой заданного радиуса, а также проведение касательной прямой к двум окружностям.

Построение окружности, каса­тельной к прямой, связано с нахождени­ем точки касания и центра окружности.

Задана горизонтальная прямая АВ, требует­ся построить окружность радиусом R, касательную к данной прямой (рис. 128). Точка касания выбирается произвольно. Так как точка касания не задана, то окружность ра­диуса R может коснуться данной прямой в любой точке. Таких окружностей можно про­вести множество. Центры этих окружностей (O₁, О₂ и т. д.) будут находиться на одина­ковом расстоянии от заданной прямой, т. е. на линии, расположенной параллельно заданной прямой АВ на расстоянии, равном радиусу заданной окружности (рис. 128). Назовем эту линию линией центров. Проведем линию центров параллельно прямой АВ на расстоя­нии R. Так как центр касательной окруж­ности не задан, возьмем любую точку на линии центров, например точку О. Прежде чем про­водить касательную окружность, следует опре­делить точку касания. Точка касания будет лежать на перпендикуляре, опущенном из точ­ки О на прямую АВ. В пересечении перпендику­ляра с прямой АВ получим точку К, которая будет точкой касания. Из центра О радиусом R от точки К проведем окружность. Задача решена.

В детали, которая изображена на рис. 129, а, пластина плавно переходит в цилиндр. При выполнении чертежа этой детали необходимо построить плавный переход прямой в окруж­ность.

Задача аналогична предыдущей, но до­полнена условием, что точка касания задана, так как задан размер А (рис. 129, б), который определяет величину прямолинейного участка.

Отложив размер Л, находят точку касания (точку /С), затем из точки К восставляют пер­пендикуляр, на котором откладывают радиус R заданной окружности, и находят центр ок­ружности (точку О). При обводке сначала от точки касания проводится дуга заданного ра­диуса, а потом — прямая.

Из сказанного следует:

1) центр окружности, касательной к прямой, лежит на прямой (линия центров), проведенной параллельно заданной прямой, на расстоянии, равном радиусу данной окружности;

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Сдача сессии и защита диплома — страшная бессонница, которая потом кажется страшным сном. 8738 — | 7137 — или читать все.

188.64.173.93 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Видео:Построение шестнадцатиугольника циркулемСкачать

Скажите пожалуйста как нарисовать двадцатиугольник или отправьте сылку сайта

Возьмите циркуль и начертите окружность. Затем выберите на этой окружности произвольную точку (назовем ее А). Поставьте циркуль в эту точку и сделайте на окружности засечку (точка В), расстояние до которой будет равно радиусу этой окружности. Переставьте циркуль в полученную точку и вновь отложите на окружности то же расстояние (равное отрезку АВ), а затем повторите операцию еще три раза. В итоге на вашей окружности должны появиться 6 точек (А, В, С, D, E и F), равноудаленных друг от друга. Соедините все полученные точки отрезками, а затем отметьте середины каждой из сторон построенного вами шестиугольника АВСDEF. После этого проведите срединные перпендикуляры к каждому из шести отрезков, продляя их до пересечения с окружностью. Вы получите шесть новых точек на окружности – недостающие вершины 12-угольника. Для завершения построения эти точки нужно будет соединить с ближайшими к ним вершинами шестиугольника ABCDEF. В результате вы получите правильный многоугольник с двенадцатью равными углами и сторонами. Есть еще один способ построения правильного 12-угольника. После проведения окружности и обозначения на ней произвольной точки (А), проведите из этой точки диаметр окружности (назовем его АD). Затем начертите две окружности того же радиуса, что и исходная, с центрами в концах диаметра (А и D). Каждая из этих двух окружностей пересечет исходную в двух нужных вам точках. Затем проведите еще один диаметр исходной окружности, строго перпендикулярный первому (назовем его МР), и из обоих концов диаметра (М и Р) снова проведите окружности того же радиуса. Каждая из них пересечет исходную окружность еще в двух точках. В итоге вы получите 12 точек: A, D, M, P, а также по 2 точки пересечения четырех новых окружностей с исходной. Теперь для завершения построения 12-угольника вам останется только соединить эти точки отрезками.

Видео:Деление окружности на n- равные частиСкачать

Техническое черчение

Основы черчения

Строительное

Машиностроительное

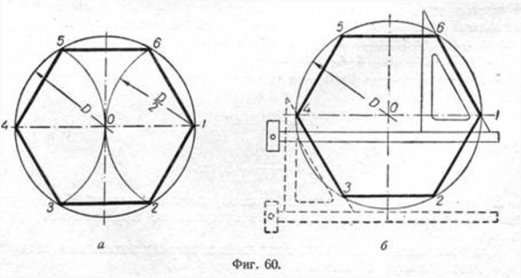
Построение вписанного в окружность правильного шестиуголь­ника. Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения доста­точно разделить окружность на шесть равных частей и соединить най­денные точки между собой (фиг. 60, а).

Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг. 60, б), строим стороны 1 —6, 4—3, 4—5 и 7—2, после чего прово­дим стороны 5—6 и 3—2.

Построение вписанного в окружность равностороннего треуголь­ника. Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного цир­куля.

Рассмотрим два способа построения вписанного в окружность рав­ностороннего треугольника.

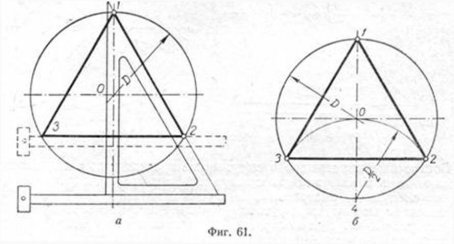
Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, прове­дённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0—1—2 равен 30°, то для нахождения стороны

1—2 достаточно построить по точке 1 и стороне 0—1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1—2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2—3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 прово­дим прямую, которая определит третью вершину треугольника.

Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вер­шины через одну, то получится равносторонний треугольник.

Для построения треугольника (фиг. 61, б) намечаем на диаметре вершину—точку 1 и проводим диаметральную линию 1—4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окруж­ностью в точках 3 и 2. Полученные точки будут двумя другими вер­шинами искомого треугольника.

Построение квадрата, вписанного в окружность. Это построение можно выполнить при помощи угольника и циркуля.

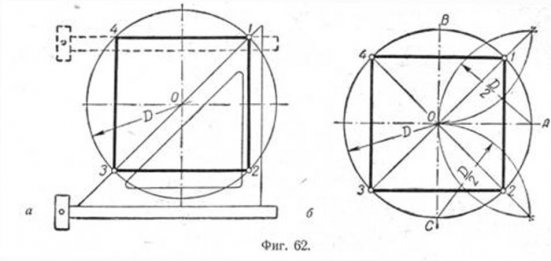
Первый способ основан на том, что диагонали квадрата пере­секаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные сто­роны квадрата 4—1 и 3—2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1—2 и 4—3.

Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра (фиг. 62, б). Намечаем на концах двух взаимно перпендикулярных диа­метров точки А, В и С и из них радиусом у описываем дуги до вза­имного их пересечения.

Далее через точки пересечения дуг проводим вспомогательные пря­мые, отмеченные на фигуре сплошными линиями. Точки их пересече­ния с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.

Построение вписанного в окружность правильного пятиугольника.

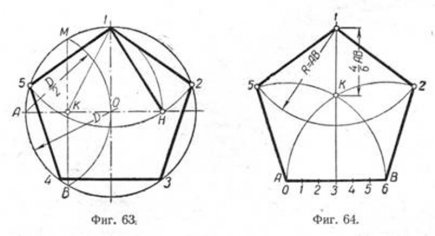
Чтобы вписать в окружность правильный пятиугольник (фиг. 63), про­изводим следующие построения.

Намечаем на окружности точку 1 и принимаем её за одну из вер­шин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точ­ках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вер­шины 3 и 4. Найденные точки последовательно соединяем между собой.

Построение правильного пятиугольника по данной его стороне.

Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую.

Далее от точки К на этой прямой откладываем отрезок, равный 4/6 AB.

Получим точку 1—вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведён­ными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.

Построение вписанного в окружность правильного семиугольника.

Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг. 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиу­сом, равным диаметру окружности D, описываем дугу до пересечения с про­должением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, прово­дим из полюса F через чётные деления вертикального диаметра лучи, пересече­ние которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем после­довательно между собой. Семиугольник может быть построен путём проведе­ния лучей из полюса F и через нечётные деления вертикального диаметра.

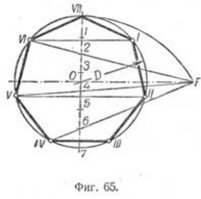
Приведённый способ годен для построения правильных многоуголь­ников с любым числом сторон.

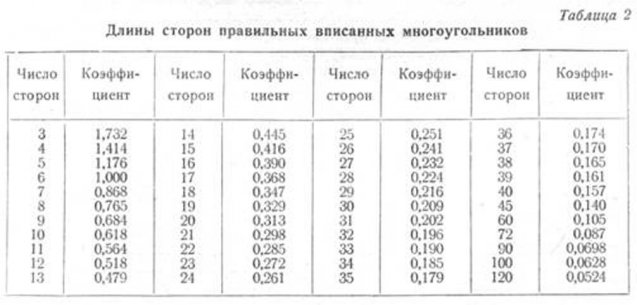
Деление окружности на любое число равных частей можно произ­водить также, пользуясь данными табл. 2, в которой приведены коэф­фициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.

В первой колонке этой таблицы указаны числа сторон правильного вписанного многоугольника, а во второй—коэффициенты.

Длина стороны заданного многоугольника получится от умножения радиуса данной окружности на коэффициент, соответствующий числу сторон этого многоугольника.

Видео:Деление окружности на 3, 4, 5, 6 и 7 равных частейСкачать

ПОСТРОЕНИЕ ПРАВИЛЬНЫХ ВПИСАННЫХ МНОГОУГОЛЬНИКОВ.

Деление окружности на равные части и по­строение правильных вписанных многоуголь­ников можно выполнить как циркулем, так и с помощью угольников и рейсшины.

Деление окружности на четыре равные части и построение пра­вильного вписанного четырех­угольника. Две взаимно перпендикулярные центровые линии делят окружность на четыре равные части (рис. 115, а). Соединив точки пе­ресечения этих линий с окружностью прямы­ми, получают правильный вписанный четырех­угольник.

Деление окружности на восемь равных частей и построение пра­вильного вписанного восьмиуголь­ника. Две взаимно перпендикулярные линии, проведенные под углом 45° к центровым ли­ниям с помощью угольника с углами 45, 45 и 90° и рейсшины (рис. 115, б), вместе с центро­выми линиями разделят окружность на восемь равных частей.

Деление окружности на восемь равных час­тей можно выполнить циркулем. Для этого из точек 1 и 3 (точки пересечения центровых линий с окружностью) произвольным радиусом делаются засечки до взаимного пересечения, тем же радиусом делают две засечки из точек 3 и 5 (рис. 115, в). Через точки пересечения засечек и центр окружности проводят прямые линии до пересечения с окружностью в точках 2, 4, 6, 8.

Если полученные восемь точек соединить последовательно прямыми линиями, то полу­чится правильный вписанный восьмиугольник (рис. 115, в).

Деление окружности на три рав­ные части и построение правиль­ного вписанного треугольника вы­полняют с помощью циркуля или угольника с углами 30, 60 и 90° и рейсшины.

При делении окружности циркулем на три равные части из любой точки окружности, на­пример из точки Л пересечения центровых ли­ний с окружностью (рис. 116, а и б), проводят дугу радиусом R, равным радиусу данной ок­ружности, получают точки 1 и 2. Третья точка деления (точка 3) будет находиться на про­тивоположном конце диаметра, проходящего через точку Л. Последовательно соединив точ­ки 1, 2 и 3, получают правильный вписанный треугольник. При построении правильного впи­санного треугольника, если задана одна из его вершин, например точка 1, находят точку А. Для этого через заданную точку 1 проводят диаметр (рис. 116, в). Точка А будет находить­ся на противоположном конце этого диаметра. Затем проводят дугу радиусом R равным ра­диусу данной окружности, получают точки 2 и 3.

При делении окружности на три равные час­ти с помощью угольника и рейсшины через точку 1 под углом 60° проводят две прямые линии до пересечения с окружностью в точках 2 и 3 (рис. 117, а, б), точки 2 и 3 соединяют и получают правильный вписанный треугольник (рис. 117, в).

Деление окружности на шесть равных частей и построение пра­вильного вписанного шестиуголь­ника выполняют с помощью угольника с уг­лами 30, 60 и 90° и рейсшины или циркуля. При делении окружности на шесть равных частей циркулем из двух концов одного диа­метра радиусом, равным радиусу данной окруж­ности, проводят дуги до пересечения с окруж­ностью в точках 2, 6 и 3, 5 (рис. 118). Последовательно соединив полученные точки, полу­чают правильный вписанный шестиугольник. Деление окружности на шесть равных час-1ен и построение правильного вписанного шестиугольника с помощью угольника и рейс­шины показано на рис. 119 и 120. Деление окружности на двенад­цать равных частей и построение правильного вписанного двенад­цатиугольника выполняют с помощью угольника с углами 30, 60 и 90° и рейсшины или циркуля.

При делении окружности циркулем из четы­рех концов двух взаимно перпендикулярных диаметров окружности проводят радиусом, рав­ным радиусу данной окружности, дуги до пере­сечения с окружностью (рис. 121). Соединив по­лученные точки, получают двенадцатиугольник.

При построении двенадцатиугольника с по­мощью угольника и рейсшины точки деления строят, как показано на рис. 119 и 120.

Деление окружности на пять и десять равных частей и построе­ние правильного вписанного пяти­угольника и десятиугольника пока­зано на рис. 122.

Половину любого диаметра (радиус) делят пополам (рис. 122, а), получают точку А. Из точки А, как из центра, проводят дугу радиу­сом, равным расстоянию от точки А до точки 1, до пересечения со второй половиной этого диаметра, в точке В (рис. 122, б). Отрезок 1В равен хорде, стягивающей дугу, длина которой равна 1 /₅ длины окружности. Делая засечки на окружности (рис. 122, в) радиусом R, равным отрезку 1В, делят окруж­ность на пять равных частей. Начальную точку 1 выбирают в зависимости от расположения пятиугольника. Из точки / строят точки 2 и 5 (рис. 122, в), затем из точки 2 строят точку 3, а из точки 5 строят точку 4. Расстояние от точки 3 до точки 4 проверяют циркулем; если расстояние между точками 3 и 4 равно отрезку 1В, то построения были выполнены точно. Нельзя выполнять засечки последовательно, в одну сторону, так как происходит набегание ошибок и последняя сторона пятиугольника получается перекошенной. Последовательно соединив найденные точки, получают пяти­угольник (рис. 122, г).

Деление окружности на десять равных час­тей выполняют аналогично делению окруж­ности на пять равных частей (рис. 122), но сначала делят окружность на пять частей, на­чиная построение из точки /, а затем из точ­ки 6, находящейся на противоположном конце диаметра (рис. 123, а). Соединив последова­тельно все точки, получают правильный впи­санный десятиугольник (рис. 123, б).

Деление окружности на семь и четырнадцать равных частей и по­строение правильного вписанного семиугольника и четырнадцатиугольника показано на рис. 124 и 125.

Из любой точки окружности, например точ­ки Л, радиусом заданной окружности проводят дугу (рис. 124, а) до пересечения с окруж­ностью в точках В и D. Соединим точки В и D прямой. Половина полученного отрезка (в данном случае отрезок ВС) будет равна хорде, которая стягивает дугу, составляющую 1 /₇ дли­ны окружности. Радиусом, равным отрезку ВС, делают засечки на окружности в последова­тельности, показанной на рис. 124, б. Соединив последовательно все точки, получают правиль­ный вписанный семиугольник (рис. 124, в).

Деление окружности на четырнадцать рав­ных частей выполняется делением окружности на семь равных частей два раза от двух точек (рис. 125, а).

Сначала окружность делится на семь рав­ных частей от точки /, затем то же построение выполняется от точки 8. Построенные точки соединяют последовательно прямыми линиями и получают правильный вписанный четырна-дцатиугольник (рис. 125, б).

СОПРЯЖЕНИЯ

Рассматривая детали, видим, что в их конст­рукции часто одна поверхность переходит в другую. Обычно эти переходы делают плав­ными, что повышает прочность деталей и де­лает их более удобными в работе. На чертеже поверхности изображаются линиями, которые также плавно переходят одна в другую.

На рис. 126, а изображена деталь, в которой плавные переходы одних плоскостей в другие представляют собой цилиндрические поверхнос­ти. На чертеже (рис. 126, б) эти плоскости изо­бражены прямыми линиями, а цилиндрические поверхности — дугами окружностей. Плавные переходы от одной прямой к другой в этих случаях выполняются дугой заданного радиуса.

Плавный переход одной цилиндрической поверхности в другую может являться цилинд­рической поверхностью (рис. 127, а). На черте­же эти цилиндрические поверхности изобра­жены дугами окружностей, (рис. 127, б). В этом случае плавный переход одной дуги окруж­ности в другую осуществляется дугой окруж­ности заданного радиуса.

На рис. 126, а и 127, а рассмотрены простей­шие примеры плавных переходов поверхностей. В чертежах более сложных деталей плавные переходы между поверхностями изображают­ся различными сочетаниями прямых, окруж­ностей и их дуг. Вариантов таких сочетаний может быть много, но их объединяет од­но — плавность перехода. Такой плавный пе­реход одной линии (поверхности) в другую ли­нию (поверхность) называют сопряжени­ем. При построении сопряжения необходимо определить границу, где кончается одна линия и начинается другая, т. е. найти на чертеже точку перехода, которая называется точкой сопряжения или точкой касания.

Задачи на сопряжения условно можно раз­делить на три группы.

Первая группа задачвключает в себя зада­чи на построение сопряжений, где участвуют прямые линии. Это может быть непосредствен­ное касание прямой и окружности, сопряжение двух прямых дугой заданного радиуса, а также проведение касательной прямой к двум окружностям.

Построение окружности, каса­тельной к прямой, связано с нахождени­ем точки касания и центра окружности.

Задана горизонтальная прямая АВ, требует­ся построить окружность радиусом R, касательную к данной прямой (рис. 128). Точка касания выбирается произвольно. Так как точка касания не задана, то окружность ра­диуса R может коснуться данной прямой в любой точке. Таких окружностей можно про­вести множество. Центры этих окружностей (O₁, О₂ и т. д.) будут находиться на одина­ковом расстоянии от заданной прямой, т. е. на линии, расположенной параллельно заданной прямой АВ на расстоянии, равном радиусу заданной окружности (рис. 128). Назовем эту линию линией центров. Проведем линию центров параллельно прямой АВ на расстоя­нии R. Так как центр касательной окруж­ности не задан, возьмем любую точку на линии центров, например точку О. Прежде чем про­водить касательную окружность, следует опре­делить точку касания. Точка касания будет лежать на перпендикуляре, опущенном из точ­ки О на прямую АВ. В пересечении перпендику­ляра с прямой АВ получим точку К, которая будет точкой касания. Из центра О радиусом R от точки К проведем окружность. Задача решена.

В детали, которая изображена на рис. 129, а, пластина плавно переходит в цилиндр. При выполнении чертежа этой детали необходимо построить плавный переход прямой в окруж­ность.

Задача аналогична предыдущей, но до­полнена условием, что точка касания задана, так как задан размер А (рис. 129, б), который определяет величину прямолинейного участка.

Отложив размер Л, находят точку касания (точку /С), затем из точки К восставляют пер­пендикуляр, на котором откладывают радиус R заданной окружности, и находят центр ок­ружности (точку О). При обводке сначала от точки касания проводится дуга заданного ра­диуса, а потом — прямая.

Из сказанного следует:

1) центр окружности, касательной к прямой, лежит на прямой (линия центров), проведенной параллельно заданной прямой, на расстоянии, равном радиусу данной окружности;

Не нашли то, что искали? Воспользуйтесь поиском:

Видео:ПОСТРОИТЬ ПРАВИЛЬНЫЙ ПЯТИУГОЛЬНИК [construction a regular pentagon]Скачать

Пятиугольник

Здравствуйте коллеги.
Сегодня построим правильный пятиугольник в окружности, попробуем начертить циркулем и линейкой фигуру.

Рисунки художников очень тесно связаны с черчением и геометрией. Если мы задумали какую-то композицию, а в ней есть геометрические фигуры, то нам необходимо знать, как изобразить предмет, что бы он не выглядел смешно, и что бы вы не выглядели дилетантом и смогли нарисовать пятиконечную звезду циркулем или в фотошопе. От этого зависит ваш авторитет художника, а значит и заказы.

Построение правильного пятиугольника не так часто встречается в рисунке, но все же есть моменты, когда нам это необходимо.

Например, нам нужно нарисовать пятиконечную звезду (пентаграмму) для картины о Советском прошлом или о настоящем Китая. Правда для этого нужно уметь создать рисунок звезды в перспективе. Это посмотрите в другом уроке.

Мы попробуем нарисовать звезду в фотошопе фронтально. Точно так же вы сможете нарисовать фигуру карандашом на бумаге. Всего лишь с помощью таких инструментов:

Как правильно нарисовать звезду, что бы она выглядела ровно и красиво, сразу не ответишь. Количество углов не четное, поэтому просто разделить окружность на равные части циркулем или линейкой не получится.

Что бы вписанный пятиугольник в окружность был пропорциональный, нам необходимо точно вычислить одну из сторон, а затем отложить этот отрезок пять раз на теле овала.

Видео:Построение 7 угольника циркулем, приближенноеСкачать

Как выглядит пятиугольник и звезда

Внизу на фото разберем, как нарисовать звезду поэтапно.
Для начала рисуем окружность с центром О.

Дальше отложим отрезок OA равный радиусу и разделим его пополам точкой B, как показано на фото внизу.

Теперь от точки В до точки С проведем прямую.

Отложим расстояние отрезка ВС на диаметральной линии окружности. Для этого можно воспользоваться циркулем. Таким образом у нас появилась точка D.

И отрезок DB. Картинка внизу.

Дальше, проведя линию от точки D к точке С, Мы получи длину равную стороне пятиугольника.

Дальше этот отрезок можно отложить на окружности. У нас появилась точка Е. Смотрим фото ниже.

Итак, одна из сторон пятиугольника у нас есть, это линия ЕС.

Такие же отрезки наносим на всей части круга. Смотрим картинку.

На этом построение правильного пятиугольника можно закончить. Что бы нарисовать звезду нужно просто соединить углы через один.

Нарисовать пятиконечную звезду циркулем можно так же, как и на нашем уроке в программе Photoshop, весь процесс такой же, только вместо программы графического редактора используем инструменты для черчения.

Так же можно посмотреть уроки построения шестиугольника, разделение на восемь частей, деление круга на семь частей, десять равных частей.

🎬 Видео

Построение пятиугольника циркулем и линейкойСкачать

Деление окружности на равные части с помощью циркуляСкачать

Геометрия - Построение восьмиугольникаСкачать

1 2 2 деление окружности на 5 равных частейСкачать

Деление окружности на равные части. Урок 6. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Построение 12 угольника циркулем на деревянной поверхностиСкачать

Деление окружности на пять равных частей. Урок 7. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать