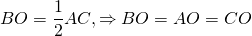Как медиана делит угол треугольника

Определение медианы

Медиана треугольника — это отрезок, который соединяет вершину треугольника с
серединой противоположной стороны. Медиана делит противолежащую сторону пополам.
Основание медианы — это точка пересечения медианы со стороной треугольника.

На рисунке 1 изображены три медианы, делящие каждая свою противолежащую
сторону пополам. Медианы BF, AH, CE соответственно делят пополам свои
противолежащие стороны AC, CB, AB.

Видео:7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

Медиана делит угол треугольника

Видео:🔥 Свойства МЕДИАНЫ #shortsСкачать

Медиана угла

Определение медианы

Медиана треугольника — это отрезок, который соединяет вершину треугольника с
серединой противоположной стороны. Медиана делит противолежащую сторону пополам.
Основание медианы — это точка пересечения медианы со стороной треугольника.

На рисунке 1 изображены три медианы, делящие каждая свою противолежащую
сторону пополам. Медианы BF, AH, CE соответственно делят пополам свои
противолежащие стороны AC, CB, AB.

Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Определение и свойства медианы треугольника

В данной статье мы рассмотрим определение медианы треугольника, перечислим ее свойства, а также разберем примеры решения задач для закрепления теоретического материала.

Видео:Сумма углов треугольника. Геометрия 7 класс | МатематикаСкачать

Определение медианы треугольника

Медиана – это отрезок, соединяющий вершину треугольника с серединой стороны, расположенной напротив данной вершины.

Основание медианы – точка пересечения медианы со стороной треугольника, другими словами, середина этой стороны (точка F).

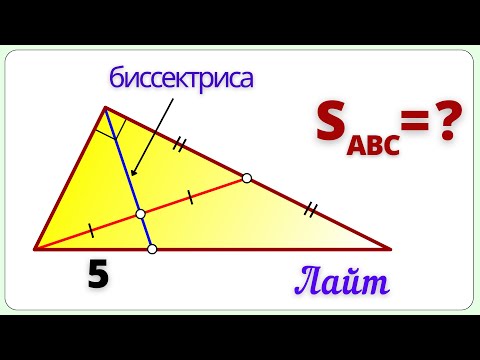
Видео:Биссектриса прямого угла делит медиану пополам! Найти площадь треугольника.Скачать

Свойства медианы

Свойство 1 (основное)

Т.к. в треугольнике три вершины и три стороны, то и медиан, соответственно, тоже три. Все они пересекаются в одной точке (O), которая называется центроидом или центром тяжести треугольника.

В точке пересечения медиан каждая из них делится в отношении 2:1, считая от вершины. Т.е.:

Свойство 2

Медиана делит треугольник на 2 равновеликих (равных по площади) треугольника.

Свойство 3

Три медианы делят треугольник на 6 равновеликих треугольников.

Свойство 4

Наименьшая медиана соответствует большей стороне треугольника, и наоборот.

• AC – самая длинная сторона, следовательно, медиана BF – самая короткая.
• AB – самая короткая сторона, следовательно, медиана CD – самая длинная.

Свойство 5

Допустим, известны все стороны треугольника (примем их за a, b и c).

Длину медианы m_a, проведенную к стороне a, можно найти по формуле:

Видео:Геометрия Медиана, проведенная к гипотенузе прямоугольного треугольника, равна m и делит прямой уголСкачать

Примеры задач

Задание 1
Площадь одной из фигур, образованной в результате пересечения трех медиан в треугольнике, равняется 5 см 2 . Найдите площадь треугольника.

Решение
Согласно свойству 3, рассмотренному выше, в результате пересечения трех медиан образуются 6 треугольников, равных по площади. Следовательно:
S_△ = 5 см 2 ⋅ 6 = 30 см 2 .

Задание 2
Стороны треугольника равны 6, 8 и 10 см. Найдите медиану, проведенную к стороне с длиной 6 см.

Решение
Воспользуемся формулой, приведенной в свойстве 5:

Видео:Запоминаем: высота, медиана биссектриса треугольникаСкачать

Медиана треугольника делит прямой угол в отношении 1:2

Что следует из того, что медиана делит прямой угол в отношении 1:2? Дано: ∆ ABC,

Какими свойствами обладают ∆ ABO и ∆ CBO?

1) Пусть k — коэффициент пропорциональности. Тогда ∠CBO=kº, ∠OBA=2kº.

Значит, ∠CBO=30º, ∠OBA=60º.

2) Поскольку медиана прямоугольного треугольника,проведенная из вершины прямого угла, равна половине гипотенузы, то

3) Из того, что BO=CO, следует, что треугольник CBO — равнобедренный с основанием BC (по определению равнобедренного треугольника).

Так как углы при основании равнобедренного треугольника равны, то ∠C=∠CBO=30º.

4) Аналогично, в треугольнике ABO

Так как сумма углов треугольника равна 180º, то ∠BOA=180º-(∠OAB+∠OBA)=60º.

Все углы треугольника ABO равны, значит, этот треугольник — равносторонний,

Если медиана делит прямой угол в отношении 1:2, то

— она разбивает исходный прямоугольный треугольник на два треугольника, один из которых — равносторонний, а другой — равнобедренный,

— боковые стороны равнобедренного треугольника равны сторонам равностороннего треугольника и равны меньшему катету,

— острые углы исходного прямоугольного треугольника равны 30º и 60º.

Проведем в треугольнике CBO высоту OF.

В прямоугольном треугольнике FCO ∠C=30º.

Видео:Свойство биссектрисы треугольника с доказательствомСкачать

Определение и свойства медианы треугольника

В данной статье мы рассмотрим определение медианы треугольника, перечислим ее свойства, а также разберем примеры решения задач для закрепления теоретического материала.

Видео:Медиана треугольника делит пополам угол ... | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

Определение медианы треугольника

Медиана – это отрезок, соединяющий вершину треугольника с серединой стороны, расположенной напротив данной вершины.

Основание медианы – точка пересечения медианы со стороной треугольника, другими словами, середина этой стороны (точка F).

Видео:Построение медианы в треугольникеСкачать

Свойства медианы

Свойство 1 (основное)

Т.к. в треугольнике три вершины и три стороны, то и медиан, соответственно, тоже три. Все они пересекаются в одной точке (O), которая называется центроидом или центром тяжести треугольника.

В точке пересечения медиан каждая из них делится в отношении 2:1, считая от вершины. Т.е.:

Свойство 2

Медиана делит треугольник на 2 равновеликих (равных по площади) треугольника.

Свойство 3

Три медианы делят треугольник на 6 равновеликих треугольников.

Свойство 4

Наименьшая медиана соответствует большей стороне треугольника, и наоборот.

• AC – самая длинная сторона, следовательно, медиана BF – самая короткая.
• AB – самая короткая сторона, следовательно, медиана CD – самая длинная.

Свойство 5

Допустим, известны все стороны треугольника (примем их за a, b и c).

Длину медианы m_a, проведенную к стороне a, можно найти по формуле:

Видео:8. Медиана треугольника и её свойства.Скачать

Примеры задач

Задание 1
Площадь одной из фигур, образованной в результате пересечения трех медиан в треугольнике, равняется 5 см 2 . Найдите площадь треугольника.

Решение
Согласно свойству 3, рассмотренному выше, в результате пересечения трех медиан образуются 6 треугольников, равных по площади. Следовательно:
S_△ = 5 см 2 ⋅ 6 = 30 см 2 .

Задание 2
Стороны треугольника равны 6, 8 и 10 см. Найдите медиану, проведенную к стороне с длиной 6 см.

Решение
Воспользуемся формулой, приведенной в свойстве 5:

💥 Видео

Геометрия 7 класс (Урок№12 - Медианы треугольника. Биссектрисы треугольника. Высоты треугольника.)Скачать

ГЕОМЕТРИЯ 7 класс. Медиана прямоугольного треугольника. Свойство. Доказательство для 7 класса.Скачать

Теорема о точке пересечения медиан треугольника. Доказательство. 8 класс.Скачать

Высота и медиана делят угол на три равных!Скачать

Медиана делит треугольник на два равновеликих. ДоказательствоСкачать

Формулы для медианы треугольникаСкачать

Медиана в прямоугольном треугольникеСкачать

Все факты о медиане треугольника для ЕГЭСкачать

Медиана в прямоугольном треугольникеСкачать