Как измерить треугольник линейкой (8 видео)

Digitrode

Содержание

цифровая электроника вычислительная техника встраиваемые системы
Как измерить угол с помощью линейки
Измерение углов
Объясняем ребенку на пальцах одной руки, сколько градусов в угле
Метки
Сколько градусов в угле
Измеряем угол без транспортира
Строим углы в 90, 60 и 30 градусов без транспортира
🌟 Видео

Видео:КАК ИЗМЕРИТЬ УГОЛ БЕЗ ТРАНСПОРТИРА С ПОМОЩЬЮ ЛИНЕЙКИ И КАЛЬКУЛЯТОРА | МАТЕМАТИКА ДЛЯ ВСЕХСкачать

цифровая электроника вычислительная техника встраиваемые системы

Как измерить угол с помощью линейки

Как бы хорошо вы ни старались подготовиться, иногда случаются непредвиденные обстоятельства, и у вас нет под рукой нужных инструментов для выполнения работы. Архитекторам, инженерам и плотникам часто приходится измерять углы, например, угол, образованный землей и деревянными перилами на лестничном марше. Транспортир – это обычный инструмент для работы. Однако, когда транспортир недоступен, достаточно обычной линейки и калькулятора.

Удерживайте одну из линий так, чтобы она была на уровне земли. Если эта линия – земля, тем проще. Эта линия будет называться базовой. Линия, идущая под углом от основания, будет называться гипотенузой. Измерьте длину прямой от вершины гипотенузы до основания. Эта линия будет называться ногой.

Измерьте длину гипотенузы и отрезка линейкой. Будьте максимально точными при измерениях, так как это гарантирует, что результат будет таким же точным, как измерение угла с помощью транспортира.

Разделите длину участка на длину гипотенузы с помощью калькулятора. Это дает вам синус угла, который вы хотите определить. Синус — это тригонометрическая функция. Он определяется по отношению к прямоугольному треугольнику, который представляет собой треугольник с углом в 90 градусов. Любой из других углов (углы менее 90 градусов) можно использовать для определения определенных функций, называемых «тригонометрическими функциями». Синус одного из этих углов равен длине стороны, противоположной этому углу (катету), деленной на самую длинную сторону треугольника, которая является гипотенузой.

Нажмите кнопку «обратный синус» (inverse sine). Обычно он обозначается аббревиатурой «sin» с отрицательной цифрой 1, написанной над ним и справа. Эта кнопка сообщит вам угол, при котором возник этот конкретный синус. Результатом этого расчета является угол, который вы хотели измерить.

Видео:Площадь треугольника. Как найти площадь треугольника?Скачать

Измерение углов

Андрей Андреев, Полина Ачева, Алексей Панов
«Квантик» №12, 2020

В школьной геометрии угол — это фигура, состоящая из двух лучей, выходящих из одной точки (рис. 1). Эта точка называется вершиной угла, а лучи — его сторонами. Угол разбивает плоскость на две части: на рисунке 2 они окрашены в зелёный и жёлтый цвет. Эти части называются плоскими углами.

Измерить угол можно обычным транспортиром, который размечен в градусах от 0° до 180° (рис. 3, слева).

Рис. 2 (слева). Два плоских угла — зелёный и жёлтый. Рис. 3. Транспортиры — полукруговой и круговой

Плоские углы удобно измерять круговым транспортиром, размеченным от 0° до 360° (рис. 3, справа). Конечно, для научных и технических измерений углов нужны более точные приборы: например, такие, как на рисунке 4. Слева там изображён один из астрономических инструментов Тихо Браге, с которым он проводил свои высокоточные наблюдения. Результаты этих наблюдений позволили Кеплеру вывести законы движения планет. Справа — современный электронный теодолит, используемый в геодезии.

Рис. 4. Секстант Тихо Браге и современный теодолит

А можно ли измерять углы, не применяя вообще никаких инструментов?

«Ручное измерение» углов. Об этом методе мы прочли в книге «Музыка сфер. Математика и астрономия», написанной Розой Марией Рос. Цитируем:

. Существует очень простой, хотя и не слишком точный, способ измерения углов вручную. Если мы вытянем руку перед собой, то растопыренная ладонь будет указывать интервал в 20°, кулак — 10°, большой палец — 2°, мизинец — 1°. Этот способ могут использовать и взрослые, и дети, так как размеры ладони человека увеличиваются пропорционально длине его руки.

Поясним сказанное. Пусть мы наблюдаем за двумя звёздами, расположенными на небе недалеко друг от друга. Направление взгляда на каждую из них задаёт луч. Угол между этими двумя лучами (с вершиной в глазу наблюдателя) мы и хотим измерить. Его величина называется угловым расстоянием между звёздами. Вытянем правую руку с растопыренной ладонью, как на рисунке 5 справа. Если кончик большого пальца закрывает одну звезду, а кончик мизинца — другую, угловое расстояние между звёздами можно оценить в 20°. Прикладывая ладони друг к другу, можно измерять углы до 40° (рис. 5, справа внизу).

Рис. 5. Ручное измерение углов

Задача 1. Звёздной ночью найдите на небе ковш Большой Медведицы (рис. 6) и «вручную» оцените угловое расстояние между звёздами Мерак и Дубхе.

Рис. 6. Ковш Большой Медведицы

Напомним: в направлении Мерак → Дубхе расположена Полярная звезда, указывающая путь на север.

Задача 2. Отыщите на небе Полярную звезду и найдите угловое расстояние между ней и звездой Дубхе.

Решив задачи, вы сможете проверить себя, так как известно, что расстояние Дубхе — Полярная звезда примерно в 5 раз больше расстояния Мерак — Дубхе.

Конечно, ручное измерение углов не позволяет добиться хорошей точности. Сейчас мы опишем бесприборный метод измерения углов, позволяющий проводить измерения со сколь угодно высокой точностью. Начнём с нескольких экспериментов.

Рис. 7. Треугольник

Эксперименты с треугольниками: «60°» ≠ 60°. Мы купили несколько одинаковых треугольников, как на рисунке 7. Углы этого треугольника по стандарту должны быть равны 30°, 60° и 90°, но мы хотим проверить, так ли это на самом деле. Начнём со среднего по величине из этих углов, обозначив его α. Итак, верно ли, что α = 60°?

Рис. 8. Каждый треугольник получается из соседнего поворотом на угол α, см. видео

Эксперимент № 1: поворачиваем треугольники. Выложим на плоскость один за другим шесть треугольников, как на рисунке 8: каждый получен из соседнего поворотом на угол α.

Видно, что первый и последний треугольники не сомкнулись, и это означает, что в сумме шесть одинаковых углов α дают меньше 360°, то есть 6α 360°, откуда α > 360°/7. Объединим полученные два неравенства и запишем их в виде

Эксперимент № 2: переворачиваем треугольники. На рисунке 9 представлен другой способ выкладывания треугольников. Каждый треугольник получается из соседнего переворотом вокруг их общей стороны на 180°. Этот способ даёт такую же оценку измеряемого угла, но он будет удобнее для нас в дальнейшем.

Практический совет: чтобы треугольники не смещались при малейшем прикосновении, не укладывайте их на скользкую поверхность. На видео мы воспользовались оборотной стороной коврика для ванной: она сделана из материала, не скользящего даже по влажному гладкому полу ванной комнаты, и идеально подходит для наших экспериментов.

Уменьшаем число треугольников, увеличиваем точность измерения. Первое усовершенствование: будем использовать единственный экземпляр треугольника. Опять обозначим один из его углов через α. Нарисуем на плоскости луч и совместим вершину угла с вершиной луча, а одну из сторон угла направим вдоль луча, как на рисунке 7. Перевернём треугольник вокруг другой стороны угла (не лежащей на луче). Потом перевернём треугольник вокруг другой стороны угла, опять перевернём и т. д., пока максимально не приблизимся к нарисованному лучу. Так мы определим максимальное k, для которого kα 360°, то есть

Задача 3. На рисунке 10 представлен угол α . Увеличьте рисунок и по этому шаблону из тонкого жёсткого листа пластика вырежьте соответствующий плоский угол. Используя разобранный нами метод измерения, с помощью переворотов оцените величину этого угла. Тут вас ждёт небольшой сюрприз. Угол на рисунке подобран специальным образом. Существует такое небольшое число n, что величина α укладывается в n · 360° целое число раз. Так что с помощью нашего метода вы сможете определить это n и найти точное значение угла α.

Задача 4 (Г. Фельдман, Д. Баранов, XXXI Турнир городов). Нарисован угол, и ещё имеется только циркуль.

Какое наименьшее число окружностей надо провести, чтобы наверняка определить, является ли данный угол острым?
Как определить, равен ли данный угол 31° (разрешается проводить сколько угодно окружностей)?

В пункте б можно обойтись и без циркуля, если есть деревянный угольник с данным углом, о котором мы хотим выяснить, равен ли он 31°.

И напоследок — небольшой список увлекательных книг, в которых обсуждается измерение углов в астрономии и геометрии, с небольшими аннотациями.

Роза Мария Рос. Музыка сфер. Астрономия и математика (М.: Де Агостини, 2014). В этой замечательной книге рассказывается о планетах и звёздах, об измерении углов, космических расстояний и времени.
Александр Шень. Космография (М.: МЦНМО, 2019). В книге разбираются основные вопросы космографии: как движутся звёзды по небу, отчего бывают зима и лето, почему Луна видна в форме серпа, когда и как происходят затмения. Прочитав её, вы поймёте, что астрономия не может обойтись без измерения углов.
Яков Перельман. Занимательная геометрия на вольном воздухе и дома, 7-е изд. (М.-Л.: ГИТТЛ, 1950). Обязательно обратите внимание на эту книгу. В третьей главе разобрано много задач на измерение углов подручными средствами и подробно рассказано о простейших устройствах для измерения углов, в том числе о посохе Якова и о грабельном угломере.
Особо рекомендуем раздел «Определение величины данного угла без всяких измерений» (с. 138–140), где описан метод измерения углов, «предложенный в 1946 г. З. Рупейка из Каунаса». По-видимому, этот раздел был добавлен редактором седьмого издания книги Б. А. Кордемским. Сам Яков Перельман скончался в 1942 году в блокадном Ленинграде.
Александр Шень. Геометрия в задачах (М.: МЦНМО, 2017). Второй раздел этой книги как раз называется «Измерение углов». Там много интересных задач, над которыми стоит подумать. Среди них мы выделим задачу № 38.

Видео:КАК ИЗМЕРИТЬ УГЛЫ ТРЕУГОЛЬНИКА ТРАНСПОРТИРОМ? Примеры | МАТЕМАТИКА 5 классСкачать

Объясняем ребенку на пальцах одной руки, сколько градусов в угле

Метки

Как хотя бы примерно определить, сколько градусов в угле, если под рукой нет ни транспортира, ни угольника? «Так Просто!» знает остроумный способ и просто не может не поделиться им с читателями.

Видео:Построение медианы в треугольникеСкачать

Сколько градусов в угле

Общепринятой единицей измерения плоских углов является градус. Почему математики древности выбрали именно такую единицу и почему в окружности 360 градусов, а не, скажем, 1000, точно неизвестно.

Одна из гипотез усматривает тут связь с тем, что в году приблизительно 360 дней. Другая гласит, что шумеры выбрали число 360, основываясь на своей шестидесятеричной системе счисления.

Так или иначе, а углы присутствуют не только на страницах учебников, но и повсеместно окружают нас в реальной жизни. Прямой угол легко найти в очертаниях зданий, изгибах мебели и каждом печатном листе.

Без угла в 45 градусов ни один столяр не смастерит простейшую рамку. Угол в 60 градусов требуется для построения равносторонних треугольников. Угол 30 градусов используется редко, но помогает получить угол в 120 градусов, необходимый для построения правильного шестиугольника.

Видео:Построение высоты в треугольникеСкачать

Измеряем угол без транспортира

При наличии транспортира всё просто. Размести его центр в вершине угла, а основание совмести с одной из сторон. Проследи за второй стороной угла. В том месте, где она пересечет дугу транспортира, и будет указана величина угла в градусах.

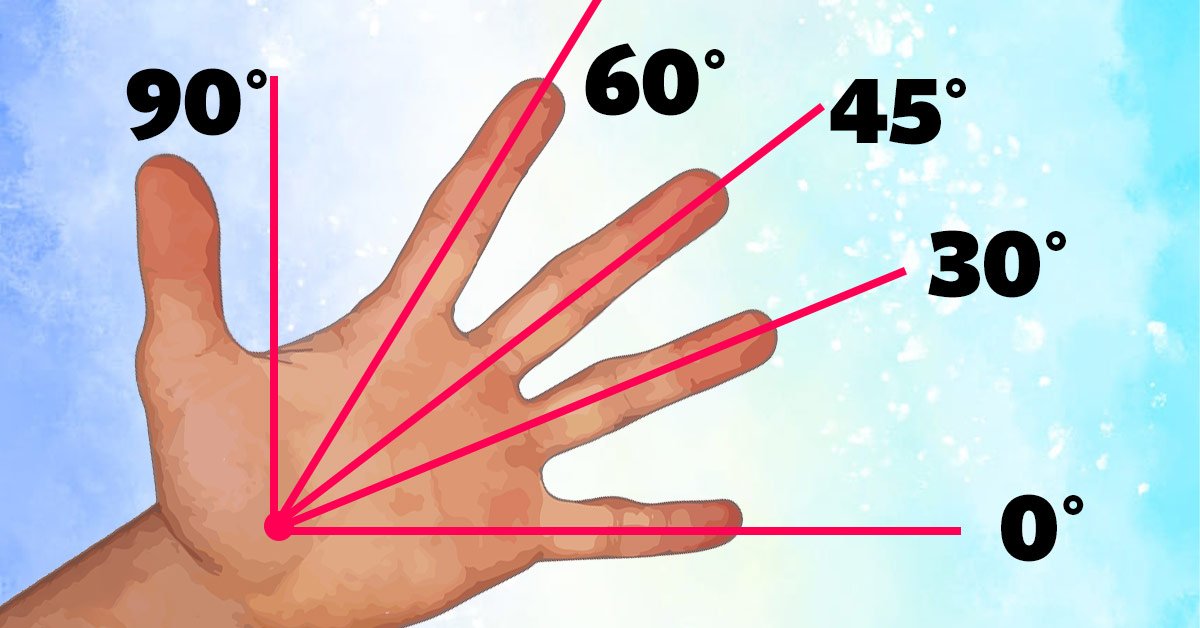
Без транспортира под рукой, как обычно и бывает, задача усложняется. Но смекалка выручит нас и здесь. Вытяни руку ладонью вверх и максимально расставь пальцы.

Следи за тем, чтобы большой палец находился перпендикулярно мизинцу. Тогда, если мизинец указывает на 0 градусов, то безымянный будет указывать на 30, средний на 45, указательный на 60, а большой на 90 градусов.

Способ, конечно, не очень точный, но всегда поможет приблизительно понять, с каким углом ты имеешь дело. Раньше мы рассказывали о полезном для каждого домашнего мастера угле в 22,5 градуса, который позволяет правильно заточить ножи. Выдержать его поможет сложенный вчетверо лист бумаги.

Видео:№102. Начертите треугольник. С помощью транспортира и линейки проведите его биссектрисы.Скачать

Строим углы в 90, 60 и 30 градусов без транспортира

Если нужен угол в 30, 60, 90 градусов, а транспортира или шаблона под рукой нет, помогут эти простые способы. Чтобы получить точный угол в 90 градусов, построй Пифагоров треугольник со сторонами, кратными 3,4,5.

Для этого, например, начерти отрезок длиной 5 см и проведи из его концов дуги с радиусами 3 и 4 см. Теперь соедини точку их пересечения с концами отрезка. Получится прямоугольный треугольник и угол, расположенный напротив гипотенузы, будет составлять ровно 90 градусов.

Когда уже есть прямой угол, легко получить углы в 30 и 60 градусов поможет магическое число 173 (его хорошо бы запомнить). Отложи по одной стороне прямого угла отрезок в 100 мм, а по другой — 173. Соедини их концы. Ты получишь шаблон с углами 90, 60 и 30 градусов!