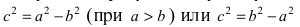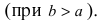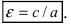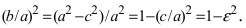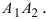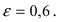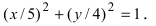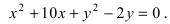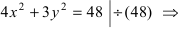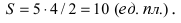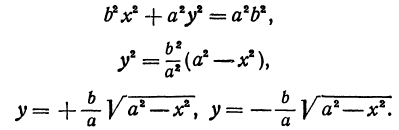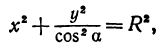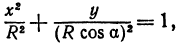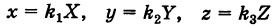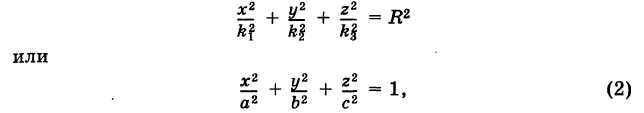- Понятие о кривых второго порядка
- Понятие алгебраической линии и её порядка
- Определение эллипсa
- Формула площади эллипса через каноническое уравнение
- Соотношения между элементами эллипса
- Элементы эллипсa
- Что такое канонический вид уравнения?
- Связанные определения
- Расчет площади
- Объяснение метода
- Эллипс, заданный каноническим уравнением
- Классификация линий второго порядка
- Что такое эллипс и фокусное расстояние
- Как построить эллипс?
- Свойства
- Формула длины окружности эллипса
- Эллипс — определение и вычисление с примерами решения
- Эллипс в высшей математике
- Уравнение эллипсоида
- Кривые второго порядка. Эллипс: формулы и задачи
- Понятие о кривых второго порядка
- Эллипс, заданный каноническим уравнением
- Решить задачи на эллипс самостоятельно, а затем посмотреть решение
- Продолжаем решать задачи на эллипс вместе
Видео:Длина эллипса и разложение в ряд для эллиптического интегралаСкачать

Понятие о кривых второго порядка
Кривыми второго порядка на плоскости называются линии, определяемые уравнениями, в которых переменные координаты x и y содержатся во второй степени. К ним относятся эллипс, гипербола и парабола.
Общий вид уравнения кривой второго порядка следующий:

где A, B, C, D, E, F – числа и хотя бы один из коэффициентов A, B, C не равен нулю.
При решении задач с кривыми второго порядка чаще всего рассматриваются канонические уравнения эллипса, гиперболы и параболы. К ним легко перейти от общих уравнений, этому будет посвящён пример 1 задач с эллипсами.
Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Понятие алгебраической линии и её порядка
Линию на плоскости называют алгебраической, если в аффинной системе координат её уравнение имеет вид 






Как видите, уравнение алгебраической линии не содержит синусов, косинусов, логарифмов и прочего функционального бомонда. Только «иксы» и «игреки» в целых неотрицательныхстепенях.
Далее под словом «линия» по умолчанию будет подразумеваться алгебраическая линия на плоскости
Порядок линии равен максимальному значению 
По соответствующей теореме, понятие алгебраической линии, а также её порядок не зависят от выбора аффинной системы координат , поэтому для лёгкости бытия считаем, что все последующие выкладки имеют место быть в декартовых координатах 
Общее уравнение линии второго порядка имеет вид 





Если 



Многие поняли смысл новых терминов, но, тем не менее, в целях 100%-го усвоения материала сунем пальцы в розетку. Чтобы определить порядок линии, нужно перебрать все слагаемыееё уравнения и у каждого из них найти сумму степенейвходящих переменных.
слагаемое 
слагаемое 
слагаемое 
в слагаемом 
Далее из полученных чисел выбирается максимальное значение, в данном случае единица, – это и есть порядок линии.
Теперь разберёмся, почему уравнение 
слагаемое 
у слагаемого 
у слагаемого 
слагаемое 
все остальные слагаемые – меньшей степени.
Максимальное значение: 2
Если к нашему уравнению дополнительно приплюсовать, скажем, 



В том случае, если добавить одно или несколько подходящих слагаемых, которые содержат 
С алгебраическими линиями 3-го, 4-го и более высоких порядков нам придется столкнуться ещё не раз, в частности, при знакомстве с полярной системой координат .
Однако вернёмся к общему уравнению 






Существенный недостаток общего уравнения состоит в том, что почти всегда не понятно, какую линию оно задаёт. Даже в простейшем случае 
Видео:Как начертить овал. Эллипс вписанный в ромбСкачать

Определение эллипсa
Эллипс — это замкнутая плоская кривая, сумма расстояний от каждой точки которой до двух точек F1 и F2 равна постоянной величине. Точки F1 и F2 называют фокусами эллипса.
 |  |
| Рис.1 | Рис.2 |
Видео:Как разметить эллипс, Как нарисовать эллипсСкачать

Формула площади эллипса через каноническое уравнение
Формула для нахождения площади в этом случае такова:
a , b – большая и мала полуоси эллипса, соответственно.
Решим задачу этим способом.
Дано уравнение эллипса. Найти его площадь и округлить ответ до целого числа.
2 5 x 2 + 9 y 2 = 1
Решение
Для начала найдем длины наших полуосей:
a = a 2 = 2 5 = 5
S = π ⋅ a ⋅ b = π ⋅ 5 ⋅ 3 ≈ 4 7 (см. кв.)
Ответ: 47 см. кв.
Видео:Аксонометрические Проекции Окружности #черчение #окружность #проекции #изометрияСкачать

Соотношения между элементами эллипса
- Малая полуось:
;
- Расстояние от фокуса до ближней вершины :
;
- Расстояние от фокуса до дальней вершины :
;
- Связь фокального параметра с полуосями и фокусным расстоянием:
;
;
;
;
- Связь фокального параметра с удалением вершин от данного фокуса:
;
;
Видео:ПОСТРОЕНИЕ ОВАЛА │ КАК НАЧЕРТИТЬ ОВАЛ ПРИ ПОСТРОЕНИИ АКСОНОМЕТРИИ │ Урок #61Скачать

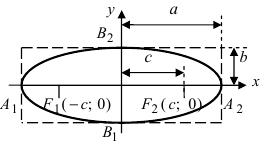
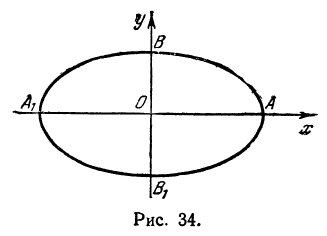
Элементы эллипсa
А1А2 = 2 a – большая ось эллипса (проходит через фокусы эллипса)
B1B2 = 2 b – малая ось эллипса (перпендикулярна большей оси эллипса и проходит через ее центр)
a – большая полуось эллипса
b – малая полуось эллипса
O – центр эллипса (точка пересечения большей и малой осей эллипса)
Эксцентриситет эллипсa e характеризует его растяженность и определяется отношением фокального расстояния c к большой полуоси a . Для эллипсa эксцентриситет всегда будет 0 e e = 0, для параболы e = 1, для гиперболы e > 1.
| e = | c |
| a |
Радиус эллипсa R – отрезок, соединяющий центр эллипсa О с точкой на эллипсе.
| R = | ab | = | b |
| √ a 2 sin 2 φ + b 2 cos 2 φ | √ 1 – e 2 cos 2 φ |
где e – эксцентриситет эллипсa, φ – угол между радиусом и большой осью A1A2.
| p = | b 2 |
| a |
Коэффициент сжатия эллипсa (эллиптичность) k – отношение длины малой полуоси к большой полуоси. Так как малая полуось эллипсa всегда меньше большей, то k k = 1:
| k = | b |
| a |
где e – эксцентриситет.
| 1 – k = | a – b |
| a |
Видео:ЭллипсСкачать

Что такое канонический вид уравнения?
Это общепринятый стандартный вид уравнения, когда в считанные секунды становится ясно, какой геометрический объект оно определяет. Кроме того, канонический вид очень удобен для решения многих практических заданий. Так, например, по каноническому уравнению 



Очевидно, что любая линия 1-го порядка представляет собой прямую. На втором же этаже нас ждёт уже не вахтёр, а гораздо более разнообразная компания из девяти статуй:
Видео:Изображение окружности в перспективе. Эллипс.Скачать

Связанные определения
- Отрезок AB, проходящий через фокусы эллипса, концы которого лежат на эллипсе, называется большой осью данного эллипса. Длина большой оси равна 2a в вышеприведённом уравнении.
- Отрезок CD, перпендикулярный большой оси эллипса, проходящий через центральную точку большой оси, концы которого лежат на эллипсе, называется малой осью эллипса.
- Точка пересечения большой и малой осей эллипса называется его центром.
- Точка пересечения эллипса с осями называются его вершинами.
- Отрезки, проведённые из центра эллипса к вершинам на большой и малой осях называются, соответственно, большой полуосью и малой полуосью эллипса, и обозначаются a и b.
- Расстояния r1 и r2 от каждого из фокусов до данной точки на эллипсе называются фокальными радиусами в этой точке.
- Расстояние
называется фокальным расстоянием.
- Эксцентриситетом эллипса называется отношение
. Эксцентриситет (также обозначается ε) характеризует вытянутость эллипса изменяется. Чем эксцентриситет ближе к нулю, тем эллипс больше напоминает окружность и наоборот, чем эксцентриситет ближе к единице, тем он более вытянут.
- Фокальным параметром
называется половина длины хорды , проходящей через фокус и перпендикулярной большой оси эллипса.
- Отношение длин малой и большой полуосей называется коэффициентом сжатия эллипса или эллиптичностью:
. Величина, равная
называется сжатием эллипса. Для окружности коэффициент сжатия равен единице, сжатие — нулю. Коэффициент и эксцентриситет эллипса связаны соотношением
Видео:Как начертить овал. Уроки черчения.Скачать

Расчет площади
- Большая полуось эллипса является максимальным расстоянием от его центра до края. [1]
- Малая полуось эллипса расположена под прямым углом 90º к его большой полуоси, однако для нахождения площади нет необходимости определять углы.
- Малая полуось эллипса является минимальным расстоянием от его центра до края.
- Например, если большая полуось эллипса равна 5 единицам, а малая 3 единицам длины, то получим площадь 5 x 3 x π, или около 47 квадратных единиц длины.
- Если у вас нет под рукой калькулятора или на калькуляторе нет символа π, используйте вместо этого числа значение “3,14”.
Видео:построение эллипсаСкачать

Объяснение метода
Видео:Как начертить эллипс. Уроки черчения.Скачать

Эллипс, заданный каноническим уравнением
Определение эллипса. Эллипсом называется множество всех точек плоскости, таких, для которых сумма расстояний до точек, называемых фокусами, есть величина постоянная и бОльшая, чем расстояние между фокусами.
Фокусы обозначены как 


Каноническое уравнение эллипса имеет вид:

где a и b (a > b) – длины полуосей, т. е. половины длин отрезков, отсекаемых эллипсом на осях координат.
Прямая, проходящая через фокусы эллипса, является его осью симметрии. Другой осью симметрии эллипса является прямая, проходящая через середину отрезка 


Ось абсцисс эллипс пересекает в точках (a, О) и (- a, О), а ось ординат – в точках (b, О) и (- b, О). Эти четыре точки называются вершинами эллипса. Отрезок между вершинами эллипса на оси абсцисс называется его большой осью, а на оси ординат – малой осью. Их отрезки от вершины до центра эллипса называются полуосями.
Если a = b , то уравнение эллипса принимает вид 
Пример 1. Проверить, является ли линия, заданная общим уравнением 
Решение. Производим преобразования общего уравнения. Применяем перенос свободного члена в правую часть, почленное деление уравнения на одно и то же число и сокращение дробей:
Ответ. Полученное в результате преобразований уравнение является каноническим уравнением эллипса. Следовательно, данная линия – эллипс.
Пример 2. Составить каноническое уравнение эллипса, если его полуоси соответственно равны 5 и 4.
Решение. Смотрим на формулу канонического уравения эллипса и подставляем: бОльшая полуось – это a = 5 , меньшая полуось – это b = 4 . Получаем каноническое уравнение эллипса:

Точки 



называются фокусами.
называется эксцентриситетом эллипса.
Отношение b/a характеризует “сплюснутость” эллипса. Чем меньше это отношение, тем сильнее эллипс вытянут вдоль большой оси. Однако степень вытянутости эллипса чаще принято выражать через эксцентриситет, формула которого приведена выше. Для разных эллипсов эксцентриситет меняется в пределах от 0 до 1, оставаясь всегда меньше единицы.
Пример 3. Составить каноническое уравнение эллипса, если расстояние между фокусами равно 8 и бОльшая ось равна 10.
Решение. Делаем несложные умозаключения:
– если бОльшая ось равна 10, то её половина, т. е. полуось a = 5 ,
– если расстояние между фокусами равно 8, то число c из координат фокусов равно 4.
Подставляем и вычисляем:
Результат – каноническое уравнение эллипса:

Пример 4. Составить каноническое уравнение эллипса, если его бОльшая ось равна 26 и эксцентриситет 
Решение. Как следует и из размера большей оси, и из уравнения эксцентриситета, бОльшая полуось эллипса a = 13 . Из уравнения эсцентриситета выражаем число c, нужное для вычисления длины меньшей полуоси:

Вычисляем квадрат длины меньшей полуоси:
Составляем каноническое уравнение эллипса:
Пример 5. Определить фокусы эллипса, заданного каноническим уравнением 
Решение. Следует найти число c, определяющее первые координаты фокусов эллипса:

Получаем фокусы эллипса:
Видео:Деление окружности на 3; 6; 12 равных частейСкачать

Классификация линий второго порядка
С помощью специального комплекса действий любое уравнение линии второго порядка приводится к одному из следующих видов:
( 


1) 
2) 
3) 
4) 
5) 
6) 
7) 


9) 
У ряда читателей может сложиться впечатление неполноты списка. Например, в пункте № 7 уравнение 











Таким образом, существует девять и только девять различных видов линий 2-го порядка, но на практике наиболее часто встречаются эллипс, гипербола и парабола .
Сначала рассмотрим эллипс. Как обычно, я акцентирую внимание на тех моментах, которые имеют большое значение для решения задач, и если вам необходим подробный вывод формул, доказательства теорем, пожалуйста, обратитесь, например, к учебнику Базылева/Атанасяна либо Александрова.
Видео:Эллипс - Инженерная графика.Скачать

Что такое эллипс и фокусное расстояние
Внимание!
Если вам нужна помощь с академической работой , то рекомендуем обратиться к профессионалам. Более 70 000 экспертов готовы помочь вам прямо сейчас.
Эллипс – это множество точек плоскости, сумма расстояний которых от двух заданных точек, что называются фокусами, есть постоянная величина и равна .
Обозначим фокусы эллипса и . Допустим, что расстояние = – фокусное расстояние.



Фокусное расстояние и полуоси связаны соотношением:
Если точка 

Видео:7. Эллипс (AutoCad)Скачать

Как построить эллипс?
Да, вот взять его и просто начертить. Задание встречается часто, и значительная часть студентов не совсем грамотно справляются с чертежом:
Построить эллипс, заданный уравнением
Решение: сначала приведём уравнение к каноническому виду:
Зачем приводить? Одно из преимуществ канонического уравнения 



В данном случае 

Отрезок 
отрезок 
отрезок 
число 
число 
число 
в нашем примере: 
Чтобы быстро представить, как выглядит тот или иной эллипс достаточно посмотреть на значения «а» и «бэ» его канонического уравнения.
Всё ладно, складно и красиво, но есть один нюанс: я выполнил чертёж с помощью программы . И вы можете выполнить чертёж с помощью какого-либо приложения. Однако в суровой действительности на столе лежит клетчатый листок бумаги, и на наших руках водят хороводы мыши. Люди с художественным талантом, конечно, могут поспорить, но мыши есть и у вас тоже (правда, поменьше). Таки не зря человечество изобрело линейку, циркуль, транспортир и другие нехитрые приспособления для черчения.
По этой причине нам вряд ли удастся аккуратно начертить эллипс, зная одни вершины. Ещё куда ни шло, если эллипс небольшой, например, с полуосями 
Существует два подхода к построению эллипса – геометрический и алгебраический. Построение с помощью циркуля и линейки мне не нравится по причине не самого короткого алгоритма и существенной загроможденности чертежа. В случае крайней необходимости, пожалуйста, обратитесь к учебнику, а в реальности же гораздо рациональнее воспользоваться средствами алгебры. Из уравнения эллипса 

Далее уравнение распадается на две функции:



Заданный каноническим уравнением эллипс симметричен относительно координатных осей, а также относительно начала координат. И это отлично – симметрия почти всегда предвестник халявы. Очевидно, что достаточно разобраться с 1-й координатной четвертью, поэтому нам потребуется функция 


Безусловно, приятно и то, что если допущена серьёзная ошибка в вычислениях, то это сразу выяснится в ходе построения.
Отметим на чертеже точки 

Первоначальный набросок лучше прочертить тонко-тонко, и только потом придать нажим карандашу. В результате должен получиться вполне достойный эллипс. Кстати, не желаете ли узнать, что это за кривая?
Видео:4K Построение эллипса по точкам, ellipse constructionСкачать

Свойства
- Фокальное свойство. Если F1 и F2 — фокусы эллипса, то для любой точки X, принадлежащей эллипсу, угол между касательной в этой точке и прямой (F1X) равен углу между этой касательной и прямой (F2X) .
- Прямая, проведённая через середины отрезков, отсечённых двумя параллельными прямыми, пересекающими эллипс, всегда будет проходить через центр эллипса. Это позволяет построением с помощью циркуля и линейки легко получить центр эллипса, а в дальнейшем оси, вершины и фокусы.
- Эволютой эллипса является астроида .
Эллипс также можно описать как
- фигуру, которую можно получить из окружности , применяя аффинное преобразование
- ортогональную проекцию окружности на плоскость .
- Пересечение плоскости и кругового цилиндра
Видео:КАК РИСОВАТЬ ЭЛЛИПСЫ. Простой и быстрый способ рисования ЭЛЛИПСОВСкачать

Формула длины окружности эллипса
Хотя рассматриваемая фигура является достаточно простой, длину ее окружности точно можно определить, если вычислить так называемые эллиптические интегралы второго рода. Однако, индусский математик-самоучка Рамануджан еще в начале XX века предложил достаточно простую формулу длины эллипса, которая приближается к результату отмеченных интегралов снизу. То есть рассчитанное по ней значение рассматриваемой величины будет немного меньше, чем реальная длина. Эта формула имеет вид: P ≈ pi * [3 * (a+b) – √((3 * a + b) * (a + 3 * b))], где pi = 3,14 – число пи.
Например, пусть длины двух полуосей эллипса будут равны a = 10 см и b = 8 см, тогда его длина P = 56,7 см.
Каждый может проверить, что если a = b = R, то есть рассматривается обычная окружность, тогда формула Рамануджана сводится к виду P = 2 * pi * R.
Отметим, что в школьных учебниках часто приводится другая формула: P = pi * (a + b). Она является более простой, но и менее точной. Так, если ее применить для рассмотренного случая, то получим значение P = 56,5 см.
Видео:Аналитическая геометрия: окружность и эллипсСкачать
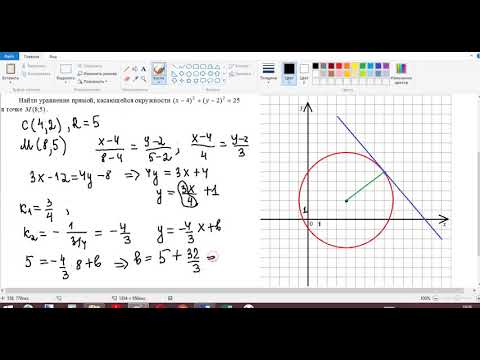
Эллипс — определение и вычисление с примерами решения
Эллипс:
Определение: Эллипсом называется геометрическое место точек, сумма расстояний от которых до двух выделенных точек
Получим каноническое уравнение эллипса. Выберем декартову систему координат так, чтобы фокусы
Рис. 29. Вывод уравнения эллипса.
Расстояние между фокусами (фокусное расстояние) равно 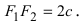
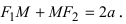
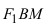
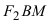
соответственно. Следовательно, согласно определению имеем
Возведем обе части равенства в квадрат, получим
Перенося квадратный корень в левую часть, а все остальное в правую часть равенства, находим 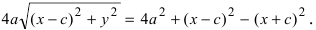
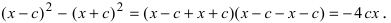
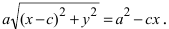
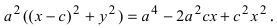
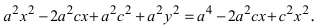
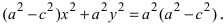
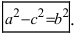
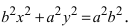
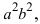
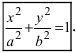
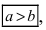
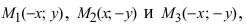
т.е. точками пересечения эллипса с осью абсцисс будут точки
т.е. точками пересечения эллипса с осью ординат будут точки
(Рис. 30).
Определение: Найденные точки называются вершинами эллипса.
Рис. 30. Вершины, фокусы и параметры эллипса
Определение: Если 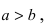
Определение: Эксцентриситетом эллипса называется отношение фокусного рас- стояния к большой полуоси эллипса
Из определения эксцентриситета эллипса следует, что он удовлетворяет двойному неравенству 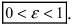
Если 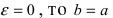
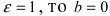
Пример:
Составить уравнение эллипса, если его большая полуось а = 5, а его эксцентриситет
Решение:
Исходя из понятия эксцентриситета, найдем абсциссу фокуса, т.е. параметр 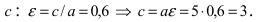
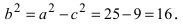
Пример:
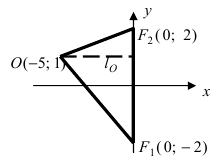
Найти площадь треугольника, две вершины которого находятся в фокусах эллипса 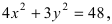
Решение:
Для определения координат фокусов эллипса и центра окружности преобразуем их уравнения к каноническому виду. Эллипс:
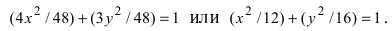
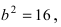
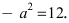
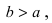
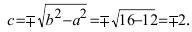
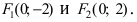
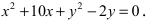
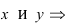
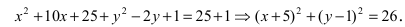
Построим в декартовой системе координат треугольник 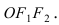
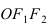
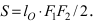
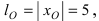
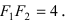
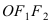
Видео:Как начертить эллипс (овал) на потолкеСкачать

Эллипс в высшей математике
где 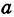
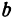
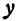
Отсюда видно, что уравнение (2) определяет две функции. Пока независимое переменное 
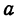

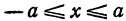
При 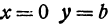
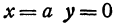
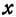

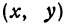
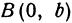
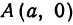
Полученная линия называется эллипсом. Число 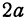
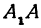
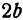
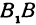
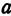
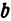
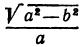
Пример:
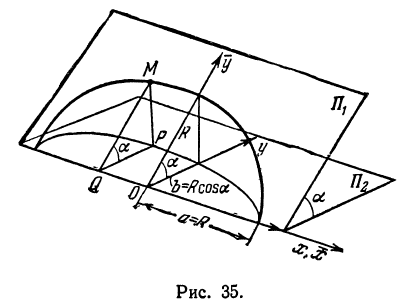
Найти проекцию окружности на плоскость, не совпадающую с плоскостью окружности.
Решение:
Возьмем две плоскости, пересекающиеся под углом 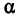
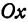
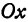
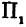
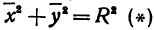
Пусть точка 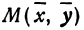
Обозначим проекцию точки 
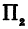
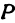
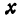
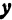


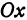
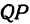
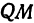
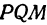
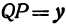
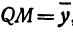
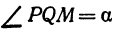
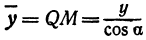


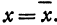
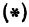
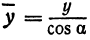
а это есть уравнение эллипса с полуосями 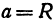
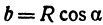
Таким образом, эллипс является проекцией окружности на плоскость, расположенную под углом к плоскости окружности.
Замечание. Окружность можно рассматривать как эллипс с равными полуосями.
Видео:Длина окружности. Математика 6 класс.Скачать

Уравнение эллипсоида
Определение: Трехосным эллипсоидом называется поверхность, полученная в результате равномерной деформации (растяжения или сжатия) сферы по трем взаимно перпендикулярным направлениям.
Рассмотрим сферу радиуса R с центром в начале координат:
где Х, У, Z — текущие координаты точки сферы.
Пусть данная сфера подвергнута равномерной деформации в направлении координатных осей 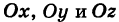
В результате сфера превратится в эллипсоид, а точка сферы М (X, У, Z) с текущими координатами Х, У, Z перейдет в точку эллипсоидам 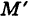
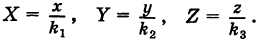
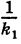
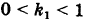
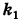
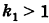
Подставляя эти формулы в уравнение (1), будем иметь
где 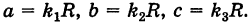
Величины 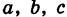
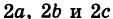
Если две полуоси эллипсоида равны между собой, то эллипсоид называется эллипсоидом вращения, так как может быть получен в результате вращения эллипса вокруг одной из его осей. Например, в геодезии считают поверхность земного шара эллипсоидом вращения с полуосями
а = b = 6377 км и с = 6356 км.
Если а = b = с, то эллипсоид превращается в сферу.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Гипербола
- Парабола
- Многогранник
- Решение задач на вычисление площадей
- Шар в геометрии
- Правильные многогранники в геометрии
- Многогранники
- Окружность
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Как начертить овал во фронтальной плоскостиСкачать

Кривые второго порядка. Эллипс: формулы и задачи
Понятие о кривых второго порядка
Кривыми второго порядка на плоскости называются линии, определяемые уравнениями, в которых переменные координаты x и y содержатся во второй степени. К ним относятся эллипс, гипербола и парабола.
Общий вид уравнения кривой второго порядка следующий:

где A, B, C, D, E, F — числа и хотя бы один из коэффициентов A, B, C не равен нулю.
При решении задач с кривыми второго порядка чаще всего рассматриваются канонические уравнения эллипса, гиперболы и параболы. К ним легко перейти от общих уравнений, этому будет посвящён пример 1 задач с эллипсами.
Эллипс, заданный каноническим уравнением
Определение эллипса. Эллипсом называется множество всех точек плоскости, таких, для которых сумма расстояний до точек, называемых фокусами, есть величина постоянная и бОльшая, чем расстояние между фокусами.
Фокусы обозначены как 

Каноническое уравнение эллипса имеет вид:

где a и b (a > b) — длины полуосей, т. е. половины длин отрезков, отсекаемых эллипсом на осях координат.
Прямая, проходящая через фокусы эллипса, является его осью симметрии. Другой осью симметрии эллипса является прямая, проходящая через середину отрезка 

Ось абсцисс эллипс пересекает в точках (a, О) и (- a, О), а ось ординат — в точках (b, О) и (- b, О). Эти четыре точки называются вершинами эллипса. Отрезок между вершинами эллипса на оси абсцисс называется его большой осью, а на оси ординат — малой осью. Их отрезки от вершины до центра эллипса называются полуосями.
Если a = b , то уравнение эллипса принимает вид 
Пример 1. Проверить, является ли линия, заданная общим уравнением 
Решение. Производим преобразования общего уравнения. Применяем перенос свободного члена в правую часть, почленное деление уравнения на одно и то же число и сокращение дробей:
Ответ. Полученное в результате преобразований уравнение является каноническим уравнением эллипса. Следовательно, данная линия — эллипс.
Пример 2. Составить каноническое уравнение эллипса, если его полуоси соответственно равны 5 и 4.
Решение. Смотрим на формулу канонического уравения эллипса и подставляем: бОльшая полуось — это a = 5 , меньшая полуось — это b = 4 . Получаем каноническое уравнение эллипса:

Точки 


называются фокусами.
называется эксцентриситетом эллипса.
Отношение b/a характеризует «сплюснутость» эллипса. Чем меньше это отношение, тем сильнее эллипс вытянут вдоль большой оси. Однако степень вытянутости эллипса чаще принято выражать через эксцентриситет, формула которого приведена выше. Для разных эллипсов эксцентриситет меняется в пределах от 0 до 1, оставаясь всегда меньше единицы.
Пример 3. Составить каноническое уравнение эллипса, если расстояние между фокусами равно 8 и бОльшая ось равна 10.
Решение. Делаем несложные умозаключения:
— если бОльшая ось равна 10, то её половина, т. е. полуось a = 5 ,
— если расстояние между фокусами равно 8, то число c из координат фокусов равно 4.
Подставляем и вычисляем:
Результат — каноническое уравнение эллипса:

Пример 4. Составить каноническое уравнение эллипса, если его бОльшая ось равна 26 и эксцентриситет 
Решение. Как следует и из размера большей оси, и из уравнения эксцентриситета, бОльшая полуось эллипса a = 13 . Из уравнения эсцентриситета выражаем число c, нужное для вычисления длины меньшей полуоси:

Вычисляем квадрат длины меньшей полуоси:
Составляем каноническое уравнение эллипса:
Пример 5. Определить фокусы эллипса, заданного каноническим уравнением 
Решение. Следует найти число c, определяющее первые координаты фокусов эллипса:

Получаем фокусы эллипса:
Решить задачи на эллипс самостоятельно, а затем посмотреть решение
Пример 6. Фокусы эллипса расположены на оси Ox симметрично относительно начала координат. Составить каноническое уравнение эллипса, если:
1) расстояние между фокусами 30, а большая ось 34
2) малая ось 24, а один из фокусов находится в точке (-5; 0)
3) эксцентриситет 
Продолжаем решать задачи на эллипс вместе
Если 



Для каждой точки, принадлежащей эллипсу, сумма расстояний от фокусов есть величина постоянная, равная 2a.
Прямые, определяемые уравнениями

называются директрисами эллипса (на чертеже — красные линии по краям).
Из двух вышеприведённых уравнений следует, что для любой точки эллипса

где 



Пример 7. Дан эллипс 
Решение. Смотрим в уравнение директрис и обнаруживаем, что требуется найти эксцентриситет эллипса, т. е. 

Получаем уравнение директрис эллипса:
Пример 8. Составить каноническое уравнение эллипса, если его фокусами являются точки 

Решение. Смотрим в уравнение директрис, видим, что в нём можем заменить символ эксцентриситета формулой эксцентриситета как отношение первой координаты фокуса к длине большей полуоси. Так сможем вычислить квадрат длины большей полуоси. Получаем:

Теперь можем получить и квадрат длины меньшей полуоси:
Уравнение эллипса готово:
Пример 9. Проверить, находится ли точка 

Решение. Подставляем координаты точки x и y в уравнение эллипса, на выходе должно либо получиться равенство левой части уравнения единице (точка находится на эллипсе), либо не получиться это равенство (точка не находится на эллипсе). Получаем:

Получили единицу, следовательно, точка находится на эллипсе.
Приступаем к нахождению расстояния. Для этого нужно вычислить: число c, определяющее первые координаты фокусов, число e — эксцентриситет и числа «эр» с подстрочными индексами 1 и 2 — искомые расстояния. Получаем:
Проведём проверку: сумма расстояний от любой точки на эллипсе до фокусов должна быть равна 2a.

так как из исходного уравнения эллипса 
Одним из самых замечательных свойств эллипса является его оптическое свойство, состоящее в том, что прямые, соединяющие точку эллипса с его фокусами, пересекают касательную к эллипсу под разными углами. Это значит, что луч, пущенный из одного фокуса, после отраэения попадёт в другой. Это свойство лежит в основе аккустического эффекта, наблюдаемого в некоторых пещерах и искусственных сооружениях, своды которых имеют эллиптическую форму: если находиться в одном из фокусов, то речь человека, стоящего в другом фокусе, слышна так хорошо, как будто он находится рядом, хотя на самом деле расстояние велико.

 ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; называется фокальным расстоянием.
называется фокальным расстоянием. . Эксцентриситет (также обозначается ε) характеризует вытянутость эллипса изменяется. Чем эксцентриситет ближе к нулю, тем эллипс больше напоминает окружность и наоборот, чем эксцентриситет ближе к единице, тем он более вытянут.
. Эксцентриситет (также обозначается ε) характеризует вытянутость эллипса изменяется. Чем эксцентриситет ближе к нулю, тем эллипс больше напоминает окружность и наоборот, чем эксцентриситет ближе к единице, тем он более вытянут. . Величина, равная
. Величина, равная  называется сжатием эллипса. Для окружности коэффициент сжатия равен единице, сжатие — нулю. Коэффициент и эксцентриситет эллипса связаны соотношением
называется сжатием эллипса. Для окружности коэффициент сжатия равен единице, сжатие — нулю. Коэффициент и эксцентриситет эллипса связаны соотношением 
















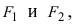
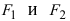
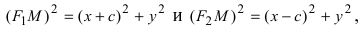
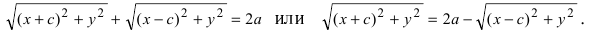
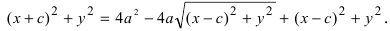
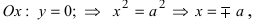 т.е. точками пересечения эллипса с осью абсцисс будут точки
т.е. точками пересечения эллипса с осью абсцисс будут точки 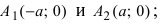
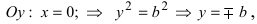 т.е. точками пересечения эллипса с осью ординат будут точки
т.е. точками пересечения эллипса с осью ординат будут точки 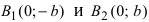 (Рис. 30).
(Рис. 30).