Выясним, какими свойствами обладают равные хорды и равные дуги.
Равные хорды равноудалены от центра окружности.


I. Рассмотрим треугольники AOB и COD.
1) AB=CD (по условию)
2) OA=OB=OC=OD (как радиусы).
Следовательно, ∆AOB = ∆COD (по трём сторонам).
Из равенства треугольников следует равенство соответствующих углов: ∠A=∠C.
II. Рассмотрим прямоугольные треугольники AOF и COK.
2) ∠A=∠C (по доказанному).
Из равенства треугольников следует равенство соответствующих сторон: OF=OK.
Что и требовалось доказать .
Если хорды равноудалены от центра окружности, то они равны.
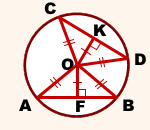
Соединим центр окружности с концами хорд.
I. Рассмотрим прямоугольные треугольники OKD и OFB.
1)OF=OK (по условию)
2)OD=OB (как радиусы).
Из равенства треугольников следует равенство соответствующих сторон:
II. Рассмотрим треугольники AOB и COD.
Так как OA=OB=OC=OD (как радиусы), треугольники AOB и COD — равнобедренные с основаниями AB и CD и высотами OK и OF соответственно.
По свойству равнобедренного треугольника, OK и OF — медианы, то есть AF=BF, CK=DK, откуда AB=CD.
Что и требовалось доказать.
Равные хорды стягивают равные дуги.
Дано : окр. (O;R), AB и CD — хорды, AB=CD,

Рассмотрим треугольники AOB и COD
1) AB=CD (по условию)
2) OA=OB=OC=OD (как радиусы).
Следовательно, ∆AOB = ∆COD (по трём сторонам).
Из равенства треугольников следует равенство соответствующих углов: ∠AOB=∠COD.
Значит и дуги, на которые опираются эти центральные углы, также равны: ∪AB=∪CD
Что и требовалось доказать .
Хорды, стягивающие равны дуги, равны.
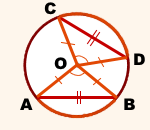
Соединим центр окружности с концами хорд.
Рассмотрим треугольники AOB и COD
Так как OA=OB=OC=OD (как радиусы), то треугольники AOB и COD — равнобедренные с основаниями AB и CD соответственно.
Так как ∪AB=∪CD (по условию), то ∠AOB=∠COD.
Из равенства треугольников следует равенство соответствующих сторон: AB=CD.
- Как доказать что хорды окружности параллельны то
- Отрезки и прямые, связанные с окружностью. Теорема о бабочке
- Отрезки и прямые, связанные с окружностью
- Свойства хорд и дуг окружности
- Теоремы о длинах хорд, касательных и секущих
- Доказательства теорем о длинах хорд, касательных и секущих
- Теорема о бабочке
- Хорда окружности — определение, свойства, теорема
- Хорда в геометрии
- Свойства отрезка окружности
- Ключевая теорема
- Касательная и секущая
- Решение задач
- Равные хорды
- Отрезки и прямые, связанные с окружностью. Теорема о бабочке
- Отрезки и прямые, связанные с окружностью
- Свойства хорд и дуг окружности
- Теоремы о длинах хорд, касательных и секущих
- Доказательства теорем о длинах хорд, касательных и секущих
- Теорема о бабочке
- 📽️ Видео
Видео:Геометрия 8 класс (Урок№28 - Свойства хорд окружности.)Скачать

Как доказать что хорды окружности параллельны то
Видео:Окружность, диаметр, хорда геометрия 7 классСкачать

Отрезки и прямые, связанные с окружностью. Теорема о бабочке
 Отрезки и прямые, связанные с окружностью Отрезки и прямые, связанные с окружностью |
 Свойства хорд и дуг окружности Свойства хорд и дуг окружности |
 Теоремы о длинах хорд, касательных и секущих Теоремы о длинах хорд, касательных и секущих |
 Доказательства теорем о длинах хорд, касательных и секущих Доказательства теорем о длинах хорд, касательных и секущих |
 Теорема о бабочке Теорема о бабочке |
Видео:№144. Отрезки АВ и CD — диаметры окружности. Докажите, что: а) хорды BD и АС равны; б) хорды AD и ВССкачать

Отрезки и прямые, связанные с окружностью
| Фигура | Рисунок | Определение и свойства |
| Окружность |  |
Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности

Конечная часть плоскости, ограниченная окружностью

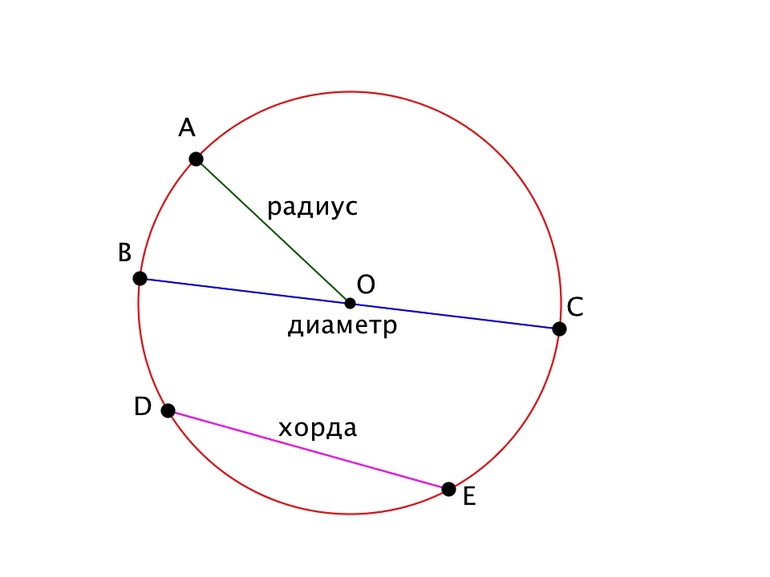
Отрезок, соединяющий центр окружности с любой точкой окружности

Отрезок, соединяющий две любые точки окружности

Хорда, проходящая через центр окружности.
Диаметр является самой длинной хордой окружности

Прямая, имеющая с окружностью только одну общую точку.
Касательная перпендикулярна к радиусу окружности, проведённому в точку касания

Прямая, пересекающая окружность в двух точках
| Окружность |
 |
Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности

Конечная часть плоскости, ограниченная окружностью

Отрезок, соединяющий центр окружности с любой точкой окружности

Отрезок, соединяющий две любые точки окружности

Хорда, проходящая через центр окружности.
Диаметр является самой длинной хордой окружности

Прямая, имеющая с окружностью только одну общую точку.
Касательная перпендикулярна к радиусу окружности, проведённому в точку касания

Прямая, пересекающая окружность в двух точках
Видео:ОГЭ Задание 26 Свойства хордСкачать

Свойства хорд и дуг окружности
| Фигура | Рисунок | Свойство |
| Диаметр, перпендикулярный к хорде |  | Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам. |
| Диаметр, проходящий через середину хорды | Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам. | |
| Равные хорды |  | Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности. |
| Хорды, равноудалённые от центра окружности | Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны. | |
| Две хорды разной длины |  | Большая из двух хорд расположена ближе к центру окружности. |
| Равные дуги |  | У равных дуг равны и хорды. |
| Параллельные хорды |  | Дуги, заключённые между параллельными хордами, равны. |
| Диаметр, перпендикулярный к хорде |
 |
Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам.

Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам.

Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности.

Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны.

Большая из двух хорд расположена ближе к центру окружности.

У равных дуг равны и хорды.

Дуги, заключённые между параллельными хордами, равны.
Видео:ОГЭ ЗАДАНИЕ 16 НАЙДИТЕ ДЛИНУ ХОРДЫ ОКРУЖНОСТИ ЕСЛИ РАДИУС 13 РАССТОЯНИЕ ДО ХОРДЫ 5Скачать

Теоремы о длинах хорд, касательных и секущих
| Фигура | Рисунок | Теорема |
| Пересекающиеся хорды |  |
Произведения длин отрезков, на которые разбита каждая из хорд, равны:

Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.


| Пересекающиеся хорды | ||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||
| Касательные, проведённые к окружности из одной точки | ||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||
| Касательная и секущая, проведённые к окружности из одной точки | ||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||
| Секущие, проведённые из одной точки вне круга | ||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||
| Пересекающиеся хорды |
 |
Произведения длин отрезков, на которые разбита каждая из хорд, равны:
Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Доказательства теорем о длинах хорд, касательных и секущих
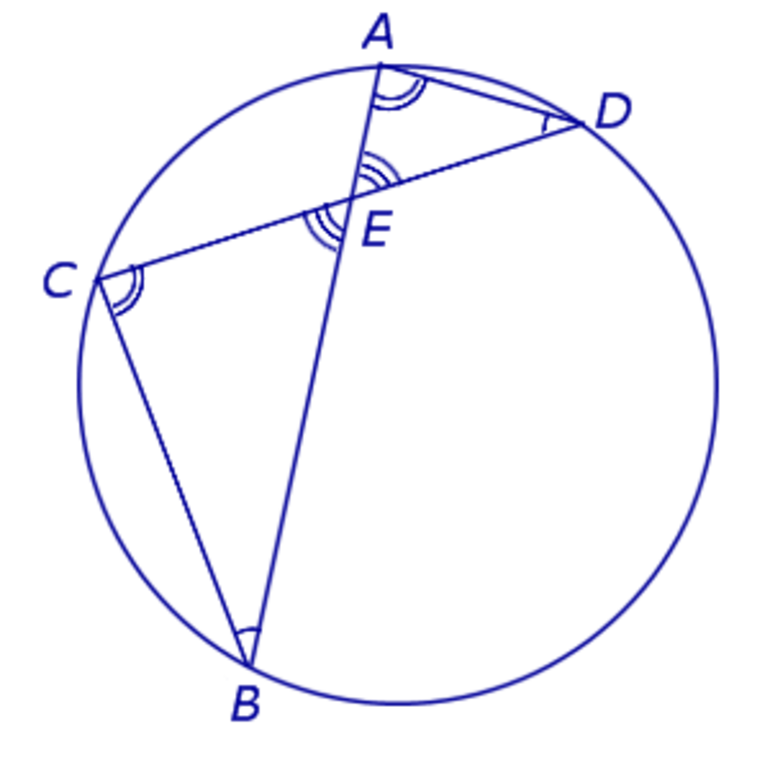
Теорема 1 . Предположим, что хорды окружности AB и CD пересекаются в точке E (рис.1).
Тогда справедливо равенство
Доказательство . Заметим, что углы BCD и BAD равны как вписанные углы, опирающиеся на одну и ту же дугу. Углы BEC и AED равны как вертикальные. Поэтому треугольники BEC и AED подобны. Следовательно, справедливо равенство
откуда и вытекает требуемое утверждение.
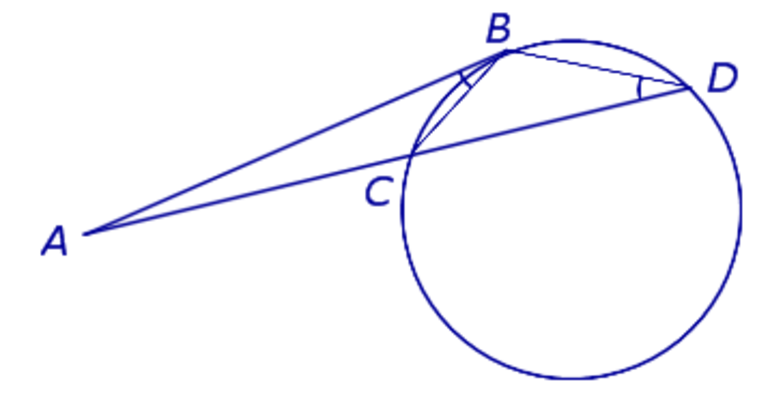
Теорема 2 . Предположим, что из точки A , лежащей вне круга, к окружности проведены касательная AB и секущая AD (рис.2).
Точка B – точка касания с окружностью, точка C – вторая точка пересечения прямой AD с окружностью. Тогда справедливо равенство
Доказательство . Заметим, что угол ABC образован касательной AB и хордой BC , проходящей через точку касания B . Поэтому величина угла ABC равна половине угловой величины дуги BC . Поскольку угол BDC является вписанным углом, то величина угла BDC также равна половине угловой величины дуги BC . Следовательно, треугольники ABC и ABD подобны (угол A является общим, углы ABC и BDA равны). Поэтому справедливо равенство
откуда и вытекает требуемое утверждение.
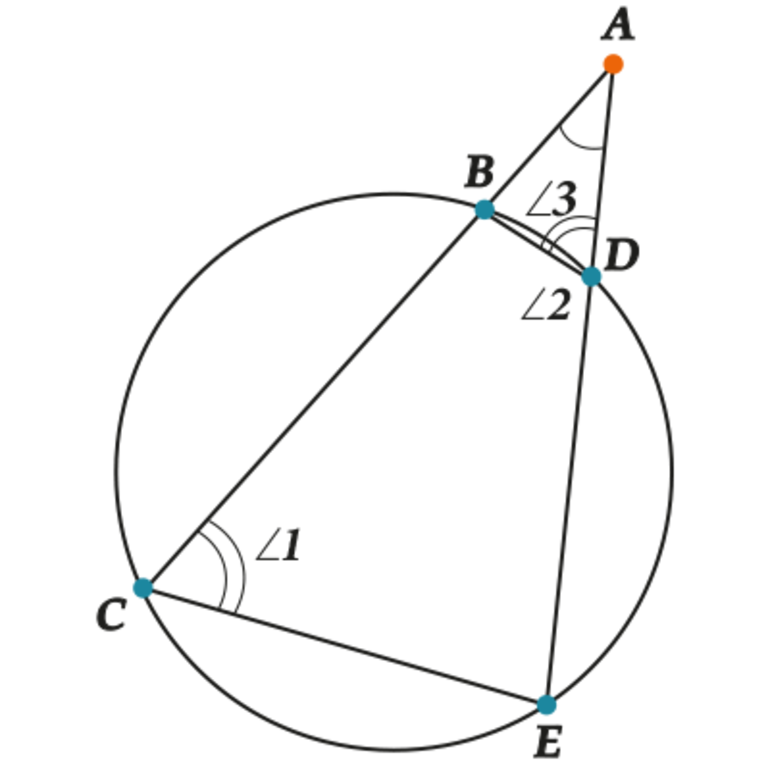
Теорема 3 . Предположим, что из точки A , лежащей вне круга, к окружности проведены секущие AD и AF (рис.3).
Точки C и E – вторые точки пересечения секущих с окружностью. Тогда справедливо равенство
Доказательство . Проведём из точки A касательную AB к окружности (рис. 4).
Точка B – точка касания. В силу теоремы 2 справедливы равенства
откуда и вытекает требуемое утверждение.
Видео:Длина хорды окружности равна 72 ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Теорема о бабочке
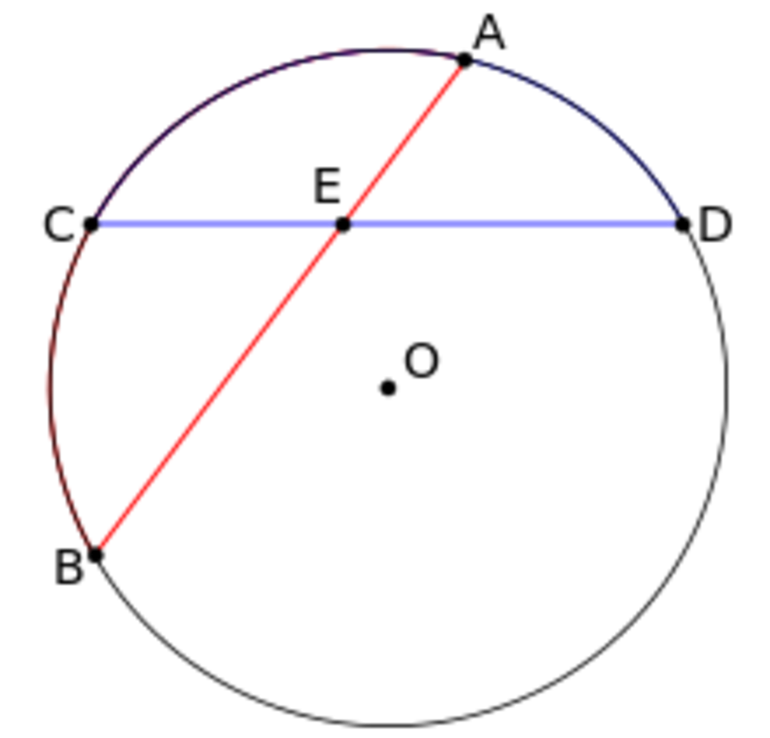
Теорема о бабочке . Через середину G хорды EF некоторой окружности проведены две произвольные хорды AB и CD этой окружности. Точки K и L – точки пересечения хорд AC и BD с хордой EF соответственно (рис.5). Тогда отрезки GK и GL равны.
Доказательство . Существует много доказательств этой теоремы. Изложим доказательство, основанное на теореме синусов, которое, на наш взгляд, является наиболее наглядным. Для этого заметим сначала, что вписанные углы A и D равны, поскольку опираются на одну и ту же дугу. По той же причине равны и вписанные углы C и B . Теперь введём следующие обозначения:
Воспользовавшись теоремой синусов, применённой к треугольнику CKG , получим
Воспользовавшись теоремой синусов, применённой к треугольнику AKG , получим
Воспользовавшись теоремой 1, получим
Воспользовавшись равенствами (1) и (2), получим
Проводя совершенно аналогичные рассуждения для треугольников BGL и DGL , получим равенство
откуда вытекает равенство
что и завершает доказательство теоремы о бабочке.
Видео:8 класс. Хорды в окружности (теория)Скачать

Хорда окружности — определение, свойства, теорема
Видео:ОГЭ Задание 25 Окружность Касательная ХордаСкачать
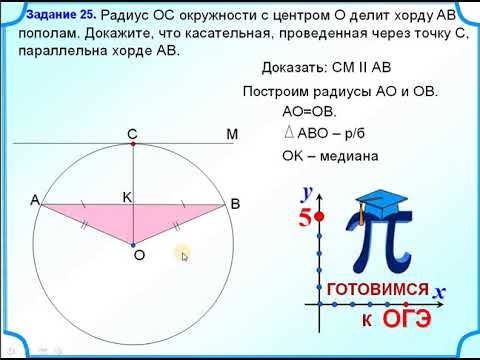
Хорда в геометрии
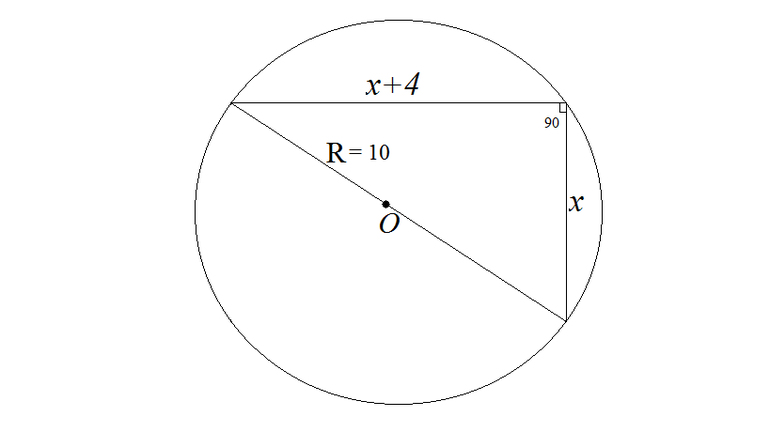
Каждая хорда имеет свою длину. Ее можно определить с помощью теоремы синусов. То есть длина хорды окружности зависит от радиуса и вписанного угла, опирающегося на данный отрезок. Формула для определения длины выглядит следующим образом: B*A = R*2 * sin α, где R — радиус, AB — это хорда, α — вписанный угол. Также длину можно вычислить через другую формулу, которая выводится из теоремы Пифагора: B*A = R*2 * sin α/2 , где AB — это хорда, α — центральный угол, который опирается на данный отрезок, R — радиус.
Если рассматривать хорды в совокупности с дугами, то получаются новые объекты. Например, в кругу можно дополнительно выделить две области: сектор и сегмент. Сектор образуется с помощью двух радиусов и дуги. Для сектора можно вычислить площадь, а если он является частью конуса, то еще и высоту. Сегмент, в свою очередь, это область, состоящая из отрезка и дуги.
Для того чтобы проверить правильность своего решения в нахождении длины, можно обратиться к онлайн-калькуляторам в интернете. Они представлены в виде таблицы, в которую нужно вписать только известные параметры, а программа сама выполнит необходимые вычисления.
Это очень полезная функция, так как не приходится вспоминать различные уравнения и производить сложные расчеты.
Свойства отрезка окружности
Для решения геометрических задач необходимо знать свойства хорды окружности. Для нее характерны такие показатели:
- Это отрезок с наибольшей длиною в окружности это диаметр. Он обязательно будет проходить через центр круга.
- Если есть две равные дуги, то их отрезки, которые их стягивают, будут равны.
- Хорда, которая перпендикулярна диаметру, будет делить этот отрезок и его дугу на две одинаковые части (справедливо и обратное утверждение).
- Самый маленький отрезок в окружности это точка.
- Хорды будут равны, если они находятся на одном расстоянии от центра окружности (справедливо и обратное утверждение).
- При сравнении двух отрезков в кругу большая из них окажется ближе к центру окружности.
- Дуги, которые находятся между двумя параллельными хордами, равны.
Помимо основных свойств отрезка круга, нужно выделить еще одно важное свойство. Оно отражено в теореме о пересекающихся хордах.
Ключевая теорема
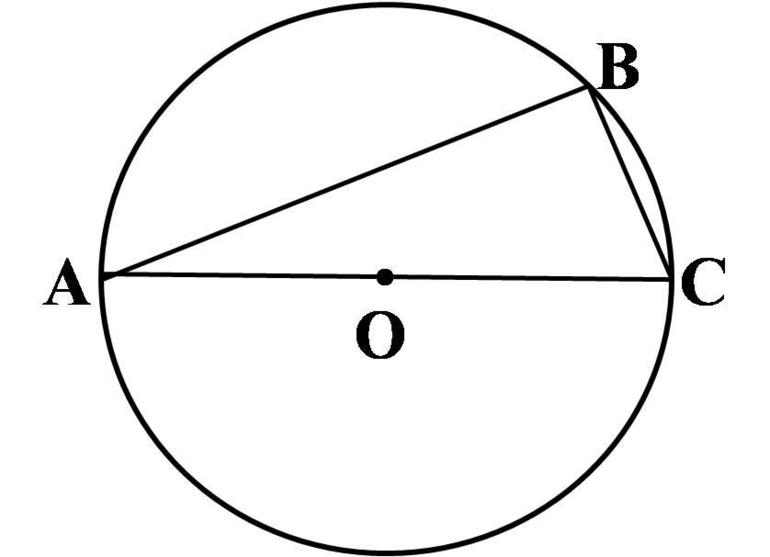
Имеется круг с центром в точке O и радиусом R. Для теоремы нужно в круг вписать две прямые, пускай это будут хорды BA и CD, которые пересекаются в точке E. Перед тем как перейти к доказательству, нужно сформулировать определение теоремы. Оно звучит следующим образом: если хорды пересекаются в некоторой точке, которая делит их на отрезки, то произведения длин отрезков первой хорды равно произведению длин отрезков второй хорды. Для наглядности можно записать эту формулу: AE*BE= EC*ED. Теперь можно перейти к доказательству.
Проведем отрезки CB и AD. Рассмотрим треугольники CEB и DEA. Известно, что углы CEB и DEA равны как вертикальные углы, DCB и BAD равны за следствием с теоремы про вписанные углы, которые опираются на одну и ту же дугу. Треугольники CEB и DEA подобны (первый признак подобия треугольников). Тогда выходит пропорциональное соотношение BE/ED = EC/EA. Отсюда AE*BE= EC*ED.
Помимо взаимодействия с внутренними элементами окружности, для хорды еще существуют свойства при пересечении с секущейся и касательными прямыми. Для этого необходимо рассмотреть понятия касательная и секущая и определить главные закономерности.
Касательная — это прямая, которая соприкасается с кругом только в одной точке. И если к ней провести радиус круга, то они будут перпендикулярны. В свою очередь, секущая — это прямая, которая проходит через две точки круга. При взаимодействии этих прямых можно заметить некоторые закономерности.
Видео:✓ Степень точки в ЕГЭ | Резерв досрока ЕГЭ-2022. Задание 16. Профильный уровень | Борис ТрушинСкачать

Касательная и секущая
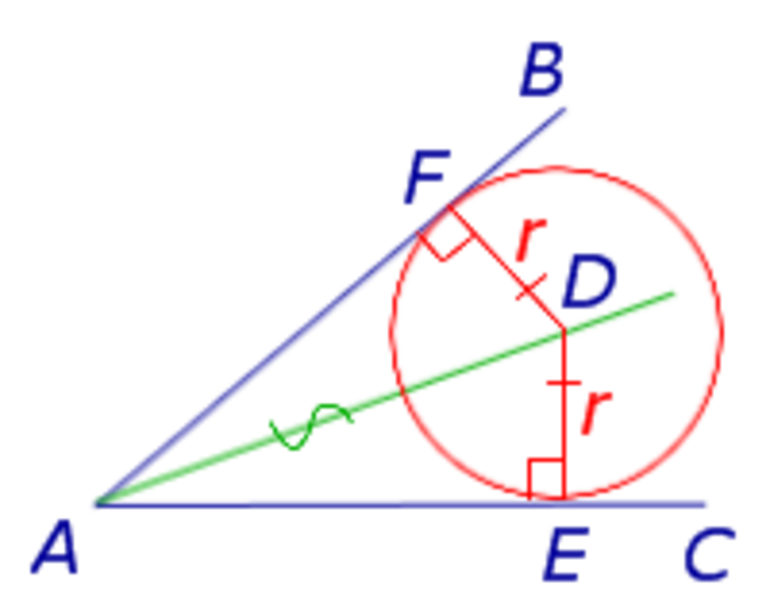
Существует теорема о двух касательных, которые проведены с одной точки. В ней говорится о том, что если есть две прямые OK и ON, которые проведены с точки O, будут равны между собой. Перейдем к доказательству теоремы.
Рассмотрим два прямоугольных треугольника AFD и AED. Поскольку катеты DF и DE будут равны как радиусы круга, а AD — общая гипотенуза, то между собой данные треугольники будут равны за признаком равенства треугольников, с чего выходит, что AF = AE.
Если возникает ситуация, когда пересекаются касательная и секущая, то в этом случае также можно вывести закономерность. Рассмотрим теорему и докажем, что AB 2 = AD*AC.
Предположим у нас есть касательная AB и секущая AD, которые берут начало с одной точки A. Обратим внимание на угол ABC, он спирается на дугу BC, значит, за свойством значение его угла будет равно половине градусной меры дуги, на которую он опирается. За свойством вписанного угла, величина угла BDC также будет равно половине дуги BC. Таким образом, треугольники ABD и ABC будут подобны за признаком подобия треугольников, так как угол A — общий, а угол ABC равен углу BDC. Опираясь на теорию, получаем соотношение: AB/CA = DA/AB, переписав это соотношение в правильную форму, получаем равенство AB 2 = AD*AC, что и требовалось доказать.
Как есть теорема про две касательные, так есть и теорема про две секущие. Она так же просто формулируется, как и остальные теоремы. Поэтому рассмотрим доказательство и убедимся, что AB*AC = AE*AD.
Проведем две прямые через точку A, получим две секущие AC и AE. Дорисуем две хорды, соединяя точки C и B, B и D. Получим два треугольника ABD И CEA. Обратим внимание на вписанный четырехугольник BDCE. За свойством вписанных четырехугольников узнаем, что значения углов BDE и ECB в сумме будут давать 180 градусов. И сумма значений углов BDA и BDE также равна 180, за свойством смежных углов.
Отсюда можно получить два уравнения, из которых будет выведено, что углы ECB и BDA будут равны: BDA + BDE = 180; BDE + ECB = 180. Все это записываем в систему уравнений, отнимаем первое от второго, получаем результат, что ECB = BDA.
Если вернутся к треугольникам ABD И CEA, то теперь можно сказать, что они подобны, так как угол А — общий, а углы ECA и BDA — равны. Теперь можно записать соотношение сторон: AB/AE = AD/AC. В итоге получим, что AB*AC = AE*AD.
Видео:Равные хорды, равные дугиСкачать

Решение задач
При решении задач, связанных с окружностью, хорда часто выступает главным элементом, опираясь на который можно найти остальные неизвестные элементы. В каждой второй задаче задаются два параметра, чтобы найти третий неизвестный. В задачах, которые, связанные с кругом, хорда — это обязательный элемент:
- Найти высоту детали, которая была получена путем сгибания заготовки в дугу. В начальных данных обязательно присутствует хорда и длина дуги.
- Дана развертка, нужно найти длину части кольца. Задается хорда и диаметр.
- Также можно находить длину хорды. В случае если заданы уравнения прямой и окружности, которые пересекаются.
Для решения задач с отрезком в окружности удобно использовать схематические рисунки. Их рисуют с помощью линейки и циркуля, и принцип решения задач становится более наглядным.
Видео:ЕГЭ-2022 ||Задание №6 || Найти длину хордыСкачать

Равные хорды
Выясним, какими свойствами обладают равные хорды и равные дуги.
Равные хорды равноудалены от центра окружности.


I. Рассмотрим треугольники AOB и COD.
1) AB=CD (по условию)
2) OA=OB=OC=OD (как радиусы).
Следовательно, ∆AOB = ∆COD (по трём сторонам).
Из равенства треугольников следует равенство соответствующих углов: ∠A=∠C.
II. Рассмотрим прямоугольные треугольники AOF и COK.
2) ∠A=∠C (по доказанному).
Из равенства треугольников следует равенство соответствующих сторон: OF=OK.
Что и требовалось доказать .
Если хорды равноудалены от центра окружности, то они равны.

Соединим центр окружности с концами хорд.
I. Рассмотрим прямоугольные треугольники OKD и OFB.
1)OF=OK (по условию)
2)OD=OB (как радиусы).
Из равенства треугольников следует равенство соответствующих сторон:
II. Рассмотрим треугольники AOB и COD.
Так как OA=OB=OC=OD (как радиусы), треугольники AOB и COD — равнобедренные с основаниями AB и CD и высотами OK и OF соответственно.
По свойству равнобедренного треугольника, OK и OF — медианы, то есть AF=BF, CK=DK, откуда AB=CD.
Что и требовалось доказать.
Равные хорды стягивают равные дуги.
Дано : окр. (O;R), AB и CD — хорды, AB=CD,

Рассмотрим треугольники AOB и COD
1) AB=CD (по условию)
2) OA=OB=OC=OD (как радиусы).
Следовательно, ∆AOB = ∆COD (по трём сторонам).
Из равенства треугольников следует равенство соответствующих углов: ∠AOB=∠COD.
Значит и дуги, на которые опираются эти центральные углы, также равны: ∪AB=∪CD
Что и требовалось доказать .
Хорды, стягивающие равны дуги, равны.

Соединим центр окружности с концами хорд.
Рассмотрим треугольники AOB и COD
Так как OA=OB=OC=OD (как радиусы), то треугольники AOB и COD — равнобедренные с основаниями AB и CD соответственно.
Так как ∪AB=∪CD (по условию), то ∠AOB=∠COD.
Из равенства треугольников следует равенство соответствующих сторон: AB=CD.
Видео:№145. Отрезок МК — диаметр окружности с центром О, а МР и РК — равные хорды этой окружностиСкачать

Отрезки и прямые, связанные с окружностью. Теорема о бабочке
 Отрезки и прямые, связанные с окружностью Отрезки и прямые, связанные с окружностью |
 Свойства хорд и дуг окружности Свойства хорд и дуг окружности |
 Теоремы о длинах хорд, касательных и секущих Теоремы о длинах хорд, касательных и секущих |
 Доказательства теорем о длинах хорд, касательных и секущих Доказательства теорем о длинах хорд, касательных и секущих |
 Теорема о бабочке Теорема о бабочке |
Видео:ищем хорду в окружности. огэ 1 часть геометрияСкачать

Отрезки и прямые, связанные с окружностью
| Фигура | Рисунок | Определение и свойства | ||||||||||||||||||||||||||
| Окружность |  | |||||||||||||||||||||||||||
| Круг |  | |||||||||||||||||||||||||||
| Радиус |  | |||||||||||||||||||||||||||
| Хорда |  | |||||||||||||||||||||||||||
| Диаметр |  | |||||||||||||||||||||||||||
| Касательная |  | |||||||||||||||||||||||||||
| Секущая |  | |||||||||||||||||||||||||||
| Окружность |
 |
Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности

Конечная часть плоскости, ограниченная окружностью

Отрезок, соединяющий центр окружности с любой точкой окружности

Отрезок, соединяющий две любые точки окружности

Хорда, проходящая через центр окружности.
Диаметр является самой длинной хордой окружности

Прямая, имеющая с окружностью только одну общую точку.
Касательная перпендикулярна к радиусу окружности, проведённому в точку касания

Прямая, пересекающая окружность в двух точках
Видео:Как найти диаметр окружности, зная длину хорды и расстояние от центра окружности до неё? #огэ #егэСкачать

Свойства хорд и дуг окружности
| Фигура | Рисунок | Свойство |
| Диаметр, перпендикулярный к хорде |  | Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам. |
| Диаметр, проходящий через середину хорды | Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам. | |
| Равные хорды |  | Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности. |
| Хорды, равноудалённые от центра окружности | Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны. | |
| Две хорды разной длины |  | Большая из двух хорд расположена ближе к центру окружности. |
| Равные дуги |  | У равных дуг равны и хорды. |
| Параллельные хорды |  | Дуги, заключённые между параллельными хордами, равны. |
| Диаметр, перпендикулярный к хорде |
 |
Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам.

Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам.

Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности.

Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны.

Большая из двух хорд расположена ближе к центру окружности.

У равных дуг равны и хорды.

Дуги, заключённые между параллельными хордами, равны.
Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Теоремы о длинах хорд, касательных и секущих
| Фигура | Рисунок | Теорема | ||||||||||||||||
| Пересекающиеся хорды |  | |||||||||||||||||
| Касательные, проведённые к окружности из одной точки |  | |||||||||||||||||
| Касательная и секущая, проведённые к окружности из одной точки |  | |||||||||||||||||
| Секущие, проведённые из одной точки вне круга |  | |||||||||||||||||
| Пересекающиеся хорды | ||
 | ||
| Касательные, проведённые к окружности из одной точки | ||
 | ||
| Касательная и секущая, проведённые к окружности из одной точки | ||
 | ||
| Секущие, проведённые из одной точки вне круга | ||
 | ||
| Пересекающиеся хорды |
 |
Произведения длин отрезков, на которые разбита каждая из хорд, равны:
Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.
Видео:Секретная теорема из учебника геометрииСкачать

Доказательства теорем о длинах хорд, касательных и секущих
Теорема 1 . Предположим, что хорды окружности AB и CD пересекаются в точке E (рис.1).
Тогда справедливо равенство
Доказательство . Заметим, что углы BCD и BAD равны как вписанные углы, опирающиеся на одну и ту же дугу. Углы BEC и AED равны как вертикальные. Поэтому треугольники BEC и AED подобны. Следовательно, справедливо равенство
откуда и вытекает требуемое утверждение.
Теорема 2 . Предположим, что из точки A , лежащей вне круга, к окружности проведены касательная AB и секущая AD (рис.2).
Точка B – точка касания с окружностью, точка C – вторая точка пересечения прямой AD с окружностью. Тогда справедливо равенство
Доказательство . Заметим, что угол ABC образован касательной AB и хордой BC , проходящей через точку касания B . Поэтому величина угла ABC равна половине угловой величины дуги BC . Поскольку угол BDC является вписанным углом, то величина угла BDC также равна половине угловой величины дуги BC . Следовательно, треугольники ABC и ABD подобны (угол A является общим, углы ABC и BDA равны). Поэтому справедливо равенство
откуда и вытекает требуемое утверждение.
Теорема 3 . Предположим, что из точки A , лежащей вне круга, к окружности проведены секущие AD и AF (рис.3).
Точки C и E – вторые точки пересечения секущих с окружностью. Тогда справедливо равенство
Доказательство . Проведём из точки A касательную AB к окружности (рис. 4).
Точка B – точка касания. В силу теоремы 2 справедливы равенства
откуда и вытекает требуемое утверждение.
Видео:Окружность. Длина хорды. Теорема синусов.Скачать

Теорема о бабочке
Теорема о бабочке . Через середину G хорды EF некоторой окружности проведены две произвольные хорды AB и CD этой окружности. Точки K и L – точки пересечения хорд AC и BD с хордой EF соответственно (рис.5). Тогда отрезки GK и GL равны.
Доказательство . Существует много доказательств этой теоремы. Изложим доказательство, основанное на теореме синусов, которое, на наш взгляд, является наиболее наглядным. Для этого заметим сначала, что вписанные углы A и D равны, поскольку опираются на одну и ту же дугу. По той же причине равны и вписанные углы C и B . Теперь введём следующие обозначения:
Воспользовавшись теоремой синусов, применённой к треугольнику CKG , получим
Воспользовавшись теоремой синусов, применённой к треугольнику AKG , получим
Воспользовавшись теоремой 1, получим
Воспользовавшись равенствами (1) и (2), получим
Проводя совершенно аналогичные рассуждения для треугольников BGL и DGL , получим равенство
откуда вытекает равенство
что и завершает доказательство теоремы о бабочке.
📽️ Видео
Решение задачи 25 из ОГЭ по математике 9 классСкачать

✓ Всё, что нужно знать про окружность | ЕГЭ. Задания 1 и 16. Профильный уровень | Борис ТрушинСкачать