Как чертить равносторонний прямоугольный треугольник (2 видео)

Как начертить равносторонний треугольник

Из этого материала вы узнаете, как с помощью циркуля построить правильный треугольник. Напомним, что треугольник является правильным, если длина всех его сторон одинакова, а каждый из углов составляет 60°.

На листе бумаги отметьте произвольную точку. Установите в эту точку иглу циркуля и нарисуйте окружность.

Установите иглу циркуля в любую произвольную точку, лежащую на окружности, и нарисуйте вторую окружность с центром в этой точке.

При этом не меняйте раствор циркуля, то есть радиус первой окружности должен быть равен радиусу второй окружности.

Отметьте точки пересечения окружностей.

Соедините полученные точки линией. Полученный отрезок будет первой стороной треугольника.

Далее, через центры обеих окружностей нужно провести прямую линию.

Таким образом, у вас получилось три точки, которые будут тремя вершинами треугольника.

Соедините все три точки между собой.

Полученный треугольник имеет одинаковую длину сторон, а величина каждого его угла составляет 60°, а значит он правильный.

Содержание

Узнать ещё
Как нарисовать равносторонний треугольник
Прямоугольный треугольник. Теорема Пифагора.
теория по математике 📈 планиметрия
Свойства прямоугольного треугольника
Признаки равенства прямоугольных треугольников
Теорема Пифагора
Египетский треугольник
Пифагоровы тройки
🔍 Видео

Видео:№711. Начертите три треугольника: тупоугольный, прямоугольный и равносторонний. ДляСкачать

Узнать ещё

Знание — сила. Познавательная информация

Видео:Как построить равнобедренный или равносторонний треугольник по клеткам.Скачать

Как нарисовать равносторонний треугольник

Как нарисовать равносторонний треугольник, используя только линейку и карандаш? Этот способ позволяет быстро сделать рисунок правильного или равнобедренного треугольника.

Как нарисовать равнобедренный треугольник

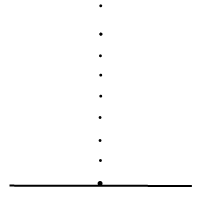
Рисунок начинаем с основания. Длину основания подбираем такой, чтобы ее удобно было делить пополам (берем четное количество клеточек). Вершину треугольника отмечаем ровно над серединой основания:

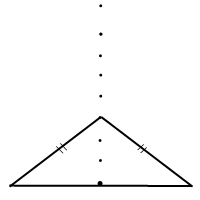
Если нужен равнобедренный треугольник, у которого боковая сторона больше основания, вершину ставим повыше:

Если требуется треугольник, основание которого больше боковой стороны, то вершину отмечаем ниже:

Как нарисовать равносторонний треугольник

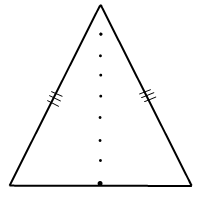
От конца основания откладываем отрезок равной ему длины так, чтобы второй конец этого отрезка расположился ровно над серединой основания. Соединяем вершину треугольника с другим концом основания:

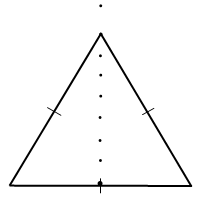
Если в задаче о равнобедренном треугольнике речь идет о высоте, биссектрисе и медиане, проведенным к основанию, достаточно соединить вершину треугольника с отмеченной серединой основания:

Видео:Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать

Прямоугольный треугольник. Теорема Пифагора.

теория по математике 📈 планиметрия

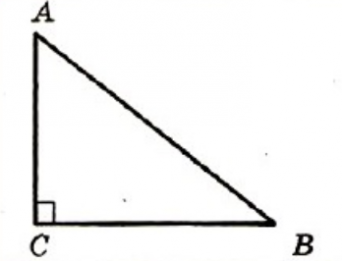
Если в треугольнике есть угол, равный 90 градусов, то такой треугольник называется прямоугольным. Стороны прямоугольного треугольника называются – катеты и гипотенуза. Катеты – это стороны, образующие прямой угол. Гипотенуза – сторона, которая располагается напротив прямого угла.

На рисунке треугольник АВС – прямоугольный, угол С равен 90º, стороны АС и ВС – катеты, а сторона АВ – гипотенуза.

Видео:КАК НАЧЕРТИТЬ РАВНОСТОРОННИЙ ТРЕУГОЛЬНИКСкачать

Свойства прямоугольного треугольника

В прямоугольном треугольнике гипотенуза является наибольшей стороной.
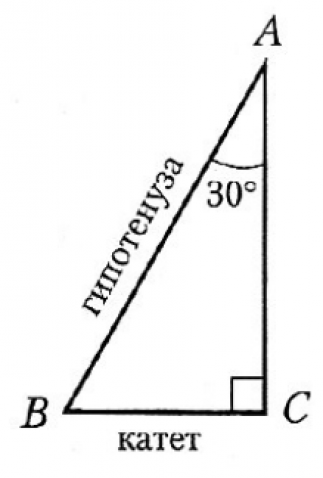
В прямоугольном треугольнике катет, лежащий напротив угла 30 0 , равен половине гипотенузы. И обратно, если катет равен половине гипотенузы, то угол, лежащий напротив этого катета, равен 30 0 .

Например, пусть угол А=30 0 , а гипотенуза АВ=28 см, то катет ВС будет равен 14 см, так как лежит напротив угла А=30 0 . Или, например, если катет ВС=6 см, а гипотенуза АВ равна 12 см, то угол А (лежащий напротив катета ВС), равен 30 0 .

Сумма острых углов прямоугольного треугольника равна всегда 90 градусов.
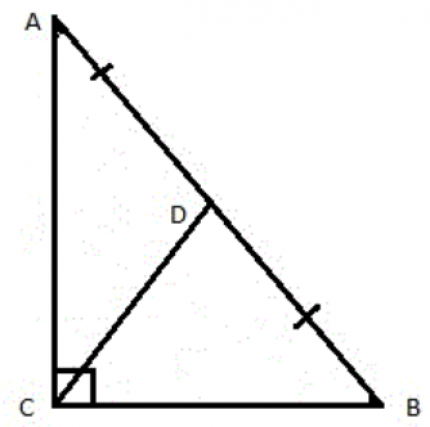
Медиана, проведенная к гипотенузе, равна её половине.

На рисунке изображен прямоугольный треугольник АВС, где CD – медиана, проведенная к гипотенузе. По свойству – медиана CD=0,5АВ, то есть AD=DB=CD.

Видео:Построение высоты в тупоугольном и прямоугольном треугольниках. 7 класс.Скачать

Признаки равенства прямоугольных треугольников

Существует 4 признака равенства прямоугольных треугольников:

Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны.
Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и острому углу другого прямоугольного треугольника, то такие треугольники равны.
Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.
Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны.

Чтобы быстрее запомнить данные признаки, можно использовать их краткую трактовку:

по катетам;
по катету и прилежащему острому углу;
по гипотенузе и острому углу;
по гипотенузе и катету.

Видео:7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

Теорема Пифагора

Древнегреческий философ, ученый, математик – Пифагор Самосский вывел теорему, которая до сих применима для решения задач. Теорема названа в честь него – «теорема Пифагора».

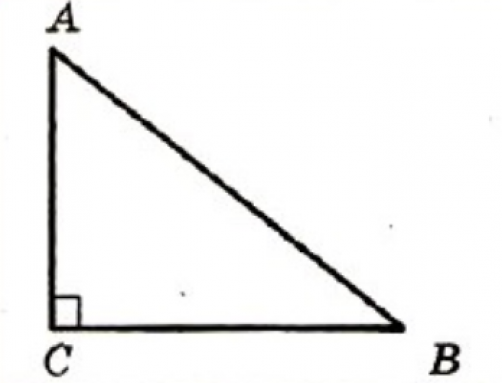
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

На рисунке в прямоугольном треугольнике АВ 2 =АС 2 +ВС 2

Например, если в данном треугольнике катеты равны 9 и 12 см, то можно найти длину гипотенузы, используя теорему: АВ 2 =9 2 +12 2 =81+144=225=15 2 , значит АВ=15 см.

Египетский треугольник

Треугольник со сторонами 3, 4 и 5 см называют Египетским треугольником.

Пифагоровы тройки

Тройки чисел, которые удовлетворяют теореме Пифагора, называют Пифагоровы тройки, а сами числа – Пифагоровы числа. Например, такими являются числа 16, 12 и 20 – это числа, которые при подстановке в формулу теоремы, дают нам верное равенство: 16 2 +12 2 =20 2 , 256+144=400, 400=400.