Сумма внешних углов треугольника

Внешний угол треугольника — это угол, смежный с любым из внутренних углов треугольника.

При каждой вершине треугольника может быть построено по два равных внешних угла. Например, если продолжить все стороны треугольника ABC, то при каждой его вершине получится по два внешних угла, которые равны между собой, как вертикальные углы:

Из данного примера можно сделать вывод, что внешние углы, построенные при одной вершине, будут равны.

Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.

Так как внешний угол (∠1) дополняет внутренний угол (∠4) до развёрнутого угла, то их сумма равна 180°:

Сумма внутренних углов углов любого треугольника тоже равна 180°, значит:

Из этого следует, что

Сократив обе части полученного равенства на одно и тоже число (∠4), получим:

Из этого можно сделать вывод, что внешний угол треугольника всегда больше любого внутреннего угла, не смежного с ним.

Видео:7 класс, 31 урок, Теорема о сумме углов треугольникаСкачать

Сумма внешних углов

Сумма трёх внешних углов треугольника, построенных при разных вершинах, равна 360°

Рассмотрим треугольник ABC:

Каждая пара углов (внутренний и смежный с ним внешний) в сумме равны 180°. Все шесть углов (3 внутренних и 3 внешних) вместе равны 540°:

(∠1 + ∠4) + (∠2 + ∠5) + (∠3 + ∠6) = 180° + 180° + 180° = 540°.

Значит чтобы найти сумму внешних углов, надо из общей суммы вычесть сумму внутренних углов:

∠1 + ∠2 + ∠3 = 540° — (∠4 + ∠5 + ∠6) = 540° — 180° = 360°.

Видео:Геометрия за 6 минут — Сумма углов треугольника и Внешний УголСкачать

Чему равна сумма внешних углов треугольника

Вопрос о том, чему равна сумма внешних углов треугольника, требует уточнения формулировки. Всего у треугольника есть шесть внешних углов — по два при каждой вершине.

Углы каждой пары равны между собой (как вертикальные):

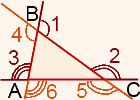
Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.

Отсюда сумма внешних углов треугольника, взятых по одному при каждой вершине, равна

Так как сумма углов треугольника равна 180º, то ∠А+∠В+∠С=180º. Значит, ∠1+∠2+∠3=2∙180º=360º.

Когда задают вопрос: «Чему равна сумма внешних углов треугольника?», чаще всего имеют в виду именно сумму углов, взятых по одному при каждой вершине. Поэтому следует уточнить формулировку — нужно найти сумму углов, взятых по одному при каждой вершине или сумму всех внешних углов. Сумма всех шести внешних углов, соответственно, в два раза больше: ∠1+∠2+∠3+∠4+∠5+∠6=2(∠1+∠2+∠3)=720º.

Видео:Внешний угол треугольникаСкачать

2 Comments

Спасибо за конкретную и доступную информацию!

Видео:Сумма углов треугольника. Геометрия 7 класс | МатематикаСкачать

Внешний угол треугольника

Внешний угол треугольника – это угол, смежный с любым из внутренних углов треугольника.

При каждой вершине треугольника может быть построено по два равных внешних угла. Например, если продолжить все стороны треугольника ABC, то при каждой его вершине получится по два внешних угла, которые равны между собой, как вертикальные углы:

Из данного примера можно сделать вывод, что внешние углы, построенные при одной вершине, будут равны ( как вертикальные).

Записываем в тетрадь:

Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.

Так как внешний угол (∠1) дополняет внутренний угол (∠4) до развёрнутого угла, то их сумма равна 180°:

Сумма внутренних углов углов любого треугольника тоже равна 180°, значит:

Из этого следует, что

Сократив обе части полученного равенства на одно и тоже число (∠4), получим:

Из этого можно сделать вывод, что внешний угол треугольника всегда больше любого внутреннего угла, не смежного с ним.

Видео:Геометрия 7 класс (Урок№23 - Сумма углов треугольника.)Скачать

Сумма внешних углов

Сумма трёх внешних углов треугольника, построенных при разных вершинах, равна 360°

Рассмотрим треугольник ABC:

Каждая пара углов (внутренний и смежный с ним внешний) в сумме равны 180°. Все шесть углов (3 внутренних и 3 внешних) вместе равны 540°:

(∠1 + ∠4) + (∠2 + ∠5) + (∠3 + ∠6) = 180° + 180° + 180° = 540°

Значит чтобы найти сумму внешних углов, надо из общей суммы вычесть сумму внутренних углов:

∠1 + ∠2 + ∠3 = 540° — (∠4 + ∠5 + ∠6) = 540° — 180° = 360°

Видео:Сумма внешних угловСкачать

Изучите видео ролик ниже:

Видео YouTube

Видео:Сумма внутренних углов многоугольника. Выпуклые и невыпуклые многоугольники. 8 класс.Скачать

Практическая часть занятий:

Видео:Сумма внешних углов треугольникаСкачать

Решение задач на отыскание величин треугольника по теореме о сумме углов треугольника и внешнем угле. Теоремы обязательно выучить и видео внимательно все разобрать:

Видео YouTube

📸 Видео

Чему равна сумма углов выпуклого многоугольникаСкачать

Теперь ты будешь находить углы за секунды. Как найти внешний угол треугольника? #математика #углыСкачать

Внешний угол треугольникаСкачать

№1082. Чему равна сумма внешних углов правильного n-угольника, если при каждой вершинеСкачать

ОГЭ Задание 25 Сумма внешних углов выпуклого многоугольникаСкачать

7 класс. Внешний угол треугольника.Скачать

Почему сумма углов треугольника 180 градусов?Скачать

Сумма внешних угловСкачать

Сумма углов треугольника равна 180Скачать

Сумма внешних углов выпуклого многоугольникаСкачать

Сумма углов треугольникаСкачать

Сумма внешних углов выпуклого многоугольникаСкачать