Как чертить окружность на чертеже

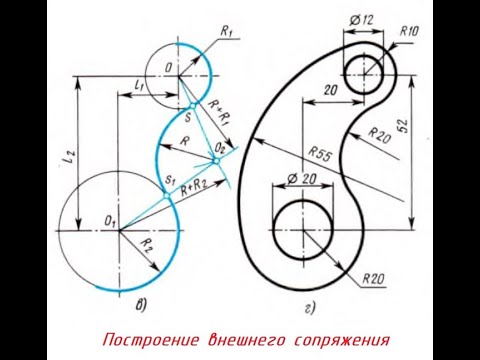
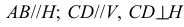Построение окружности:

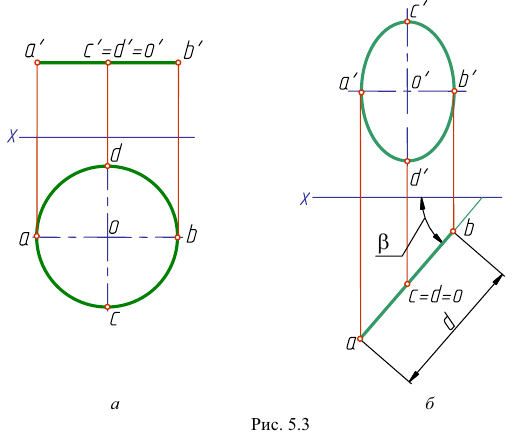
Окружность — плоская кривая второго порядка, ортогональная проекция которой может быть окружностью и эллипсом (рис. 5.3).

Для изображения окружности диаметра d на комплексном чертеже обязательно строят проекции центра О и двух ее диаметров.

Если окружность расположена в плоскости уровня, например в плоскости, параллельной плоскости Н (рис. 5.3, а), то в этом случае фронтальной проекцией окружности служит отрезок, равный d, а гори­ зонтальной проекцией является окружность.

Если окружность расположена в проецирующей плоскости, то проекции ее диаметров параллельны плоскостям проекций. Например,

Если окружность расположена в плоскости общего положения, она проецируется на все плоскости проекций в виде эллипсов, которые можно построить по сопряженным диаметрам. Эти диаметры являются проекциями диаметров, параллельных плоскостям проекций.

• Цилиндрическая винтовая линия
• Определение и задание поверхностей на чертеже
• Классификация поверхностей
• Пересечение многогранников плоскостями
• Взаимное положение двух плоскостей, прямой линии и плоскости
• Решение задач на тему: перпендикулярности прямой и плоскости
• Проекции с числовыми отметками
• Перспектива

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Видео:Как начертить овал. Эллипс вписанный в ромбСкачать

Чертеж круга, построение окружности в изометрии, формулы

Чертеж круга, построение окружности в изометрии прямоугольной по всем трем осевым направлениям X, Y, Z уменьшаются на восемнадцать процентов. По ГОСТу рекомендуют строить изометрическую проекцию по осям без сокращения. При таком построении происходит увеличение изображений в одну целую двадцать две сотых раза.

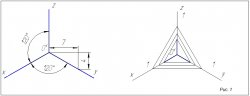
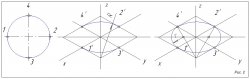
Посмотрим на 1-ый рисунок, как правильно располагать оси координат и наносить штриховку в прямоугольной изометрии.

На 2-ом рисунке посмотрим как правильно построить изометрическую проекцию окружности.

Если строим проекцию без искажения по трем осям X, Y, Z, значит большая ось эллипсов будет равняться 1,22, а малая – 0,71. Если строим проекцию с искажениями по трем осям X, Y, Z, значит большая ось эллипсов будет равняться диаметру (D), а малая – 0,58D.

На 3-ем рисунке показано как правильно располагать окружность на чертеже.

Чертеж круга и окружности.
Основным геометрическим размер окружности является прямой отрезок, который соединяет ее центр с точкой.

Условное обозначение R. Название радиус.

Смотрим 4-ый рисунок.

Множество точек, одинаково удаленных от центра на расстояние R описывают замкнутую плоскую кривую, которая и называется окружность.

Диаметр окружности обозначается D
D = 2R

Длина окружности обозначается С
С = 2πR = πD

π=С/D=3,141 592 653 589 793 … (трансцендентное число)

Множество точек, удаленных от центра на расстояние не превышающее R, называется кругом.

Площадь круга обозначается S
S = πR² = πD²/4

Вспомогательные формулы
С = 2√πS ≈ 3,545√S ≈ 3,142D
S = CD/4 ≈ 3,142 R² ≈ 0,785 D² ≈ 0,25CD
R = C/2π ≈ 0,159C
D = 2√S/π ≈ 1,128√S

Дополнительную информацию по геометрии смотрим на страницах сайта

Видео:1 2 4 сопряжение окружностейСкачать

Окружность

Окружность — это геометрическая фигура, образованная замкнутой кривой линией, все точки которой одинаково удалены от одной и той же точки.

Точка, от которой одинаково удалены все точки окружности, называется центром окружности. Центр окружности обычно обозначают большой латинской буквой O:

Окружность делит плоскость на две области — внутреннюю и внешнюю. Геометрическая фигура, ограниченная окружностью, — это круг:

Видео:Аксонометрические Проекции Окружности #черчение #окружность #проекции #изометрияСкачать

Построение окружности циркулем

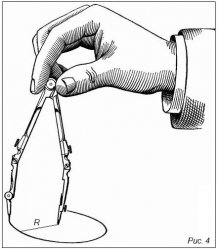
Для построения окружности используют специальный прибор — циркуль:

Установим циркулю произвольный раствор (расстояние между ножками циркуля) и, поставив его ножку с остриём в какую-нибудь точку плоскости (например, на листе бумаги), станем вращать циркуль вокруг этой точки. Другая его ножка, снабжённая карандашом или грифелем, прикасающимся к плоскости, начертит на плоскости замкнутую линию — окружность:

Видео:Построение эвольвенты окружностиСкачать

Радиус, хорда и диаметр

Радиус — это отрезок, соединяющий любую точку окружности с центром. Радиусом также называется расстояние от точки окружности до её центра:

Все радиусы окружности имеют одну и ту же длину, то есть они равны между собой. Радиус обозначается буквой R или r.

Хорда — это отрезок, соединяющий две точки окружности. Хорда, проходящая через центр, называется диаметром окружности.

Диаметр обозначается буквой D. Диаметр окружности в два раза больше её радиуса:

Дуга — это часть окружности, ограниченная двумя точками. Любые две точки делят окружность на две дуги:

Чтобы различать дуги, на которые две точки разделяют окружность, на каждую из дуг ставят дополнительную точку:

Для обозначения дуг используется символ :

• AFB — дуга с концами в точках A и B, содержащая точку F;
• AJB — дуга с концами в точках A и B, содержащая точку J.

О хорде, которая соединяет концы дуги, говорят, что она стягивает дугу.

Хорда AB стягивает дуги AFB и AJB.

📽️ Видео

Деление окружности на равные части. Урок 6. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Построение 8 угольника циркулемСкачать

КАК НАРИСОВАТЬ КРУГ В ИЗОМЕТРИИ (ОВАЛ В ИЗОМЕТРИЧЕСКОЙ ПРОЕКЦИИ).Скачать

Построение пятиугольника циркулемСкачать

Как начертить овал во фронтальной плоскостиСкачать

Деление окружности на пять равных частей. Урок 7. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

ПОСТРОЕНИЕ ОВАЛА │ КАК НАЧЕРТИТЬ ОВАЛ ПРИ ПОСТРОЕНИИ АКСОНОМЕТРИИ │ Урок #61Скачать

Построение 10 угольника циркулемСкачать

Радиус и диаметрСкачать

Как начертить цилиндр в объемеСкачать

Сопряжение двух пересекающихся прямых. Урок 9. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

2 2 3 построение изометрии окружностиСкачать

ПРИЕМЫ РАБОТЫ С ЧЕРТЕЖНЫМ ИНСТРУМЕНТОМ. Линии чертежа. Видео для начинающихСкачать

Как начертить овал в горизонтальной плоскостиСкачать

Черчение. Внутреннее, внешнее и смешенное сопряжение двух окружностей.Скачать

Построение ВНЕШНЕГО СОПРЯЖЕНИЯСкачать