Как провести биссектрису в треугольнике

Умение разделить любой угол биссектрисой нужно не только для того, чтобы получить «пятерку» по математике. Эти знания очень пригодятся строителю, дизайнеру, землемеру и портнихе. В жизни многое надо уметь делить пополам.

Все в школе учили шуточное определение про крысу, которая бегает по углам и делит угол пополам. Звали этого шустрого и умного грызуна Биссектрисой. Не известно, каким образом крыса делила угол, а для начинающих математиков в школьном учебнике «Геометрия» могут быть предложены следующие способы.

На них влияет магнитное склонение, которое зависит от положения на Земле. Они определяются на земле компасом. Как мы только что видели, инструментами, которые мы используем для определения направлений, являются гониометр или конвейер для картографического направления и компас для магнитного направления. Следует отметить, что в проекции Гаусса-Крюгера картографическое направление приближается к азимуту в окрестности авто-линии. Азимут может быть рассчитан путем измерения компаса на земле или конвейера на графике, если мы сделаем правильную коррекцию путем склонения и магнитного отклонения.

Видео:7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

С помощью транспортира

Видео:Высота, биссектриса, медиана. 7 класс.Скачать

С помощью циркуля

Видео:Построение биссектрисы в треугольникеСкачать

С помощью линейки

Видео:Построение биссектрисы углаСкачать

Без инструментов

Видео:Построение медианы в треугольникеСкачать

Развернутый угол

Видео:Построение высоты в треугольникеСкачать

Углы в треугольнике

Биссектрисой угла называют луч, который начинается в вершине угла и делит его на две равные части. Т.е. чтобы провести биссектрису , нужно найти середину угла . Наиболее простой способ это сделать — при помощи циркуля. В этом случае вам не нужно проводить никаких вычислений, и результат не будет зависеть от того, является ли величина угла целым числом.

Одна из особенностей заключается в том, что это направление постоянно меняется, когда вы путешествуете по маршруту. До этого нам приходилось довольствоваться прохождением лаксодромических направлений, для которых используется компас, но дорога была не кратчайшей. Самолеты были вынуждены, пока не так давно, пересечь полигоналы, чтобы попытаться приблизиться к ортодромической или более короткой дороге.

Направления определяются по-разному, в основном двух типов: инструментальные и неинструментальные. Считается, что следующие инструменты. Магнитный: используя компас в земле, определяя магнитные направления. Позднее мы увидим обработку компаса. Геометрический: используя гониометр или конвейер на графике, определяя картографические направления.

Видео:Построение биссектрисы углаСкачать

Вам понадобится

• циркуль, карандаш, линейка.

Видео:№102. Начертите треугольник. С помощью транспортира и линейки проведите его биссектрисы.Скачать

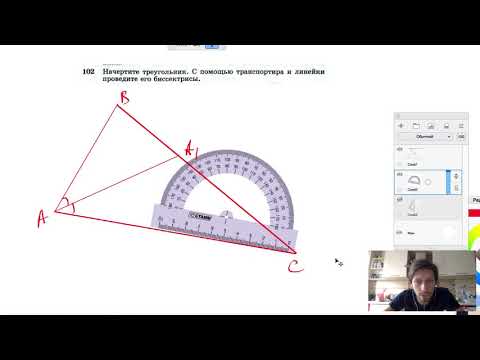
Инструкция

Установите иглу циркуля в вершину угла . Ширина раствора циркуля должна быть тем больше, чем тупее угол, для которого вы проводите биссектрису .

Отложите циркулем на каждой стороне угла по отрезку одинаковой длины. Чтобы отложить равные отрезки, достаточно не смещать иглу и не менять раствора циркуля.

Другие: они избегают нашего интереса, как инерционные методы, используемые самолетами с использованием гироскопов или радиомаяков. Классический способ ориентироваться в инструментах на природе — объединить использование буквы и конвейера с компасом. Это дает возможность «перевести» то, что мы измерили в письме, местности и наоборот. В основном он состоит из следующего.

Нарисуйте прямую линию на графике, соединяя начальную точку с желаемым пунктом назначения. Конвейер размещается с центром над пересечением линии или ее продолжением и меридианом. Конвейер поворачивается, пока нуль не совпадает с северным направлением меридиана.

Оставив ширину раствора циркуля прежней, установите иглу в конце отрезка на одной из сторон и начертите часть окружности так, чтобы она располагалась внутри угла . То же самое сделайте и со второй стороны. У вас получится две части окружностей, которые будут пересекаться внутри угла — примерно посередине. Пересекаться части окружностей могут в одной или двух точках.

С луной существует быстрый и грубый метод, основанный на фазах. На самом деле это вариант использования солнца. Он широко известен как метод часов и очень распространен. Проблема в том, что не так широко распространена очень низкая точность, которую она может дать в некоторых случаях. Поэтому здесь мы ограничимся тем, что будем описывать это больше всего, чтобы советовать ему советовать. То, как мы описываем, — это книга, которую цитируют книги для южного полушария. Это также неточно: он работает только для субтропических регионов южного полушария, для южного тропического он работает с меньшей точностью и только между равноденствием с марта по сентябрь.

Он считывает угловое значение, которое обозначает линию, первоначально нарисованную на конвейере. Это направление корректируется путем добавления или вычитания локального магнитного склонения, таким образом, получения курса. Мы увидим эту операцию позже.

Он «записывает» это направление в конечности компаса, если он является моделью, которая позволяет оставить лимбоблокировку в позиции курса. Если это тарелка, ожидается, что баланс будет сбалансирован, а ценность подшипника на шкале будет запрошена с помощью системы прицеливания.

Для этих операций компас должен быть в идеальном балансе и горизонтали. Затем стрелка или ось направления компаса указывают в следующем порядке. Точка интереса на земле указана на компас. Эта операция зависит от типа компаса. В одной из игл мы должны сделать, чтобы совпасть до того, как проделать 0º с севера иглы. В одном из блюд достаточно прочитать курс, который обозначает индикатор.

От вершины угла через точку пересечения окружностей начертите луч. В случае, если у вас получилось две точки пересечения окружностей, он должен проходить через обе. Полученный луч и будет являться биссектрисой данного угла .

Для построения биссектрисы угла можно использовать транспортир, но этот способ требует большей точности. При этом, если величина угла не будет являться целым числом, вероятность погрешностей в построении биссектрисы возрастает.

Курс преобразуется в азимут путем локального склонения. Затем он поворачивается так, что направление 0º — 180º совпадает с меридианом или 90º — 270º с параллелью. Участок, обозначающий угловое значение, найденное на конвейерной шкале, обозначается точкой.

Наша цель теперь будет нарисованной линии в смысле объективного момента, если мы сосредоточимся на нашей позиции, или наоборот. Мы можем исследовать эту линию, сравнивая то, что мы видим под ней в письме, и то, что показывает нам рельеф. Это подробно видно на курсах.

Этот факт не заменяет классический инструмент ориентации, а дополняет его. Это позволяет отключить электронное устройство и сэкономить время и энергию. Кроме того, в случае отказа или сбоя питания электронного устройства компас всегда будет продолжать работать.

Углом называется геометрическая фигура, которая образована двумя лучами – сторонами угла, исходящими из одной точки – вершины угла. Обычно для построения плоского угла в планиметрии используется транспортир, с помощью которого можно легко отложить угол с заданной градусной мерой, но как быть, если под рукой этого инструмента нет?Для построения угла можно воспользоваться тригонометрическими функциями и построением прямоугол ьного треугол ьника.

Когда у нас нет конкретных инструментов, как описано выше, некоторые импровизации и наблюдения природы позволяют нам ориентироваться с некоторой независимостью. Существует два типа неинтерактивного метода. Рациональное: когда есть научная основа, которая гарантирует точность и точность мер. Обычно это астрономические методы. Звезды всегда были типичным методом ориентации и навигации и единственными доступными для позиции. Здесь мы увидим только самые полевые методы, очевидно, не попадая в использование звезд, где требуются специальные инструменты, как в случае с навигацией, использующей секстанты, астролябии и другие материалы.

• Полная таблица тангенсов, линейка

Пусть стоит задача построить угол некоторой размерности?.
Построим отрезок AB произвольной длины. Использую соотношение катетов в прямоугол ьном треугол ьнике можно получить сторону BC этого треугол ьника по формуле BC = AB tg?, значение тангенса угла? можно узнать по таблице тангенсов .
Далее от точки A необходимо отложить отрезок длины BC перпендикулярно отрезку AB.

Эмпирический: когда научное пропитание слабее или замаскировано многими переменными. Таков случай направлений роста растений, доминирующих ветров, орографии и т.д. Самый быстрый и простой способ заключается в следующем. Палка, палочка, карандаш или любой другой заостренный элемент размещаются на определенной высоте на земле. Он не должен быть вертикальным: его можно разместить горизонтально на скале, например. Это также может быть остроконечная скала. Условием является то, что он проецирует свою тень на гладкую поверхность, плоскую и горизонтальную.

Соединив точки A и C, получим угол заданной величины?, с вершиной в точке A.

Обратите внимание, что должны выполняться три условия: гладкий — это не то же самое, что и плоскость, а плоскость не совпадает с горизонтальной. Эту поверхность можно получить, поместив лист бумаги, блюдо или камень на место или сгладьте землю рукой. Он не требует гораздо большего размера, чем ладонь. Другое условие заключается в том, что тень резкого конца объекта острая. Это достигается путем размещения элемента на не слишком большом расстоянии от плоскости. Не слишком близко, потому что, как мы увидим, требуется, чтобы тень «двигалась» на определенное расстояние, когда солнце или луна пробегали от влияния вращения Земли.

Для построения углов ∠α ≥ 90º, необходимо построить угол ∠β

Биссектрисой угла называют луч, который начинается в вершине угла и делит его на две равные части. Т.е. чтобы провести биссектрису , нужно найти середину угла . Наиболее простой способ это сделать — при помощи циркуля. В этом случае вам не нужно проводить никаких вычислений, и результат не будет зависеть от того, является ли величина угла целым числом.

Хорошее расстояние — от 1 до 1, 5 метров. Знак делается в точке, где падает тень остроконечного конца объекта. Это можно сделать карандашом или просто прибивать зубочисткой или класть камешек. Ожидается, что тень будет двигаться из-за вращения Земли. Всего несколько сантиметров.

Точка тени снова обозначается на плоскости. Между двумя метками рисуется линия. Конец линии, которая находится в первом знаке, — Запад. Это так в любом полушарии, в любое время суток и в любое время года, хотя оно более чувствительно в низких широтах, около полудня и летом. Эти чувствительности очень скомпенсированы, если мы будем осторожны, чтобы быть ближе к полудню, то есть, если мы находимся в высоких широтах, более важно делать измерения в течение дня, избегая раннего утра или сумерек.

Установите иглу циркуля в вершину угла . Ширина раствора циркуля должна быть тем больше, чем тупее угол, для которого вы проводите биссектрису .

Отложите циркулем на каждой стороне угла по отрезку одинаковой длины. Чтобы отложить равные отрезки, достаточно не смещать иглу и не менять раствора циркуля.

Этот метод хорошо работает с луной и вряд ли чувствителен к широте или времени года, но лучше всего делать это с высокой луной над горизонтом. Другой метод намного точнее. Настолько, что это позволяет нам рассчитать магнитное склонение места, и если мы применим его с солнцем, мы получим очень полезную информацию для вычисления широты и длины с очень простыми формулировками с использованием двух таблиц, которые мы можем сделать фотокопированными в кошельке. Как длинный метод, так и эти дополнительные методы не будут разработаны в этом резюме.

Оставив ширину раствора циркуля прежней, установите иглу в конце отрезка на одной из сторон и начертите часть окружности так, чтобы она располагалась внутри угла . То же самое сделайте и со второй стороны. У вас получится две части окружностей, которые будут пересекаться внутри угла — примерно посередине. Пересекаться части окружностей могут в одной или двух точках.

С луной существует быстрый и грубый метод, основанный на фазах. На самом деле это вариант использования солнца. Он широко известен как метод часов и очень распространен. Проблема в том, что не так широко распространена очень низкая точность, которую она может дать в некоторых случаях. Поэтому здесь мы ограничимся тем, что будем описывать это больше всего, чтобы советовать ему советовать. То, как мы описываем, — это книга, которую цитируют книги для южного полушария. Это также неточно: он работает только для субтропических регионов южного полушария, для южного тропического он работает с меньшей точностью и только между равноденствием с марта по сентябрь.

Он считывает угловое значение, которое обозначает линию, первоначально нарисованную на конвейере. Это направление корректируется путем добавления или вычитания локального магнитного склонения, таким образом, получения курса. Мы увидим эту операцию позже.

Он «записывает» это направление в конечности компаса, если он является моделью, которая позволяет оставить лимбоблокировку в позиции курса. Если это тарелка, ожидается, что баланс будет сбалансирован, а ценность подшипника на шкале будет запрошена с помощью системы прицеливания.

Для этих операций компас должен быть в идеальном балансе и горизонтали. Затем стрелка или ось направления компаса указывают в следующем порядке. Точка интереса на земле указана на компас. Эта операция зависит от типа компаса. В одной из игл мы должны сделать, чтобы совпасть до того, как проделать 0º с севера иглы. В одном из блюд достаточно прочитать курс, который обозначает индикатор.

От вершины угла через точку пересечения окружностей начертите луч. В случае, если у вас получилось две точки пересечения окружностей, он должен проходить через обе. Полученный луч и будет являться биссектрисой данного угла .

Мы назвали его методом солнечного времени, а не часами, потому что это можно сделать без часов. Достаточно нарисовать часы и руки на земле или на бумаге. Некоторые неумные источники заявляют, что это можно сделать только с аналоговыми часами, а не с цифровыми часами, когда на самом деле очень легко нарисовать часы, если время известно. Другая причина ставить солнечное время, а не просто время, заключается в том, что метод строго работает с солнечным временем, а не с гражданским временем.

Часы установлены с горизонтальной сферой, а 12 — на солнце. Это достигается путем установки вертикальной палочки на 12 и поворота набора до тех пор, пока тень не упадет на. Биссектриса между 12 и маленькой рукой указывает на Север. В той степени, в которой в стране солнечный полдень не достигнут 12, этот метод даст нам ошибку приблизительно 7º за каждый час разницы. Это было особенно заметно во времена, когда Аргентина использовала другое время летом. В этом случае в горной части Мендоцина солнечный полдень был выпущен почти в 3 часа ночи!

Для построения биссектрисы угла можно использовать транспортир, но этот способ требует большей точности. При этом, если величина угла не будет являться целым числом, вероятность погрешностей в построении биссектрисы возрастает.

При строительстве или разработке домашних дизайн-проектов часто требуется построить угол , равный уже имеющемуся. На помощь приходят шаблоны и школьные знания геометрии.

Короче: мы должны взять компас или ориентироваться с тенью и солнцем. В северном полушарии есть звезда, полярная звезда, которая почти точно находится на северном небесном полюсе, хотя она очень мало яркая. Небесные полюса — это точки неба, где проецируется ось земного вращения. В вертикали, перпендикулярной к горизонту, от небесного полюса есть кардинальная точка, северная или южная.

В Южном полушарии у нас нет звезд на полюсе Южного Севера, поэтому мы должны сделать геометрическую конструкцию с созвездиями. Для этого мы используем созвездие Крукс, представляющее собой созвездие 5 звезд, видимых в южном полушарии, следующим образом.

Угол образуют две прямые, исходящие из одной точки. Эта точка будет называться вершиной угла, а линии будут являться сторонами угла.

Для обозначения углов используйте три буквы: одна у вершины, две у сторон. Называют угол , начиная с той буквы, которая стоит у одной стороны, далее называют букву, стоящую у вершины, и затем букву у другой стороны. Используйте и другие способы для обозначения углов, если вам удобнее иначе. Иногда называют только одну букву, которая стоит у вершины. А можно обозначать углы греческими буквами, например, α, β, γ.

Представьте себе крест, начертанный четырьмя яркими звездами Крукса. Увеличьте большую длину креста в направлении основного плеча 5 раз, а результирующая точка 1 больше перпендикулярно правую. Важно, чтобы последние были хорошо поняты: перпендикулярно переднему и правому направлениям переднего направления. Этот второй более короткий сегмент, в зависимости от положения креста, может падать вправо или влево, вверх или вниз.

Полученная таким образом конечная точка является небесным южным полюсом. Спустившись по перпендикуляру к горизонту с небесного южного полюса, получим направление Юг. Другой способ найти небесный Южный полюс — это точка, которая находится на полпути между звездой Ачернар и Бета Центаури. Другой известный метод, который является кинжалом Ориона, не очень точен в Южном полушарии.

Встречаются ситуации, когда необходимо начертить угол , чтобы он был равен уже данному углу. Если при построении чертежа использовать транспортир возможности нет, можно обойтись только линейкой и циркулем. Допустим, на прямой, обозначенной на чертеже буквами MN, нужно построить угол у точки К, так, чтобы он был равен углу В. То есть из точки K необходимо провести прямую, образующую с линией MN угол , который будет равен углу В.

Для начинающих математиков в школьном учебнике «Геометрия» могут быть предложены следующие способы.

Видео:Биссектрисы треугольника.Скачать

С помощью транспортира

Видео:Геометрия 7 класс (Урок№12 - Медианы треугольника. Биссектрисы треугольника. Высоты треугольника.)Скачать

С помощью циркуля

Видео:Построение высоты в тупоугольном и прямоугольном треугольниках. 7 класс.Скачать

С помощью линейки

Видео:Как построить биссектрису, медиану и высоту в треугольникеСкачать

Без инструментов

Видео:Построение биссектрисы угла. 7 класс.Скачать

Развернутый угол

Угол больше 180 градусов можно разделить биссектрисой такими же способами. Только делить надо будет не его, а прилежащий к нему острый угол, оставшийся от окружности. Продолжение найденной биссектрисы и станет искомой прямой, делящей развернутый угол пополам.

Видео:№154. Дан треугольник ABC. Постройте: а) биссектрису АК; б) медиану ВМ; в) высоту СН треугольника.Скачать

Как можно построить биссектрису угла с помощью циркуля и линейки?

Видео:Биссектриса треугольника. Построение. 1 частьСкачать

Процесс построения

Биссектриса (лат. bisectio) представляет собой геометрическое место точек внутри угла (острый, прямой или тупой), которые одинаково удалены от обеих его сторон.

Для её построения нужно подготовить различные школьные принадлежности и выполнить несколько простых действий.

Подготовительный этап

Чтобы быстро найти биссектрису треугольника с помощью циркуля, нужно провести тщательную подготовку. Она заключается в поиске школьных принадлежностей, которые будут использоваться при построении.

Необходимые предметы:

Порядок действий

Нарисовать луч, разделяющий пополам угол, можно при помощи транспортира. Однако если этой школьной принадлежности нет в наличии, заменить её сможет обыкновенный циркуль.

Быстрый способ:

1. На листе бумаги рисуют 2 пересекающиеся линии.
2. Чтобы построить биссектрису данного угла, в его вершину ставят ножку циркуля и чертят окружность произвольного радиуса.
3. Отмечают точками места пересечения сторон угла с окружностью.
4. На них поочерёдно ставят циркуль и, не меняя радиус, рисуют 2 дуги.
5. Находят и отмечают место их пересечения.
6. Стирают дуги ластиком, чтобы они не мешали дальнейшей работе.
7. С помощью линейки и простого карандаша проводят искомый отрезок, соединяющий вершину угла с точкой пересечения дуг.

С помощью циркуля можно легко найти биссектрису треугольника (всякого). Для этого понадобится стандартный набор школьных принадлежностей и наличие базовых знаний геометрии.

Порядок действий:

1. Любым известным способом вписывают окружность в треугольник.
2. С помощью карандаша и линейки из её центра проводят линии к каждой вершине.
3. Полученные отрезки станут частью искомого луча.

Видео:Построить биссектрису угла. Построение с помощью циркуля и линейки.Скачать

Альтернативный вариант

Если у ученика нет циркуля, то начертить луч, разделяющий угол пополам, можно и без этой школьной принадлежности. Для работы понадобится линейка, карандаш и транспортир.

Правильная последовательность действий:

1. Нулевое значение на шкале прикладывают к вершине.
2. Совмещают линейку транспортира с одним из лучей и определяют величину угла.
3. Полученное значение делят пополам.
4. Затем заново прикладывают транспортир и откладывают величину, полученную в результате расчётов.
5. Через эту точку и вершину проводят отрезок, который будет являться искомым лучом.

Видео:Формула для биссектрисы треугольникаСкачать

Полезные советы

В некоторых случаях для нахождения не нужно использовать транспортир и циркуль. Это возможно только тогда, когда нужно определить расположение биссектрисы в треугольнике.

Полезные рекомендации:

1. Биссектриса всегда разделяет противолежащую сторону треугольника в отношении, равном пропорции 2 других сторон геометрической фигуры.
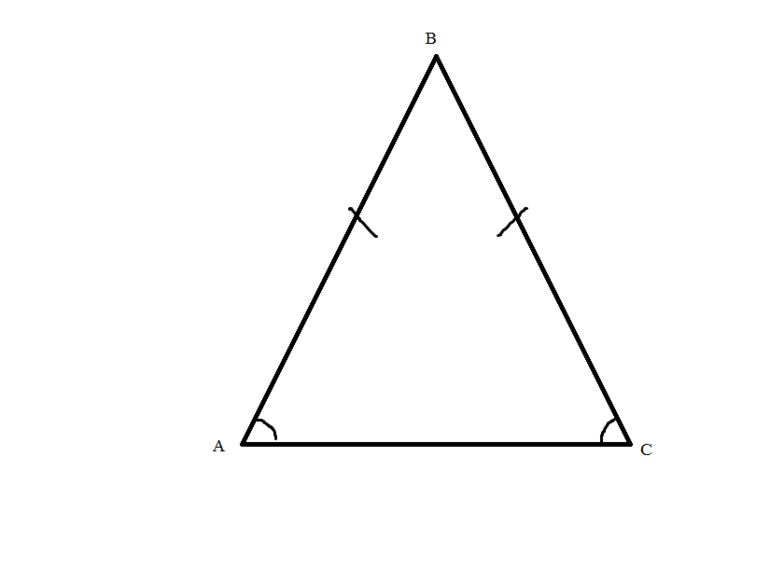
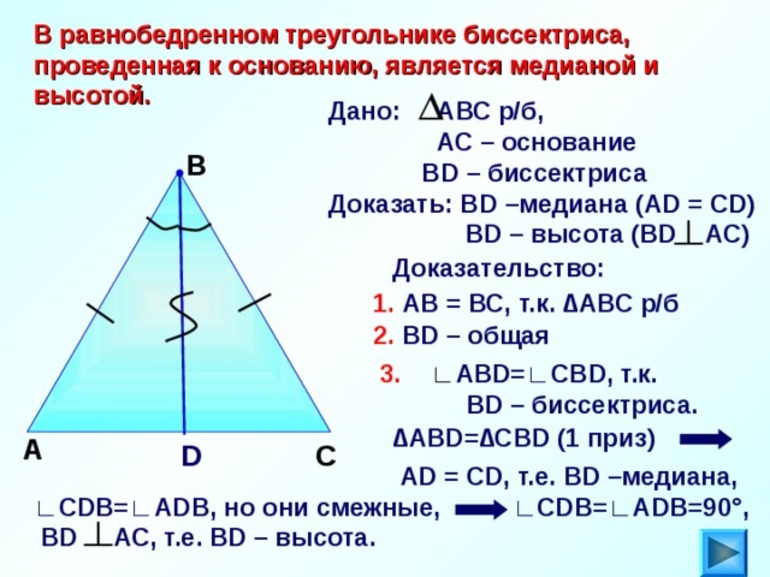
2. В равнобедренном треугольнике биссектрисы всегда пересекаются под прямым углом.
3. Если треугольник равносторонний, то все биссектрисы будут параллельны противоположным сторонам. При этом длина образованных отрезков будет одинаковой.

Построить биссектрису угла с помощью циркуля сможет даже двоечник. Для этого ему понадобится минимум времени, знаний и усилий. Подробно изучив порядок действий, каждый учащийся сможет легко поделить любой угол пополам и объяснить этот процесс одноклассникам.

Видео:Высоты треугольника.Скачать

Определение и свойства биссектрисы угла треугольника

В данной публикации мы рассмотрим определение и основные свойства биссектрисы угла треугольника, а также приведем пример решения задачи, чтобы закрепить представленный материал.

Видео:Как найти биссектрису в треугольнике? 2 формулы биссектрисыСкачать

Определение биссектрисы угла треугольника

Биссектриса угла – это луч, который берет начала в вершине угла и делит данный угол пополам.

Биссектриса треугольника – это отрезок, соединяющий вершину угла треугольника с противоположной стороной и делящий этот угол на две равные части. Такая биссектриса, также, называется внутренней.

Основание биссектрисы – точка на стороне треугольника, которую пересекает биссектриса. Т.е. в нашем случае – это точка D.

Внешней называется биссектриса угла, смежного с внутренним углом треугольника.

Видео:Высота медиана биссектриса в тупоугольном треугольникеСкачать

Свойства биссектрисы треугольника

Свойство 1 (теорема о биссектрисе)

Биссектриса угла треугольника делит его противоположную сторону в пропорции, равной отношению прилежащих к данному углу сторон. Т.е. для нашего треугольника (см. самый верхний рисунок):

Свойство 2

Точка пересечения трех внутренних биссектрис любого треугольника (называется инцентром) является центром вписанной в фигуру окружности.

Свойство 3

Все биссектрисы треугольника в точке пересечения делятся в отношении, равном сумме прилежащих к углу сторон, деленной на противолежащую сторону (считая от вершины).

Свойство 4

Если известны длины отрезков, образованных на стороне, которую пересекает биссектриса, а также две другие стороны треугольника, найти длину биссектрисы можно по формуле ниже (следует из теоремы Стюарта):

BD 2 = AB ⋅ BC – AD ⋅ DC

Свойство 5

Внешняя и внутренняя биссектрисы одного и того же угла треугольника перпендикулярны друг к другу.

• CD – внутренняя биссектриса ∠ACB;
• CE – биссектриса угла, смежного с ∠ACB;
• ∠DCE равен 90°, т.е. биссектрисы CD и CE перпендикулярны.

Пример задачи

Дан прямоугольный треугольник с катетами 6 см и 8 см. Найдите длину биссектрисы, проведенной к гипотенузе.

Решение
Нарисуем чертеж согласно условиям задачи.

Применив теорему Пифагора мы можем найти длину гипотенузы (ее квадрат равен сумме квадратов двух катетов).
BC 2 = AB 2 + AC 2 = 6 2 + 8 2 = 100.
Следовательно, BC = 10 см.

Далее составляем пропорцию согласно Свойству 1, условно приняв отрезок BD на гипотенузе за “a” (тогда DC = “10-a”):

Избавляемся от дробей и решаем получившееся уравнение:
8a = 60 – 6a
14a = 60
a ≈ 4,29

Таким образом, BD ≈ 4,29 см, CD ≈ 10 – 4,29 ≈ 5,71 см.

Теперь мы можем вычислить длину биссектрисы, использую формулу, приведенную в Свойстве 4:
AD 2 = AB ⋅ AC – BD ⋅ DC = 6 ⋅ 8 – 4,29 ⋅ 5,71 ≈ 23,5.