К окружности вписанной в равносторонний треугольник проведена касательная которая пересекает

Видео:Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать

Условие

К окружности, вписанной в правильный треугольник ABC , проведена касательная, пересекающая стороны AC и BC в точках M и N соответственно и касающаяся окружности в точке T .

а) Докажите, что периметр треугольника MNC равен стороне треугольника ABC .

б) Найдите MT:TN, если известно, что CM: MA=1:4.

Видео:САМЫЙ СТРАННЫЙ ПРИМЕР 3 задания проф. ЕГЭ по математикеСкачать

Решение

а) Пусть K и L — точки касания окружности и сторон BC и AC соответственно.

Так как MT=ML и NK=NT как отрезки касательных, проведенных из одной точки, то

P_= CM+MT+TN+NC= CM+ML+KN+NC= CL+KC.

Так как ABC — правильный треугольник, то CL=KC=frac. Следовательно, P_=AC, что и требовалось доказать.

б) 1 . Обозначим TN=x, CM=a. Так как CM:MA=1:4 по условию, то MA=4a и AC=5a.

Тогда CL=frac=fraca и ML=CL-CM=fraca-a=fraca. Так как ML=MT, то MT=fraca. Тогда MN=MT+TN=fraca+x.

Так как NT=NK, то NK=x. Тогда CN=CK-NK=frac-x=fraca-x.

2. По теореме косинусов для треугольника MNC

MN^2=CN^2+CM^2- 2 cdot CN cdot CM cdot cos angle NCM. Подставляя в это уравнение выражения для сторон треугольника MNC , получим:

left ( fraca+xright )^2= left ( fraca-xright )^2+a^2-2left ( fraca-xright )a cos 60^circ;

fraca^2+2 cdot fracax+x^2= fraca^2-2 cdot fracax+x^2+a^2- 2left ( fraca-x right )a cdot frac;

Видео:Решение задачи №1 из ЕГЭ математикаСкачать

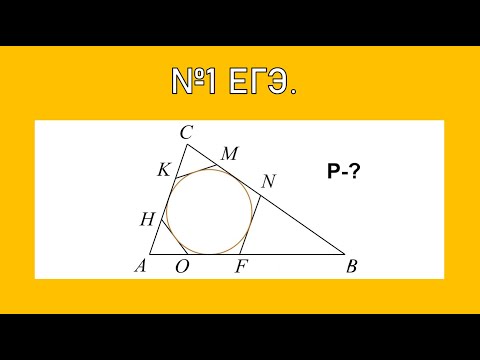
К окружности, вписанной в равносторонний треугольник со стороной а, проведения касательной, которая пересекает две стороны треугольника. Найдите периметр

Видео:Окружность вписана в равносторонний треугольник, найти радиусСкачать

Ваш ответ

Видео:Геометрия. ОГЭ по математике. Задание 16Скачать

решение вопроса

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Похожие вопросы

• Все категории
• экономические 43,283
• гуманитарные 33,619
• юридические 17,900
• школьный раздел 607,073
• разное 16,829

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Помогите плз )к окружности, вписанной в равносторонний треугольник со стороной 6 , проведена касательная, пересекающая две его стороны?

Геометрия | 5 — 9 классы

Помогите плз )к окружности, вписанной в равносторонний треугольник со стороной 6 , проведена касательная, пересекающая две его стороны.

Найти периметр отсеченного треугольника

Треугольник АВС, АВ = ВС = АС = 6, радиус вписанной = сторона * корень3 / 6 = 6 * корень3 / 6 = корень3, ТК касательная , Т — точка пересечения с АВ, К — пересечение с ВС, считаем что ТК параллельна АС (другие случаи не рассматриваем, а вообще — то рисунок есть?

, как она касательная проходит?

), проводим радиусы пенрпендикулярные в точки касания, ОЕ — на АВ, ОМ — на ВС, ОН — на ТК, уголЕОМ = 360 — 90 — 90 — уголВ = 360 — 90 — 90 — 60 = 120, ОВ биссектриса угла : ЕОМ и угла В, уголНОМ = 1 / 2углаЕОМ = 120 / 2 = 60, проводим ОК, треугольник ОНК = треугольник КОМ как прямоугольные по катету (ОН = ОМ = радиус) и гипотенузе ОК — общая уголНОК = уголКОМ = уголНОМ / 2 = 60 / 2 = 30, АМ — медиана, высота, биссектриса, ВМ = СМ = ВС / 2 = 6 / 2 = 3, НК = КМ как касательные проведенные из одной точки, НК = КМ = ОН * tg30 = корень3 * корень3 / 3 = 1, ВК = ВМ — КМ = 3 — 1 = 2 = ВТ, НК = НТ = 1, ТК = 1 + 1 = 2, периметр ТВК = 2 + 2 + 2 = 6.

Видео:Окружность, вписанная в треугольникСкачать

В равностороннем треугольнике вписана окружность радиусом 8 см?

В равностороннем треугольнике вписана окружность радиусом 8 см.

Найти сторону треугольника.

Видео:Математика за минуту: Объяснение формулы радиуса вписанной окружности в прямоугольный треугольник.Скачать

В равносторонний треугольник вписанный окружности радиусом 8 см?

В равносторонний треугольник вписанный окружности радиусом 8 см.

Найти сторону треугольника.

Видео:Формулы для радиуса окружности #shortsСкачать

Равносторонний треугольник ABC вписан в окружность радиуса 6 см найти сторону треугольника?

Равносторонний треугольник ABC вписан в окружность радиуса 6 см найти сторону треугольника.

Видео:Задание 16 ОГЭ по математике. Окружность вписана в равносторонний треугольник.Скачать

Радиус окружности, вписанной в равносторонний треугольник, равен см?

Радиус окружности, вписанной в равносторонний треугольник, равен см.

Найти сторону треугольника.

Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Равносторонний треугольник MNK со стороной 8 см, вписан в окружность?

Равносторонний треугольник MNK со стороной 8 см, вписан в окружность.

Видео:Геометрия. ОГЭ по математике. Задание 16Скачать

Равносторонний треугольник MNK со стороной 8 см, вписан в окружность?

Равносторонний треугольник MNK со стороной 8 см, вписан в окружность.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Помогите?

Равносторонний треугольник АВС вписан в окружность радиуом 6 см.

Видео:✓ Простое решение красивой геометрии | Планиметрия | Физтех-2021. Математика | Борис ТрушинСкачать

В равносторонний треугольник вписана окружность?

В равносторонний треугольник вписана окружность.

Длина стороны треугольника 2 корня из 3.

Нужно найти радиус вписанной окружности.

Видео:Задача 6 №27910 ЕГЭ по математике. Урок 130Скачать

Равносторонний треугольник вписан в окружность с радиусом 6 см?

Равносторонний треугольник вписан в окружность с радиусом 6 см.

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

СРОЧНО ПОМОГИТЕ ?

Основание равнобедренного треугольника равно 4 см а боковые стороны по 10 см .

В треугольнике вписана окружность , а к этой окружности проведена касательная , которая пересекает боковые стороны .

Найдите периметр треугольника , который отсекает касательная.

Вы зашли на страницу вопроса Помогите плз )к окружности, вписанной в равносторонний треугольник со стороной 6 , проведена касательная, пересекающая две его стороны?, который относится к категории Геометрия. По уровню сложности вопрос соответствует учебной программе для учащихся 5 — 9 классов. В этой же категории вы найдете ответ и на другие, похожие вопросы по теме, найти который можно с помощью автоматической системы «умный поиск». Интересную информацию можно найти в комментариях-ответах пользователей, с которыми есть обратная связь для обсуждения темы. Если предложенные варианты ответов не удовлетворяют, создайте свой вариант запроса в верхней строке.

Подлежащие — одна черта, Сказуемое — две черты обстоятельство — точка пунктир Дополнение — пунктир.

Подлежащее одной чертой, сказуемое двумя, обстоятельство : _. _. _. В общем обстоятельство точка — тире, а дополнение пунктирной линией : — — — -.

Решение задачи во вложенном файле.

В прямоугольном ∆ АВС∠С = 90°, высота СК делит гипотенузу на отрезки АВ = 5 см, кВ = 1 см. Определите длину высоты СК. Высотапрямоугольноготреугольника, проведеннаяк гипотенузе, естьсреднеегеометрическое (среднеепропорциональное) между отрезками, н..

Так наверное, но это не точно)0).

Вот как то так этт 1.

1) Треугольники А2КВ2 и А1КВ1 подобны, так как плоскости α и β параллельны (дано), значит и отрезки А1В1 и А2В2 параллельны. Из подобия имеем : А2В2 / А1В1 = КВ2 / КВ1 = 9 / 4. Отсюда КВ2 = 18см. Тогда В1В2 = КВ2 — КВ1 или В1В2 = 18 — 8 = 10см. О..

По теореме Пифагора BD ^ 2 = BC ^ 2 + CD ^ 2. BD ^ 2 = 4x ^ 2 — x ^ 2. BD ^ 2 = 3x ^ 2BD = x корней из 3. Но CD ^ 2 = BD * AD. X ^ 2 = x корней из 3 * AD. AD = (х корей из 3) / 3. АВ = х корней их 3 + (х корней из 3) / 3 = (4х корней из 3) / 3.

📽️ Видео

Задача по геометрии.Скачать

Геометрия К окружности, вписанной в треугольник ABC, проведены три касательные (см. рис.)Скачать

Урок по теме ВПИСАННАЯ ОКРУЖНОСТЬСкачать