Если из точки вне окружности проведены к ней касательная и секущая , то произведение секущей на её внешнюю часть равно квадрату касательной. Вот наша окружность, вот точка A вне окружности, вот секущая AD, вот её внешняя часть AC, и вот касательная AB. И нам надо доказать, что AD*AC=AB^2. Чтобы доказать, проведём две хорды BC и BD и рассмотрим получившиеся треугольники ABC и ABD. Они подобны , т.к. у них один угол общий — угол A, и два равных угла с зубчиками: угол BDA вписанный , а угол CBA образован касательной и хордой, и оба угла измеряются половиной общей дуги с зубчиками. Составим пропорцию из соответственных сторон: то есть запишем равенство отношений длинной стороны к стороне, лежащей против зубастого угла: AD/AB=AB/AC. Это равенство равносильно тому, которое и требовалось доказать.
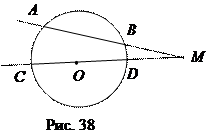
- Теорема 1. Произведение секущей, проведённой через точку М вне круга, на её внешнюю часть есть величина постоянная
- Из точки вне окружности проведена секущая, пересекающая окружность в точках, удаленных от данной на 24 см и 40 см. Расстояние от данной точки
- Ваш ответ
- решение вопроса
- Похожие вопросы
- 🎬 Видео
Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Теорема 1. Произведение секущей, проведённой через точку М вне круга, на её внешнюю часть есть величина постоянная
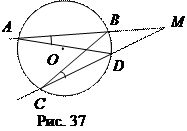


Δ СВМ (Ð А = Ð С – как вписанные углы, опирающиеся на одну и туже дугу ВD, Ð М – общий), то 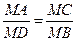


Следствие 1. Произведение секущей, проведённой через точку М, находящуюся на расстоянии а от центра круга
радиуса R, а > R, на её внешнюю часть равна а 2 – R 2 .
Действительно, по теореме 1:
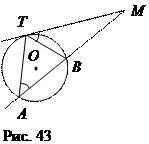
МА 

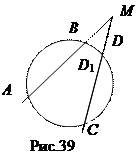


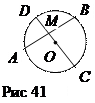
Доказательство. Пусть через точки А, В, С проведена окружность и D1 – её вторая точка пересечения с прямой МС. Тогда по теореме 1: МА 






Доказательство.Пусть через точку М внутри круга с центром О произвольно проведены две хорды АВ и СD. Докажем, что МА 

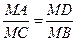


Следствие 2. Произведение частей хорды, на которые она делится точкой М, находящейся на расстоянии а от центра круга радиуса R, а 2 – а 2 .
МА 

Теорема 4. Если отрезки АВ и СD пересекаются в точке М и МА 

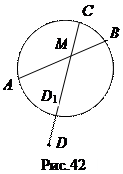






Теорема 5. Произведение секущей, проведённой через точку М вне круга, на её внешнюю часть равно квадрату касательной (рис. 43).
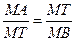


Доказательство.Проведём окружность через точки А, В, С. Пусть С1 – вторая точка пересечения прямой МС с этой окружностью. Тогда по теореме 1 МС 



Задача 1. В круг поместили замкнутую ломанную из пяти звеньев одинаковой длинны. Каждое звено ломаной продолжили до пересечения с окружностью отрезками зелёного и синего цвета, причём из одной вершины ломаной выходят отрезки разного цвета. Доказать, что сумма длин зелёных отрезков совпадает с суммой длин синих.
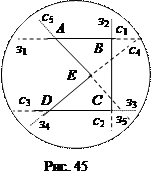
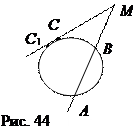
7.2.Из теорем 1 и 3 следует, что величина a 2 – R 2 является характеристикой взаимного расположения круга и точки из плоскости круга, где а – расстояние от точки до центра круга, R – радиус круга. Величину a 2 – R 2 называют степенью точки по отношению к кругу.
Теорема 7. ГМТ, которые имеют одну и ту же степень в отношении двух кругов, есть перпендикуляр к линии их центров.

По следствию 4.3 точка М принадлежит определённому перпендикуляру к прямой ОО1. Пусть N –произвольная точка перпендикуляра к прямой ОО1, который определён условием ОМ 2 – O1M 2 = R 2 – R1 2 .
Последнее равенство означает, что точка N имеет одинаковые степени по отношению к двум кругам. Доказательство остаётся в силе, если, например, R1 = 0.
Следствие 3. ГМТ, степени которых по отношению к заданной точке равны, есть перпендикуляр к прямой, которая проходит через эту точку и центр окружности.
ГМТ, о которых идёт речь в теореме 7 и следствии 3, называются радикальной осью двух кругов и радикальной осью круга и точки соответственно.
Следствие 4. Два концентрических круга не имеют радикальной оси.
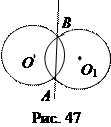
Действительно, степени точек А и В (рис. 47) по отношению к каждому из кругов О и О1 равны нулю.
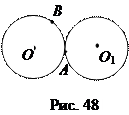
Действительно, если бы радикальная ось имела с окружностью О одну, кроме А, общую точку В (рис. 48), то эта точка должна была иметь степень О и в отношении к кругу О1. Поэтому она принадлежала бы и окружности О1. Но окружности не имеют других общих точек, кроме А. Поэтому радикальная ось является касательной к окружности О, и значит, к кругу О1.
Следствие 7. Радикальные оси любых двух из трёх окружностей или параллельны, или пересекаются в одной точке.
Действительно, если какие-нибудь две из трёх радикальных осей имеют общую точку, то через неё пройдёт и третья радикальная ось.
Видео:Геометрия Из точки А, не лежащей на окружности, проведены к ней касательная и секущая. Расстояние отСкачать

Из точки вне окружности проведена секущая, пересекающая окружность в точках, удаленных от данной на 24 см и 40 см. Расстояние от данной точки
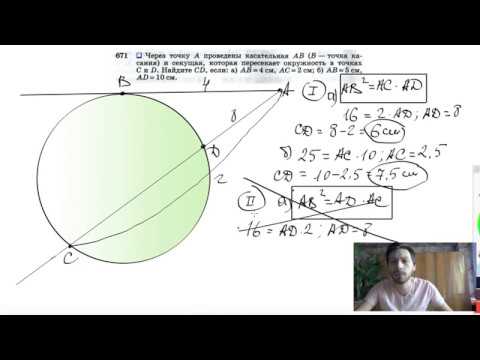
Видео:№671. Через точку А проведены касательная АВ (В — точка касания) и секущая, которая пересекаетСкачать
Ваш ответ
Видео:ОГЭ 2023, сборник Ященко, вариант 18, задача 16Скачать

решение вопроса
Видео:Отрезки касательных из одной точки до точек касания окружности равны | Окружность | ГеометрияСкачать

Похожие вопросы
- Все категории
- экономические 43,282
- гуманитарные 33,619
- юридические 17,900
- школьный раздел 607,049
- разное 16,829
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
🎬 Видео
Всё про углы в окружности. Геометрия | МатематикаСкачать

Теорема о касательной и секущей, проведенных из одной точкиСкачать

8 класс, 32 урок, Касательная к окружностиСкачать

Свойство секущей и касательной, проведённых из одной точки.Скачать

Пойми Этот Урок Геометрии и получай 5-ки — Касательная и ОкружностьСкачать

Секретная теорема из учебника геометрииСкачать

Окружность, касательная, секущая и хорда | МатематикаСкачать

Секущая и касательная. 9 класс.Скачать

Построение касательной к окружности.Скачать

Окружность №16 из ОГЭ. Свойства хорд, касательных, секущих.Скачать

Теорема об отрезках хорд и секущихСкачать

касательная и секущая в окружностиСкачать

теорема о произведении отрезков секущихСкачать

#59. Олимпиадная задача о касательной к окружности!Скачать

9 класс. Геометрия. Теорема о пропорциональности отрезков хорд и в секущих окружности. 22.05.2020.Скачать
