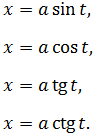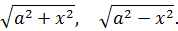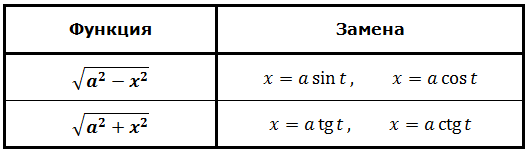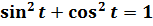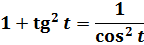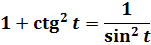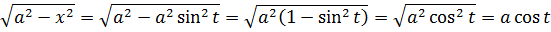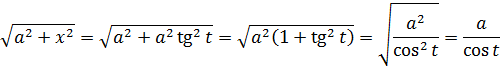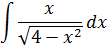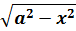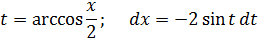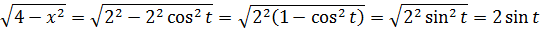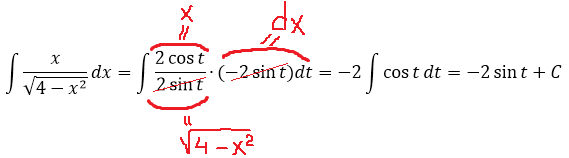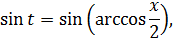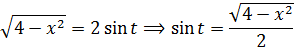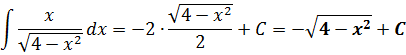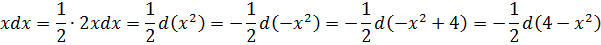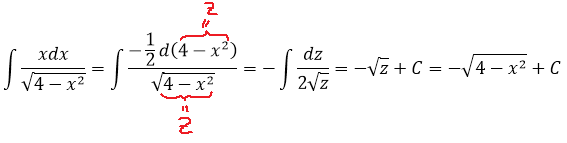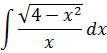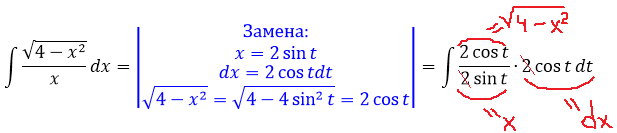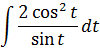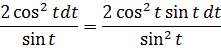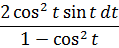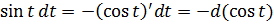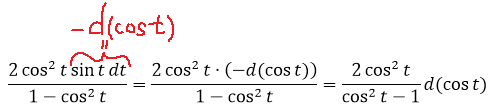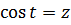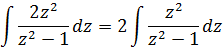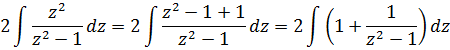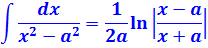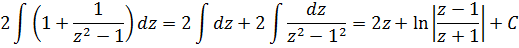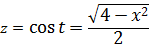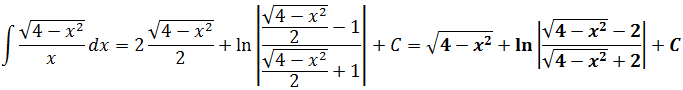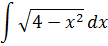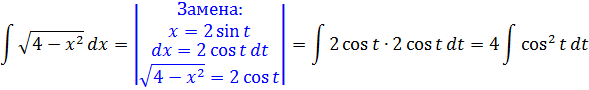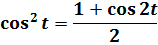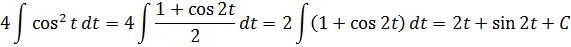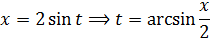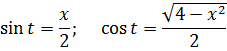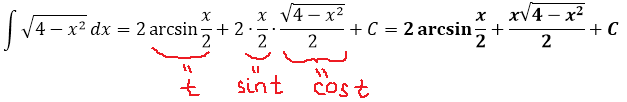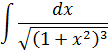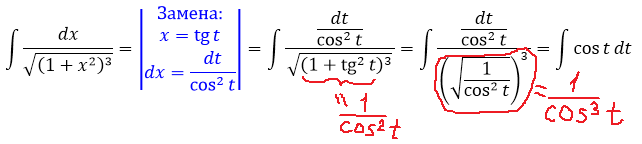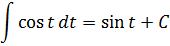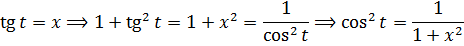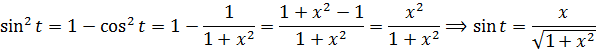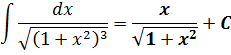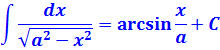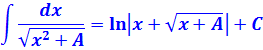Иррациональный тангенс на окружности (3 видео)

Тангенс

Содержание

Тангенс – одна из тригонометрических функций. Как и для всех других функций, значение тангенса определяется для конкретного угла или числа (в этом случае используют числовую окружность.
Аргумент и значение тангенса
Тангенс острого угла
Тангенс можно определить с помощью прямоугольного треугольника — он равен отношению противолежащего катета к прилежащему.
Вычисление тангенса числа или любого угла
Для чисел, а также для тупых, развернутых углов и углов больших (360°) тангенс чаще всего определяют с помощью синуса и косинуса, через их отношение:
Прямая проходящая через начало отсчета на числовой окружности и параллельная оси ординат (синусов) называется осью тангенсов. Направление оси тангенсов и оси синусов совпадает.
Чтобы определить тангенс с помощью числовой окружности, нужно: 1) Отметить соответствующую аргументу тангенса точку на числовой окружности. 2) Провести прямую через эту точку и начало координат и продлить её до оси тангенсов. 3) Найти координату пересечения этой прямой и оси тангенсов.
В отличие от синуса и косинуса значение тангенса не ограничено и лежит в пределах от (-∞) до (+∞), то есть может быть любым.
Знаки по четвертям
Связь с другими тригонометрическими функциями:
Тригонометрическая замена. Интегрируем квадратичные иррациональности!
Значения тангенса и котангенса на тригонометрическом круге
📸 Видео

Тангенс – одна из тригонометрических функций. Как и для всех других функций, значение тангенса определяется для конкретного угла или числа (в этом случае используют числовую окружность.

Видео:10 класс, 11 урок, Числовая окружностьСкачать

Аргумент и значение тангенса

Аргументом тангенса может быть:
— как число или выражение с Пи: (1,3), (frac), (π), (-frac) и т.п.
— так и угол в градусах: (45^°), (360^°),(-800^°), (1^° ) и т.п.

Для обоих случаев тангенс вычисляется одинаковым способом – либо через значения синуса и косинуса, либо через тригонометрический круг (см. ниже).

Видео:Тригонометрическая окружность. Как выучить?Скачать

Тангенс острого угла

Тангенс можно определить с помощью прямоугольного треугольника — он равен отношению противолежащего катета к прилежащему.

1) Пусть дан угол и нужно определить тагенс этого угла.

2) Достроим на этом угле любой прямоугольный треугольник.

3) Измерив, нужные стороны, можем вычислить тангенс.

Видео:Алгебра 10 класс. 2 октября. Тангенс и котангенс на окружностиСкачать

Вычисление тангенса числа или любого угла

Для чисел, а также для тупых, развернутых углов и углов больших (360°) тангенс чаще всего определяют с помощью синуса и косинуса, через их отношение:

Пример. Вычислите (tg:0).
Решение: Чтобы найти тангенс нуля нужно найти сначала синус и косинус (0). И то, и другое найдем с помощью тригонометрического круга :

Точка (0) на числовой окружности совпадает с (1) на оси косинусов, значит (cos:0=1). Если из точки (0) на числовой окружности провести перпендикуляр к оси синусов, то мы попадем в точку (0), значит (sin:⁡0=0). Получается: (tg:0=) (frac) (=) (frac) (=0).

Пример. Вычислите (tg:(-765^circ)).
Решение: (tg: (-765^circ)=) (frac)
Что бы вычислить синус и косинус (-765^°). Отложим (-765^°) на тригонометрическом круге. Для этого надо повернуть в отрицательную сторону на (720^°) , а потом еще на (45^°).

Однако можно определять тангенс и напрямую через тригонометрический круг — для этого надо на нем построить дополнительную ось:

Прямая проходящая через начало отсчета на числовой окружности и параллельная оси ординат (синусов) называется осью тангенсов. Направление оси тангенсов и оси синусов совпадает.

Ось тангенсов – это фактически копия оси синусов, только сдвинутая. Поэтому все числа на ней расставляются так же как на оси синусов.

Чтобы определить тангенс с помощью числовой окружности, нужно:
1) Отметить соответствующую аргументу тангенса точку на числовой окружности.
2) Провести прямую через эту точку и начало координат и продлить её до оси тангенсов.
3) Найти координату пересечения этой прямой и оси тангенсов.

2) Проводим через данную точку и начало координат прямую.

3) В данном случае координату долго искать не придется – она равняется (1).

Пример. Вычислите (tg: 45°) и (tg: (-240°)).
Решение:
Для угла (45°) ((∠KOA)) тангенс будет равен (1), потому что именно в таком значении сторона угла, проходящая через начало координат и точку (A), пересекает ось тангесов. А для угла (-240°) ((∠KOB)) тангенс равен (-sqrt) (приблизительно (-1,73)).

Значения для других часто встречающихся в практике углов смотри в тригонометрической таблице.

В отличие от синуса и косинуса значение тангенса не ограничено и лежит в пределах от (-∞) до (+∞), то есть может быть любым.

При этом тангенс не определен для:
1) всех точек (A) (значение в Пи: …(-) (frac) ,(-) (frac) , (frac) , (frac) , (frac) …; и значение в градусах: …(-630°),(-270°),(90°),(450°),(810°)…)
2) всех точек (B) (значение в Пи: …(-) (frac) ,(-) (frac) ,(-) (frac) , (frac) , (frac) …; и значение в градусах: …(-810°),(-450°),(-90°),(270°)…) .

Так происходит потому, что прямая проходящая через начало координат и любую из этих точек никогда не пересечет ось тангенсов, т.к. будет идти параллельно ей. Поэтому в этих точках тангенс – НЕ СУЩЕСТВУЕТ (для всех остальных значений тангенс может быть найден).

Из-за этого при решении тригонометрических уравнений и неравенств с тангенсом необходимо учитывать ограничения на ОДЗ .

Видео:Синус, косинус, тангенс, котангенс за 5 МИНУТСкачать

Знаки по четвертям

С помощью оси тангенсов легко определить знаки по четвертям тригонометрической окружности. Для этого надо взять любую точку на четверти и определить знак тангенса для нее описанным выше способом. У всей четверти знак будет такой же.

Для примера на рисунке нанесены две зеленые точки в I и III четвертях. Для них значение тангенса положительно (зеленые пунктирные прямые приходят в положительную часть оси), значит и для любой точки из I и III четверти значение тангенса будет положительно (знак плюс).
С двумя фиолетовыми точками в II и IV четвертях – аналогично, но с минусом.

Видео:Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Связь с другими тригонометрическими функциями:

— котангенсом того же угла: формулой (ctg⁡:x=) (frac)
Другие наиболее часто применяемые формулы смотри здесь .

Видео:ТРИГОНОМЕТРИЯ С НУЛЯ - Единичная Окружность // Подготовка к ЕГЭ по МатематикеСкачать

Тригонометрическая замена. Интегрируем квадратичные иррациональности!

Итак, друзья, продолжаем знакомиться с типовыми заменами при вычислении неопределённых интегралов. В прошлый раз мы познакомились с наиболее часто употребляемой степенной заменой, усвоили, как и где именно она применяется, порешали несложные примеры с корнями. Суть степенной замены заключалась в том, что старая переменная интегрирования икс заменялась степенной функцией от новой переменной t. И после такой замены у нас пропадали все корни.

В этом уроке речь пойдёт о так называемой тригонометрической замене. Суть её тоже очень простая и заключается в следующем: старая переменная икс заменяется на некоторую… тригонометрическую функцию от t. Да-да! Всего возможно четыре варианта:

Параметр а — некоторая положительная константа. Зачем она там нужна, станет ясно чуть ниже. На примерах.)

А теперь будем разбираться, где именно применяется такая замена и что она нам даёт. Заодно и элементарную тригонометрию повторим. 🙂

Тригонометрическая замена, так же, как и степенная, применяется при интегрировании некоторых функций с корнями. Только, в отличие от степенной замены, для тригонометрической есть два важных условия её применения:

1) Подынтегральная функция содержит квадратный (и только квадратный!) корень;

2) Под корнем стоит квадратичная конструкция вида a 2 ±x 2 .

Иными словами, в сегодняшнем уроке речь пойдёт о вычислении интегралов, содержащих вот такие корни:

Для плюса и для минуса используется своя замена. Вот вам небольшая сводная табличка:

Выбирать можно любую из предложенных подстановок: для минуса хоть синус, хоть косинус, а для плюса — либо тангенс, либо котангенс. Что больше нравится. 🙂

Суть тригонометрической замены полностью аналогична — убрать корень. То есть, добиться того, чтобы под корнем получился точный квадрат и корень извлекался начисто. И, тем самым, исчез из примера.)

Как же это происходит? Для полного понимания нам понадобится три до боли знакомых школьных тождества:

А теперь возьмём какой-нибудь из корней (пусть первый корень, с минусом в подкоренном выражении) и подставим в него нашу замену (допустим, с синусом a·sin t). Что у нас получится:

Для корня с плюсом проделаем всё то же самое, но на примере подстановки с тангенсом:

Вот и вся суть. Был корень — и нету корня! Возможно, кто-то хмыкнет скептически: какая, мол, разница, корень под интегралом или тригонометрия?! Хрен редьки не слаще… А в чём-то тригонометрия даже и похуже корней будет!

Что ж, настало время удивить скептиков. На примерах.) Итак, начнём!

Пример 1

Подынтегральная функция содержит корень вида

Число а у нас — двойка: 4 = 2 2 . Раз под корнем минус, то используем замену либо с синусом, либо с косинусом. Давайте, с косинусом возьмём. Для разнообразия.)

Итак, замена: x = 2cos t

Сразу же можно выразить само t, а также dx:

А теперь, используя нашу замену, упрощаем сам корень, который нам так мешает:

Вот и отлично. Корня больше нет. Теперь посмотрим, что же у нас получится под интегралом после такой замены:

И как вам? Был интеграл от ужасного корня, а после замены стал табличный (!) интеграл. От косинуса, правда, ну и что в этом страшного? 🙂

Осталось лишь вернуться обратно к переменной икс и записать ответ. Только я не буду сейчас тупо в лоб считать что-то типа

а сразу найду синус t из равенства, где мы упрощали наш корень:

Всё. Подставляем это выражение в наш результат вместо sin t и окончательно получаем:

И все дела.) Да-да, вот такой вот простенький ответ у этого примера.) Можете даже в уме его продифференцировать и получить подынтегральную функцию. 🙂

Особо глазастые студенты при первом взгляде на пример, возможно, узрели вот такую взаимосвязь:

Что ж, респект глазастым! 🙂 Да, действительно, если внести подкоренное выражение 4-х 2 под дифференциал, то пример элементарно сведётся к табличной степенной функции:

Можно так интегрировать? А почему — нет? Математика не запрещает. Но нам ведь размяться с тригонометрической заменой нужно! Вот и изучаем на несложном примере. 🙂

А теперь пример посложнее. Поменяем местами в нашей подынтегральной функции числитель и знаменатель. То есть, просто перевернём подынтегральную функцию. Вот такой пример будем решать:

Пример 2

Давайте, в этот раз используем замену с синусом. Сразу пишем:

И теперь, после подстановки, наш новый интеграл стал выглядеть вот так:

Что делать дальше? Главное — не бояться! И смекалки немного. 🙂

Вообще говоря, на такого рода функции есть свой приём интегрирования (тоже замена, кстати), но мы пока сделаем вид, что про неё не знаем. 🙂 И попробуем выкрутиться с помощью элементарных преобразований, которые мы с вами уже знаем. )

Что здесь можно сделать? Ну, напрашивается подведение под дифференциал, ибо в дроби сидят синус и косинус — родственнички по производной.) Для этого надо попробовать преобразовать подынтегральное выражение так, чтобы везде осталась одна функция — либо синус, либо косинус. Здесь можно всё свести к косинусу. Смотрите, как это делается! По пунктам:

1. Умножаем числитель и знаменатель дроби (вместе с dt!) на sin t. Что именно это даст — узнаем дальше.

2. Заменяем в знаменателе sin 2 t на 1-cos 2 t. Согласно основному тригонометрическому тождеству, ага. 🙂

и подводим косинус под знак дифференциала (про минус тоже не забываем, да).

Вот так. Теперь всё подынтегральное выражение у нас сведено к косинусу. Я согласен, что ещё надо было додуматься домножить всё на sin t, чтобы выйти на такую комбинацию. Но тут уже только богатый опыт рулит. Такое чутьё приходит только с практикой. Так что — решайте примеры! Чем больше, тем лучше.)

Итак, теперь смело заменяем косинус новой буквой. Тэ у нас уже использовано, пусть зэт будет:

Выражаем наш интеграл теперь уже через переменную z:

А теперь в дело вступает наш старый добрый излюбленный приёмчик — отнять/прибавить единичку. 🙂 Продолжаем:

Единичка, я надеюсь, ни у кого проблем в интегрировании не вызывает? А что же касается дроби 1/(z 2 -1), то это не что иное, как табличный интеграл! Открывайте нашу таблицу и ищите похожую формулу. Это седьмая формула, с «высоким» логарифмом:

В роли «а» у нас выступает единичка. Возвращаемся к нашим баранам:

Что ж, заготовка для ответа получена. Теперь поэтапно возвращаемся обратно к иксу:

Вот такой вот интересный пример. И довольно красивый ответ.)

Маньяки могут его продифференцировать. Я продифференцировал. Всё гуд.)

Продолжаем развлекаться. 🙂 Теперь вообще уберём знаменатель и решим вот такой примерчик:

Пример 3

Под интегралом теперь стоит просто чистый корень, безо всего. И тут тоже на помощь придёт тригонометрическая замена.) Давайте, снова будем всё выражать через синус, ибо он удобнее: минус лишний не всплывает, который легко потерять. Действуем:

Как теперь быть с косинусом в квадрате? Если в прошлом примере нам пришлось домножать всё на синус, то тут всё гораздо проще. Призываем на помощь школьную тригонометрию! На сей раз — формулы понижения степени. А чуть конкретнее — вот эту:

И после такого преобразования наш интеграл легко превращается в сумму табличных (ну, или почти табличных :)):

Надеюсь, особо не нужно комментировать, как именно при интегрировании получился синус двух t? Кто не понял — читаем урок « Подведение функции под знак дифференциала ». Там всё популярно изложено. 🙂

Всё. «Рыба» для ответа готова. Осталось правильно перейти к иксу да подставить вместо t в выражения 2t и sin 2t.

Прежде всего, выясним из нашей замены, что же такое это самое t:

Теперь раскроем синус двойного угла: sin2t = 2sin t·cos t

Зачем так сделано? А затем, что теперь и синус и косинус легко выражаются через x (смотрим синюю табличку с нашей заменой)! Вот так:

И теперь наш окончательный ответ полностью готов:

Ну как? Да, я согласен, не самые простые примеры. Так и мы с вами уже всё-таки на приличном уровне, правда?

Что-то мы всё с синусами да косинусами возимся, а тангенс/котангенс как-то обделили вниманием. Давайте и такой примерчик рассмотрим! На десерт.) Он совсем несложный: хватит с вас жести на сегодня! 🙂 Просто чтобы суть замены уловить.)

Пример 4

Не пугаемся внешнего вида примера! Внешность иногда бывает обманчива, да.)

Сразу замечаем под корнем сумму 1+х 2 . Раз сумма, то, стало быть, подходящая замена для ликвидации корня — с тангенсом (или котангенсом). Опять же, по причине нежелания возиться с лишним минусом, я выберу тангенс (а = 1, x = tg t):

И снова перед нами безобидный табличный интеграл! Интегрируем косинус и — готово дело:

Всё. Выражаем теперь нашу первообразную через икс. Как? По формулам тригонометрии, вестимо! У нас есть тангенс, а нас интересует синус.

Так. Квадрат косинуса готов. Осталось лишь из основного тригонометрического тождества вытащить квадрат синуса, извлечь корень и — цель достигнута!

Вот и наш ответ. Довольно простенький на сей раз:

Подытожим наш урок. Давайте разберёмся, зачем в самом начале урока я высказал два обязательных требования, чтобы сам корень был только квадратным (а не кубическим или какой-то более высокой степени), а также чтобы под корнем находилась конструкция вида x 2 ±a 2 . Догадались, почему?

Да потому, что в любой другой ситуации (кубический корень или же под корнем многочлен более высокой степени) у нас просто-напросто не исчезнет иррациональность, и данная замена нам уже никак не поможет свести интеграл к красивому виду. 🙂 И, если вам, вдруг, попался такой пример, то, скорее всего, преобразования более хитрые.

Разумеется, подобные интегралы не ограничиваются этими четырьмя примерами. И для интегралов, содержащих квадратичные иррациональности, есть и более суровые подстановки — Эйлера и Абеля. Но такие подстановки — уже высший пилотаж в интегрировании. Их мы будем изучать ближе к концу раздела. Зато тщательный разбор этих четырёх примеров даст вам возможность уверенно брать хотя бы некоторые интегралы подобного типа. Так что тригонометрическая замена — штука весьма полезная. Мы с ней дружить будем. 🙂 А для дружбы, конечно же, необходимо хорошо знать школьную тригонометрию — основные тождества (их шесть), двойные углы, формулы понижения степени и т.д.

Что ж, на сегодня хватит. А в качестве тренировочного упражнения в этот раз я дам небольшое творческое задание. Чтобы скучно не было.)

Есть в нашей замечательной табличке интегралов парочка довольно страшных формул. Вот эти:

И теперь, в качестве задания, я предлагаю вам доказать эти формулы! С помощью тригонометрической замены, да.) Чтобы вы прочувствовали, откуда что в математике берётся. И берётся явно не с потолка.)

С первой формулой проблем возникнуть не должно: там всё очевидно. А вот со второй («длинным логарифмом») я немного подскажу. В формуле число А для определённости предполагается положительным. Раз оно положительное, то можно совершенно спокойно заменить это самое А на a 2 . И дальше работать уже с заменой через тангенс.) Материала этого (и прошлых) уроков вполне достаточно, чтобы одолеть это задание. Будет вам там парочка сюрпризов! Выручат свойства логарифмов и первообразных (это подсказка! :)).

Видео:Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Значения тангенса и котангенса на тригонометрическом круге

В прошлой статье мы познакомились с тригонометрическим кругом и научились находить значения синуса и косинуса основных углов.

Как же быть с тангенсом и котангенсом ? Об этом и поговорим сегодня.

Где же на тригонометрическом круге оси тангенсов и котангенсов?

Ось тангенсов параллельна оси синусов (имеет тоже направление, что ось синусов) и проходит через точку (1; 0).

Ось котангенсов параллельна оси косинусов (имеет тоже направление, что ось косинусов) и проходит через точку (0; 1).

На каждой из осей располагается вот такая цепочка основных значений тангенса и котангенса: Почему так?

Я думаю, вы легко сообразите и сами. 🙂 Можно по-разному рассуждать. Можете, например, использовать тот факт, что и

Собственно, картинка за себя сама говорит.

Если не очень все же понятно, разберем примеры:

Пример 1.

Вычислить

Находим на круге . Эту точку соединяем с точкой (0;0) лучом (начало – точка (0;0)) и смотрим, где этот луч пересекает ось тангенсов. Видим, что

Ответ:

Пример 2.

Вычислить

Находим на круге . Точку (0;0) соединяем с указанной точкой лучом. И видим, что луч никогда не пересечет ось тангенсов.

не существует.

Ответ: не существует

Пример 3.

Вычислить

Находим на круге точку (это та же точка, что и ) и от нее по часовой стрелке (знак минус!) откладываем (). Куда попадаем? Мы окажемся в точке, что на круге у нас (см. рис.) названа как . Эту точку соединяем с точкой (0;0) лучом. Вышли на ось тангенсов в значение .

Так значит,

Ответ:

Пример 4.

Вычислить

Поэтому от точки (именно там будет ) откладываем против часовой стрелки .

Выходим на ось котангенсов, получаем, что

Ответ:

Пример 5.

Вычислить

Находим на круге . Эту точку соединяем с точкой (0; 0). Выходим на ось котангенсов. Видим, что

Ответ:

Теперь, умея находить по тригонометрическому кругу значения тригонометрических функций (а я надеюсь, что статья, где мы начинали знакомство с кругом и учились вычислять значения синусов и косинусов, вами прочитана…), вы можете пройт и тест по теме «Нахождение значений косинуса, синуса, тангенса и котангенса различных углов».