Интересные факты о подобных треугольниках (5 видео)

Подобные треугольники.

Презентация создана с целью расширения знаний о применении подобия треугольников при решении задач. Была использована на уроке и оказала существенную помощь учащимся при изучении данной темы. В работе рассмотрены три признака подобия треугольников, приведены примеры решения задач, есть задачи и для самостоятельного решения. А также приведены интересные факты из истории.

Содержание

Скачать:
Подписи к слайдам:
Математика, которая мне нравится
Как подобные треугольники помогли спасти невиновного
Работа моих учеников. Презентация «Исторические факты о подобии треугольников» (8 класс)
Описание презентации по отдельным слайдам:
🔍 Видео

Видео:Подобные треугольникиСкачать

Скачать:

Вложение	Размер
prezentatsiya_glazova1.pptx	2.37 МБ

Предварительный просмотр:

Видео:Подобие треугольников. Вся тема за 9 минут | ОГЭ по математике | Молодой РепетиторСкачать

Подписи к слайдам:

Презентация на тему: «Подобные треугольники» Ф.И.О.: Глазова Я.А. Ученица 8 «А» класса МОУ СОШ №1 E-mail : yana.yana.glazova.glazova@mail.ru Ф.И.О. преподавателя: Егорова Н.В. Можайск 2016 год

Подобие в жизни

Животные Архитектурные здания Транспорт Игрушки Техника

Учение о подобии фигур было создано в Древней Греции в V—IV вв. до н. э. трудами Гиппократа Хиосского , Архита Тарентского , Евдокса Книдского и др. Оно изложено в VI книге «Начал» Евклида. Уже в 16 веке нужды землемерия, строительства и военного дела привели к созданию рукописных руководств геометрического держания. Жители Древнего Египта задались вопросом: «Как найти высоту одной из громадных пирамид?» Фалес нашёл решение этой задачи. Он воткнул длинную палку вертикально в землю и сказал: «Когда тень от этой палки будет той же длины, что и сама палка, тень от пирамиды будет иметь ту же длину, что и высота пирамиды.» Немного об истории

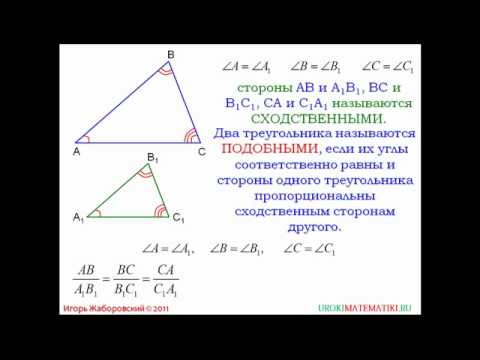
Определение подобных треугольников Два треугольника называются подобными , если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого. Что же такое ТРЕУГОЛЬНИК? Треугольник – простейший многоугольник, имеющий 3 вершины (угла) и 3 стороны; часть плоскости, ограниченная тремя точками и тремя отрезками, попарно соединяющими эти точки.

Признаки подобия треугольников Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны. Если , , то

Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны. Если , , то

Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны. Если , то

После того, как мы ознакомились с признаками подобия треугольников, нам нужно потренироваться использовать наши приобретенные знания на практике. Для этого рассмотрим задачи

Задача №1. Через точки М и N, принадлежащие сторонам АВ и ВС треугольника ABC соответственно, проведена прямая МN, параллельная стороне АС. Найдите длину СN, если ВС = 6, МN = 4 и АС = 9 . Решение: 1) у них – общий 2 ) , как соответственные углы при пересечении параллельных прямых MN и AC секущей AB Из подобия треугольников вытекает пропорциональность соответствующих сторон: . Обозначим NC за x . Соответственно, BN = 6 – x согласно условию. Тогда ; ; Ответ : по I признаку http://school-collection.edu.ru/

Задача №2. Человек ростом 1,9 метра стоит на некотором расстоянии от столба, на котором висит фонарь. Высота фонарного столба 5,7 метра. А человек отбрасывает тень длиной в 5 шагов. На расстоянии скольких метров от человека расположен фонарный столб? Решение: по I признаку , http://school-collection.edu.ru / 1) у них – общий 2) соответственные углы при пересечении параллельных прямых MN и AC секущей AB. Из подобия треугольников вытекает пропорциональность соответствующих сторон: AC = AN + CN, CN = AC – AN = 15 – 5 = 10( м) Значит, человек стоит на расстоянии 10 метров от столба. Ответ: 10м

Задачи для самостоятельной работы. №1. Здание высотой 15 метров Гулливер закрыл монетой диаметром 2 см, держа ее на расстоянии 70 см от глаза. На каком расстоянии от здания находится Гулливер? Ответ: 525м №2. В треугольнике ABC точка N принадлежит BC , точка M принадлежит AC. BC = 18 см, CM = 9 см, CN = 6см, AC = 12 см. Докажите, что треугольники ABC и MNC подобны.

Вывод Данная презентация наглядно представила информацию по теме «Подобные треугольники», была использована на уроке, оказала существенную помощь при изучении темы. Мы убедились, что подобие окружает нас в жизни. Зная признаки подобия треугольников, можно определить высоту какого-либо предмета или рассчитать расстояние до недоступной точки. Таким образом, признаки подобия треугольников – одно из важнейших понятий геометрии. Оно широко используется не только в научных целях, но и в жизни.

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Математика, которая мне нравится

Математика для школьников и студентов, обучение и образование

Видео:Как ПОНЯТЬ ГЕОМЕТРИЮ за 5 минут — Подобие ТреугольниковСкачать

Как подобные треугольники помогли спасти невиновного

Может быть, вы уже читали здесь о том, как знание математики спасло жизнь физику Игорю Евгеньевичу Тамму. А сегодня история, произошедшая совсем недавно, о том, как подобные треугольники помогли невиновному человеку избежать тюрьмы.

Как-то в студенческую канцелярию университета Вандербильта (Теннеси, США) позвонил адвокат, ему ответил студент Курт Кент. Как будто какой-то мужчина выхватил у женщины кошелек, а после этого быстро прошел мимо внешней камеры наблюдения. Это было, когда уже стемнело, и камера не запечатлела его лицо, однако на земле была четко видна тень этого человека, которую он отбрасывал, так как его освещал единственный источник света на торце здания. Кроме того, на земле имелись отметки, позволяющие точно сказать, где стоял человек и где оканчивалась его тень. Адвокат спросил Курта, можно ли сказать, какого роста был человек, запечатленный на видео. Курт ответил, что он может это сделать, потому что это простая задача о подобных треугольниках, которую все изучают.

Курт вместе с адвокатами пошел на то место, где была снята пленка и сделал некоторые измерения. После этого, используя два различных кадра видео, он определил, что рост человека на пленке составлял 6’1” или 6’2” (6 футов 1 дюйм 185 см или 6 футов 2 дюйма 188 см). Адвокат попросил Курта, чтобы кто-нибудь проверил его выкладки. Это сделали двое преподавателей, которые подтвердили его правоту. Однако пойманный поблизости бездомный, которого арестовали за данное преступление, был ростом всего 5’7” ( 170 см). Курт выступил в качестве свидетеля (как свидетель эксперт, не меньше) на в некотором роде предварительных слушаниях, в результате чего адвокат разбил обвинения против бездомного, основываясь на заключении Курта.

Вот таким образом подобные треугольники спасли невиновного человека от тюрьмы.

Видео:ПОДОБНЫЕ ТРЕУГОЛЬНИКИ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

Работа моих учеников. Презентация «Исторические факты о подобии треугольников» (8 класс)

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Работа ученика 8 «б» класса МБОУ СОШ № 50 г. Новосибирска Грецких Константина

Уже в XVI в. нужды землемерия, строительства и военного дела привели к созданию рукописных руководств геометрического содержания. Первое дошедшее до нас сочинение этого рода носит название «О земном верстании, как землю верстать». Оно является частью «Книги сошного письма», написанной, как полагают, при Иване IV в 1556 г. Сохранившаяся копия относится к 1629 г. При разборе Оружейной Палаты в Москве в 1775 г. была обнаружена инструкция «Устав ратных, пушечных и других дел, касающихся до военной науки», изданная в 1607 и 1621 годах и содержащая некоторые геометрические сведения, которые сводятся к определенным приемам решения задач на нахождение расстояний.

Для измерения расстояния от точки Я до точки Б (см. рис.) рекомендуется вбить в точке Я жезл примерно в рост человека. К верхнему концу жезла Ц прилагается вершина прямого угла угольника так, чтобы один из катетов (или его продолжение) проходил через точку Б. Отмечается точка З пересечения другого катета (или его продолжения) с землей. Тогда расстояние БЯ относится к длине жезла ЦЯ так, как длина жезла к расстоянию ЯЗ. Для удобства расчетов и измерений жезл был разделен на 1000 равных частей. Немного из истории Вот один пример из «Устава ратных, пушечных и других дел, касающихся до военной науки»:

За шесть веков до нашей эры греческий мудрец Фалес Милетский вычислил высоту египетской пирамиды, измерив длину её тени. Как это было, рассказывается в книге Я.И.Перельмана «Занимательная геометрия». Фалес, говорит предание, избрал день и час, когда длина собственной его тени равнялась его росту. В этот момент высота пирамиды должна также равняться длине отбрасываемой его тени. Вот, пожалуй, единственный случай, когда человек извлёк пользу из своей тени. ПРИТЧА:

« Усталый чужеземец пришёл в страну Великого Хапи. Солнце уже садилось, когда он подошёл к великолепному дворцу фараона. Он что-то сказал слугам. По мановению руки распахнулись перед ним двери и провели его в приёмную залу. И вот он стоит в запылённом походном плаще, а перед ним на золоченом троне сидит фараон. Рядом стоят высокомерные жрецы, хранители великих тайн природы. — Кто ты? – спросил верховный жрец. — Зовут меня Фалес. Родом я из Милета. Жрец надменно продолжал: — Так это ты похвалялся, что сможешь измерить высоту пирамиды, не взбираясь на неё? – Жрецы согнулись от хохота. — Будет хорошо, — насмешливо продолжал жрец, — если ты ошибёшься не более чем на 100 локтей. — Я могу измерить высоту пирамиды и ошибусь не более чем на пол-локтя. Я сделаю это завтра. Лица жрецов потемнели. Какая наглость! Этот чужеземец утверждает, что может вычислить то, чего не могут они – жрецы великого Египта. — Хорошо, — сказал фараон. – Около дворца стоит пирамида, мы знаем её высоту. Завтра проверим твоё искусство».

На следующий день Фалес нашёл длинную палку, воткнул её в землю чуть поодаль пирамиды. Дождался определённого момента. Провёл некоторые измерения, сказал способ определения высоты пирамиды и назвал её высоту.

Когда тень от палки будет той же длины, что и сама палка, то длина тени от центра основания пирамиды до её вершины будет иметь ту же длину, что и сама пирамида. СЕ=ED, т.е. H=b Преимущества: не требуются вычисления. Недостатки: нельзя измерить высоту предмета при отсутствии солнца и, как следствие, тени.

«Таинственный остров» (фр. L’Île mystérieuse) — роман-робинзонада французского писателя впервые опубликованный в 1874 году. Является продолжением известных произведений Верна «20000 лье под водой» и «Дети капитана Гранта». В книге повествуется о событиях, происходящих на вымышленном острове, где остановился капитан Немо на своей подводной лодке «Наутилус». Основными персонажами являются пятеро американцев, которые оказываются на необитаемом острове в Южном полушарии.

Нахождения четвертого неизвестного члена пропорции. Преимущества: можно производить измерения в любую погоду; простота формулы. Недостатки: нельзя измерить высоту предмета не испачкавшись, так как приходится ложиться на землю.

 АВD подобен EFD (по двум углам):  ВАD= FED=90°; АDВ = EDF, т.к. угол падения равен углу отражения. В подобных треугольниках сходственные стороны пропорциональны: ; . ; . ; .

Преимущества: можно производить измерения в любую погоду; одежда будет чистой; простота формулы; Недостатки: нужно специальное приспособление: зеркало.

По построению  АВС подобен  А1В1С1 (по двум углам). В подобных треугольниках сходственные стороны пропорциональны: А В С А1 В1 С1

Нахождение ширины озера Длина тени земного шара