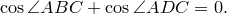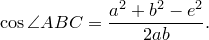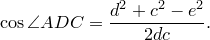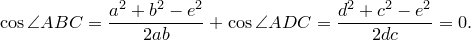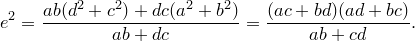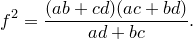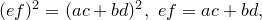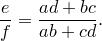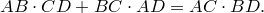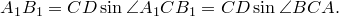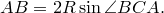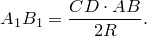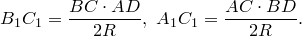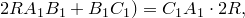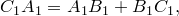Характеристические свойства окружности проект

Видео:Геометрия 8 класс (Урок№28 - Свойства хорд окружности.)Скачать

Презентация по теме: «Свойства окружности»

Работа содержит свойства окружности.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Скачать:

Предварительный просмотр:

Видео:Свойство диаметра окружности. 7 класс.Скачать

Подписи к слайдам:

Презентация по теме: «Свойства окружности» Работу выполнила Ходырева Алина, ученица 9 «В» класса, тел. : 326-89-30 Южное окружное управление городского комитета образования ГОУ СОШ № 941, Бирюлево – Восточное ул. Лебедянская , д. 14, корп. 3 Тел. 329-86-94, sch941@sinergi.ru.rosoft Руководитель: Учитель математики: Малеева Елена Владимировна, тел. : 328-70-04 Руководитель учреждения: Мухина Татьяна Викторовна г. Москва 2011 г.

Что же такое окружность? Рассмотрим два определения окружности: ‘(1) Окружность’ — геометрическое место точек плоскости , равноудалённых от заданной точки, называемой центром, на заданное ненулевое расстояние , называемое её радиусом . ‘(2) Окружность’ — Геометрическая фигура на плоскости, образованная множеством точек, равноудалённых от данной (её центра). Окружность и её центр

Основные термины Касательная Прямая, имеющая с окружностью только одну общую точку , называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности. ( рис. 1 ) Хорда Отрезок, соединяющий две точки окружности, называется ее хордой. Хорда, проходящая через центр окружности, называется диаметром. ( рис. 2 ) Рис. 1 Рис. 2

2. Отрезки касательных к окружности, проведенных из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности. (рис. 4) Свойства касательной 1. Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания. (рис. 3) Рис. 3 Рис. 4

Свойства хорд 1. Диаметр (радиус), перпендикулярный к хорде, делит эту хорду и обе стягиваемые ею дуги пополам. Верна и обратная теорема: если диаметр (радиус) делит пополам хорду, то он перпендикулярен этой хорде. ( рис. 5) 2. Дуги, заключенные между параллельными хордами, равны. (рис. 6) Рис. 6 Рис. 5 3. Если две хорды окружности, AB и CD пересекаются в точке M, то произведение отрезков одной хорды равно произведению отрезков другой хорды: AM•MB = CM•MD. ( рис. 7) Рис. 7

Свойства окружности Прямая может не иметь с окружностью общих точек; иметь с окружностью одну общую точку ( касательная ); иметь с ней две общие точки (секущая). Через три точки, не лежащие на одной прямой, можно провести окружность, и притом только одну. Точка касания двух окружностей лежит на линии, соединяющей их центры .

Теорема о касательной и секущей Если из точки, лежащей вне окружности, проведены касательная и секущая , то квадрат длины касательной равен произведению секущей на ее внешнюю часть: MC 2 = MA•MB.

Теорема о секущих Если из точки, лежащей вне окружности, проведены две секущие , то произведение одной секущей на её внешнюю часть равно произведению другой секущей на её внешнюю часть. MA•MB = MC•MD.

Углы в окружности Центральным углом в окружности называется плоский угол с вершиной в ее центре. Угол, вершина которого лежит на окружности, а стороны пересекают эту окружность, называется вписанным углом. Любые две точки окружности делят ее на две части. Каждая из этих частей называется дугой окружности. Мерой дуги может служить мера соответствующего ей центрального угла. Дуга называется полуокружностью, если отрезок, соединяющий её концы, является диаметром.

Свойства углов, связанных с окружностью 1. Вписанный угол либо равен половине соответствующего ему центрального угла, либо дополняет половину этого угла до 180°. (Рис. 9 и 10) Рис. 9 и 10 2. Углы, вписанные в одну окружность и опирающиеся на одну и ту же дугу, равны. (Рис. 11) Рис. 11

3. Вписанный угол, опирающийся на диаметр , равен 90° (Рис. 10) 4. Угол, образованный касательной к окружности и секущей , проведенной через точку касания, равен половине дуги, заключенной между его сторонами . ( Рис. 11) Рис. 10 Рис. 11

Длины и площади 1. Длина окружности C радиуса R вычисляется по формуле: C = 2 π R . 2. Площадь S круга радиуса R вычисляется по формуле: S = π R 2 . 3. Длина дуги окружности L радиуса R с центральным углом ,измеренным в радианах, вычисляется о формуле: L = α R . 4. Площадь S сектора радиуса R с центральным углом в альфа радиан вычисляется по формуле: S = ½ R 2 α .

Вписанные и описанные окружности Окружность и треугольник: центр вписанной окружности — точка пересечения биссектрис треугольника , ее радиус r вычисляется по формуле: r = S/p где S — площадь треугольника, а p = ( a+b+c ) /2 — полупериметр;

центр описанной окружности — точка пересечения серединных перпендикуляров , ее радиус R вычисляется по формуле: R = 1/2 a/ sin альфа; R = abc / 4S здесь a , b , c — стороны треугольника, альфа — угол, лежащий против стороны a , S — площадь треугольника; центр описанной около прямоугольного треугольника окружности лежит на середине гипотенузы ; центр описанной и вписанной окружностей треугольника совпадают только в том случае, когда этот треугольник — правильный .

Окружность и четырехугольники около выпуклого четырехугольника можно описать окружность тогда и только тогда, когда сумма его внутренних противоположных углов равна 180°: α + γ = β + φ = 180 °;

в четырехугольник можно вписать окружность тогда и только тогда, когда у него равны суммы противоположных сторон: a + c = b + d ;

около параллелограмма можно описать окружность тогда и только тогда, когда он является прямоугольником ; около трапеции можно описать окружность тогда и только тогда, когда эта трапеция — равнобедренная ; центр окружности лежит на пересечении оси симметрии трапеции с серединным перпендикуляром к боковой стороне; в параллелограмм можно вписать окружность тогда и только тогда, когда он является ромбом .

Видео:Основные свойства окружности. Формулы связанные с окружностьюСкачать

Разные виды окружностей и теоремы, с ними связанные.

Окружностью называется геометрическая фигура, состоящая из всех точек плоскости,расположенных на заданном расстоянии от данной точки

Вписанная и описанная окружность, формулы для вычисления радиусов, площадей.

Окружность Аполлония — геометрическое место точек плоскости, отношение расстояний от которых до двух заданных точек — величина постоянная, не равная единице.

Биполярные координаты — ортогональная система координат на плоскости, основанная на кругах Аполлония.

Пусть на плоскости даны две точки A и B. Рассмотрим все точки P этой плоскости, для каждой из которых

где k — фиксированное положительное число. При k = 1 эти точки заполняют срединный перпендикуляр к отрезку AB; в остальных случаях указанное геометрическое место — окружность, называемая окружностью Аполлония.

Просмотр содержимого документа
«Разные виды окружностей и теоремы, с ними связанные.»

“А в окружность я влюбился и на ней остановился.”

Цель проекта: Изучить свойства, виды разных окружностей и теоремы, с ними связанные.

Я начал свою работу с того , что изучил свойства окружности в школьном курсе геометрии по учебнику А.В.Погорелова “Геометрия 7-9” и материал за рамками школьного курса. При сборе информации из различных источников и в работе над проектом я расширил свои знания и буду продолжать дальше изучать эту тему и делиться знаниями с одноклассниками и всеми , кому это интересно.

Окружность — геометрическое место точек плоскости, равноудалённых от заданной точки, называемой центром, на заданное ненулевое расстояние, называемое её радиусом. Замкнутый круг, не имеющий внутренное пространство.

Окружность диаметра AB — это фигура, состоящая из точек A, B и всех точек плоскости, из которых отрезок AB виден под прямым углом.

Окружность — это фигура, состоящая из всех точек плоскости, для каждой из которых отношение расстояний до двух данных точек равно данному числу, отличному от единицы. (см. Окружность Аполлония)

Также фигура, состоящая из всех таких точек, для каждой из которых сумма квадратов расстояний до двух данных точек равна заданной величине, большей половины квадрата расстояния между данными точками.

Радиус — не только величина расстояния, но и отрезок, соединяющий центр окружности с одной из её точек.

Отрезок, соединяющий две точки окружности, называется её хордой. Хорда, проходящая через центр окружности, называется диаметром.

Окружность называется единичной, если ее радиус равен единице. Единичная окружность является одним из основных объектов тригонометрии.

Любые две несовпадающие точки окружности делят её на две части. Каждая из этих частей называется дугой окружности. Дуга называется полуокружностью, если отрезок, соединяющий её концы, является диаметром.

Клавдий Птолемей (), живший в конце первого — начале второго века н.э., был древнегреческим ученым-астрономом, математиком, астрологом, географом, оптиком и теоретиком музыки. Он известен как комментатор Евклида. Птолемей пытался доказать знаменитый Пятый постулат. Основной труд Птолемея — “Альмагест”, в котором он изложил сведения по астрономии. Включал “Альмагест” и каталог звездного неба.

Теорема Птолемея. Вокруг четырехугольника можно описать окружность тогда и только тогда, когда произведение его диагоналей равно сумме произведений его противоположных сторон.

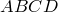
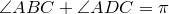
Доказательство необходимости. Поскольку четырехугольник вписан в окружность, то

, откуда

Из треугольника 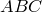по теореме косинусов находим

Аналогично из треугольника :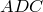

Сумма этих косинусов равна нулю:

Отсюда выразим :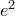

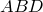
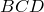
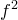
Рассмотрим треугольники и и найдем :

что и требовалось доказать.

Попутно мы доказали еще одно утверждение. Для четырехугольника, вписанного в окружность,

Доказательство достаточности. Пусть выполнено равенство

Докажем, что вокруг четырехугольника 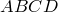можно описать окружность.

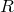
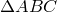
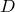
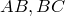
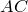
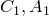
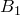
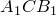
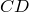
Обозначим через радиус окружности, описанной вокруг . Из точки опустим перпендикуляры на прямые и и обозначим точки пересечения этих прямых и перпендикуляров к ним через и соответственно. По теореме синсов для треугольника получаем (диаметр описанной окружности для этого треугольника равен ):

По теореме синусов для треугольника 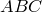имеем

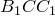
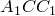
Таким же образом, рассматривая треугольники и получим соотношения

Отсюда, подставляя эти выражения в исходное равенство, имеем

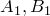
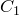
откуда следует, что точки и лежат на одной прямой.

Докажем теперь, что из этого следует, что вокруг четырехугольника 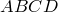можно описать окружность (достаточное условие теоремы Симсона).

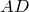
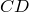
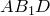
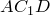
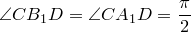
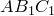
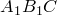
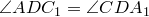
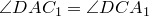
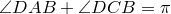
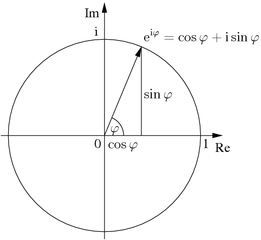
Построим окружности на отрезках и как на диаметрах. Первая из них проходит через точки и (углы и прямые), а вторая — через точки и (). Углы и равны как вертикальные, откуда следует, что , а значит, и . Отсюда , и вокруг четырехугольника можно описать окружность.

Формула Эйлера названа в честь Леонарда Эйлера, который её ввёл, и связывает комплексную экспоненту с тригонометрическими функциями.

Формула Эйлера утверждает, что для любого вещественного числа x выполнено следующее равенство:

,

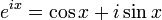
где e — основание натурального логарифма,

i — мнимая единица.

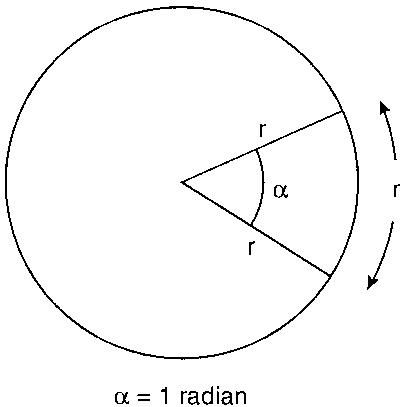
Угол, образуемый дугой окружности, равной по длине радиусу, принимается за 1 радиан.

Длина единичной полуокружности обозначается через π.

Видео:Окружность. 7 класс.Скачать

Методический материал по теме «Свойства окружности»

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

«Календарь счастливой жизни:
инструменты и механизм работы
для достижения своих целей»

Сертификат и скидка на обучение каждому участнику

Свойства касательных к окружности

Окружность, вписанная в произвольный треугольник

Окружность, вписанная в трапецию и описанная около трапеции.

Формула отрезка общей касательной к двум касающимся окружностям

В школьном курсе геометрии уделяется немного уроков для изучения темы «Окружность», учащиеся узнают о взаимном расположении окружностей и многоугольников и окружности, получают формулы для нахождения радиуса окружности, вписанной в правильный треугольник, квадрат и правильный шестиугольник, а также формы для радиусов описанных окружностей около квадрата, правильного треугольника и шестиугольника. Но остается открытым вопрос о том, как же находить радиус окружности, вписанной в произвольный треугольник, как связаны отрезки касательных к окружности с радиусом и углами треугольника.

Из школьного курса геометрии известно, где лежит центр окружности, описанной около треугольника, квадрата, правильного шестиугольника, но ведь в окружность можно вписать и трапецию, где в этом случае будет лежать центр этой окружности? Всякую ли трапеции можно вписать в окружность? На эти вопросы поможет ответить данная проектная работа, в которой изложены теоремы и их доказательства, относящиеся к нахождению элементов окружности и многоугольников, как вписанных в окружность, так и описанных около нее. Полученные формулы помогут при решении задач, упростят нахождение радиуса окружности, элементов многоугольника. К тому же в задании ЕГЭ С4 нередко встречаются задачи с вписанными и описанными окружностями. Приведенные факты и формулы помогут сориентироваться учащимся при решении задач на доказательство и нахождение элементов многоугольника из С4.

Окружности, элементы окружностей и многоугольники, вписанные в окружность и описанные около окружности.

— расширить и систематизировать знания об окружностях и многоугольниках, вписанных в окружность и описанных около окружности.

— изучить и обобщить свойства касательной и секущей к окружности;

— вывести: формулы для отрезков касательных к окружности, вписанной в треугольник; формулы радиуса окружности, вписанной в произвольный треугольник; формулу отрезка общей касательной к двум касающимся окружностям;

— изучить особенности окружности, вписанной в трапецию и описанной около нее.

Свойства касательной к окружности

В этом разделе общаются и систематизируются сведения о касательной и секущей к окружности. Приводится доказательство дополнительных свойств, о которых не упоминается в учебнике геометрии, но они могут быть полезны при решении олимпиадных задач и подготовки к экзамену.

Напомним определение касательной и секущей.

Прямая, имеющая с окружностью только одну общую точку, называется касательной к окружности , а их общая точка называется точкой касания прямой и окружности. Секущей называется прямая, пересекающая окружность.

Основные свойства касательной к окружности

Данные свойства и их доказательства приводят в учебнике геометрии.

Отрезки касательных к окружности, проведенные из одной точки, равны.

На рисунке изображены две касательные к окружности. AB и AC – отрезки касательных к окружности. AB = AC .

Углы, образованные касательными, проведенными из одной точки, и прямой, проходящей через центр окружности и эту точку, равны.

На рисунке выше, прямая AO является биссектрисой , значит,

Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.

На рисунке касательная проведена к окружности в точке A , тогда прямая

Здесь приведем доказательства свойств касательной и секущей к окружности, которые могут быть полезны для вычисления углов и отрезков касательных.

Если из точки, лежащей вне окружности, проведены касательная и секущая, то квадрат длины касательной равен произведению секущей на ее внешнюю часть.

На рисунке МС – касательная, MA – секущая, тогда MC 2 = MA·MB.

Если из точки к окружности проведены касательная и секущая, то квадрат отрезка касательной от данной точки до точки касания равен произведению длин отрезков секущей от данной точки до точек её пересечения с окружностью.

На рисунке МА – касательная, МВ – секущая, тогда МА 2 =МВ·МС

Доказательство: , и следовательно,. У АМС и ВМА угол при вершине М общий, то эти треугольники подобны по двум углам (первый признак подобия треугольников). Из подобия следует: , значит, МА 2 =МВ·МС.

Угол между касательными и хордой. Величина угла, образованного касательной и хордой, имеющими общую точку на окружности, равна половине угловой величины дуги, заключенной между его сторонами.

∠ NAB — угол между касательной MN и хордой AB , имеющих на окружности общую точку A , тогда ∠ NAB== (180 о — ∠ BOC) = ∠ АОВ или ∠ NAB = .

Доказательство: Дополнительное построение. Проводим диаметр АС. Касательная перпендикулярна радиусу, проведенному в точку касания, а, значит, перпендикулярна диаметру АС, тогда ∠ CAN=90 о . – вписанный угол, тогда = , ∠ NAB=90 о -, получаем ∠ NAB== (180 о — ∠ BOC) = ∠ АОВ или ∠ NAB = .

Угол между секущими.

Если точка пересечения двух секущих к окружности находится внутри окружности, то угол между секущими равен половине суммы градусных мер дуг, которые они стягивают.

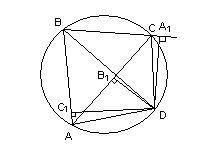
Доказательство: Дополнительное построение. Проведем хорду FR , треугольника FMR получим: Получаем

Если точка пересечения двух секущих к окружности находится вне окружности, то угол между секущими равен половине разности градусных мер дуг, которые они стягивают.

M

Доказательство: Дополнительное построение. Проведем хорду ED , тогда

так как они являются вписанными углами. Из треугольника MED : углами, значит, тогда

Окружность, вписанная в произвольный треугольник

Для выведения формул отрезков касательных к окружности и радиуса окружности, вписанной в треугольник напомним определение окружности, вписанной в треугольник.

Окружность вписана в треугольник, если она касается всех его сторон. Тогда сам треугольник будет описанным вокруг окружности. Расстояние от центра вписанной окружности до каждой из сторон треугольника равно радиусу этой окружности.

Формулы для отрезков касательных к окружности, вписанной в треугольник

Пусть точки K , M , N – точки касания окружности со сторонами треугольника. Стороны треугольника, описанного около окружности лежат на касательных к этой окружности, тогда отрезки касательных равны, то есть AK = AN , BK = BM , CN = CM . Обозначим их соответственно буквами x, y, z .

р – полупериметр треугольника ABC . .

Если окружность вписана в треугольник, то отрезки касательных можно вычислить как разность полупериметра и стороны треугольника, на которой данный отрезок касательной не лежит.

В треугольнике со сторонами a , b , c расстояние от вершины А до точек касания вписанной окружности сторон , содержащих эту вершину , равно , расстояние от вершины B до точек касания вписанной окружности сторон , содержащих эту вершину , равно , расстояние от вершины C до точек касания вписанной окружности сторон , содержащих эту вершину , равно .

Выведем еще одну формулу для вычисления отрезков касательных:

Для доказательства рассмотрим АО N –прямоугольный т.к ONAC (радиус перпендикулярен касательной). AO – отрезок биссектрисы ∠ А => ∠ ONA =

ctg ∠ OAN = , тогда

Окружность, вписанная в трапецию и описанная около трапеции.

Из школьного курса геометрии известно, что в окружность можно вписать любой треугольник, квадрат, правильный шестиугольник. Определим, можно ли в окружность вписать трапецию.

Теорема.

Трапеция вписана в некоторую окружность тогда и только тогда, когда она является равнобедренной.

Доказательство: так как они являются односторонними углами. По теореме Птолемея, е сли у четырёхугольника суммы величин его противоположных углов равны 180°, то около этого

четырёхугольника можно описать окружность, тогда , значит то есть трапеция должна быть равнобедренной.

Следующая теорема показывает, как можно вычислить радиус окружности, вписанной в трапецию.

Если в трапецию вписана окружность с радиусом r и она делит боковую сторону точкой касания на два отрезка — a и b , то B C

Доказательство: Если концы боковой стороны соединит с центром окружности, то образуется прямоугольный треугольник ABO , с прямым углом O . Радиус — это высота, опущенная из его прямого угла в точку касания окружности. Из подобия треугольников BOM и AOM , следует что , тогда .

Центр окружности, описанной около трапеции , лежит на пересечении серединных перпендикуляров к сторонам трапеции.

B C

Доказательство: Проведем диагональ AC , она делит трапецию на два треугольника, вписанных в окружность, значит отрезки AO , BO , CO равны, так как треугольник ABC является вписанным в окружность. Из школьного курса планиметрии известно, что центром описанной около треугольника окружности является точка пересечения серединных перпендикуляров к сторонам треугольника ABC . Но стороны треугольника ABC являются сторонами трапеции ABCD , значит центр окружности, описанной около трапеции, является точкой пересечения серединных перпендикуляров к сторонам трапеции.

Формула отрезка общей касательной к двум касающимся окружностям

Две окружности имеют различное взаимное расположение относительно друг друга, а именно: окружности могут касаться друг друга, пересекаться, не пересекаться, одна окружность может лежать внутри другой. Рассмотрим случай, когда окружности касаются внешним образом. Они имеют общую точку касания.

Рассмотрим понятие внешней касательной к окружности. Прямую называют внешней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по одну сторону от этой прямой. На рисунке прямая a – внешняя касательная к двум касающимся окружностям.

Отрезок общей внешней касательной к двум касающимся окружностям равен ,где R и r –радиусы окружностей.

Пусть AB – общая касательная к окружностям; O 1 и O 2 -центры окружностей , тогда

O ₁ A AB и O ₂ B AB так как радиус, проведенный в точку касания, перпендикулярен касательной. O ₁ ABO ₂ -прямоугольная трапеция. Проведем высоту O ₁ Н.

O ₁ H = AB , O ₂ H = O ₂ B — HB = O ₂ B — O ₁ A = R — r

По теореме Пифагора O ₁ O ₂ = O ₂ H + O ₁ H

Решив квадратное уравнение, получаем:

Данная формула применяется для вычисления отрезка общей касательной к двум касающимся окружностям через радиусы этих окружностей. Задачи, в которых присутствует окружность и касательная часто встречаются в С4 ЕГЭ. Применяя эту формулу мы упростим вычисления при решении подобных задач.

В ходе работы были изучены основные свойства касательной к окружности, доказаны дополнительные свойства, о которых не упоминается в школьном курсе планиметрии. Произведена систематизация этих свойств. Также были выведены формулы для отрезков касательных к окружности, вписанной в треугольник; формулы радиуса окружности, вписанной в произвольный треугольник; формула отрезка общей касательной к двум касающимся окружностям. Были изучены особенности окружности вписанной и описанной в трапеции. Выведена формула для вычисления радиуса вписанной в трапецию окружности.

Полученные знания станут существенным подспорьем в понимании свойств касательной и секущей к окружности. Будут необходимы при решении как задач курса планиметрии, так и олимпиадных и экзаменационных задач.

Учебник по геометрии 7-9 класс, атанасян Л.С. и др.-18-е изд. — М. : «Просвещение», 2008.

Геометрия в 7-9 классах. Березина Л. Ю. и др.- 2-е изд., перераб. И доп. – М. : «Экзамен»,2008

http://eek.diary.ru/ сайт по оказанию помощи абитуриентам, студентам,

учителям по математике.

Полонский В.Б., Рабинович Е.М., Якир М.С. Учимся решать задачи по геометрии. Учеб.-метод. пособие. – К. «Магистр», 1996.

🌟 Видео

Окружность вписанная в треугольник и описанная около треугольника.Скачать

Свойства хорд окружностиСкачать

Окружность №16 из ОГЭ. Свойства хорд, касательных, секущих.Скачать

Вписанная и описанная окружность - от bezbotvyСкачать

Углы, вписанные в окружность. 9 класс.Скачать

Взаимное расположение окружности и прямой. 7 класс.Скачать

✓ Всё, что нужно знать про окружность | ЕГЭ. Задания 1 и 16. Профильный уровень | Борис ТрушинСкачать

Четырехугольники, вписанные в окружность. 9 класс.Скачать

Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Окружность и ее свойства (bezbotvy)Скачать

Математика это не ИсламСкачать

Длина окружности. Площадь круга. 6 класс.Скачать

7 класс, 21 урок, ОкружностьСкачать

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать