График окружности в wolfram mathematica (2 видео)

WolframAlpha по-русски

Математика с WolframAlpha ® . Объяснения с примерами.

Содержание

Окружность в Wolfram|Alpha
Как в mathematica wolfram построить график
Иллюстрированный самоучитель по Mathematica 3/4
WolframAlpha по-русски
Как построить график функции в Wolfram|Alpha
Оцифровка и аппроксимация графиков функций при помощи Wolfram Mathematica и Graph Digitizer
1. Подготовка изображения
2. Оцифровка координат
2.1. Установка системы координат (СК)
2.3. Оцифровка кривой
2.4. Экспорт данных
3. Построение математической модели кривой
🎦 Видео

Окружность в Wolfram|Alpha

Как получить изображение окружности в Wolfram|Alpha? Как с помощью в Wolfram|Alpha построить окружность, если задано ее уравнение, если заданы координаты центра и радиус, если известны три точки, через которые проходит окружность? Как найти координаты точек пересечения окружности и прямой? Такие элементарные задачи Wolfram|Alpha решает легко.

Изображение окружности и основные сведения о ней Wolfram|Alpha выводит по запросу circle:

Если требуется просто крупное изображение окружности и ничего более, используйте запрос circle image:

Как построить окружность с заданными параметрами при помощи Wolfram|Alpha? Это можно сделать несколькими способами.

Во-первых, Wolfram|Alpha, естественно, сможет построить окружность по ее уравнению. Если нужно, можно будет найти, например, координаты центра окружности и ее радиус:

Чтобы построить окружность, если известны координаты центра и радиус, нужно использовать запрос вида circle center (3,4) radius 5, или его упрощенный вариант:

Пример: построить изображение единичной окружности с центром в начале координат.

Через три точки, не лежащие на одной прямой, можно провести единственную окружность. Чтобы построить окружность, проходящую через три точки, не лежащие на одной прямой, Wolfram|Alpha использует другой запрос. При этом система выводит не только изображение, но также уравнение окружности и ее основные параметры — координаты центра окружности (center), радиус (radius), диаметр (diameter), площадь (area), периметр (perimeter):

Чтобы не только найти координаты центра окружности, но и обозначить центр на рисунке, используйте тот же запрос с параметром center:

Еще один способ построить окружность — задать координаты центра и одну точку, через которую проходит эта окружность:

Вместе с окружностью в Wolfram|Alpha можно построить изображение другой линии. Например:

В заключение о том, как в Wolfram|Alpha найти точки пересечения прямой и окружности.

Обычно, чтобы найти координаты точек пересечения прямой и окружности решают систему уравнений прямой и окружности при помощи запроса solve. Этот способ удобен, когда известны уравнения прямой и окружности. Например,

Если же окружность и прямая заданы другим способом, то с помощью Wolfram|Alpha можно найти точки их пересечения, используя запрос intersection:

Наконец, вот еще один пример использования запроса intersection. На этот раз получим пересечение окружности и треугольника

Видео:How to Draw Cone With RevolutionPlot3D in MathematicaСкачать

Как в mathematica wolfram построить график

Видео:Видео курс Wolfram Mathematica | Функция Plot | Часть 1/2Скачать

Иллюстрированный самоучитель по Mathematica 3/4

Графика, как важнейшее средство визуализации вычислений, всегда была козырной картой системы Mathematica и во многом способствовала ее высокой репутации как мирового лидера среди систем компьютерной математики. Обширные графические возможности достигаются при небольшом числе встроенных функций графики за счет их модификации с помощью опций и директив. Благодаря этому Mathematica позволяет строить практически любые виды графиков. Для просмотра и изменения опций графика можно (выделив ячейку с графиком) воспользоваться описанным ранее инспектором опций, в котором есть соответствующий раздел. Однако в этом уроке мы инспектором опций пользоваться не будем – все необходимые опции будут вводиться в соответствующие функции так, как это принято делать при программировании задач графики.

Концептуально графики в системе Mathematica являются графическими объектами, которые создаются (возвращаются) соответствующими графическими функциями. Их немного, около десятка, и они охватывают построение практически всех типов математических графиков. Как уже отмечалось, достигается это за счет применения опций и директив.

Поскольку графики являются объектами, то они могут быть значениями переменных. Поэтому Mathematica допускает следующие конструкции:

Plot[Sin[x],] – построение графика синусоиды;
g: = Plot [Sin [x], ] – задание объекта – графика синусоиды – с отложенным выводом;
g=Plot [Sin [x], ] – задание объекта – графика синусоиды – с немедленным выводом.

Начнем рассмотрение графических возможностей системы с построения простейших графиков функций одной переменной вида у =f(x) или просто f(x). График таких функций строится на плоскости, то есть в двумерном пространстве. При этом используется прямоугольная (декартова) система координат. График представляет собой геометрическое положение точек (х, у) при изменении независимой переменной (абсциссы) в заданных пределах, например от минимального значения xmin до максимального хтах с шагом dx. По умолчанию строятся и линии координатной системы.

Для построения двумерных графиков функций вида f(x) используется встроенная в ядро функция Plot:

Plot [f, ] – возвращает объект, представляющий собой график функции f аргумента х в интервале от xmin до xmax;
Plot[, ] – возвращает объект в виде графиков ряда функций fi.

Функция Plot используется для построения одной или нескольких линий, дающих графическое представление для указанных функций f, f1, f2 и т. д. На рис. 8.1 показано построение графика функции sin(x)/x без использования каких-либо опций (точнее, с набором опций по умолчанию).

Рис. 8.1. Построение двумерного графика

Тут виден как раз тот случай, когда масштаб графика по вертикали выбран системой неудачно – часть графика сверху просто отсекается. В большинстве же случаев применение функции Plot позволяет получить вполне «удобоваримый» график.

Видео:Математика это не ИсламСкачать

WolframAlpha по-русски

Математика с WolframAlpha ® . Объяснения с примерами.

Как построить график функции в Wolfram|Alpha

Начнем с построения простого 2-мерного графика: plot sin(sqrt(7)x)+19cos(x) для x от -20 до 20

Если заменить 7 на (-7), то получим графики действительной и мнимой частей функции: plot sin(sqrt(-7)x)+19cos(x) для x от -5 до 5

В двух предыдущих примерах мы задавали область значений аргумента х. А что будет, если не задавать область значений х?

Одной из уникальных особенностей Wolfram | Alpha является автоматический выбор подходящего диапазона х для построения графиков функций одной и двух переменных, например, как при построении графика этой функции, содержащей функции Бесселя:

Обращаясь к Wolfram | Alpha, чтобы построить график функции, мы всегда используем префикс plot. Если же мы введем какое-либо одномерное выражение без префикса plot, то получим кроме графика функции в прямоугольных декартовых координатах, еще и много других сведений об этой функции.

Кроме того, изображение построенного графика будет крупнее, если вы используете префикс plot.

Одновременно в Wolfram | Alpha можно строить графики нескольких функций.

Если навести мышь на левый нижний угол изображения, то становятся доступными две ссылки: Save as image и Copyable planetext. Рассмотрим такой график:

Первая ссылка Save as image, которая открывается в левом нижнем углу изображения, позволяет сохранить построенный график, как картинку на компьютере пользователя — при нажатии на Save as image автоматически начнется загрузка изображения:

Вторая ссылка Copyable planetext позволяет увидеть код, аналогичный тому, который используется системой Matematica для построения графиков:

Теперь рассмотрим, как в Wolfram | Alpha построить графики функций двух переменных. Начнем с функции y^2 cos(x) для x от -6 до 6 и y от -2 до 2

Все трехмерные графики строятся с помощью функции plot3d системы Mathematica. Контурные графики были сделаны с помощью ContourPlot. В обоих случаях, чтобы увидеть код системы Mathematica для генерации изображения нужно нажать ссылку Copyable planetext в левом нижнем углу нужного изображения.

Видео:Make your PLOTS LOOK PROFESSIONAL (Wolfram Language / Mathematica)Скачать

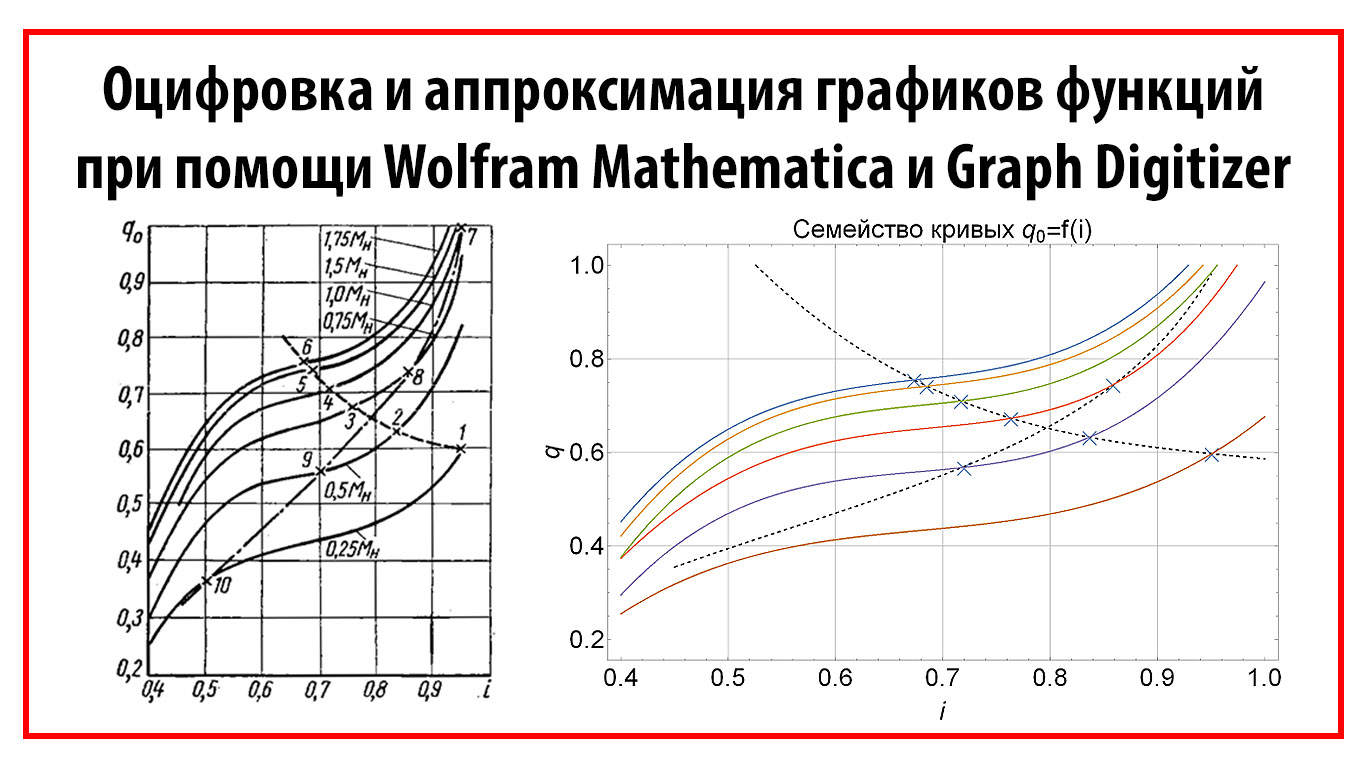
Оцифровка и аппроксимация графиков функций при помощи Wolfram Mathematica и Graph Digitizer

С задачей оцифровки графиков функций и кривых приходится сталкиваться почти каждому инженеру и студенту. Традиционный «ручной» метод очень неудобен и к тому же вносит большие погрешности в данные. Для единоразовой задачи этот метод не так плох, но если графиков больше чем один и на каждом изображена не одна кривая, а семейство кривых?

В процессе выполнения лабораторных практикумов по физике перед мной часто встает задача определить значение функции по её графику представленному на бумаге, для выполнения дальнейших расчётов. Так как обработка подобных графиков на компьютере значительно повышает скорость и точность этого процесса, то было решено изучить возможности для оцифровки графика и построения математической модели кривой, представленной на графике.

В качестве примера, я взял график зависимости КПД генератора от его мощности из лабораторного практикума по электротехнике. Входе выполнения работы мной было выполнено сканирование графика, обработка изображения графика, оцифровка координат и построение математической модели кривой.

1. Подготовка изображения

После сканирования первым делом необходимо привести полученное изображение к полноценному контрасту и выровнять одну из осей графика. Далее необходимо увеличить резкость и изменить размер изображения. При слишком большом размере и разрешении возникают трудности на последующих этапах работы.

Обработку изображений я рекомендую программу Adobe Photoshop. При помощи инструмента Curves добиваемся полноценного контраста, далее при помощи фильтра Smart Sharpen повышаем резкость. Несомненным плюсом Photoshop является возможность обработки большого количества изображений путем записи экшена (Action) и применения его совместно с пакетной обработкой (File – batch processing).

Для большего ускорения процесса обработку можно производить в программе сканирования при помощи заранее заготовленных пресетов или автоматических алгоритмов.

Рисунок 1.1 – Изображение графика До обработки и После обработки

2. Оцифровка координат

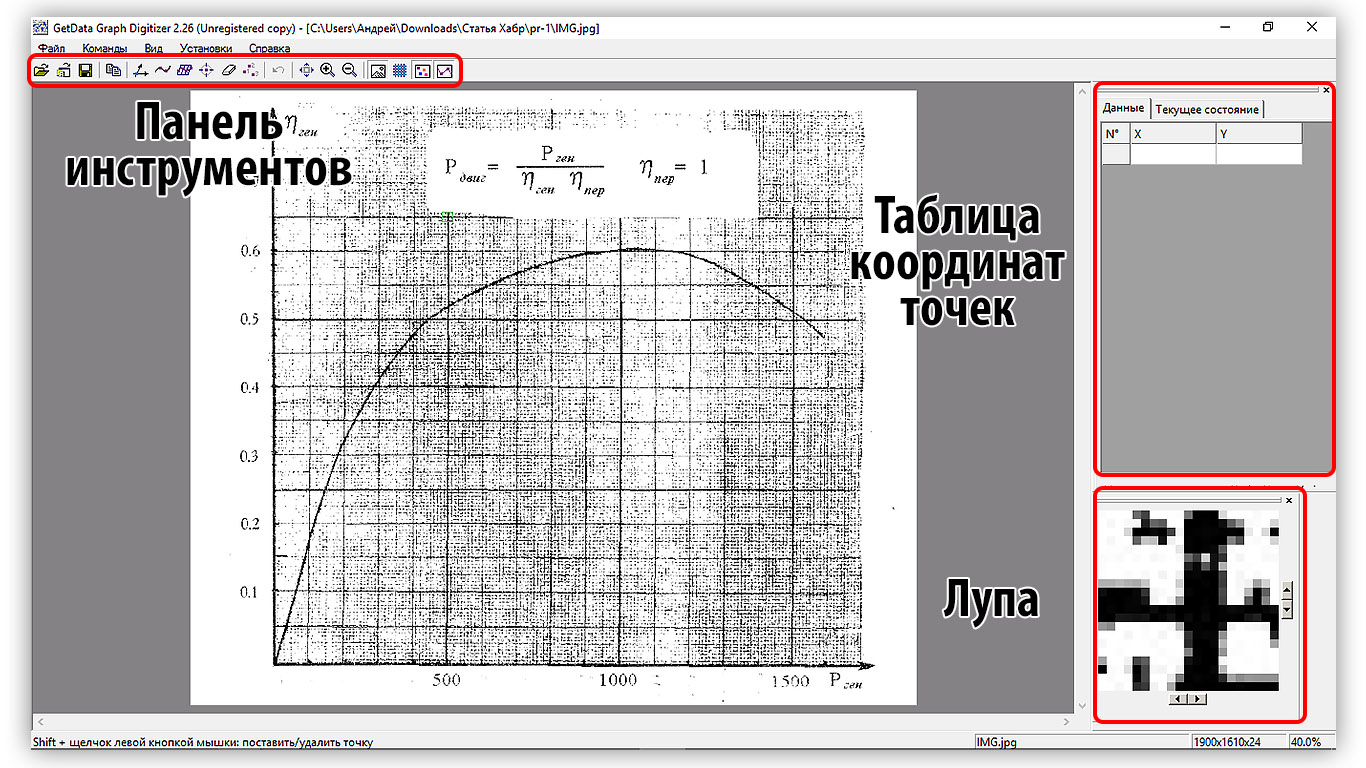
Для оцифровки координат я использовал условно-бесплатную программу GetData Graph Digitize версии 2.26. После запуска программы открываем наше обработанное изображение «Файл – Открыть изображение». После открытия, перед нами предстанет стандартное рабочее пространство.

Рисунок 2.1 – Стандартный интерфейс Graph Digitize

2.1. Установка системы координат (СК)

Первое, что нам необходимо сделать – это установить систему координат, т.е. обозначить линии осей. Для этого переходим «Команды – Установить систему координат». Далее зажав ЛКМ находим точку начала координат и кликаем по ней. В появившемся окне вводим значение начала координат (Xmin). Далее аналогично устанавливаем значения Xmax, Ymin и Ymax. Для удобной установки точек необходимо открыть окошко лупы «Вид — Лупа». После установки опорных точек отобразятся линии осей и откроется окно «Параметры Системы координат» в котором можно переназначить значения опорных точек и установить логарифмический масштаб оси.

Для визуального контроля качества установки СК можно отобразить сетку с заданным шагом «Вид – Показывать сетку». В случае корректной установки СК линии сетки должны быть строго параллельны линиям на изображении графика. Стоит отметить, что при сканировании разворотов график часто оказывается в районе сгиба, и одна из осей получается изогнутой. В данном случае корректно установить СК не представляется возможным, поэтому на этапе сканирования следует плотнее прижимать разворот к стеклу.

Рисунок 2.2 – Вид с установленной системой координат и сеткой

2.3. Оцифровка кривой

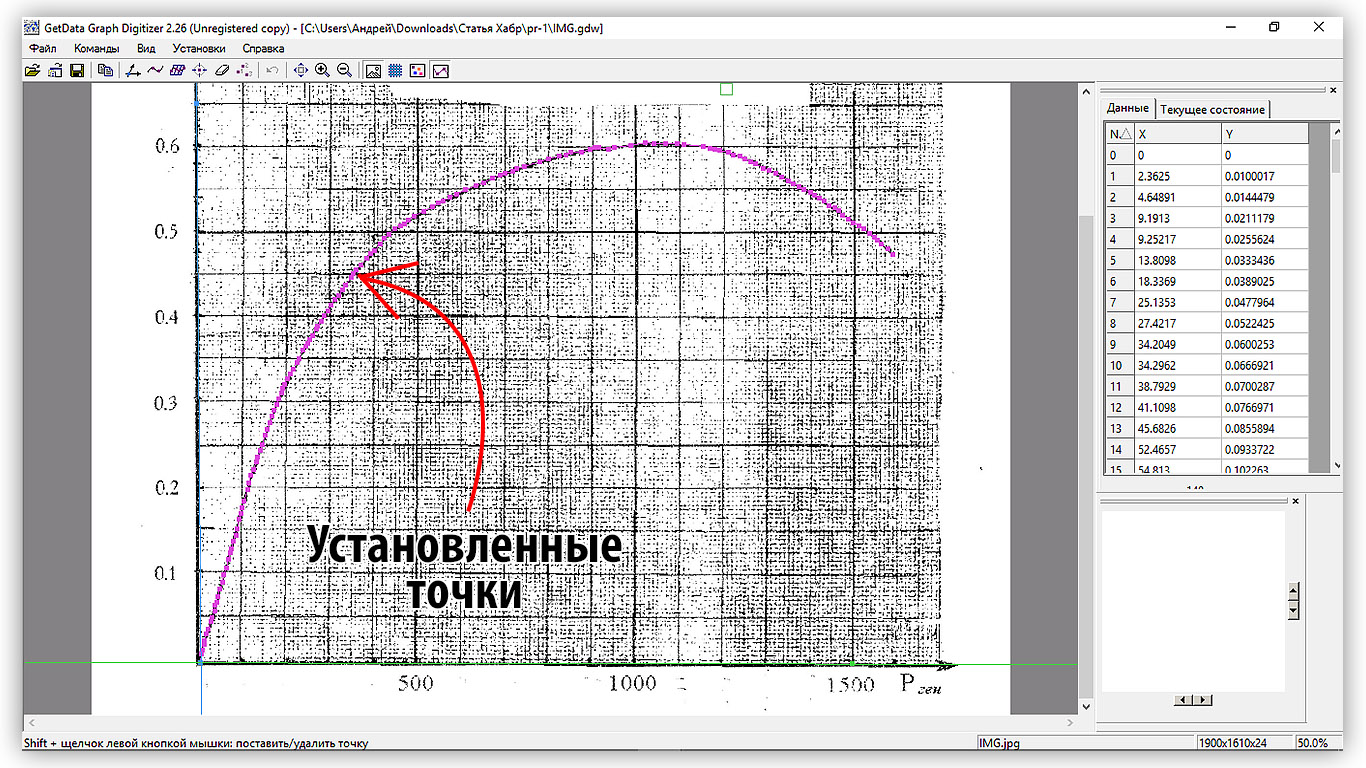
Приступим к установке точек на графике. Для этого перейдем в режим установки точек (Ctrl+P). В данном режиме клик ЛКМ устанавливает новую точку. Для отображения таблицы координат выбранных точек необходимо перейти «Вид – Окно информации». Для удаления точек используется ластик точек данных «Команды — Ластик точек данных» (Ctrl + E)

По моему опыту большее количество точек необходимо устанавливать в окрестности точек перегиба кривой, на линейных участках кривой можно ограничится небольшим их количеством.

Если на графике присутствует больше чем 1 кривая или семейство кривых, то после установки точек на первой нужно добавить новую линию «Команды – Добавить линию». После чего можно будет выставить точки на второй кривой и т.д.

Если на изображении графика нет сетки, то можно воспользоваться автоматическим алгоритмом трассировки кривой (Ctrl + T). При наличии сетки алгоритм выдает много ошибок.

Рисунок 2.3 – Вид с установленными точками на кривой

2.4. Экспорт данных

Для дальнейшей обработки полученных данных необходимо экспортировать координаты точек в .txt файл или в буфер обмена (удобно в случае если у нас только одна кривая). В программе GetData Graph Digitize экспорт в .txt выполняется вызовом команды «Файл – Экспорт данных» (Ctrl + Alt + E). После нажатия в открывшемся окне предлагается задать путь сохранения и имя файла.

Создано программой GetData Graph Digitizer 2.26.0.20, дата создания October 01 2017, 21:16,
на основе файла ‘C:UsersАндрейDownloadsСтатья Хабрpr-1IMG.jpg’

Линия #1
0.00000000000000 0.00000000000000
2.36249828804472 0.0100017499987319
4.64890967470313 0.0144478880812405
9.19129768746544 0.0211179194797685
9.25216720857449 0.0255624090127471
13.8097726016141 0.0333435627945197
18.3369432340991 0.0389024718098030
25.1353078729653 0.0477963965243503
27.4217192596237 0.0522425346068590
34.2048665182127 0.0600253369381616
34.2961707998762 0.0666920712376295
38.7929066718068 0.0700287354864236
41.1097528190197 0.0766971183354215
45.6825755923365 0.0855893945004388
52.4657228509255 0.0933721968317414
54.8130037586929 0.102262824447229
61.5961510172819 0.110045626778531
66.1841911708760 0.120049025326793
70.7417965639155 0.127830179108566
73.0282079505739 0.132276317191075
77.6010307238908 0.141168593356092
84.3689606022025 0.147840273304150
86.7010241296927 0.155619778536392
91.3042816635640 0.166734299467899
95.8466696763263 0.173404330866427
98.1635158235393 0.180072713715425
102.721121216579 0.187853867497197
111.805897242103 0.201193930294253
114.137960769594 0.208973435526496
118.710783542910 0.217865711691513
125.478713421222 0.224537391639571
132.277078060088 0.233431316354119
134.578706827024 0.238988576819872
141.361854085613 0.246771379151175
145.904242098375 0.253441410549703
152.733041497796 0.264557580030739
157.275429510558 0.271227611429267
164.058576769147 0.279010413760570
168.616182162187 0.286791567542342
173.158570174949 0.293461598940870
179.926500053261 0.300133278888928
184.468888066023 0.306803310287456
191.236817944335 0.313474990235514
193.538446711271 0.319032250701268
198.050399963478 0.323480037333306
204.818329841790 0.330151717281364
211.571042339824 0.335712274846178
218.323754837859 0.341272832410991
227.332443961997 0.349057283291824
231.844397214205 0.353505069923862
240.883521098898 0.363511765571184
247.621016216655 0.367961200752753
252.117752088585 0.371297865001547
256.629705340793 0.375745651633586
263.367200458550 0.380195086815154
272.375889582689 0.387979537695987
274.647083589070 0.391314553395251
283.625337952654 0.396876759509595
290.393267830965 0.403548439457653
299.371522194549 0.409110645571996
306.139452072861 0.415782325520054
315.132923816722 0.422455654017642
324.095960800028 0.426906737748741
333.089432543889 0.433580066246329
339.842145041924 0.439140623811142
353.317135277438 0.448039494174280
357.829088529646 0.452487280806318
364.566583647403 0.456936715987887
375.770379876536 0.462500570651760
389.230152731773 0.470288318631653
398.208407095357 0.475850524745997
407.156226698386 0.479190486093851
420.615999553624 0.486978234073743
429.609471297485 0.493651562571331
440.798050146340 0.498104294851960
454.242605621300 0.504780920448608
467.641508955428 0.508124178895523
476.574111178180 0.510353017860132
485.537148161487 0.514804101591231
498.951268875892 0.519258482421390
521.282774432772 0.524830579832913
541.388738124103 0.530401028694907
554.802858838508 0.534855409525066
565.961002926809 0.537085897039205
581.600665506764 0.541541926418894
597.225110706442 0.544886833415338
617.331074397772 0.550457282277332
641.872904439924 0.554919905855141
659.722891505151 0.558266461401115
679.828855196482 0.563836910263109
697.678842261709 0.567183465809083
708.836986350010 0.569413953323222
726.671756034959 0.571649386485952
735.619575637989 0.574989347833806
753.454345322938 0.577224780996536
789.139102073114 0.582806769705239
809.214631003891 0.586154973800744
833.741243665765 0.589506474995308
849.335254104888 0.590629137225263
860.508615573467 0.593970747122647
884.989576094510 0.593988881167477
905.065105025286 0.597337085262982
916.223249113588 0.599567572777121
925.125416575785 0.599574166975241
947.350400470724 0.597368407704052
960.734086424575 0.599600543767722
998.598732899469 0.601850813876222
1032.02751302354 0.605208909268906
1052.04217243321 0.604112623831432
1078.74867481980 0.604132406425792
1105.45517720639 0.604152189020153
1121.01875288496 0.603052606483618
1165.49915543539 0.600863332707730
1181.04751373369 0.598652627787951
1192.16000568116 0.597549748152356
1203.27249762862 0.596446868516762
1223.27193965801 0.594239460696043
1234.35399684493 0.590914336293959
1249.91757252350 0.589814753757425
1260.99962971041 0.586489629355341
1274.30722876288 0.583166153502787
1285.40450333007 0.580952151483948
1303.13275135308 0.575409727963965
1316.45556778582 0.573197374494656
1331.98870870383 0.569875547191632
1345.28109037602 0.565440948955834
1360.79901391376 0.561007999269566
1371.88107110067 0.557682874867482
1385.18867015314 0.554359399014928
1396.27072734005 0.551034274612844
1411.80386825807 0.547712447309821
1420.66038357943 0.544385674358207
1431.74244076635 0.541060549956123
1442.82449795326 0.537735425554039
1453.87612037962 0.532188056385466
1467.19893681236 0.529975702916157
1476.05545213373 0.526648929964543
1484.88153269454 0.521099912246440
1498.17391436673 0.516665314010642
1509.24075417337 0.512229067225314
1522.54835322583 0.508905591372760
1533.63041041275 0.505580466970676
1546.90757470466 0.500034746351633
1557.97441451129 0.495598499566305
1564.60538796711 0.492270078065161
1573.44668590820 0.487832182730302
1588.94939206566 0.482288110660789
1599.98579711174 0.475629619108972

В меню «Установки – Параметры» устанавливается формат вывода данных. Там же можно включить сортировку точек по значению координаты X, если на вашей кривой для каждого X существует уникальный Y, для исключения случайных ошибок в последовательности установке точек.

Рисунок 2.4 – Установки экспорта

3. Построение математической модели кривой

В финале выполним аппроксимацию полученных данных и проверим корректность полученной математической модели. Для этого я предлагаю использовать систему компьютерной алгебры Wolfram Mathematica.

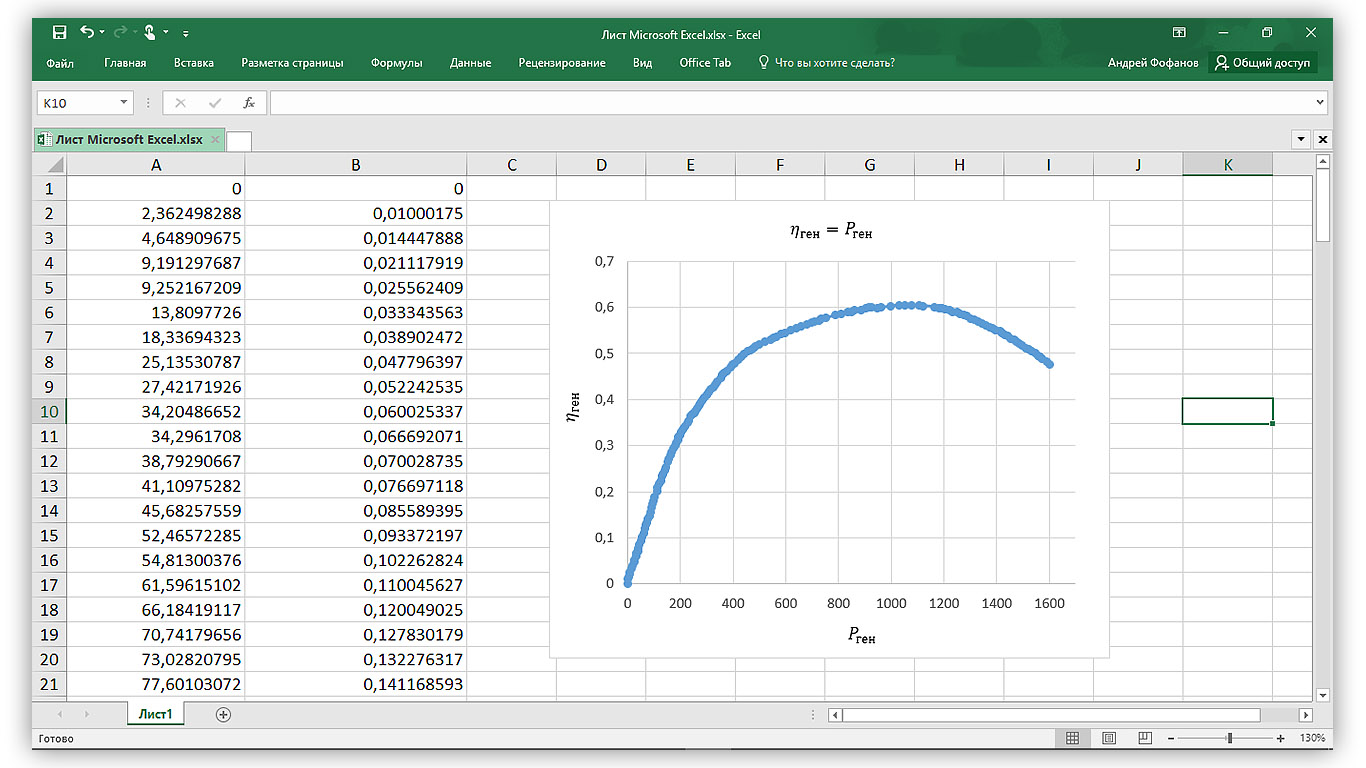
Для быстрого импорта данных в Wolfram Mathematica скопируем координаты точек из экспортированного файла и вставим в пустую ячейку Excel. В итоге на листе появятся 2 колонки данных X и Y соответственно.

Рисунок 3.1 – Данные в Excel

Следующим шагом создаем новый документ Wolfram Mathematica и перетягиваем в него файл Excel. В итоге образуется список списков, содержащий координаты точек. Присвоим ему переменную data.

Рисунок 3.2 – Импортированные данные в Wolfram Mathematica

Отобразим импортированные данные при помощи функции ListPlot[].

Рисунок 3.3 – Графическое отображение точек в виде диаграммы разброса данных

Аппроксимируем точки полиномом 5й степени. Для этого используем функцию LinearModelFit[]. В итоге мы получим объект класса FittedModel[]. Присвоим ему переменную fit.

Вычислим коэффициент детерминации R^2, показывающий какую долю вариации (разброса) переменной, объясняет полученное уравнение. Чем ближе данный коэффициент к единице, тем большую долю вариации объясняет уравнение. Для этого в качестве аргумента функции fit укажем «RSquared». В данном случае R^2 = 0.99, это значит, что наша модель объясняет 99,9% вариации переменной.

Для вычисления значения Y необходимо в качестве аргумента к функции fit указать требуемое значение X.

Рисунок 3.4 – Аппроксимация точек, вычисление коэффициента детерминации и вычисление значения функции

Кроме вычисления коэффициента детерминации, проведем регрессионный анализ. В этот раз в качестве аргумента функции fit укажем «ANOVATable». По полученному результату, можно утверждать, что оправданно использование каждого члена аппроксимирующего полинома. Отобразим полученное уравнение в явном виде, для этого к переменной fit применим функцию Normal[].

Рисунок 3.5 – Регрессионный анализ и полином в явном виде

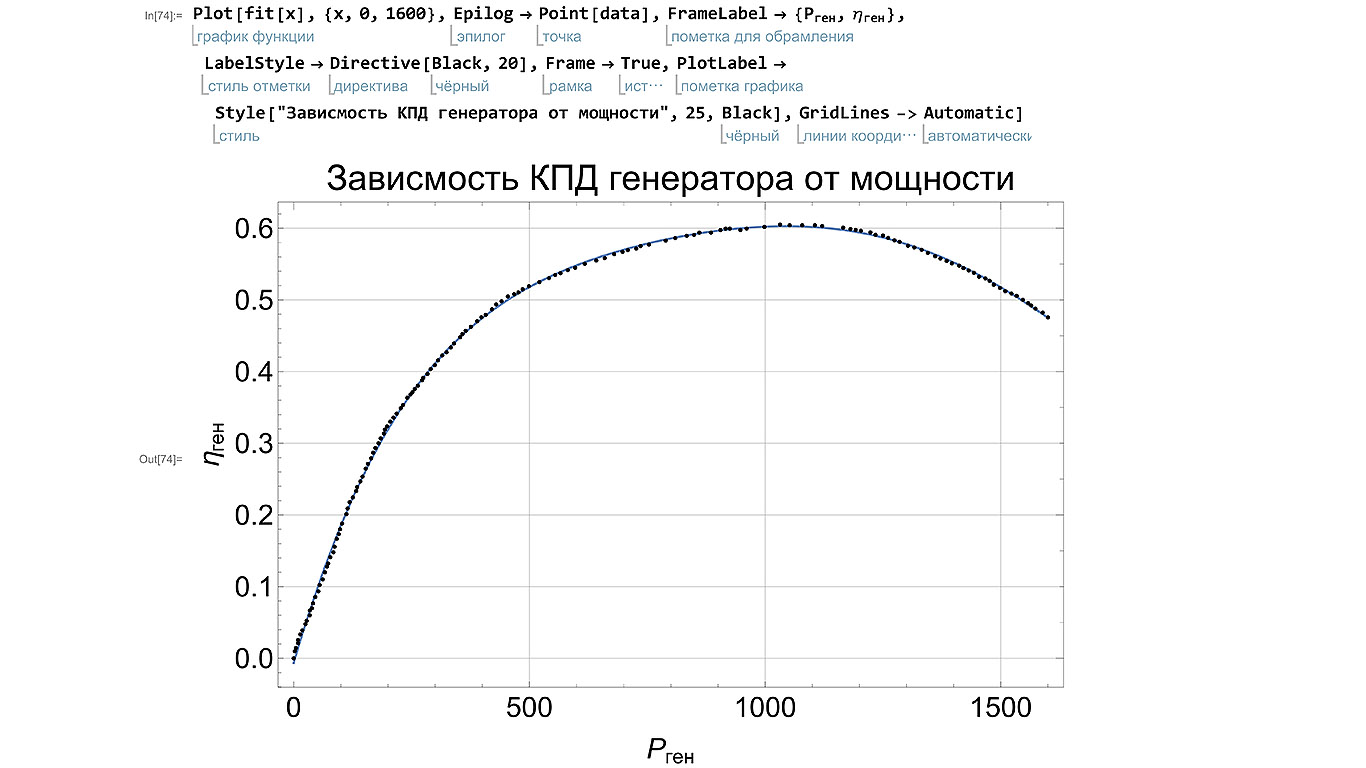
Далее построим график полинома и отобразим на нем исходные точки. При помощи стандартного синтаксиса настроим стиль графика добавим подписи к осям и название графика.

Рисунок 3.6 – Итоговый график

Рисунок 3.7 – Сравнение итогового графика с исходными данными

Возможности для анализа математической модели в Wolfram Mathematica воистину огромны, но мы ограничимся представленными выше. Интересующиеся могут узнать больше путем вычисления функции fit[«Properties»].

В итоге мы изучили возможности применения Wolfram Mathematica и Graph Digitizer для оцифровки графиков и подбора математической модели кривой. Использованное программное обеспечение позволяет выполнить поставленную задачу с минимальными усилиями и с высоким качеством.

Видео:Создание графиков с двумя различными осямиСкачать