Графический треугольник на c

Рисование интерфейсов, формирование таблиц баз данных, работа с сетью — это всё хорошо, но иногда хочется просто, что-нибудь нарисовать, например треугольник . А потом конечно же оживить этот объект, чтобы им можно было управлять, и в последствии превратить этот проект в маленькую игру. Ну кто не хочет написать собственную игру, даже самую простую?

Давайте тогда сделаем первый шаг в сторону простенькой игры, а именно разберемся с рисованием объектов в Qt, попробовав нарисовать треугольник .

Программный код был написан в QtCreator 3.3.1 на основе Qt 5.4.1.

Видео:OpenGL - Урок 2 - точка, линия, треугольник, кругСкачать

Структура проекта «Треугольник»

Опишем структуру проекта, в котором будем рисовать треугольник:

• Triangle.pro — профайл проекта, создается по умолчанию и в данном проекте не требует корректироваки;
• main.cpp — файл, с которого стартует приложение, в данном файле вызывается widget, в котором будет располагаться графическая сцена с треугольником;
• widget.h — заголовочный файл, вызываемого виджета с графической сценой;
• widget.cpp — файл исходных кодов виджета;
• triangle.h — заголовочный файл класса Треугольника , который наследован от QGraphicsItem;
• triangle.cpp — файл исходных кодов класса Треугольник.

1. 1. Структура проекта «Треугольник»
2. 2. mainwindow.ui
3. 3. widget.h
4. 4. widget.cpp
5. 5. triangle.h
6. 6. triangle.cpp
7. 7. Итог
8. 8. Видеоурок

Видео:КАК НАРИСОВАТЬ ТРЕУГОЛЬНИК В КОНСОЛИ C# | C# ДОМАШНИЕ ЗАДАНИЯ | #5Скачать

mainwindow.ui

В дизайнере интерфейсов просто закидываем QGraphicsView в виджет. Больше ничего не требуется.

Видео:Графика с нуля | Растеризация треугольника, интерполяцияСкачать

widget.h

В данном файле всего лишь объявляем графическую сцену и объект треугольника, с которым будем работать.

Видео:Часть 1. Рисуем на C#. Windows Forms. Нажатие мышки. System.Drawing / Класс Graphics.Скачать

widget.cpp

В данном файле настраиваются объекты QGraphicsView , QGraphicsScene, а также создается и устанавливается на графическую сцену объект треугольника.

Видео:КАК НАРИСОВАТЬ ТРЕУГОЛЬНИК В ПРОГРАММЕ ADOBE ILLUSTRATOR.Скачать

triangle.h

А вот теперь настало время проработать сам класс, в котором создаётся треугольник. В данном случае наследуемся от QGraphicsItem .

Видео:Пересечение двух плоскостей. Плоскости в виде треугольникаСкачать

triangle.cpp

А теперь рисуем треугольник в нашем классе. Здесь имеется один важный момент. Координатная система объекта QGraphicsItem — это понятие отличное от координатной системы графической сцены. То есть каждый объект QGraphicsItem или унаследованный от данного класса имеет свою собственную систему координат, которая транслируется в систему координат QGraphicsScene . Когда мы задаём позицию, где будет находиться объект на графической сцене, то мы указываем, где будет находится точка графического объекта, которая имеет координаты 0 по оси X и 0 по оси Y, в координатной системе объекта, поэтому важно, чтобы данная точка была в центре графического объекта. Это упростит дальнейшую работу, если конечно вы осознанно не предполагаете иного варианта.

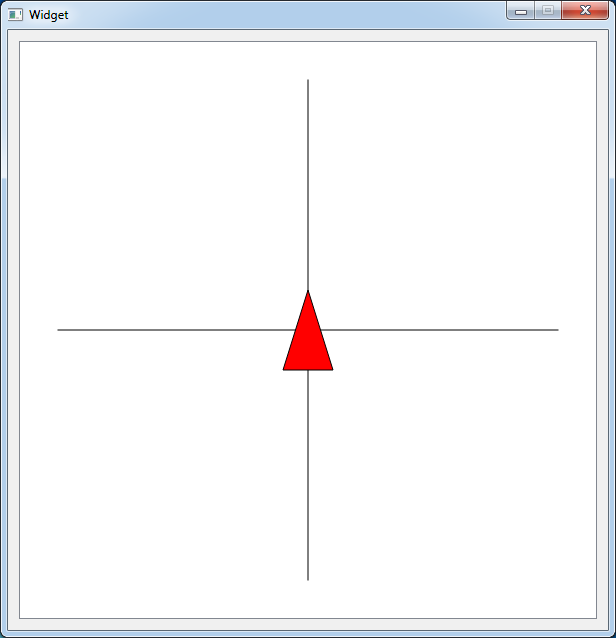
В результате у Вас должно получится приложение, которое выводит на экран красный треугольник в центре графической сцены на пересечении двух линий, как показано на рисунке.

Также рекомендую ознакомиться с видеоуроком, в котором подробнее рассмотрен момент с установкой координат графического объекта.

Видео:Определение натуральной величины треугольника АВС методом замены плоскостей проекцииСкачать

Видеоурок

Рекомендуем хостинг TIMEWEB

Рекомендуемые статьи по этой тематике

Видео:OpenGL #2 - первый треугольникСкачать

2D графика на основе WinApi C++ (2D graphics based on WinApi C++)

Для начала нам потребуется шаблон , на основе которого можно будет создавать дальнейшие приложения. Создайте в Visual Studio пустой проект (File → New → Project→ Other→ Empty). Cоздайте в нем main.cpp файл (Project → Add New Item…) и вставьте туда программный код (см. ниже).

Проследите, чтобы при создании проекта была установка x86 (32-разрядная программа):

32-разрядные программы не могут загружать 64-разрядные библиотеки (DLL-файлы) и могут вылетать, если они попытаются загрузить определенный DLL-файл и обнаружат 64-битную версию вместо 32-разрядной

Если возникают ошибки из-за преобразования символов, то в окне свойств проекта установите «Использовать набор символов Юникода»:

Можете также скачать с моего Google-диска заархивированный файл проекта по ссылке 2d_window.zip. Скачивание начинается после выбора кнопки меню в правом верхнем углу открывшегося окна

Проект создан в версии Visual Studio 17. Для поздних версий (19 и выше), возможно, понадобиться пересобрать решение (кнопки меню Build>Rebuild Solution).

При запуске программы должно появиться окно, залитое синим цветом.

Проект содержит файл main.cpp, ознакомьтесь с программным кодом.

Директива препроцессора #include открывает доступ к тысячам описаний констант, структур, типов данных и функций Windows.

WinAPI приложение является в своей основе процедурным приложением и содержит два основных модуля – функции WinMain и WndProc.

Функция WinMain составляет основу любого WinAPI приложения. Она служит как бы точкой входа в приложение и отвечает за следующее:

• начальную инициализацию приложения;
• создание и регистрацию объекта класса окна приложения;
• создание и инициализацию цикла обработки событий.

Обработанное в бесконечном цикле событие переправляется (опосредовано через Windows) оконной функции WndProc. События в ней идентифицируются именем константы (WM_PAINT, WM_DESTROY и др.). Рисование осуществляется при помощи объектов типа HDC (дескриптор контекста устройства).

Видео:ПОЧЕМУ ГРАФИКА СОСТОИТ из ТРЕУГОЛЬНИКОВ? | РАЗБОРСкачать

Рисуем треугольник в оконной СК

Нарисуем треугольник, задав координаты его вершин в оконной (физической) системе координат. Начало этой системы координат располагается в левом верхнем углу экрана. Ось X направлена слева направо, ось Y – сверху вниз. В качестве единицы длины в этой системе координат используется пиксель.

Для этого создадим заголовочный файл draw.h:

Еще создадим файл draw.cpp:

В файле main.cpp подключим draw.h и закомментируем

А между заполнением области фоновым цветом и выводом изображения на основной контекст, появляется вызов процедуры рисования:

Рисуем мы на контексте-двойнике, а уже потом перекидываем изображение на основной контекст.

Видео:№194. Начертите треугольник. Через каждую вершину этого треугольника с помощью чертежногоСкачать

Логическая система координат

Оконная СК неудобна для пользователя из-за непривычного расположения осей (ось y направлена вниз), задания координат в пикселях и др. Устраним эти недостатки, используя логическую СК, в которой:

• центр координат перенесен из левого верхнего угла в центр экрана;
• направление оси Y меняется на противоположное;
• координаты (от -1 до +1) соотнесены с шириной и высотой окна;
• введен отступ от края окна (margin).

Преобразования из логической системы координат в оконную осуществляются при помощи зависимостей:

X_Window = MARGIN + (1.0/2)*(X_Log + 1)*(Width — 2 * MARGIN);

Y_Window = MARGIN + (-1.0/2)*(Y_Log — 1)*(Height — 2 * MARGIN);

Ниже приводится новый код модуля draw.cpp:

В draw.h добавляется объявление новой функции:

В модуль main.cpp добавляем обработчик события WM_SIZE и WM_ERASEBKGND:

Теперь, при изменении размеров окна наш треугольник подстраивается под новые размеры. При изменении размеров окна происходит перерисовка изображения, поскольку событие WM_SIZE автоматически вызывает событие WM_PAINT.

Контрольные вопросы

1. Чем обусловлен переход от оконной СК к логической?
2. Какие задачи решают функции Tx(0.0), Ty(0.5)?
3. Какие задачи решает функция SetWindowSize?

Видео:Qt Widgets - OpenGL. Создаем окно и рисуем треугольник.Скачать

Поворот плоскости

Алгоритмическая часть

Мы нарисовали треугольник в логической системе координат. Теперь обеспечим возможность поворота треугольника при каждом нажатии клавиш ← или →.

Для пересчета положения каждой вершины треугольника используем преобразование координат при повороте. Рассмотрим произвольный вектор r, задающий некоторую точку в системе координат ху:

При повороте на угол φ координаты точки запишутся в виде:

Выделим из этих уравнений 2 пары зависимостей – для пересчета координат точек в новой СК (1.1) и для обновления значений косинуса и синуса угла (1.2):

В программе поворот реализуется пошагово. На каждом шаге в уравнение 1.1 вместо sin φ и cos φ подставляются sin (α+ φ) и cos (α+ φ), полученные из системы уравнений 1.2. При этом на следующем шаге в уравнении 1.2 вместо cos α и sin α в правую часть уравнения подставляются sin (α+ φ) и cos (α+ φ), которые были получены на предыдущем шаге.

В матричном представлении выражения (1.1) могут быть записаны в одном из следующих видов:

Программная реализация

В программе модифицированы все модули (main.cpp, draw.h, draw.cpp) и добавлены новые (geometry.h, matrix.h, matrix.cpp). В файле main.cpp добавляются обработчики WM_CREATE и WM_KEYPRESSED, клавиши ← и → идентифицируются в программе константами VK_LEFT и VK_RIGHT, начальный поворот плоскости инициализируется вызовом функции InitRotation, текущий поворот – функцией AddRotation. Перерисовка изображения (вызов события WM_PAINT) обеспечивается функцией InvalidateRect.

В файлы draw.h, draw.cpp и main.cpp вносим изменения, которые обеспечивают рисование треугольника в зависимости от текущего значения угла. В определение функций InitRotation и AddRotation входит вызов функции SetRotationMatrix, которая осуществляет инициализацию массива из 4-х тригонометрических характеристик угла. Переменная массива объявляется типом Matrix. Обновление массива реализует функция MultiplyMatrices. В функции Draw каждая вершина треугольника объявляется типом _Point. При каждом запуске функции Draw вершины инициализируются начальными координатами точек, затем функция ApplyMatrixtoPoint обеспечивает пересчет координат в соответствии с текущими значениями массива тригонометрических характеристик угла. Поворот точек треугольника реализуется в логической системе координат, затем осуществляется преобразование в оконные координаты и рисование сторон треугольника.

По мере усложнения программы необходимо было осуществлять ее структуризацию. Очевидно, что по функциональному признаку все действия с массивами целесообразно описать в отдельном модуле.

Обратите внимание, что входными параметрами ряда функций есть не переменные, а ссылки на переменные, что обеспечивает возможность при вызове этих функций обновлять входные параметры.

Контрольные задания:

1. Согласно системы уравнений (1.2) sin и cos суммы 2-х углов, определяются по двум аргументам – sin и cos этих углов. В функции MultiplyMatrices(Matrix &dest, Matrix &left, Matrix &right), которая реализует в программе систему уравнений (1.2), используются 3 параметра (один параметр лишний). Модифицируйте функцию MultiplyMatrices, чтобы она принимала 2 параметра. Упрощенный аналог решения этого задания: Fun (&A, B)
2. Внесите изменения в программу, которые обеспечат поворот треугольника на угол (PI/10) при нажатии на левую кнопку мышки (событие WM_LBUTTONDOWN) и поворот на угол (-PI/10) при нажатии на правую кнопку (событие WM_RBUTTONDOWN).

Видео:Построение векторных диаграмм/Треугольник токов, напряжений и мощностей/Коэффициент мощностиСкачать

Анимация изображения

Мы уже обеспечили возможность поворота треугольника при каждом нажатии клавиш ← или →. Теперь поставим задачу обеспечения непрерывного вращения треугольника. Для реализации задачи необходимо обеспечить изменение угла поворота треугольника с последующим обновлением изображения. Причем, это должно выполняться в цикле.

Рассмотрим и оценим два способа циклического обновления изображения:

1. Бесконечный цикл обработки сообщений (в функции WinMain);
2. Цикл, осуществляемый через обработку события WM_TIMER.

В первом случае в бесконечный цикл помещаются 2 функции:

При запуске приложения мы получим изменение угла поворота треугольника со скоростью, которая приблизительно соответствует скорости обработки сообщений. При этом отрегулировать скорость вращения можно за счет изменения входного параметра функции AddRotation.

Если для анимации использовать бесконечный цикл обработки сообщений, то добиться точной скорости обновления изображения сложно. В WinAPI для работы со временем обычно используют сообщение WM_TIMER:

Это сообщение будет посылаться вашей программе через интервал времени, который вы зададите при создании таймера:

Создание таймера необходимо предусматривать до его использования, например – в событии WM_CREATE. Кроме этого необходимо в заголовке файла определить идентификатор таймера:

Уничтожение таймера предусматривается, когда необходимо остановить анимацию:

Контрольные вопросы и задания

1. Почему нецелесообразно использовать бесконечный цикл обработки сообщений для анимации изображения?
2. Обеспечьте при запуске программы вращение треугольника как стрелки секундомера.
3. Обеспечьте возможность запуска вращения треугольника при нажатии на клавишу P (пуск) и остановку – при нажатии на клавишу S (stop). Пример оформления события нажатия на клавишу приводится ниже:

Видео:9 класс, 15 урок, Решение треугольниковСкачать

Аффинные преобразования треугольника

Рассматриваемое ниже приложение базируется на приложении, рассмотренном выше. Отличие лишь в том, что вместо матрицы поворота используется матрица аффинных преобразований в однородных координатах. При нажатии на клавишу «T» или перемещении мыши (при нажатой клавише CTRL) матрица инициализируется конкретными значениями, задавая соответствующие преобразования треугольника.

Учитывая большое количество изменений по сравнению с приложением поворот плоскости мышью, предлагается создать новое приложение с соответствующими файлами:

Header Files

action.h
engine.h
geometry.h
matrix.h
vec.h
viewport.h

Source Files

main.cpp
action.cpp
engine.cpp
matrix.cpp
viewport.cpp

Если возникают ошибки из-за преобразования символов, то в окне свойств проекта установите «Использовать набор символов Юникода»:

Можете также скачать с моего Google-диска заархивированный файл проекта по ссылке 2d.zip. Скачивание начинается после выбора кнопки меню в правом верхнем углу открывшегося окна

Проект создан в версии Visual Studio 17. Для поздних версий (19 и выше), возможно, понадобиться пересобрать решение (кнопки меню Build>Rebuild Solution).

В файлах описаны классы, в которых сгруппированы функции и переменные для комплексного решения задачи аффинных преобразований на плоскости.

Класс Engine объединяет функцию формирования изображения (Draw) и объекты классов Action и Viewport, обеспечивающие действия по перестройке изображения, вызванной событиями нажатия на кнопки, перемещения мышки и изменения размеров окна.

Класс Action объединяет действия и данные, связанные с аффинными преобразованиями. Функция Rotate (Translate) устанавливает преобразования вращения (перемещения), опираясь на текущее и предыдущее положения мыши. Функция InitAction запоминает координаты курсора в объекте класса vec. Эти функции вызываются при событиях нажатия кнопки мышки и перемещения курсора. Функция Transform устанавливает преобразования через инициализацию коэффициентов матрицы

Класс Viewport объединяет действия и данные, связанные с изменением размеров окна, Кроме этого, в класс включена функция T, которая выполняет преобразование точек фигуры из экранных координат экрана, в логические координаты, а также, функция T_inv , которая преобразует координаты курсора из экранных координат в логические. Функция T_inv отсутствовала в приложении, рассмотренном ранее, поскольку в нем реализовывалось лишь преобразование вращения, а значение угла поворота не зависело от СК. В этом приложении с помощью курсора задается и преобразование перемещения, а оно зависит от используемой СК.

В класс Matrix была добавлена функция SetTranslationMatrix, в которой непосредственно инициализируются коэффициенты матрицы преобразований.
В классе Vec переопределяются операции с векторами. Эти операции используются в программе для определения преобразования перемещения, опираясь на текущее и предыдущее положения курсора при перемещении мыши.

Видео:Рисуем в среде программирования PascalСкачать

Контрольные задания

Задание 1. Определите коэффициенты матрицы элементарных аффинных преобразований в соответствии с вариантом задания

В каждый вариант задания включены по 3 преобразования

Пример оформления задания показан ниже на рисунке

Выполнить тестовые запуски приложения для проверки соответствия матриц заданным преобразованиям

Коэффициенты матрицы преобразования инициализируются в функции Matrix::SetTranslationMatrix1, которая определена в файле matrix.cpp. Преобразование осуществляется при нажатии клавиши T.

Задание 2. Определить произведение матриц AB, (AB)C и C(AB) и протестировать композицию элементарных преобразований запуском приложения. Преобразование осуществлять нажатием клавиши T.

Задание 3. Определить последовательность элементарных аффинных преобразований (преобразований не более 3-х), которые от начального положения треугольника приведут к заданному результату. Пример:

Для тестирования добавьте в программу дополнительные реакции на нажатие клавиш 1, 2 и 3, которые обеспечивают соответствующее элементарное преобразование:

Объявления и определения функций action->Transform вместе с входящими функциями описываются по аналогии с описанием действий при нажатии на клавишу “T”.

Задание 4. Добавьте в приложение программный код, обеспечивающий возможность переключения преобразований из глобальной СК в локальную СК. Для тестирования приложения переместите треугольник и поверните его при помощи мышки на угол 135 градусов. Если включена глобальная СК, вращение будет происходить относительно центра окна, если локальная СК – относительно вершины прямого угла.

В соответствии с алгоритмом для выполнения этого задания необходимо поменять местами текущую матрицу и матрицу, переданную в качестве параметра для функции MultiplyMatrices(Matrix &right).

Видео:Частное положение точек. Точки принадлежащие к плоскостям проекции.Скачать

learnopengl. Урок 1.4 — Hello Triangle

В OpenGL все находится в 3D пространстве, но при этом экран и окно — это 2D матрица из пикселей. Поэтому большая часть работы OpenGL — это преобразование 3D координат в 2D пространство для отрисовки на экране. Процесс преобразования 3D координат в 2D координаты управляется графическим конвейером OpenGL. Графический конвейер можно разделить на 2 большие части: первая часть преобразовывает 3D координаты в 2D координаты, а вторая часть преобразовывает 2D координаты в цветные пиксели. В этом уроке мы подробно обсудим графический конвейер и то как мы можем его использовать в плюс для создания красивых пикселей.

Есть разница между 2D координатами и пикселем. 2D координата — это очень точное представление точки в 2D пространстве, в то время когда 2D пиксель — это примерное расположение в пределах вашего экрана/окна.

Графический конвейер принимает набор 3D координат и преобразовывает их в цветные 2D пиксели на экране. Этот графический контейнер можно разделить на несколько этапов, где каждый этап — требует на вход результат работы прошлого. Все этапы эти крайне специализированы и могут с легкостью исполняться параллельно. По причине их параллельной природы большинство современных GPU имеют тысячи маленьких процессоров для быстрой обработки данных графического конвейера с помощью запуска большого количества маленьких программ на каждом этапе конвейера. Эти маленькие программы называются шейдерами.

Некоторые из этих шейдеров могут настраиваться разработчиком, что позволяет нам писать собственные шейдеры для замены стандартных. Это дает нам гораздо больше возможностей тонкой настройки специфичных мест конвейера, и именно из за того, что они работают на GPU, позволяет нам сохранить процессорное время. Шейдеры пишутся на OpenGL Shading Language (GLSL) и мы больше углубимся в него в следующем уроке.

На изображении ниже можно увидеть примерное представление всех этапов графического конвейера. Синие части описывают этапы для которых мы можем специфицировать собственные шейдеры.

Как вы видите графический конвейер содержит большое количество секций, где каждая занимается своей частью обработки вершинных данных в полностью отрисованный пиксель. Мы немного опишем каждую секцию конвейера в упрощенном виде, чтобы дать вам хорошее представление о том как работает конвейер.

На вход конвейера передается массив 3D координат из которых можно сформировать треугольники, называемого данными о вершинах; вершинные данные — это набор вершин. Вершина — это набор данных поверх 3D координаты. Эти данные представляются используя атрибуты вершины, которые могут содержать любые данные, но для упрощения будем считать что вершина состоит из 3D позиции и значения цвета.

Поскольку OpenGL хочет знать что составить из переданной ему коллекции координат и значений цвета, OpenGL требует указать какую фигуру вы хотите сформировать из данных. Хотим ли мы отрисовать набор точек, набор треугольников или просто одну длинную линию? Такие фигуры называются примитивами и передаются OpenGL во время вызова команд отрисовки. Вот некоторые из примитивов: GL_POINTS, GL_TRIANGLES и GL_LINE_STRIP.

Первый этап конвейера — это вершинный шейдер, который принимает на вход одну вершину. Основная задача вершинного шейдера — это преобразования 3D координат в другие 3D координаты (об этом немного попозже) и тот факт, что мы имеем возможность изменения этого шейдера позволяет нам выполнять некоторые основные преобразования над значениями вершины.

Сборка примитивов — это этап, принимающий на вход все вершины (или одну вершину, если выбран примитив GL_POINTS) из вершинного шейдера, которые формируют примитив и собирает из них сам примитив; в нашем случае это будет треугольник.

Результат этапа сборки примитивов передается геометрическому шейдеру. Он же в свою очередь на вход принимает набор вершин, формирующих примитивы и могут генерировать другие фигуры с помощью генерации новых вершин для формирования новых (или других) примитивов. К примеру в нашем случае он сгенерирует второй треугольник помимо данной фигуры.

Результат работы геометрического шейдера передается на этап растеризации, где результирующие примитивы будут соотноситься с пикселями на экране, формируя фрагмент для фрагментного шейдера. Перед тем как запустится фрагментный шейдер, выполняется вырезка. Она отбрасывает все фрагменты, которые находятся вне поля зрения, повышая таким образом производительность.

Фрагмент в OpenGL — это все данные, которые нужны OpenGL для того, чтобы отрисовать пиксель.

Основная цель фрагментного шейдера — это вычисление конечного цвета пикселя, а также это, чаще всего, этап, когда выполняются все дополнительные эффекты OpenGL. Зачастую фрагментный шейдер содержит всю информацию о 3D сцене, которую можно использовать для модификации финального цвета (типа освещения, теней, цвета источника света и т.д.).

После того как определение всех соответствующих цветовых значений будет закончено, результат пройдет еще один этап, который называется альфа тестирование и смешивание. Этот этап проверяет соответствующее значение глубины (и шаблона) (мы вернемся к этому позже) фрагмента и использует их для проверки местоположения фрагмента относительно других объектов: спереди или сзади. Этот этап также проверяет значения прозрачности и смешивает цвета, если это необходимо. Таким образом во время отрисовки множественных примитивов, результирующий цвет пикселя может отличаться от цвета, вычисленного фрагментным шейдером.

Как вы можете видеть, графический конвейер довольно сложен и содержит много конфигурируемых частей. Не смотря на это, мы преимущественно будем работать с вершинным и фрагментным шейдером. Геометрический шейдер не обязателен и зачастую оставляется стандартным.

В современном OpenGL вы вынуждены задать как минимум вершинный шейдер (на видеокартах не существует стандартного вершинного/фрагментного шейдера). По этой причине зачастую могут возникнуть сложности при изучении современного OpenGL, поскольку надо узнать довольно большое количество теории перед тем как нарисовать свой первый треугольник. В конце этого урока вы узнаете много нового о графическом программировании.

Видео:Математика это не ИсламСкачать

Передача вершин

Для того чтобы что-то отрисовать для начала нам надо передать OpenGL данные о вершинах. OpenGL — это 3D библиотека и поэтому все координаты, которые мы сообщаем OpenGL находятся в трехмерном пространстве (x, y и z). OpenGL не преобразовывает все переданные ему 3D координаты в 2D пиксели на экране; OpenGL только обрабатывает 3D координаты в определенном промежутке между -1.0 и 1.0 по всем 3 координатам (x, y и z). Все такие координаты называются координатами, нормализованными под устройство (или просто нормализованными).

Поскольку мы хотим отрисовать один треугольник мы должны предоставить 3 вершины, каждая из которых находится в трехмерном пространстве. Мы определим их в нормализованном виде в GLfloat массиве.

Поскольку OpenGL работает с трехмерным пространством мы отрисовываем двухмерный треугольник с z координатой равной 0.0. Таким образом глубина треугольника будет одинаковой и он будет выглядеть двухмерным.

Нормализованные координаты устройства (Normalized Device Coordinates (NDC))
После того, как вершинные координаты будут обработаны в вершинном шейдере, они должны быть нормализованы в NDC, который представляет из себя маленькое пространство, где x, y и z координаты находятся в промежутке от -1.0 до 1.0. Любые координаты, которые выходят за этот предел будут отброшены и не отобразятся на экране. Ниже вы можете увидеть заданный нами треугольник:

В отличии от экранных координат, положительное значение оси y указывает наверх, а координаты (0, 0) это центр графа, вместо верхнего левого угла.

Ваши NDC координаты будут затем преобразованы в координаты экранного пространства через Viewport с использованием данных, предоставленных через вызов glViewport. Координаты экранного пространства затем трансформируются во фрагменты и подаются на вход фрагментному шейдеру.

После определения вершинных данных требуется передать их в первый этап графического конвейера: в вершинный шейдер. Это делается следующим образом: выделяем памяти на GPU, куда мы сохраним наши вершинные данные, укажем OpenGL как он должен интерпретировать переданные ему данные и передадим GPU количество переданных нами данных. Затем вершинный шейдер обработает такое количество вершин, которое мы ему сообщили.

Мы управляем этой памятью через, так называемые, объекты вершинного буфера (vertex buffer objects (VBO)), которые могут хранить большое количество вершин в памяти GPU. Преимущество использования таких объектов буфера, что мы можем посылать в видеокарту большое количество наборов данных за один раз, без необходимости отправлять по одной вершине за раз. Отправка данных с CPU на GPU довольно медленная, поэтому мы будем стараться отправлять как можно большое данных за один раз. Но как только данные окажутся в GPU, вершинный шейдер получит их практически мгновенно.

VBO это наша первая встреча с объектами, описанными в первом уроке. Также как и любой объект в OpenGL, этот буфер имеет уникальный идентификатор. Мы можем создать VBO с помощью функции glGenBuffers:

У OpenGL есть большое количество различных типов объектов буферов. Тип VBO — GL_ARRAY_BUFFER. OpenGL позволяет привязывать множество буферов, если у них разные типы. Мы можем привязать GL_ARRAY_BUFFER к нашему буферу с помощью glBindBuffer:

С этого момента любой вызов, использующий буфер, будет работать с VBO. Теперь мы можем вызвать glBufferData для копирования вершинных данных в этот буфер.

glBufferData это функция, цель которой — копирование данных пользователя в указанный буфер. Первый ее аргумент — это тип буфера в который мы хотим скопировать данные (наш VBO сейчас привязан к GL_ARRAY_BUFFER). Второй аргумент определяет количество данных (в байтах), которые мы хотим передать буферу. Третий аргумент — это сами данные.

Четвертый аргумент определяет как мы хотим чтобы видеокарта работала с переданными ей данными. Существует 3 режима:

1. GL_STATIC_DRAW: данные либо никогда не будут изменяться, либо будут изменяться очень редко;
2. GL_DYNAMIC_DRAW: данные будут меняться довольно часто;
3. GL_STREAM_DRAW: данные будут меняться при каждой отрисовке.

Данные о позиции треугольника меняться не будут и поэтому мы выбираем GL_STATIC_DRAW. Если, к примеру, у нас был бы буфер, значение которого менялось бы очень часто — то мы бы использовали GL_DYNAMIC_DRAW или GL_STREAM_DRAW, предоставив таким образом видеокарте информацию, что данные этого буфера требуется хранить в области памяти, наиболее быстрой на запись.

Сейчас мы сохранили вершинные данные на GPU в объект буфера, называемого VBO.
Далее мы должны создать вершинный и фрагментный шейдеры для фактической обработки данных, что же, приступим.

Видео:Построение равнобедренного треугольникаСкачать

Вершинный шейдер

Вершинный шейдер — один из программируемых шейдеров. Современный OpenGL требует, чтобы был задан вершинный и фрагментный шейдеры если мы хотим что-то отрисовывать, поэтому мы предоставим два очень простых шейдера для отрисовки нашего треугольника. В следующем уроке мы обсудим шейдеры более подробно.

В начале мы должны написать сам шейдер на специальном языке GLSL (OpenGL Shading Language), а затем собрать его, чтобы приложение могло с ним работать. Вот код простейшего шейдера:

Как вы можете заметить GLSL очень похож на C. Каждый шейдер начинается с установки его версии. С OpenGL версии 3.3 и выше версии GLSL совпадают с версиями OpenGL (К примеру версия GLSL 420 совпадает с OpenGL версии 4.2). Также мы явно указали, что используем core profile.

Далее мы указали все входные вершинные атрибуты в вершинном шейдере с помощью ключевого слова in. Сейчас нам надо работать только с данными о позиции, поэтому мы указываем только один вершинный атрибут. В GLSL есть векторный тип данных, содержащий от 1 до 4 чисел с плавающей точкой. Поскольку вершины имеют трехмерные координаты то и мы создаем vec3 с названием position. Также мы явно указали позицию нашей переменной через layout (location = 0) позже вы увидите, зачем мы это сделали.

Vector
В графическом программировании мы довольно часто используем математическую концепцию вектора, поскольку она отлично представляет позиции/направления в любом пространстве, а также обладает полезными математическими свойствами. Максимальный размер вектора в GLSL — 4 элемента, а доступ к каждому из элементов можно получить через vec.x, vec.y, vec.z и vec.w соответственно. Заметьте, что компонента vec.w не используется в качестве позиции в пространстве (мы же работает в 3D, а не в 4D), но она может быть полезна при работе с разделением перспективы (perspective division). Мы обсудим вектора более глубоко в следующем уроке.

Для обозначения результата работы вершинного шейдера мы должны присвоить значение предопределенной переменной gl_Position, которая имеет тип vec4. После окончания работы main функции, что бы мы не передали в gl_Position, оно будет использовано в качестве результата работы вершинного шейдера. Поскольку наш входной вектор трехмерный мы должны преобразовать его в четырехмерный. Мы можем сделать это просто передав компоненты vec3 в vec4, а компоненте w задать значение 1.0f (Мы объясним почему так позже).

Этот вершинный шейдер, вероятно, самый простой шейдер который только можно придумать, поскольку он не обрабатывает никаких данных, а просто передает эти данные на выход. В реальных приложениях входные данные не нормализованы, поэтому в начале их требуется нормализовать.

Видео:Торговля на бирже. Трейдеры не хотят, что бы вы это знали.Скачать

Сборка шейдера

Мы написали исходный код шейдера (хранимый в C строке), но чтобы этим шейдеров мог пользоваться OpenGL, его надо собрать.

В начале мы должны создать объект шейдера. А поскольку доступ к созданным объектам осуществляется через идентификатор — то мы будем хранить его в переменной с типом GLuint, а создавать его будем через glCreateShader:

Во время создания шейдера мы должны указать тип создаваемого шейдера. Поскольку нам нужен вершинный шейдер, мы указываем GL_VERTEX_SHADER.

Далее мы привязываем исходный код шейдера к объекту шейдера и компилируем его.

Функция glShaderSource в качестве первого аргумента принимает шейдер, который требуется собрать. Второй аргумент описывает количество строк. В нашем случае строка лишь одна. Третий параметр — это сам исходный код шейдера, а четвертый параметр мы оставим в NULL.

Скорее всего вы захотите проверить успешность сборки шейдера. И если шейдер не был собран — получить ошибки, которые возникли во время сборки. Проверка на наличие ошибок происходит следующим образом:

Для начала мы объявляем число для определения успешности сборки и контейнер для хранения ошибок (если они появились). Затем мы проверяем успешность с помощью glGetShaderiv. Если сборка провалится — то мы сможем получить сообщение об ошибки с помощью glGetShaderInfoLog и вывести эту ошибку:

После этого, если не возникло никаких ошибок компиляции — то шейдер будет собран.

Видео:СЛОЖИТЕ ДВА КОРНЯСкачать

Фрагментный шейдер

Цвет в компьютерной графике представляется как массив из 4 значений: красный, зеленый, синий и прозрачность; такая компонентная база называется RGBA. Когда мы задаем цвет в OpenGL или в GLSL мы задаем величину каждого компонента между 0.0 и 1.0. Если к примеру мы установим величину красного и зеленого компонентов в 1.0f, то мы получим смесь этих цветов — желтый. Комбинация из 3 компонентов дает около 16 миллионов различных цветов.

Фрагментный шейдер на выход требует только значения цвета, являющийся 4 компонентным вектором. Мы можем указать выходную переменную с помощью ключевого слова out, а назовем мы эту переменную color. Затем мы просто устанавливаем значение этой переменной vec4 с непрозрачным оранжевым цветом.

Процесс сборки фрагментного шейдера аналогичен сборке вершинного, только требуется указать другой тип шейдера: GL_FRAGMENT_SHADER:

Оба шейдера были собраны и теперь только осталось связать их в программу, чтобы мы могли использовать их при отрисовке.

Видео:Треугольник с перпендикулярными медианами. Как найти третью сторону по известным двум?Скачать

Шейдерная программа

Шейдерная программа — это объект, являющийся финальным результатом комбинации нескольких шейдеров. Для того, чтобы использовать собранные шейдеры их требуется соединить в объект шейдерной программы, а затем активировать эту программу при отрисовке объектов, и эта программа будет использоваться при вызове команд отрисовки.

При соединении шейдеров в программу, выходные значения одного шейдера сопоставляются с входными значениями другого шейдера. Вы также можете получить ошибки во время соединения шейдеров, если входные и выходные значения не совпадают.

Создать программу очень просто:

Функция glCreateProgram создает программу и возвращает идентификатор этой программы. Теперь нам надо присоединить наши собранные шейдеры к программе, а затем связать их с помощью glLinkProgram:

Этот код вполне описывает сам себя. Мы присоединяем шейдеры к программе, а потом связываем их.

Также как и со сборкой шейдера мы можем получить успешность связывания и сообщение об ошибке. Единственное отличие — что вместо glGetShaderiv и glGetShaderInfoLog мы используем:

Для использования созданной программы надо вызвать glUseProgram:

Каждый вызов шейдера и отрисовочных функций будет использовать наш объект программы (и соответственно наши шейдеры).

Ах да, не забудьте удалить созданные шейдеры после связывания. Они нам больше не понадобятся.

На данный момент мы передали GPU вершинные данные и указали GPU как их обрабатывать. Мы почти закончили. OpenGL еще на знает как представить вершинные данные в памяти и как соединять вершинные данные в аттрибуты вершинного шейдера. Что же, приступим.

Связывание вершинных атрибутов

Вершинный шейдер позволяет нам указать любые данные в каждый атрибут вершины, но это не значит, что нам придется указывать какой элемент данных относится к какому атрибуту. Это означает, что мы должны сообщить как OpenGL должен интерпретировать вершинные данные перед отрисовкой.

Формат нашего вершинного буфера следующий:

• Информация о позиции хранится в 32 битном (4 байта) значении с плавающей точкой;
• Каждая позиция формируется из 3 значений;
• Не существует никакого разделителя между наборами из 3 значений. Такой буфер называется плотно упакованным;
• Первое значение в переданных данных — это начало буфера.

Зная эти особенности мы можем сообщить OpenGL как он должен интерпретировать вершинные данные. Делается это с помощью функции glVertexAttribPointer:

У функции glVertexAttribPointer имеет немного параметров, давайте быстро пробежимся по ним:

Первый аргумент описывает какой аргумент шейдера мы хотим настроить. Мы хотим специфицировать значение аргумента position, позиция которого была указана следующим образом: layout (location = 0).

Следующий аргумент описывает размер аргумента в шейдере. Поскольку мы использовали vec3 то мы указываем 3.

Третий аргумент описывает используемый тип данных. Мы указываем GL_FLOAT, поскольку vec в шейдере использует числа с плавающей точкой.

Четвертый аргумент указывает необходимость нормализовать входные данные. Если мы укажем GL_TRUE, то все данные будут расположены между 0 (-1 для знаковых значений) и 1. Нам нормализация не требуется, поэтому мы оставляем GL_FALSE;

Пятый аргумент называется шагом и описывает расстояние между наборами данных. Мы также можем указать шаг равный 0 и тогда OpenGL высчитает шаг (работает только с плотно упакованными наборами данных). Как выручить существенную пользу от этого аргумента мы рассмотрим позже.

Каждый атрибут вершины получает значение из памяти, управляемой VBO, которая в данный момент является привязанной к GL_ARRAY_BUFFER. Соответственно если бы мы вызвали glVertexAttribPointer с другим VBO — то вершинные данные были бы взяты из другого VBO.

После того как мы сообщили OpenGL как он должен интерпретировать вершинные данные мы должны включить атрибут с помощью glEnableVertexAttribArray. Таким образом мы передадим вершинному атрибуту позицию аргумента. После того как мы все настроили мы инициализировали вершинные данные в буфере с помощью VBO, установили вершинный и фрагментный шейдер и сообщили OpenGL как связать вершинный шейдер и вершинные данные. Отрисовка объекта в OpenGL будет выглядеть как-то так:

Мы должны повторять этот процесс при каждой отрисовке объекта. Кажется что это не очень сложно, но теперь представьте, что у вас более 5 вершинных атрибутов и что-то в районе 100 различных объектов. И сразу постоянная установка этих конфигураций для каждого объекта становится дикой рутиной. Вот бы был какой-нибудь способ для хранения всех этих состояний и что нам надо было бы только привязаться к какому-нибудь состоянию для отрисовки…

Vertex Array Object

Core OpenGL требует чтобы мы использовали VAO для того чтобы OpenGL знал как работать с нашими входными вершинами. Если мы не укажем VAO, OpenGL может отказаться отрисовывать что-либо.

VAO хранит следующие вызовы:

• Вызовы glEnableVertexAttribArray или glDisableVertexAttribArray.
• Конфигурация атрибутов, выполненная через glVertexAttribPointer.
• VBO ассоциированные с вершинными атрибутами с помощью glVertexAttribPointer

Процесс генерации VAO очень похож на генерацию VBO:

Для того, чтобы использовать VAO все что вам надо сделать — это привязать VAO с помощью glBindVertexArray. Теперь мы должны настроить/привязать требуемые VBO и указатели на атрибуты, а в конце отвязать VAO для последующего использования. И теперь, каждый раз когда мы хотим отрисовать объект мы просто привязываем VAO с требуемыми нам настройками перед отрисовкой объекта. Выглядеть это все должно примерно следующим образом:

В OpenGL отвязывание объектов это обычное дело. Как минимум просто для того, чтобы случайно не испортить конфигурацию.

Вот и все! Все что мы делали на протяжении миллионов страниц подводило нас к этому моменту. VAO, хранящее вершинные атрибуты и требуемый VBO. Зачастую, когда у нас есть множественные объекты для отрисовки мы в начале генерируем и конфигурируем VAO и сохраняем их для последующего использования. И когда надо будет отрисовать один из наших объектов мы просто используем сохраненный VAO.

Треугольник, которого мы так ждали

Для отрисовки наших объектов OpenGL предоставляет нам функцию glDrawArrays. Она использует активный шейдер и установленный VAO для отрисовки указанных примитивов.

Функция glDrawArrays принимает в качестве первого аргумента OpenGL примитив, который требуется отрисовать. Поскольку мы хотим отрисовать треугольник и так как мы не хотим врать вам, мы указываем GL_TRIANGLES. Второй аргумент указывает начальный индекс массива с вершинами, который мы хотим отрисовать, мы просто оставим 0. Последний аргумент указывает количество вершин для отрисовки, нам требуется отрисовать 3 (длина одного треугольника — 3 вершины).

Теперь можно собрать и запустить написанный код. Вы увидите следующий результат:

Исходный код можно найти тут.

Если ваш результат отличается то, вероятно, вы где-то ошиблись. Сравните ваш код с представленным выше исходным кодом.

Element Buffer Object

Заметка от переводчика
Как заметил пользователь proydakov, данный объект еще называют Index Buffer Object, соответственно IBO.

Соответственно надо будет объявить следующий набор вершин:

Как вы можете заметить: мы два раза указали нижнюю правую и верхнюю левую вершину. Это не очень рациональное использование ресурсов, поскольку мы можем описать прямоугольник 4 вершинами вместо 6. Проблема становится еще более весомой, когда мы имеем дело с бОльшими моделями у которых может быть более 1000 треугольников. Самое правильное решение этой проблемы — это хранить только уникальные вершины, а потом отдельно указывать порядок в котором мы хотим чтобы производилась отрисовка. В нашем случае нам бы потребовалось хранить только 4 вершины, а затем указать порядок в котором их надо отрисовать. Было бы отлично, если бы OpenGL предоставлял такую возможность.

К счастью EBO это именно то, что нам нужно. EBO — это буфер, вроде VBO, но он хранит индексы, которые OpenGL использует, чтобы решить какую вершину отрисовать. Это называется отрисовка по индексам (indexed drawing) и является решением вышеуказанной проблемы. В начале нам надо будет указать уникальные вершины и индексы для отрисовки их как треугольников:

Как вы можете заметить, нам потребовалось только 4 вершины вместо 6. Затем нам надо создать EBO:

Также как и с VBO мы привязываем EBO и копируем индексы в этот буфер через glBufferData. Также, как и с VBO мы помещаем вызовы между командами связывания и развязывания (glBindBuffer(GL_ELEMENT_ARRAY_BUFFER, 0), только в этот раз типом буфера является GL_ELEMENT_ARRAY_BUFFER.

Заметьте, что сейчас мы передаем GL_ELEMENT_ARRAY_BUFFER в качестве целевого буфера. Последнее что нам осталось сделать — это заменить вызов glDrawArrays на вызов glDrawElements для того, чтобы указать, что мы хотим отрисовать треугольники из буфера с индексами. Когда используется glDrawElements производится отрисовка из привязанного в данный момент EBO:

Первый аргумент описывает примитив, который мы хотим отрисовать, также как и в glDrawArrays. Второй аргумент — это количество элементов, которое мы хотим отрисовать. Мы указали 6 индексов, поэтому мы передаем функции 6 вершин. Третий аргумент — это тип данных индексов, в нашем случае — это GL_UNSIGNED_INT. Последний аргумент позволяет задать нам смещение в EBO (или передать сам массив с индексами, но при использовании EBO так не делают), поэтому мы указываем просто 0.

Функция glDrawElements берет индексы из текущего привязанного к GL_ELEMENT_ARRAY_BUFFER EBO. Это означает, что если мы должны каждый раз привязывать различные EBO. Но VAO умеет хранить и EBO.

VAO хранит вызовы glBindBuffer, если целью является GL_ELEMENT_ARRAY_BUFFER. Это также означает, что он хранит и вызовы отвязывания, так что удостоверьтесь, что вы не отвязали ваш EBO перед тем как отвязать VAO, иначе у вас вообще не будет привязанного EBO.

В результате вы получите примерно такой код:

После запуска программа должна выдать следующий результат. Левое изображение выглядит именно так как мы и планировали, правое изображение — это прямоугольник отрисованный в режиме wireframe. Как можно увидеть этот четырехугольник построен из 2 треугольников.

Для того чтобы отрисовать ваши треугольники в этом режиме, укажите OpenGL, как отрисовывать примитивы с помощью glPolygonMode(GL_FRONT_AND_BACK, GL_LINE). Первый аргумент указываем, что мы хотим отрисовывать переднюю и заднюю части всех треугольников, а второй аргумент, что мы хотим отрисовывать только линии. Для того, чтобы вернуться к начальной конфигурации — вызовите glPolygonMode(GL_FRONT_AND_BACK, GL_FILL).

Если у вас возникли какие-либо проблемы, пробегитесь по уроку, возможно вы что-то забыли. Также вы можете сверится с исходным кодом.

Если у вас все получилось — то поздравляю, вы только что прошли через одну из самых сложных частей изучения современного OpenGL: вывод первого треугольника. Эта часть такая сложная, поскольку требует определенный набор знаний перед тем как появится возможно отрисовать первый треугольник. Благо мы уже прошли через это и последующие уроки должны быть проще.

Дополнительные ресурсы

Упражнения

Для закрепления изученного предложу несколько упражнений:

1. Попробуйте отрисовать 2 треугольника один за другим с помощью glDrawArrays с помощью добавления бОльшего количества вершин. Решение
2. Создайте 2 треугольника с использованием 2 различных VAO и VBO. Решение
3. Создайте второй фрагментный шейдеры и чтобы он выводил желтый цвет. И сделайте так, чтобы второй треугольник был желтого цвета. Решение