Готлоб фреге логический треугольник

Что такое семиотика? Что такое треугольник Фреге? Смысл, знак и значение рассмотрим в рамках статьи. Чтобы разобраться с понятием, недостаточно прочитать определение термина. Нужно понимать, чем именно занимался создатель идеи.

Видео:Треугольник Фреге | Дефляционная теория истиныСкачать

Кому принадлежит авторство?

Идея, известная как треугольник Фреге, принадлежит немецкому математику, также занимавшемуся философией и логикой. Звали его Фридрихом Людвигом Готлобом Фреге. Жил и трудился этот человек на стыке XIX и XX столетий.

Родился ученый в семье школьного преподавателя. Образование Фреге получил в Йенском университете, а диссертацию защитил в Геттингене. После ее защиты вернулся в Йену, где вскоре получил должность приват-доцента на одной из кафедр местного университета.

Видео:[Т.А.] Треугольник Фреге. Введение в семиотику.Скачать

В чем значение работ этого ученого?

Треугольник Фреге – далеко не единственная идея немецкого логика и математика, имевшая значение для развития философской мысли. Однако признание они получили в основном за счет развития и популяризации их учениками и последователями. Одним из них был Рудольф Карнал, немало сделавший для развития философии и идей логического позитивизма.

Основное значение трудов Фреге в том, что в них ученый пересмотрел ряд математических закономерностей, подойдя к ним с совершенно новых позиций. Его работа Begriffsschrift, что в переводе с русского означает «исчисление понятий», увидевшая свет в 1879 году, практически стала началом новой эры в истории развития логики.

Также именно этот ученый впервые дал определения таким понятиям, как «значение», «смысл» и описал разницу между ними. Именно это и известно в современном мире как семантический треугольник Фреге.

Видео:3.2. Знак. Теория Г. Фреге.Скачать

Что же это такое?

Его называют по-разному – понятием, теорией, идеей, термином. Треугольник Фреге – понятие, символическое изображение, определение, направление и даже научная закономерность одновременно.

Это логическое построение, объясняющее различия между значением и смыслом любого понятия. С помощью этой «фигуры» можно рассмотреть любую предметную область. Применима данная формула и для искусства, наук, информационного поля, языков и прочего.

Видео:Маргинал поясняет Курпатову за треугольник ФрегеСкачать

Суть понятия и его графического отображения

Логика треугольника Фреге — во взаимной непрерываемой связи трех основных компонентов, именуемых:

Эти три компонента являются вершинами фигуры, а линии, их соединяющие, выражают взаимное влияние одного на другое.

Видео:Фреге. Знание. Истина.Скачать

Что подразумевается под названиями вершин?

Треугольник Фреге, семиотика которого неразрывно связана с его основными элементами, является универсальной формулой постоянных закономерностей, применимой для любой области. Разумеется, в зависимости от сферы применения меняется суть того, что подразумевается под наименованиями вершин графического символического отображения.

Значение – это определенная область, соотносимая с наименованием предмета рассмотрения. Непосредственно сам рассматриваемый компонент – это знак или же имя. Термин «имя» нередко используют при анализе по формуле «треугольник Фреге» деятельности людей в науке, искусстве или иной сфере. Применяют его и для рассмотрения так называемых «одушевленных явлений».

Смысл – это какой-либо конкретный, определенный, отдельно взятый аспект в рассматриваемой области, непосредственно связанный с предметом анализа.

Видео:3.4. Знак. Заключение. Референт и денотат. Треугольник Огдена - Ричардса.Скачать

В чем научное значение этой формулы?

Логический треугольник Фреге – революционное открытие, которое еще не полностью оценено и имеет безграничный потенциал.

Выведение данной закономерности позволило объединить математические законы, философию и логическое построение и сделать возможным их практическое применение в любой жизненной сфере.

Кроме этого, данное открытие легло в основу многих научных трудов, самыми известными из которых являются:

• теоремы о неполноте Курта Фридриха Геделя;
• теория описаний Бертрана Артура Уильяма Рассела.

Теоремы о неполноте развивают представление о математической логике, а работа графа Рассела касается философских вопросов.

Видео:Готлоб ФрегеСкачать

Что такое семиотика?

Данный термин нередко употребляется в общем контексте, когда речь заходит о треугольнике Фреге. Кратко понятие «семиотика» представить достаточно сложно, поскольку оно является весьма объемным и многозначным.

Как говорят в народе, в двух словах термин можно объяснить следующим образом. Семиотика – это обобщающая теория взаимоотношений ключевых элементов в знаковых системах. Именно с ее помощью треугольник Фреге становится универсальной формулой, применимой к любой области человеческой жизнедеятельности или же иной сфере.

Видео:Аналитическая философия Готлоба ФрегеСкачать

К чему сводится взаимосвязь между основными элементами?

Как правило, взаимосвязь между вершинами треугольника или основными элементами данной формулы сводится к следующему:

• отношение знака к рассматриваемой области, обозначение рамок анализа;
• влияние этого же символа на понятие о нем, смысл.

То есть в основе всех взаимосвязей лежит знак или имя. Эта вершина треугольника является отправной точкой, стартом для всех остальных положений, заключений, логических цепей и прочего.

Иными словами, без наличия знака невозможно существование самой формулы, этот символ – первичен. Однако остальные вершины оказывают на него собственное влияние.

Эту особенность, иллюстрирующую взаимосвязь всех трех основных составляющих, можно рассмотреть на примере использования людьми псевдонимов. Допустим, в качестве знака в формуле взято имя Марк Твен. Разумеется, в качестве значения, то есть ассоциирующейся или связанной со знаком области, выступит литература. Под смыслом же будет подразумеваться нечто, связанное с вкладом писателя в нее, значением его произведений. Однако если в качестве знака будет взято имя Сэмюэл Лэнгхорн Клеменс, то ассоциативного восприятия с литературной деятельностью не возникнет. Соответственно, понятия «значения» и «смысла» окажутся иными. Хотя Клеменс и Твен – один человек.

Эта особенность нередко называется «частным случаем». Для устранения погрешностей в применении формулы Фреге, обусловленных подобными случайностями, используется семиотика.

Видео:Смысл и понимание в гуманитарных исследованиях — Виталий КуреннойСкачать

Какими могут быть отношения между основными элементами?

Каждый из трех основных, ключевых элементов или же вершин в этом треугольнике одновременно является как самостоятельным понятием, оказывающим влияние на остальные компоненты, так и может выступать в качестве посредника между своими соседями.

Это означает, что каждый из главных элементов обеспечивает существование не только себя, но и других. Иными словами, ни одно явление не рассматривается без контекста, а он, в свою очередь, оказывает влияние на понимание вызвавшей его причины.

Примером этого может быть ясный день — природное явление, обусловленное активностью Солнца. Однако оно было бы недостижимо на отдельно взятой территории планеты без вращения Земли вокруг своей оси.

Более наглядно и упрощенно эти отношения между ключевыми элементами, вершинами треугольника, выглядят в обычной жизни. К примеру, торговля. Для всех очевидно соотношение и взаимное влияние таких понятий, как «спрос», «предложение», «возможность». А они тоже подчиняются закономерности, выверенной немецким логистом, философом и математиком.

Видео:Евгений Логинов. Аналитическая философия: Готлоб Фреге.Скачать

Треугольник отражает объективную реальность или нет?

Этот вопрос является предметом для дискуссий в научных кругах не первое десятилетие. Действительно, с одной стороны, треугольник Фреге – математическая формула, основанная на законах простых, логичных и вполне объективных. С другой же стороны, в нем немало переменных аспектов, нюансов, влияющих на результаты и само содержание. Да и все логические цепи, составляющие взаимоотношения, не являются тем, что можно измерить или же потрогать. Они выстроены в сознании, то есть это плод работы мозга, мыслительной деятельности. Следовательно, к объективной реальности отношения данная формула не имеет.

Однако все не столь однозначно, как кажется на первый взгляд. Рассматриваемая, анализируемая по формуле треугольника вещь, явление, предмет или же что-либо еще – это неизменно объективная данность, существующая в реальности. Но человек осмысливает эту данность. То есть рассматривает и анализирует какой-либо предмет через собственное представление о нем, восприятие. Это, в свою очередь, основывается на имеющихся знаниях. Логические умозаключения же строятся не только на базе информации об анализируемом явлении, но и с учетом жизненного опыта, культурных ценностей и даже менталитета.

Это означает, что в отношении одного и того же явления, к примеру, грозы, разные люди сделают неодинаковые выводы, имея аналогичные исходные данные. Они выстроят в сознании различные логические цепи. То есть понимание сути такого явления природы, как гроза, у человека, проживающего в эпоху каменного века, в библейские времена и в наши дни будет разным.

В этом заключается парадокс треугольника Фреге. Практическое применение данной формулы в различных условиях неизменно приводит к особенным результатам. Причем они всегда верны для тех условий, в рамках которых применялась формула.

В этом и заключается основная ценность, которую представляет собой закономерность, именуемая «треугольник Фреге». Ею можно пользоваться на практике в любых условиях, независимо ни от каких социальных особенностей или уровня развития общества.

Видео:Животные без прав. Гуманитарные науки под контролем. Шепелин*/Утро с Воробьевой и Аникиной /21.01.24Скачать

Семантический треугольник Готлоба Фреге

Как связаны знак, смысл и значение

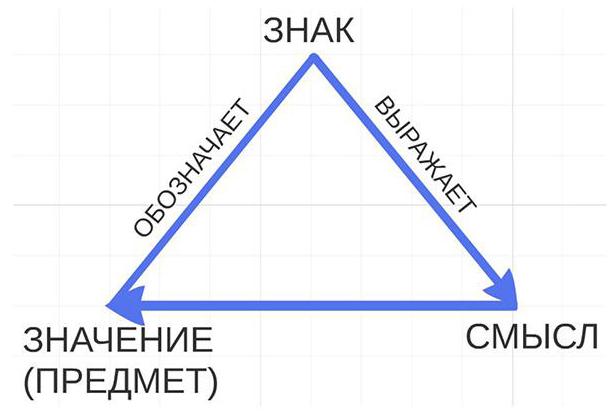
Что это: В статье «Смысл и значение» (Über Sinn und Bedeutung, 1892) Готлоб Фреге изложил свое понимание семантики знаковых выражений. Хотя в самом тексте работы такой схемы нет, она традиционно используется для иллюстрации семантической модели Фреге. Текст этой статьи, наряду с такими текстами, как «Функция и понятие» (Funktion und Begriff, 1891), «Понятие и предмет» (Über Begriff und Gegenstand, 1892), «Мысль» (1918), является одной из главных работ для современной аналитической философии языка и языковой семантики. Эти работы заложили основу для современной логики — логики предикатов, существенно отличающейся от традиционной аристотелевской логики силлогизмов. Последняя, как долго считалось, не может быть улучшена, однако Фреге совершил эту революцию в логике, предложив не только новую семантическую модель языковых выражений, но и новую трактовку понятий (или, согласно аристотелевской терминологии, предикатов), рассматривая их как функции: «Понятие есть функция аргумента, значение которой всегда есть истинностное значение» («Функция и понятие»).

Получившаяся сематическая модель — это побочный результат работы Фреге, сформулировавшего так называемую программу логицизма. Логицизм рассматривает математику (Фреге работал с арифметикой) как раздел и ответвление формальной логики. Из этой программы, в частности, следует, что все арифметические формулы являются аналитическими суждениями, то есть тавтологиями. Позднее в разработку этой программы Фреге включились Альфред Норт Уайтхед и Бертран Рассел, которые, однако, использовали более простой и удобный символический аппарат логического исчисления. Как раз по этой причине их работа в этой области сразу получила широкую известность, в отличие от «исчисления понятий» (Begriffsschrift) Фреге, оперировавшего не очень наглядной и удобной символикой.

Семантический треугольник Фреге — это революционный шаг по отношению к классическим семантическим моделям, оперирующим только двумя элементами: знаком (означающим) и предметом, который обозначен этим знаком (означаемым, или, в терминологии Фреге, значением). Фреге вводит третью семантическую инстанцию, которую он называет «смысл»: знак относится к означаемому не напрямую, а опосредованно, через перспективу смысла. Эта терминология Фреге, впрочем, не очень удобна и даже вызывала некоторую путаницу в ранней англоязычной аналитической философии, поскольку понятие «смысл» (Sinn) переводилось то термином sense, то термином meaning. Позднее Эдмунд Гуссерль предложил использовать понятие «смысл» и «значение» как синонимы, а означаемое называть «предмет», как это и отражено на приведенной выше схеме. Существует и ряд других позднейших терминологических вариаций этой триады.

Чем это интересно для науки: Данная семантическая модель дает решение множества трудных проблем в различных областях науки. Например, из нее следует, что знак может иметь смысл, но не иметь значения (или предмета, который он обозначает). Не имея предмета, к которому он относится, знак тем не менее имеет смысл (если только это не бессмысленная конструкция, нарушающая правила семантики). Такими знаками в математике является, например, число π или число √2. Оба эти числа представляют собой так называемые иррациональные числа: они являются бесконечными непериодическими дробями (то есть мы не можем вычислить, какое число появится в этой дроби следующим). Метафорически их можно представить как провалы и разрывы на числовой прямой: они не обозначают никакого определенного числа, поскольку их значение будет вычисляться бесконечно, поэтому мощность новых вычислительных устройств традиционно опробуют, доходя до какого-то очередного знака после запятой в значении числа π: в рамках одного из таких рекордных вычислений было установлено, что десятитриллионная цифра числа π равна пяти. Однако это не мешает нам использовать такие знаки чисел в практике вычислений и подсчетов. Семантика Фреге разрешает этот парадокс, указывая на то, что знак не является бессмысленным, даже если он ничего не обозначает. Несуществование предметов, которые обозначают такие выражения, как «круглый квадрат», не мешает нам понимать и считать осмысленными высказывания вроде: «Круглых квадратов не существует».

Непосредственно в работе «Смысл и значение» Фреге использует эту модель для того, чтобы ответить на вопрос, каким образом получается так, что выражения типа a = b мы считаем принципиально отличающимися от выражений типа a = a. Если мы оперируем двухчастной семантической моделью, то получается, что в случае синтетических суждений (a = b), а не аналитических тавтологий (a = a) мы лишь иным образом именуем один и тот же предмет. Однако на деле мы считаем, что синтетические суждения дают нам прирост знания о предмете, и тут дело не только в смене знака, обозначающего какой-то предмет. Действительно, если бы дело было только в названии, то выражение «вода — это H2O», сформулированное Лавуазье и рядом других его современников, ничем бы не отличалось от выражения «вода — это сепулька», если мы просто установим конвенцию, согласно которой слово «сепулька» будет считаться синонимом слова «вода». Однако мы считаем выражение «вода — это H2O» серьезным открытием, а не просто заменой одного знака другим, которому мы приписали свойство синонимичности по отношению к первому.

Из семантической модели Фреге следует, что мы достигаем здесь существенного прироста знания, так как связываем с одним и тем же предметом выражения (знаки), имеющие разный смысл, причем связь смыслов этих знаков с одним и тем же предметом не является очевидной. Например, во многих языках есть выражение «Утренняя звезда» (или Morgenstern) и «Вечерняя звезда» (или Abendstern), из чего следует, что люди традиционно считали, что это разные небесные тела. Понадобилось много тысячелетий, чтобы люди с помощью астрономических наблюдений и астрономических моделей установили, что оба эти имени относятся к одному и тому же предмету — планете Венера.

Примеры, которые мы рассмотрели, относятся к именам собственным или к наименованиям веществ, грамматическая категория имен нарицательных образует у Фреге сферу понятий-функций.

В случае более сложных знаков, а именно высказываний, которые обладают тем свойством, что могут быть истинными или ложными, то есть в логическим отношении представляют собой суждения, семантическая конфигурация Фреге определяется в следующих терминах: смыслом суждений является мысль, а значением суждений — их истинностное значение, которое может быть одним из двух — истиной или ложью. Из этого следует удивительный вывод: все суждения обозначают только два предмета. Используя метафору из мира человеческого восприятия, можно пояснить это так: любое суждение относится к миру в целом и либо соответствует ему, либо нет.

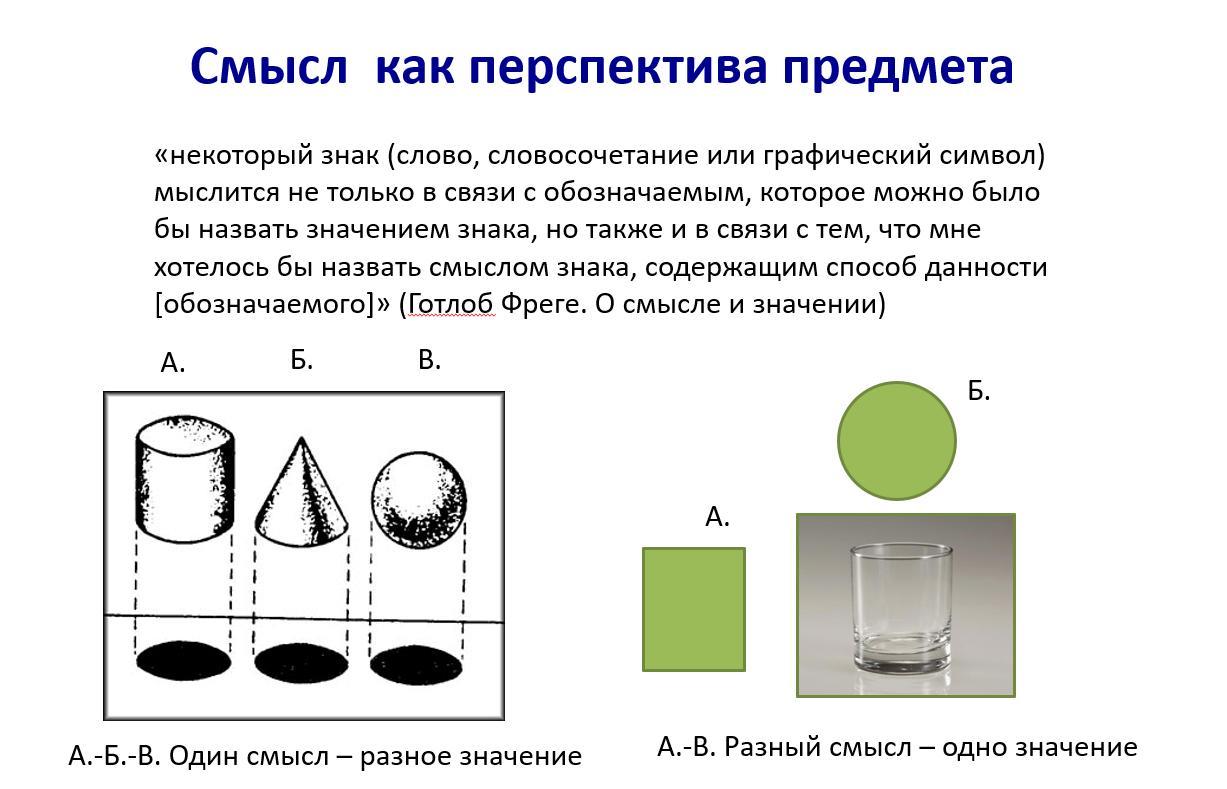
Понятие смысла Фреге раскрывает через перспективисткую метафору: смысл — это способ данности предмета: «некоторый знак (слово, словосочетание или графический символ) мыслится не только в связи с обозначаемым, которое можно было бы назвать значением знака, но также и в связи с тем, что мне хотелось бы назвать смыслом знака, содержащим способ данности [обозначаемого]» (Готлоб Фреге. Смысл и значение). Стоит добавить, что предмет внешнего мира всегда дан человеку в какой-то перспективе или каком-то ракурсе (в феноменологии Гуссерля каждая такая перспектива или ракурс предмета внешнего мира называется Abschattung, дословно — оттенок), причем число этих перспектив в отношении одного предмета может варьироваться до бесконечности. Из этого следует, что с любым предметом возможно связать также и бесконечное число смыслов.

Анализируя различные характеристики и параметры смысла, Фреге приходит к следующим его ключевым характеристикам:

• Смысл есть у знаков, не обозначающих никаких предметов.
• С одним предметом может быть связано множество смыслов.
• Зная смысл знака или выражения, мы не всегда можем установить предмет, который этот знак обозначает. Установление такого соответствия как раз и составляет сущность, например, научного открытия.
• Смыл объективен и интерсубъективен, доступен для точного понимания разным участникам коммуникации.
• Смысл не является психологическим образованием индивида, его субъективным представлением индивида о предмете.
• В некоторых контекстах (названных позднее экстенсиональными) различия в смысле знаков не играют никакой роли. Мы можем свободно заменять одни знаки другими, если только они обозначают один и тот же предмет. В других контекстах (интенсиональных) мы должны учитывать также и роль смысла. Например, в современной научной или научно-популярной литературе выражения «Солнце» и «центральное тело Солнечной системы» будут полностью взаимозаменяемы: если вместо «Вокруг Солнца вращается восемь планет» мы сегодня скажем: «Вокруг центрального тела Солнечной системы вращается восемь планет», то эта замена терминов не приведет к изменению истинности нового суждения (то есть будет соблюден принцип salva veritate — сохранения истинности). Но если мы попробуем произвести ту же замену в высказывании: «Птолемей считал, что Солнце вращается вокруг Земли», то получим абсурдное с позиций современной науки высказывание: «Птолемей считал, что Солнце вращается вокруг центрального тела Солнечной системы». Ученые, которые стремились вслед за Фреге разрабатывать идеально-строгие научные языки, например Рудольф Карнап, стремились избежать в них эффекта интенсиональных контекстов.

Зачем это знать: Без знания треугольника Фреге невозможно понимание проблематики современной логики и математики, современной аналитической философии, современной феноменологии, современной герменевтики, современной исторической семантики и множества других научных и философских направлений. Хотя не все принимают семантическую модель Фреге, дискуссии по этому поводу всегда включают ее рассмотрение. В области исследований культуры эта модель является фундаментальной, поскольку культурология занимается именно смысловым контекстом существования и поступков человека.

Изучая смыслы, которые человек связывает с миром в ту или иную эпоху, мы, согласно этой семантической концепции, имеем дело с объективным материалом, не имеющим ничего общего с произвольностью индивидуальных переживаний, несмотря на то что эти смыслы могут относится к совершенно фантастическим или несуществующим предметом. Поэтому историко-культурологические исследования могут быть столь же точными, как и исследования в сфере математики, хотя эта точность и своего рода, поскольку не ограничена лишь миром математических предметов.

Видео:«Сумма маркетинга»: Семантический треугольникСкачать

Урок 1. Логический анализ языка

Первый урок нашего курса мы посвятим сложной, но очень важной теме – логическому анализу языка. Сразу стоит оговориться, что эта тема многим может показаться абстрактной, нагруженной терминологией, неприменимой на практике. Не пугайтесь! Логический анализ языка – это основа любой логической системы и правильного рассуждения. Те термины, которые мы здесь узнаем, станут нашим логическим алфавитом, без знания которого просто нельзя пойти дальше, но постепенно мы научимся пользоваться им с лёгкостью.

Во введении к курсу было сказано, что логика концентрируется только на той части человеческого знания, которая выражена в языковой форме. Всем известно, что язык – это основной канал коммуникации между людьми, главный способ передачи информации и трансляции знаний. При этом язык – настолько тонкий инструмент, что он позволяет не только наилучшим образом выражать и передавать наши мысли, но и скрывать их, запутывать, обманывать. Поэтому логика ставит перед собой задачу прояснить работу языка. Не занимается ли тем же самым языкознание? И да, и нет. Безусловно, филологи проясняют, как работает язык на разных уровнях: фонетическом, лексическом, синтаксическом. Также они анализируют регулярности в языковом употреблении, и на основе этого анализа разрабатываются правила орфографии, грамматики, пунктуации, произношения. Эти правила призваны унифицировать использование языка и сделать его более лёгким и понятным.

Логики под прояснением работы языка понимают нечто совершенно иное. В отличие от языкознания, логика стремится как можно больше абстрагироваться от конкретной языковой оболочки и содержания высказываний и перейти к независимым от них универсальным логическим законам и правилам рассуждения. Философ и логик Людвиг Витгенштейн говорил, что язык переодевает мысли (Витгенштейн Л. Логико-философский трактат. М.: Канон+, 2008, с. 72). Так вот, задача логического анализа языка снять языковую одежду и выявить тот скелет или каркас, который под ней скрыт. Логики называют этот скелет логической формой. Если говорить просто, логическая форма – это то, что остаётся от высказывания после того, как мы убрали всё его конкретное содержание. Именно концентрация на логических формах высказываний и логических отношениях между ними делает логику универсальной, применимой к любому рассуждению, независимо от его предмета.

Выявление логических форм так важно, потому что оно способно дать нам полезную информацию о рассуждении, даже если мы не разбираемся в теме. Только по форме высказываний можно определить, корректно ли рассуждение, правильно ли дано определение, правильно ли используются понятия, не пытаются ли нас намеренно запутать и т.д. Поэтому главная задача этого урока – научиться отвлекаться от содержания высказываний и выявлять их логические формы.

Содержание

Видео:Максудова-Елисеева Г.В. Невиданные безумцы Готтлоба ФрегеСкачать

Язык как система знаков

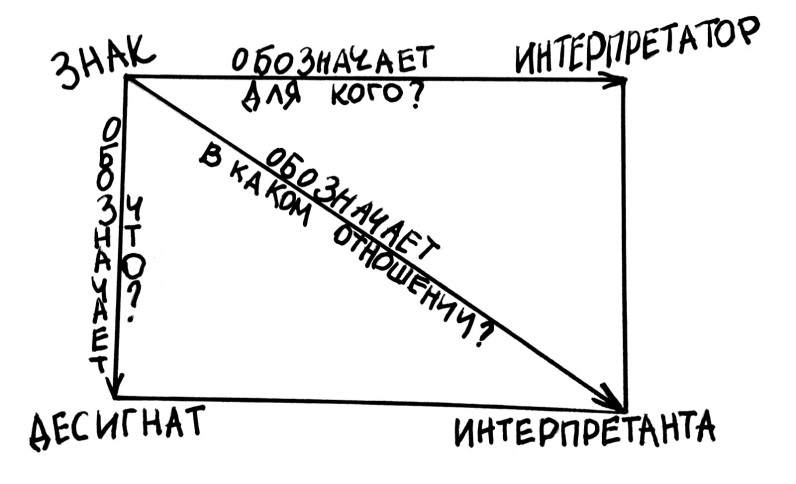
Чтобы научиться этому, сначала необходимо понять, что для логиков представляет собой язык. Начнём с того, что они видят в языке, прежде всего, знаковую систему. Буквы, слова, предложения – всё это знаки. Согласно знаменитому определению основоположника науки о знаках – семиотики – Чарльза Пирса, знак – «это нечто, что обозначает что-либо для кого-нибудь в определенном отношении или объеме» (Пирс Ч.С. Избранные философские произведения, М.: Логос, 2000, с. 177). Это довольно запутанное определение можно представить в виде квадрата:

В естественном языке знаками будут слова, словосочетания и предложения. «Авокадо», «тренер сборной Германии по футболу», «Александр Сергеевич Пушкин», «Кошки много спят» – всё это знаки. Я пишу их в кавычках специально, чтобы показать, что речь идёт именно о знаках – сочетаниях букв и звуков, которые нечто для нас обозначают. То, что знак обозначает, называется десигнатом. Десигнатами могут быть предметы, люди, абстрактные сущности, состояния, ситуации, положения дел в мире – в общем, всё что угодно. Слово «апельсин» обозначает для меня конкретный предмет. Слово «Иван» – конкретного человека. Предложение «Сегодня выпал снег» – положение дел. Интерпретатор – это человек, который воспринимает нечто (в случае языка – письменные символы и звуковые сочетания) как знак чего-то. Интерпретанта – это то, как человек реагирует на знак (например, если я вижу на перекрёстке знак «Стоп», то я останавливаю свою машину).

Отношение знаков к десигнатам описывается семантикой. Отношения знаков между собой – синтактикой. Отношение знаков к интерпретатору и интерпретанте – прагматикой. Логика не занимается прагматикой, так как последняя всегда связана с конкретной ситуацией, от которой логика стремится абстрагироваться. Зато изучение семантики и синтактики становятся её важными разделами.

Далее, язык состоит не просто из знаков, но знаков определённого рода – знаков-символов. Знаки-символы связаны со своими десигнатами произвольным образом. Например, буквы произвольным образом связаны со звуками (и это хорошо видно из наличия разных алфавитов), слова произвольно связаны с обозначаемыми предметами и явлениями (по-русски мы говорим «собака», по-английски – «dog», по-французски – «chien»; выбранное слово произвольно и ничего не говорит нам о животном, которое мы так называем), предложения произвольно связаны с выражаемыми мыслями (одну и ту же мысль можно передать с помощью совершенно разных предложений).

Кроме того, помимо знаков-символов есть и другие. Например, если знак копирует объект, это иконический знак 🐶. Иконические знаки также называют знаками-копиями и знаками-изображениями. А если знак указывает на объект, это индексальный знак или просто знак-признак (вспомните значок фирмы Nike или Adidas). Когда же знак символизирует объект, находясь в условной связи с ним, это уже знак-символ (как в примере со словами «собака», «dog» и т.д.)

Каждый тип знака обладает своими преимуществами, способными создать максимальный эффект. Те же иконические знаки и знаки-символы очень легко воспринимаются и создают в сознании наблюдателя конкертный образ и позволяют соотнести его с изначальным объектом без каких-либо усилий.

Видео:Философия XX века. Истоки современных течений. Континентальная и аналитическая. Часть I [Нарратив#5]Скачать

Треугольник Фреге

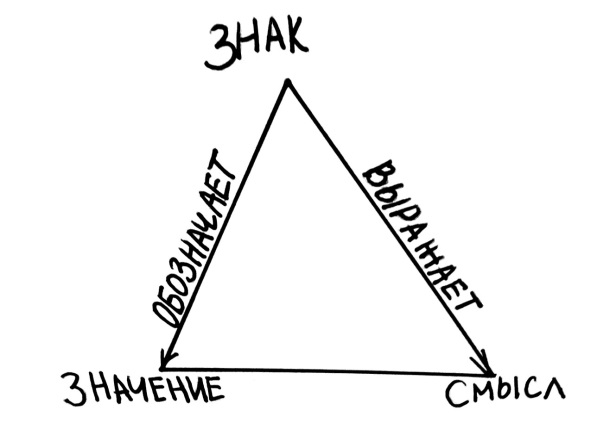
Один из основоположников современной логики Готлоб Фреге заметил, что знаки обладают определённой двойственностью. С одной стороны, они обозначают какие-то объекты, а с другой – передают интерпретатору некоторую дополнительную информацию о них. Например, возьмём словосочетание «автор “Войны и мира”». Это знак, обозначающий Льва Толстого. Помимо того, что этот знак указывает на конкретного человека, он также сообщает нам, что этот человек написал определённую книгу. Фреге назвал значением тот объект, который знак обозначает, и смыслом – ту дополнительную информацию, которую он несёт. Так появился треугольник Фреге:

Интересно отметить, далеко не все знаки обладают этими двумя характеристиками. Например, знак «нынешний король Франции» не имеет никакого значения, так как он обозначает несуществующий предмет, зато обладает смыслом. В то же время какой-нибудь знак «а» может обладать значением, которое я хочу ему придать, но не выражает никакого смысла. Помимо этого, различение значения и смысла понятно, когда речь идёт о словах и словосочетаниях. Но как быть с предложениями? Логики считают, что повествовательные предложения тоже обладают значением и смыслом. Поскольку они утверждают нечто о мире, то их значением будет «истина» либо «ложь», а смыслом – собственно описанная ими ситуация. Допустим, дано предложение: «Павлов открыл и описал действие условных рефлексов». Значение этого предложения – «истина». Смысл – тот факт, что Павлов открыл и описал действие условных рефлексов. При этом предложения, как и слова, могут не иметь значения. Например, возьмём предложение «Все дети Джона лысы». По идее, оно должно быть либо истинным, либо ложным. Однако что если у Джона нет детей? В таком случае мы не можем приписать ему никакого значения.

Поскольку знаки произвольны, то для удобства при анализе мы можем заменять их более простыми символами. Они будут иметь то же значение, но будут абстрагироваться от смысла. Соответственно, выражения языка будут рассматриваться в зависимости не от их содержания, а от той семантической функции, которую они выполняют. Выявление семантических функций и замена выражений простыми символами – очень важная процедура, так как по большому счёту она и представляет собой процесс отвлечения от содержания высказываний и переход на уровень логических форм.

Игра на эффект Cтрупа

Чтобы вы смогли понять, насколько иногда нам сложно отделять знак, его значение и смысл, предлагаем сыграть в игру по мотивам эффекта Струпа.

В психологии эффектом Струпа (англ. Stroop effect) называют задержку реакции при прочтении слов, когда цвет слов не совпадает с написанными словами (к примеру, слово «красный» написано синим). Эффект назван в честь Джона Ридли Струпа, впервые опубликовавшего этот тест на английском в 1935 году. До этого этот эффект был опубликован в Германии в 1929 году. Это исследование стало одним из наиболее цитируемых исследований в истории экспериментальной психологии.

Сейчас мы вам предлагаем пройти нашу модификацию данного теста.

Напоминаем, что для полноценной работы сайта вам необходимо включить cookies, javascript и iframe. Если вы ввидите это сообщение в течение долгого времени, значит настройки вашего браузера не позволяют нашему порталу полноценно работать.

Видео:К вопросу о политических взглядах Готтлоба ФрегеСкачать

Виды языковых выражений

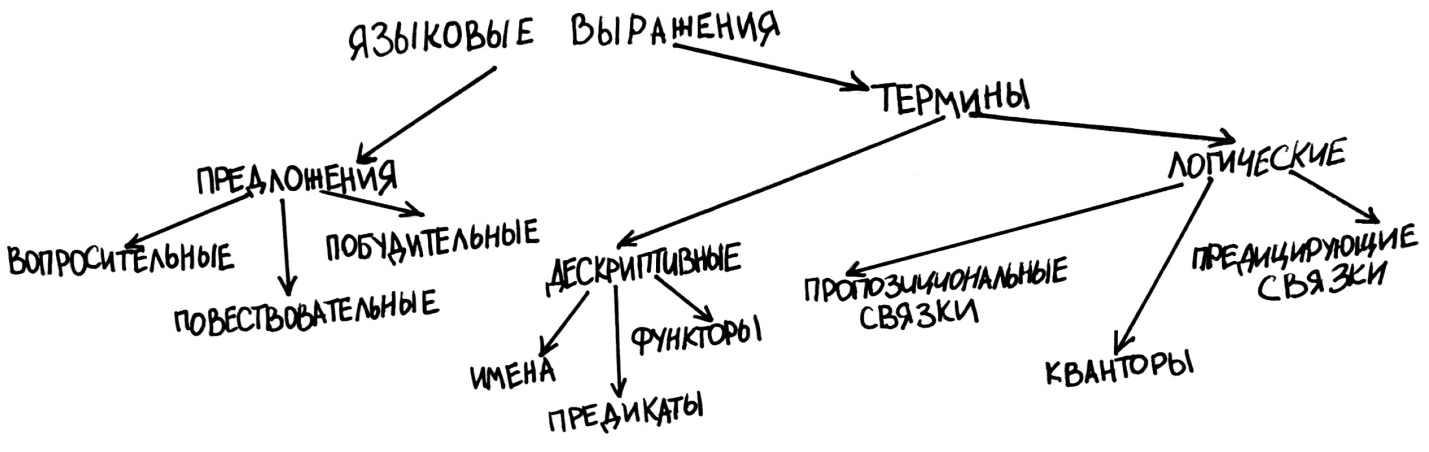
В зависимости от выполняемых ими семантических функций языковые выражения делятся на следующие виды:

Расшифруем, что это всё обозначает. Итак, языковые выражения делятся на два типа: предложения и термины.

Предложение – это знаковая форма для передачи мыслей. Если мысль представляет собой вопрос, то она выражается вопросительным предложением. Если мы имеем дело с императивом, то – побудительным предложением. Если же речь идёт о суждении, то есть мысли об утверждении или отрицании наличия некоторой ситуации в мире, то его выражают с помощью повествовательных предложений. Стоит отметить, что логика в основном концентрируется на изучении как раз повествовательных предложений, так как они выступают главным способом передачи знания о мире. Мы в этом курсе также будем говорить по большей части именно о них.

Термины – это значимые части предложений или, если говорить проще, слова и словосочетания. Они в свою очередь делятся на термины логические, то есть термины, которые что-то говорят о логическом устройстве предложений, и термины дескриптивные, то есть термины, которые что-то описывают, несут какую-то информацию о положении дел в мире. Дескриптивные термины различаются в зависимости от того, что именно они обозначают. Имена обозначают какой-то один единственный объект. Например, «Елизавета II» обозначает ровно одного человека. При этом именем может быть и словосочетание: «нынешняя королева Великобритании» тоже обозначает ровно одного человека. Предикаты обозначают свойства, состояния, отношения: «быть красным», «быть английской королевой», «граничить с», «знать иностранный язык» и т.д. В естественном языке предикатам соответствуют нарицательные существительные, прилагательные, глаголы. Функторы обозначают качественные и количественные характеристики предметов. К ним относятся знаки математических операций, физические величины и т.п.: «корень из», «натуральный логарифм от», «масса», «скорость».

Логические термины – это то, на что, прежде всего, обращает внимание логик, сталкиваясь с какими-то рассуждениями. В этом курсе мы тоже попытаемся научиться видеть их и использовать это умение. Итак, логические термины делятся на предицирующие связки, пропозициональные связки и кванторы. Предицирующие связки – это связки «есть» и «не есть». В естественном языке они могут выражаться разными словами («являться», «выступать» и т.д.) или даже опускаться («Сократ – человек»). Пропозициональные связки выражают отношения между различными предложениями или между компонентами одного предложения. К этим связкам относятся: «и», «или», «неверно, что», «если…, то», «если и только если». Кванторы передают информацию о количестве предметов. Квантор общности выражается словами «все», «ни один», «каждый», «любой». Квантор существования передаётся словами «существует», «некоторые», «большинство», «какой-нибудь».

Видео:Uebermarginal поясняет на примере Sense and reference Фреге. Ueber marginal. Убермаргинал.Скачать

Примеры логического анализа предложений

Посмотрим, как вся эта теория работает на практике. Возьмём несколько предложений и рассмотрим их компоненты с точки зрения семантических функций.

Начнём с предложения: « Катя пошла в кино, а Люда осталась дома зубрить сопромат». Во-первых, это сложное предложение состоит из двух простых: « Катя пошла в кино», « Люда осталась дома зубрить сопромат». Между собой они соединяются союзом « а», который в логике приравнивается к пропозициональной связке « и». То есть мы получаем два повествовательных предложения, связанных пропозициональной связкой « и». Для удобства мы можем заменить наши простые предложения знаками « р» и « q», тогда логическая форма этого предложения будет выглядеть следующим образом: « р и q».

Теперь посмотрим на предложение: « Петя пошёл на занятия или прогулял их». Хотя это предложение простое, в логике оно будет разбиваться на две части: « Петя пошёл на занятия» и « Петя прогулял занятия», соединённые пропозициональной связкой « или». К тому же предложение « Петя прогулял занятия» эквивалентно предложению « Петя не пошёл на занятия» или « Неверно, что Петя пошёл на занятия». Таким образом, наше предложение будет выглядеть для логика так: « Петя пошёл на занятия, или неверно, что Петя пошёл на занятия». Заменяем предложения на простые знаки и получаем логическую форму: « р или неверно, что р». Кстати, предложения такой формы всегда истинны. Логическая форма предложения « Если бросить камень в окно, то оно разобьётся» – « если р, то q». Логическая форма предложения « Я выйду за тебя, если и только если ты подаришь мне кольцо с брильянтом» – « р, если и только если q». И так далее.

Вы, наверное, уже обратили внимание, что сейчас мы только выделяли простые предложения и пропозициональные связки между ними, но не затрагивали другие термины внутри предложений. Примерно в таком духе работает логика высказываний. В её рамках простые предложения заменяются короткими символами « p», « q», « r», « s» и т.д. и выявляются те пропозициональные связки, которые соединяют их между собой (« и», « или», « неверно, что», « если, то»). В принципе даже такой поверхностный анализ может быть очень полезным, так как он помогает прояснить отношения между высказываниями в ходе рассуждения: выявлять парадоксы, тавтологии, противоречия и отсекать ложные высказывания, исходя только из их формы.

Безусловно, логический анализ может идти и глубже и затрагивать не только отношения между предложениями, но и отношения между логическими и нелогическими терминами внутри простых предложений. К логическим системам, которые основаны на таком более детальном анализе, относятся логика предикатов и силлогистика. Попробуем проанализировать несколько простых предложений, определяя семантические функции входящих в них терминов, чтобы получить представление, как они работают.

Возьмём предложение: « Все динозавры вымерли». « Все» – это квантор общности. « Динозавры» – это предикат, так как этот термин обозначает свойство « быть динозавром», которое присуще целому классу объектов. « Вымерли» – это тоже предикат, обозначающий свойство « быть вымершим». Чтобы записать логическую форму этого предложения, мы можем заменить предикаты буквами S и P. Попробуем: « Все S P». Получилось что-то странное и не имеющее особого смысла. Проблема в том, что мы пропустили предицирующую связку « есть». Хотя в естественном языке в этом предложении слова « есть» нет и не может быть, с точки зрения логики предицирующая связка « есть» здесь присутствует. Она связывает между собой два предиката: « быть динозавром» и « быть вымершим». В итоге мы получаем: « Все S есть P».

Теперь возьмём предложение: « Некоторые дети часто плачут, но Аня – плачет редко». В этом предложении две части. Начнём с первой. « Некоторые» – это квантор существования, то есть он как бы говорит нам: « Существуют такие объекты, которым присуще быть детьми и часто плакать». « Дети» и « часто плакать» – предикаты, не забываем о невидимой предицирующей связке « есть». Получаем: « Некоторые S есть P». Перейдём ко второй части. « Аня» – это имя, оно обозначает одного-единственного конкретного человека. « Плакать редко» эквивалентно « не плакать часто». Это значит, что мы имеем здесь тот же предикат, что и в первой части – « плакать часто» и предицирующую связку « не есть». Логическая форма этого предложения: « а не есть P». Союз « но» представляет собой пропозициональную связку « и». В итоге: « Некоторые S есть P, и а не есть P».

Таким образом и происходит логический анализ языковых выражений. Сначала определяются семантические функции предложений и слов, затем предложения, имена, предикаты и функторы заменяются короткими удобными символами, которые позволяют отвлечься от конкретного содержания, и выявляются те логические термины, которые связывают их между собой. Это даёт нам возможность проверить, насколько данное рассуждение корректно с точки зрения его логической формы. Естественно, чем более детальный логический анализ языка проводится, тем более сложной будет логическая система. Но одновременно и тем более тонким инструментом для разбора рассуждений она окажется. Конечно, примеры анализа, приведённые выше, могут показаться сложными и не до конца ясными. В этом нет ничего страшного: когда мы перейдём к конкретным темам, их значение прояснится. На сегодня важно запомнить, что за словами естественного языка нужно научиться видеть их семантические функции, за предложениями – их логические формы. Это станет ключом к умению логично рассуждать.

Напоследок, предлагаем вам несколько несложных логических задач. Попробуйте представить их решение в виде пошагового рассуждения. Где это возможно, абстрагируйтесь от содержания предложений и перейдите на уровень логических форм.

Видео:Бертран Рассел. Логический Атомизм.Скачать

Упражнения

«Живописная» экспертиза (Из книги Сергея Быльцова «Логические головоломки и задачи»)

Одному коллекционеру принесли картину, якобы принадлежащую перу кисти Антонио Канале, прозванному Каналетто. Коллекционер не был большим знатоком живописи и потому пригласил на экспертизу трёх специалистов. Эксперты высказали о картине следующие суждения:

• Первый: Это не только не Каналетто, но даже и не Гварди.
• Второй: Это не Каналетто, но это настоящий Алессандро Маньяско.
• Третий: Конечно, это не Маньяско, это, несомненно, Антонио Канале.

Впоследствии объективными методами авторство картины было установлено, и оказалось, что один из экспертов сказал правду, другой ошибся, а третий был прав наполовину. Кто автор картины?

Принцесса и Иванушка

В этом упражнении вам необходимо найти принцессу, исходя из имеющихся данных на табличках. История такова: в поисках принцессы, похищенной Кощеем, Иванушка оказался в старинном замке. Преодолев массу препятствий, он очутился в помещении, из которого вели три двери. Иванушка знал, что за какой-то из них находится принцесса, за другой сидит тигр, а за оставшейся дверью никого нет.

Напоминаем, что для полноценной работы сайта вам необходимо включить cookies, javascript и iframe. Если вы ввидите это сообщение в течение долгого времени, значит настройки вашего браузера не позволяют нашему порталу полноценно работать.

Предлагаем вам также пройти упражнение, которое отлично показывает, что наш мозг может находить и понимать смысл слов, даже если его пытаются намеренно запутать. Это происходит потому, что мы читаем не по буквам и слогам, а слова целиком и кроме того, смысл слов мы понимаем благодаря соседним словам и словосочетаниям, с которыми наш мозг сталкивался раньше.

Напоминаем, что для полноценной работы сайта вам необходимо включить cookies, javascript и iframe. Если вы ввидите это сообщение в течение долгого времени, значит настройки вашего браузера не позволяют нашему порталу полноценно работать.

Видео:7 2 Теории знакаСкачать

Проверьте свои знания

Если вы хотите проверить свои знания по теме данного урока, можете пройти небольшой тест, состоящий из нескольких вопросов. В каждом вопросе правильным может быть только 1 вариант. После выбора вами одного из вариантов, система автоматически переходит к следующему вопросу. На получаемые вами баллы влияет правильность ваших ответов и затраченное на прохождение время. Обратите внимание, что вопросы каждый раз разные, а варианты перемешиваются.

Напоминаем, что для полноценной работы сайта вам необходимо включить cookies, javascript и iframe. Если вы ввидите это сообщение в течение долгого времени, значит настройки вашего браузера не позволяют нашему порталу полноценно работать.

📽️ Видео

Философия Готлаба Фреге и основа аналитической философии.Скачать

Вопрос 17. Логический позитивизм (неопозитивизм) и проблема демаркации научного знания.Скачать