Гипотенуза прямоугольного треугольника меньше катета

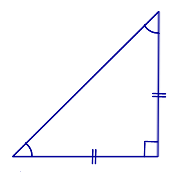Определение равнобедренного прямоугольного треугольника:

Равнобедренным прямоугольным треугольником называют такой прямоугольный треугольник, у которого равны катеты.

Свойство углов прямоугольного треугольника:

Острые углы равнобедренного прямоугольного треугольника равны 45° .

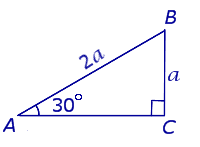Свойство прямоугольного треугольника с углом в 30° :

Катет прямоугольного треугольника, лежащий против угла в 30° , равен половине гипотенузы.

Признак прямоугольного треугольника с углом в 30° :

Если в прямоугольном треугольнике один из катетов равен половине гипотенузы, то этот катет лежит против угла в 30° .

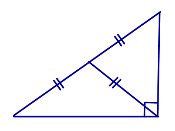Свойство медианы, проведенной к гипотенузе прямоугольного треугольника:

Медиана прямоугольного треугольника, проведённая из вершины прямого угла, равна половине гипотенузы.

Признак прямоугольного треугольника:

Если в треугольнике медиана равна половине стороны, к которой она проведена, то такой треугольник является прямоугольным.

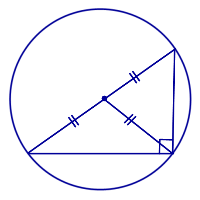Свойство окружности, описанной около прямоугольного треугольника:

Середина гипотенузы прямоугольного треугольника является центром описанной около него окружности.

Признак прямоугольного треугольника:

Если в треугольнике центр описанной окружности лежит на одной из сторон, то этот треугольник является прямоугольным треугольником, а центр описанной окружности совпадает с серединой гипотенузы.

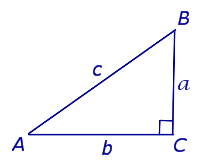В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов

Обратная теорема Пифагора:

Если в треугольнике квадрат одной стороны равен сумме квадратов двух других сторон, то такой треугольник является прямоугольным

Видео:Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать

Гипотенуза прямоугольного треугольника меньше катета

Какие из следующих утверждений верны?

1) Длина гипотенузы прямоугольного треугольника меньше суммы длин его катетов.

2) В тупоугольном треугольнике все углы тупые.

3) Средняя линия трапеции равна полусумме её оснований.

Если утверждений несколько, запишите их номера в порядке возрастания.

Проверим каждое из утверждений.

1) «Длина гипотенузы прямоугольного треугольника меньше суммы длин его катетов» — верно, для того, чтобы существовал треугольник, сумма любых его двух сторон должна быть больше третьей стороны.

2) «В тупоугольном треугольнике все углы тупые» — неверно: в тупоугольном треугольнике один тупой и два острых угла.

3) «Средняя линия трапеции равна полусумме её оснований» — верно.

Видео:Длина гипотенузы прямоугольного треугольника ... | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

Гипотенуза прямоугольного треугольника меньше катета

Задание 20. Какие из следующих утверждений верны?

1) Длина гипотенузы прямоугольного треугольника меньше суммы длин его катетов.

2) Если точка лежит на биссектрисе угла, то она равноудалена от сторон этого угла.

3) Если диагонали параллелограмма равны, то он является ромбом.

1) Верно. Длина гипотенузы всегда меньше сумм катетов прямоугольного треугольника.

2) Верно. Так как биссектриса делит угол пополам, то расстояние от нее до противоположных сторон угла будет одинаковым.

3) Не верно. Диагонали у ромба должны пересекаться под прямым углом и не обязательно быть равными. Если в параллелограмме диагонали равны это еще не означает, что они пересекаются под прямым углом.

📽️ Видео

Катеты и гипотенузаСкачать

Найди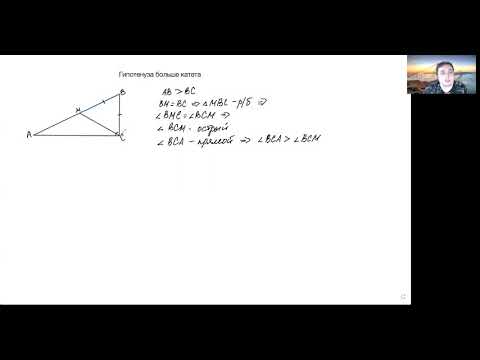те площадь прямоугольного треугольника, если сумма его катетов равна 15, а гипотенуза равна 13Скачать

Определение длины гипотенузыСкачать

№256. Один из углов прямоугольного треугольника равен 60°, а сумма гипотенузы и меньшего из катетовСкачать

7 кл г. Теорема: «катет лежавший напротив угла в 30 градусов равен половине гипотенузы»Скачать

Задача по геометрии на прямоугольный треугольник и теорему Пифагора из реального ОГЭ по математикеСкачать

Как найти гипотенузу в прямоугольном треугольнике, минуя теорему Пифагора?Скачать

Теорема Пифагора для чайников)))Скачать

Свойства прямоугольного треугольника. 7 класс.Скачать

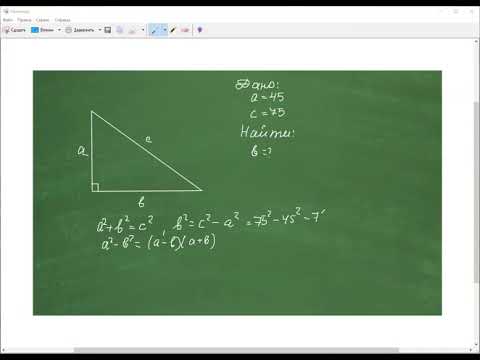Найдите углы прямоугольного треугольника, если его гипотенуза равна 12, а площадь равна 18Скачать

КАТЕТЫ И ВЫСОТА В ПРЯМОУГОЛЬНОМ ТРЕУГОЛЬНИКЕ ЧАСТЬ I #математика #егэ #огэ #Shorts #геометрияСкачать

Геометрия 7 класс (Урок№25 - Прямоугольные треугольники.)Скачать

Катеты прямоугольного треугольника равны 3 и 4. Найдите высоту, проведённую к гипотенузеСкачать

Лайфхак нахождения катета в прямоугольном треугольникеСкачать

Доказать, что сумма кубов катетов меньше куба гипотенузыСкачать

7 класс, 35 урок, Некоторые свойства прямоугольных треугольниковСкачать

Математика | Соотношения между сторонами и углами в прямоугольном треугольнике.Скачать