Геометрия 8 класс таблица 20 касательная к окружности гдз (5 видео)

Геометрия. 8 класс. Решебник к книге «Геометрия. Задачи на готовых чертежах.» Балаян Э.Н.

Р. на Д.: 20 1 9. — 1 92 с.

В предлагаемом пособии приводятся полные решения всех без исключения задач для 8-го класса из книги «Геометрия: задачи на готовых чертежах для подготовки к ОГЭ и ЕГЭ: 7-9 классы». Некоторые задачи решены различными способами, чтобы читатель имел возможность ознакомиться с сущностью рационального решения. Ученикам будет целесообразно обращаться к «решебнику» уже после того, как они самостоятельно решат задачи, или же тогда, когда они убедятся в том, что не в силах самостоятельно справиться с заданием. Кроме того, приводятся краткие теоретические сведения по курсу геометрии 7-9 классов, сопровождаемые определениями, теоремами, основными свойствами и необходимыми справочными материалами. Пособие адресовано учащимся общеобразовательных школ, лицеев, колледжей, а также начинающим учителям математики, студентам — будущим учителям и репетиторам.

СОДЕРЖАНИЕ
К таблице 1. Определение и признаки параллелограмма 3
К таблице 2. Свойства параллелограмма 6
К таблице 3. Свойства параллелограмма 13
К таблице 4. Параллелограмм 19
К таблице 5. Параллелограмм 21
К таблице 6. Трапеция 24
К таблице 7. Трапеция 28
К таблице 8. Площадь прямоугольника 31
К таблице 9. Площадь параллелограмма 35
К таблице 10. Площадь треугольника 42
К таблице 11. Площадь трапеции 50
К таблице 12. Теорема Пифагора 58
К таблице 13. Определение подобных треугольников 75
К таблице 14. Признаки подобия треугольников 84
К таблице 15. Признаки подобия треугольников 90
К таблице 16. Средняя линия треугольника 93
К таблице 17. Пропорциональные отрезки в прямоугольном треугольнике 97
К таблице 18. Соотношения между сторонами и углами в прямоугольном треугольнике 102
К таблице 19. Соотношения между сторонами и углами в прямоугольном треугольнике 105
К таблице 20. Касательная к окружности 112
К таблице 21. Центральные и вписанные углы 116
К таблице 22. Четыре замечательные точки треугольника 125
К таблице 23. Вписанная и описанная окружности 129
К таблице 24. Векторы 152
К таблице 25. Средняя линия трапеции 160
Краткие теоретические сведения 167
Планиметрия 167
1.Углы 167
2. Многоугольник 168
3. Правильные многоугольники 169
4. Треугольник 169
5. Признаки равенства треугольников 171
6. Неравенства треугольника 172
7. Определение вида треугольника по его сторонам 172
8. Прямоугольные треугольники (некоторые свойства) 172
9. Признаки равенства прямоугольных треугольников 172
10. Четыре замечательные точки треугольника 173
11. Произвольный треугольник 174
12. Теорема Чевы 175
13. Теорема Менелая 175
14. Теорема синусов 176
15. Теорема косинусов 176
16. Площадь треугольника 176
17. Равносторонний (правильный) треугольник 176
18. Подобные треугольники 177
19. Признаки подобия треугольников 177
20. Четырехугольник 178
21. Параллелограмм 178
22. Трапеция 179
23. Прямоугольник 180
24. Ромб 181
25. Квадрат 181
26. Окружность 181
27. Свойства касательных к окружности 182
28. Окружность и треугольник 182
29. Окружность и четырехугольник 183
30. Углы и окружность 183
31. Метрические соотношения в окружности 185
32. Длина окружности. Площадь круга и его частей 185
33. Понятие вектора 186
34. Равенство векторов 186
35. Координаты вектора 186
36. Действия над векторами 187
37. Скалярное произведение векторов 187
38. Скалярное произведение в координатах 188
39. Свойства скалярного произведения векторов 188
40. Уравнение окружности 188
41. Уравнение прямой 188

О том, как читать книги в форматах pdf , djvu — см. раздел » Программы; архиваторы; форматы pdf, djvu и др. «

Содержание

Касательная к окружности. Решение задач
Просмотр содержимого документа «Касательная к окружности. Решение задач»
Урок геометрии в 8-м классе «Касательная к окружности»
🎬 Видео

Видео:8 класс, 32 урок, Касательная к окружностиСкачать

Касательная к окружности. Решение задач

Просмотр содержимого документа
«Касательная к окружности. Решение задач»

8 класс. Геометрия

Решение задач по теме «Касательная к окружности»

Учитель математики: Барсукова И.Е.

Повторение теоретического материала

Как вы думаете, сколько общих точек могут иметь прямая и окружность?

r две общие точки одна общая точка не имеют общих точек Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая и окружность имеют только одну общую точку . Если расстояние от центра окружности до прямой меньше радиуса окружности, то прямая и окружность имеют две общие точки . Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общих точек . » width=»640″

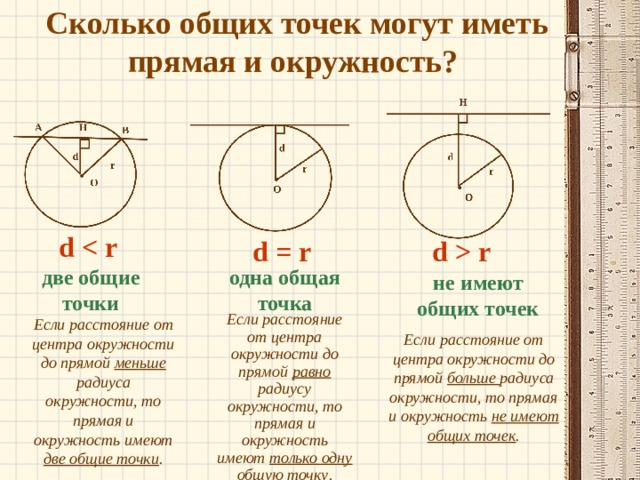
Сколько общих точек могут иметь прямая и окружность?

две общие точки

одна общая точка

не имеют общих точек

Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая и окружность имеют только одну общую точку .

Если расстояние от центра окружности до прямой меньше радиуса окружности, то прямая и окружность имеют две общие точки .

Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общих точек .

Касательная к окружности

Определение: П рямая, имеющая с окружностью только одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности.

Свойство касательной: Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.

m – касательная к окружности с центром О

М – точка касания

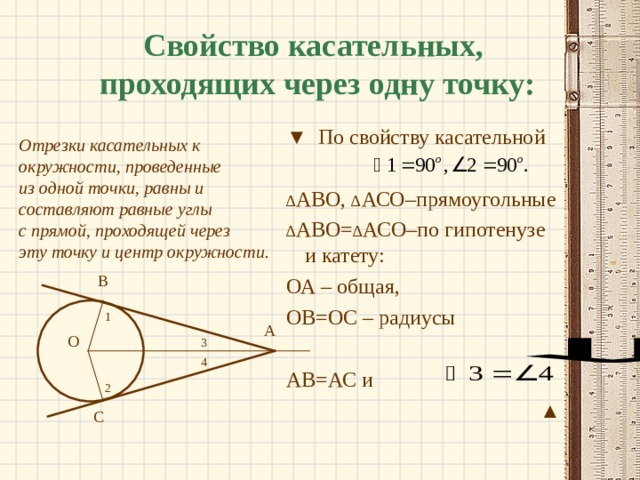
Свойство касательных, проходящих через одну точку:

Отрезки касательных к

из одной точки, равны и

составляют равные углы

с прямой, проходящей через

эту точку и центр окружности.

▼ По свойству касательной

∆ АВО= ∆ АСО–по гипотенузе и катету:

Признак касательной: Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна радиусу, то она является к асательной.

окружность с центром О

m – прямая, которая проходит через точку М

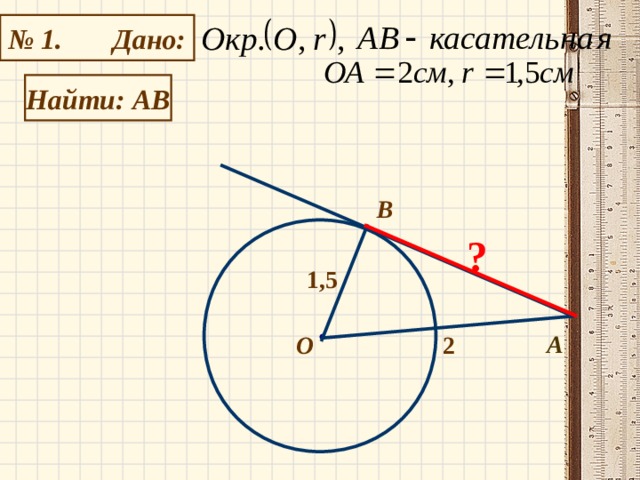
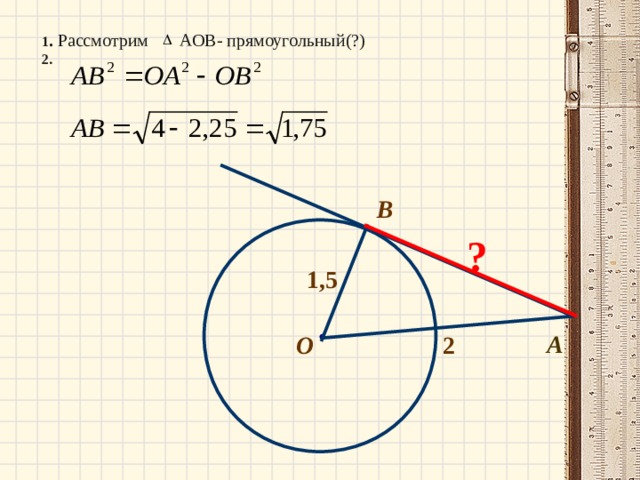
1 . Рассмотрим АОВ- прямоугольный(?)

Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Урок геометрии в 8-м классе «Касательная к окружности»

Разделы: Математика

Цели:

ввести понятие касательной, точки касания,
рассмотреть свойство касательной и её признак и показать их применение при решении задач в природе и технике.

Образовательные:

Обеспечить овладение основными алгоритмическими приёмами построения касательной к окружности,
Сформировать умения применять теоретические знания к решению задач.

Воспитательные:

Развивать мышление и речь учащихся,
Работать над формированием умений наблюдать, подмечать закономерности, обобщать, проводить рассуждения по аналогии,
Привитие интереса к математике.

Практические: сформировать умение строить касательную к окружности, рассмотреть примеры в природе и технике.

Тип урока: комбинированный.

Оборудование:

Карточки с заданиями,
Циркуль, треугольник, линейка
Мультимедийный проектор, слайды,
Модель “Дуб и кот”, маркер.

Оформление кабинета:

Рисунки детей “У лукоморья дуб зелёный…”
Плакат с высказыванием Козьмы Пруткова

“Наука изощряет ум; ученье вострит память”

I. Организационный момент. (1мин.)

Постановка целей урока.

Ребята этот урок мы посвятим изучению свойства касательной к окружности, научимся строить её. Рассмотрим применение касательной для построения кривых.

II. Повторение изученного материала. (4минут)

1) У каждого ученика карточка с копиркой.

Учащиеся сдают листочки с ответами.

Учитель зачитывает предложение полностью, ученик у которого ответ неверный ставит “минус”, верный – “плюс”.

III. Подготовка к восприятию нового материала. (5минут)

В тетради начертить окружность произвольного радиуса с центром в точке О, провести три прямые, так чтобы получилось разное количество общих точек у прямой и окружности.

Один ученик выполняет задание у доски.

Геометрия 8 класс таблица 20 касательная к окружности гдз

Обозначим прямые и полученные точки:

d r нет общих точек

d=r 1 общая точка

IV. Объяснение нового материала. (7минут)

На этом уроке мы рассмотрим свойства окружности и прямой c.

1. Работа с учебником.

На страница 159 найти и прочитать определение касательной к окружности.

Определение. Прямая, имеющая с окружностью только одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности.

Назвать на рисунке точку касания и прямую касательную к окружности.

(C— точка касания, прямая с – касательная к окружности)

Какими же свойствами обладает эта прямая? Чтобы ответить на этот вопрос —

проведите отрезок соединяющий центр окружности и точку касания, измерьте получившийся угол. (90)

— Что можно сказать о касательной и радиусе? — Они перпендикулярны.

2. Прочтите теорему.

Касательная к окружности перпендикулярна к радиусу, проведённому в точку касания.

Доказательство разбирается в ходе беседы.

Учащиеся делают новый чертёж.

Допустим, что прямая р не перпендикулярна к радиусу ОА(На рисунке сделать построение другим цветом). Сравните расстояние от центра окружности до прямой р с радиусом окружности.

Назовите перпендикуляр к прямой р ОВ

-Расстояние от точки О до прямой р , это ОВ, меньше радиуса окружности ОА, который в данном случае будет являться наклонной по отношению к прямой р, а расстояние от точки О до прямой р – перпендикуляр, а, как известно, любая наклонная больше перпендикуляра, проведённого из той же точки к той же прямой, т. е. ОВ (2минуты)

Глубоко вдохните, зажмурив глаза как можно сильнее. Напрягите мышцы шеи, лица, головы. Задержите дыхание на 2-3 секунды, потом быстро выдохните, широко раскрыв на выдохе глаза. Повторить 5 раз.
Закройте глаза, помассируйте надбровные дуги и нижние части глазниц круговыми движениями — от носа к вискам.
Закройте глаза, расслабьте брови. Повращайте глазными яблоками слева направо и справа налево. Повторить 10 раз.
Поставьте большой палец руки на расстоянии 25-30 см. от глаз, смотрите двумя глазами на конец пальца 3-5 секунд, закройте один глаз на 3-5 секунд, затем снова смотрите двумя глазами, закройте другой глаз. Повторить 10 раз.
Положите кончики пальцев на виски, слегка сжав их. 10 раз быстро и легко моргните. Закройте глаза и отдохните, сделав 2-3 глубоких вдоха. Повторить 3 раза.

3. Построение касательной. (4 минуты)

Ученик, подготовленный заранее, объясняет построение касательной к окружности в заданной точке. Учащиеся выполняют построение в тетради.

Дано: окружность, О — центр, А — лежит на окружности.

Построить касательную к окружности в точке А.

Построение:

ОА – прямая.
От точки А отложим ОА=ОА.
Из точек О и О проведём окружности, радиусом большим ОА.
Через точки пересечения окружностей проведём прямую а.

Прямая а будет касательной по определению.

4. Построение эвольвенты. (10 минут)

Ученик читает отрывок из “Руслана и Людмилы”

У Лукоморья дуб зелёный
Златая цепь на дубе том.
И днём и ночью кот учёный
Всё ходит по цепи кругом.

Нам эти строки знакомы с детства, мы никогда не задумывались над тем, какую линию вычерчивает кот.

Как вы думаете, что это за линия? (Чаще всего ученики отвечают – окружность)

Два ученика, выходят к столу, на котором расположен ватман, макет дуба и небольшой котёнок (мягкая игрушка), к которому прикреплен маркер, привязанный к “дубу”.

Один ученик придерживает “дуб”, а второй передвигает игрушку “по цепи кругом”. На ватмане вычерчивается кривая.

Учитель показывает слайды построения эвольвенты. Приложение №2. Слайд 3.

Таким образом для построения этой кривой надо хорошо уметь строить касательную в заданной точке.

Ученикам раздаются карточки на которых написан порядок построения эвольвенты. Приложение №1.

После выполнения построения — лучшие работы оцениваются.

С этой же кривой связана и биология . (2 минуты)

1. Ученик рассказывает о берёзовом долгоносике, демонстрируя разрез листа и сворачивает его.

2. Ученик рассказывает о практическом применение касательной к окружности.

КОВШОВАЯ ГИДРОТУРБИНА (ПЕЛТОНА ТУРБИНА)

Гидротурбина, у которой вода (пар) на лопасти (ковши) рабочего колеса поступает через сопла по касательной к окружности, проходящей через середину ковша. Применяют при напорах св. 500 м. Мощность до 110 МВт. Патент на ковшовую гидротурбину в 1889 получил американский инженер А. Пелтон.

VI. Подведение итогов.

Оценки выставляются с учётом диктанта, активности на уроке, за построение эвольвенты. Рефлексия. Приложение №1.

VII. Домашнее задание.

П. 69, вопросы 1-4, №634, решить задачи по готовым чертежам, дополнительную задачу.

Литература:

Н. Ф. Гаврилова Поурочные разработки по геометрии 8 класс. Москва “ВАКО”, 2005.
А. Азевич. Кривые мудрого жучка.
Я. И. Перельман. Занимательная алгебра. “Тезис”, Екатеринбург, 1994
С. Акимова. Занимательная математика. Нескучный учебник. Тригон, С-Петербург,1997.