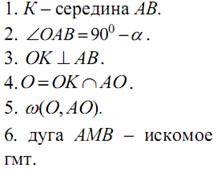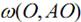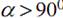Геометрическим местом точек называют множество точек, заданное условием, являющимся и свойством, и признаком.
Другими словами, все точки из рассматриваемого геометрического места точек, и только они, удовлетворяют заданному условию.
Примеры геометрических мест точек (сокращённо ГМТ ) на плоскости представлены в следующей таблице, причём геометрические места точек изображаются в таблице красным цветом .
Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Метод геометрических мест точек
Одним из методов решения задач на построение является метод геометрических мест. Понятие геометрического места является одним из важнейших в геометрии. Термин «геометрическое место точек» был введен еще древнегреческим ученым и философом Аристотелем (384-222 гг. до новой эры), который представлял себе линию, как некоторое «место», где могут быть размещены точки. Понятие линии как следа движущей точки или совокупность точек, возникли значительно позже.
Геометрическим местом точек (сокращенно ГМТ), обладающих определенным свойством, называется множество всех точек, которые обладают этим свойством.
Сущность метода состоит в следующем. Пусть, решая задачу на построение, нам надо найти точку X , удовлетворяющую двум условиям. ГМТ, удовлетворяющих первому условию, есть некоторая фигура A, а ГМТ, удовлетворяющих второму условию, есть некоторая фигура B. Искомая точка X принадлежит A и B, т.е. является их точкой пересечения.
При решении задач этим методом надо знать основные геометрические места точек на плоскости:
1. ГМТ, равноудаленных от двух данных точек.
2. ГМТ, находящихся на данном расстоянии oт данной точки.
3. ГМТ, удаленных на расстояние d oт данной прямой.
4. ГМТ, равноудаленных от двух данных параллельных прямых.
5. ГМТ, равноудаленных от сторон угла.
6. ГМТ, из которых данный отрезок виден под данным углом.
Некоторые геометрические места точек, часто используемые
Рассмотрим построение основных ГМТ, перечисленных в предыдущем пункте.
1. Геометрическим местом точек, равноудаленных от двух данных
точек, является серединный перпендикуляр к отрезку с концами в этих
2. Геометрическим местом точек, находящихся на данном расстоянии
oт данной точки, является окружность с центром в данной точке и радиусом, равном данному отрезку.
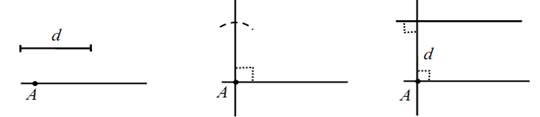
3. Геометрическим местом точек, удаленных на расстояние d oт
данной прямой в выбранной полуплоскости, является прямая
параллельная данной и находящаяся на расстоянии d от нее.
А выбираем произвольно.
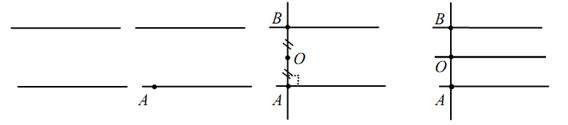
4. Геометрическим местом точек, равноудаленных от двух данных
параллельных прямых, является прямая, находящаяся на одинаковом
расстоянии от данных прямых (ось симметрии этих прямых).
5. Геометрическим местом точек, равноудаленных от сторон угла,
является биссектриса этого угла. (См. построение 4).
6. Геометрическим местом точек, из которых данный отрезок виден под
данным углом, является дуга окружности, опирающейся на этот отрезок.
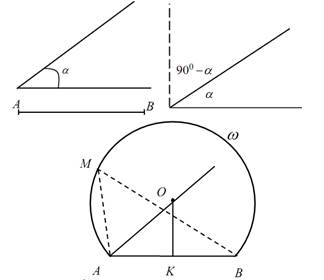
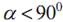
АВ – данный отрезок.
Действительно, ∟АМВ, как угол, вписанный в окружность, измеряется
половиной малой дуги АВ, так как центральный угол ∟АОВ = 2α, то
При этом заметим, что центр окружности О и вершина М угла лежат по
одну сторону от данного отрезка
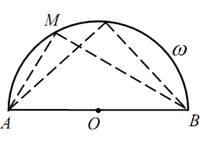
1. О – середина АВ.
Полуокружность
(Любой угол, опирающийся на диаметр –
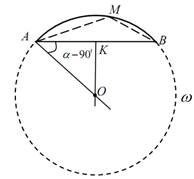
III случай:
Действительно, ∟АОВ = 2( 90 0 – (α — 90 0 )) = 2(180 0 — α). Тогда большая дуга
АВ равна 360 0 – 2(180 0 — α) = 2α и угол АМВ, опирающийся на большую дугу АВ, измеряется половиной этой дуги, т.е. равен α.
Видео:Геометрическое место точек окружность и круг - 7 класс геометрияСкачать

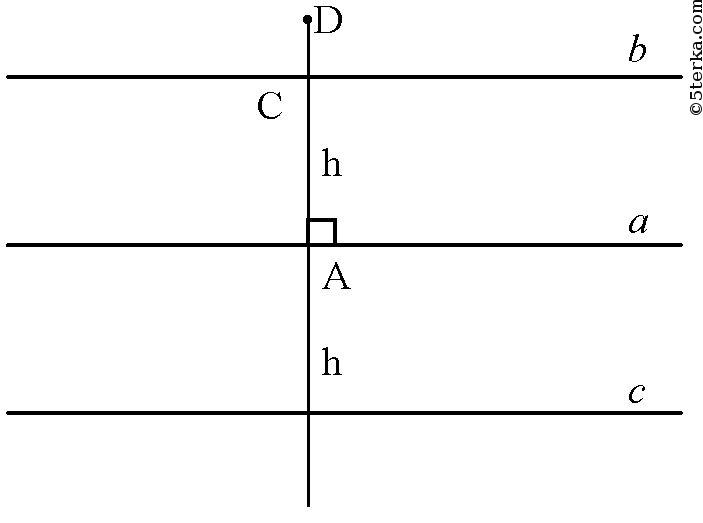
№ 41. Докажите, что геометрическое место точек, удаленных от данной прямой на расстояние h, состоит из двух прямых, параллельных данной и отстоящих от нее на h.
Т.к. расстояние от прямой до некоторой точки — это есть перпендикуляр к этой прямой через эту точку
Докажем, что любая точка, удаленная от а на h лежит либо на с, либо на b.
Пусть точка D не лежит ни на b, ни на с, и расстояние от D до точки А на прямой равно h.
Тогда DA = h и AD ⊥ a.
Но СА также равно h и СА ⊥ а.
Следовательно, точки С и D либо совпадают, либо противоположны относительно прямой а.
То есть точка D лежит на прямой b или на с.

задача №41
к главе «§ 5. Геометрические построения».
🌟 Видео
ГМТ // ГЕОМЕТРИЧЕСКОЕ МЕСТО ТОЧЕКСкачать

Геометрическое место точек (ГМТ).ОКРУЖНОСТЬ и КРУГ §19 геометрия 7 классСкачать

ГМТ РАВНОУДАЛЕННЫХ ОТ ДВУХ ПАР ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ. Задачи. Метод ГМТ. ГЕОМЕТРИЯ 7 классСкачать

ГЕОМЕТРИЧЕСКОЕ МЕСТО ТОЧЕК РАВНОУДАЛЕННЫХ ОТ СТОРОН УГЛА. Задачи на ГМТ | ГЕОМЕТРИЯ 7 классСкачать

ГЕОМЕТРИЧЕСКОЕ МЕСТО ТОЧЕК РАВНОУДАЛЕННЫХ ОТ КОНЦОВ ОТРЕЗКА. Задачи на ГМТ | ГЕОМЕТРИЯ 7 классСкачать

7 класс, 29 урок, Теоремы об углах, образованных двумя параллельными прямыми и секущейСкачать

7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

Найдите угол: задача по геометрииСкачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Видеоурок "Канонические уравнения прямой"Скачать

Удивительный способ решения сложной геометрической головоломкиСкачать

Геометрия 7 класс (Урок№33 - Повторение. Параллельные и перпендикулярные прямые.)Скачать

Геометрия 7 класс (Урок№26 - Расстояние от точки до прямой. Расстояние между параллельными прямыми.)Скачать

ГЕОМЕТРИЧЕСКОЕ МЕСТО ТОЧЕК РАВНОУДАЛЕННЫХ ОТ ТРЕХ ДАННЫХ ТОЧЕК. Задачи. Метод ГМТ. ГЕОМЕТРИЯ 7 классСкачать

Математика без Ху!ни. Уравнение плоскости.Скачать

Все типы 24 задание 2 часть ОГЭ ПО МАТЕМАТИКЕ 2023 УмскулСкачать

Уравнение параллельной прямойСкачать