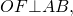Существование окружности, вписанной в треугольник. Основное свойство биссектрисы угла Существование окружности, вписанной в треугольник. Основное свойство биссектрисы угла |
 Формулы для радиуса окружности, вписанной в треугольник Формулы для радиуса окружности, вписанной в треугольник |
 Вывод формул для радиуса окружности, вписанной в треугольник Вывод формул для радиуса окружности, вписанной в треугольник |
- Существование окружности, вписанной в треугольник. Основное свойство биссектрисы угла
- Формулы для радиуса окружности, вписанной в треугольник
- Вывод формул для радиуса окружности, вписанной в треугольник
- Центр вписанной в треугольник окружности
- Где всегда находится центр вписанной окружности в треугольник
- 🎬 Видео
Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Существование окружности, вписанной в треугольник. Основное свойство биссектрисы угла
Определение 1 . Биссектрисой угла называют луч, делящий угол на две равные части.
Теорема 1 (Основное свойство биссектрисы угла) . Каждая точка биссектрисы угла находится на одном и том же расстоянии от сторон угла (рис.1).
Доказательство . Рассмотрим произвольную точку D , лежащую на биссектрисе угла BAC , и опустим из точки D перпендикуляры DE и DF на стороны угла (рис.1). Прямоугольные треугольники ADF и ADE равны, поскольку у них равны острые углы DAF и DAE , а гипотенуза AD – общая. Следовательно,
что и требовалось доказать.
Теорема 2 (обратная теорема к теореме 1) . Если некоторая точка находится на одном и том же расстоянии от сторон угла, то она лежит на биссектрисе угла (рис.2).
Доказательство . Рассмотрим произвольную точку D , лежащую внутри угла BAC и находящуюся на одном и том же расстоянии от сторон угла. Опустим из точки D перпендикуляры DE и DF на стороны угла (рис.2). Прямоугольные треугольники ADF и ADE равны, поскольку у них равны катеты DF и DE , а гипотенуза AD – общая. Следовательно,
что и требовалось доказать.
Определение 2 . Окружность называют окружностью, вписанной в угол , если она касается касается сторон этого угла.
Теорема 3 . Если окружность вписана в угол, то расстояния от вершины угла до точек касания окружности со сторонами угла равны.
Доказательство . Пусть точка D – центр окружности, вписанной в угол BAC , а точки E и F – точки касания окружности со сторонами угла (рис.3).
Прямоугольные треугольники ADF и ADE равны, поскольку у них равны катеты DF и DE (как радиусы окружности радиусы окружности ), а гипотенуза AD – общая. Следовательно
что и требовалось доказать.
Замечание . Теорему 3 можно сформулировать и по-другому: отрезки касательных касательных , проведенных к окружности из одной точки, равны.
Определение 3 . Биссектрисой треугольника называют отрезок, являющийся частью биссектрисы угла треугольника, и соединяющий вершину треугольника с точкой на противоположной стороне.
Теорема 4 . В любом треугольнике все три биссектрисы пересекаются в одной точке.
Доказательство . Рассмотрим две биссектрисы, проведённые из вершин A и C треугольника ABC , и обозначим точку их пересечения буквой O (рис. 4).
Опустим из точки O перпендикуляры OD , OE и OF на стороны треугольника. Поскольку точка O лежит на биссектрисе угла BAC , то в силу теоремы 1 справедливо равенство:
Поскольку точка O лежит на биссектрисе угла ACB , то в силу теоремы 1 справедливо равенство:
Следовательно, справедливо равенство:
откуда с помощью теоремы 2 заключаем, что точка O лежит на биссектрисе угла ABC . Таким образом, все три биссектрисы треугольника проходят через одну и ту же точку, что и требовалось доказать
Определение 4 . Окружностью, вписанной в треугольник , называют окружность, которая касается всех сторон треугольника (рис.5). В этом случае треугольник называют треугольником, описанным около окружности .
Следствие . В любой треугольник можно вписать окружность, причем только одну. Центром вписанной в треугольник окружности является точка, в которой пересекаются все биссектрисы треугольника.
Видео:Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать

Формулы для радиуса окружности, вписанной в треугольник
Формулы, позволяющие найти радиус вписанной в треугольник окружности , удобно представить в виде следующей таблицы.
| Фигура | Рисунок | Формула | Обозначения | |||||||||||||||||||
| Произвольный треугольник |  | |||||||||||||||||||||
| Равнобедренный треугольник |  | |||||||||||||||||||||
| Равносторонний треугольник |  | |||||||||||||||||||||
| Прямоугольный треугольник |  | |||||||||||||||||||||
| Произвольный треугольник | ||
 | ||
| Равнобедренный треугольник | ||
 | ||
| Равносторонний треугольник | ||
 | ||
| Прямоугольный треугольник | ||
 | ||
| Произвольный треугольник |
 |
где
a, b, c – стороны треугольника,
S –площадь,
r – радиус вписанной окружности,
p – полупериметр

где
a, b, c – стороны треугольника,
r – радиус вписанной окружности,
p – полупериметр


где
a – сторона равностороннего треугольника,
r – радиус вписанной окружности

Видео:Радиус описанной окружностиСкачать

Вывод формул для радиуса окружности, вписанной в треугольник
Теорема 5 . Для произвольного треугольника справедливо равенство
где a, b, c – стороны треугольника, r – радиус вписанной окружности, 
с помощью формулы Герона получаем:
что и требовалось.
Теорема 6 . Для равнобедренного треугольника справедливо равенство
где a – боковая сторона равнобедренного треугольника, b – основание, r – радиус вписанной окружности (рис. 7).
то, в случае равнобедренного треугольника, когда
что и требовалось.
Теорема 7 . Для равностороннего треугольника справедливо равенство
где a – сторона равностороннего треугольника, r – радиус вписанной окружности (рис. 8).
то, в случае равностороннего треугольника, когда
что и требовалось.
Замечание . Рекомендуем читателю вывести в качестве упражнения формулу для радиуса окружности, вписанной в равносторонний треугольник, непосредственно, т.е. без использования общих формул для радиусов окружностей, вписанных в произвольный треугольник или в равнобедренный треугольник.
Теорема 8 . Для прямоугольного треугольника справедливо равенство
Доказательство . Рассмотрим рисунок 9.
Поскольку четырёхугольник CDOF является прямоугольником прямоугольником , у которого соседние стороны DO и OF равны, то этот прямоугольник – квадрат квадрат . Следовательно,
В силу теоремы 3 справедливы равенства
Следовательно, принимая также во внимание теорему Пифагора, получаем
что и требовалось.
Замечание . Рекомендуем читателю вывести в качестве упражнения формулу для радиуса окружности, вписанной в прямоугольный треугольник, с помощью общей формулы для радиуса окружности, вписанной в произвольный треугольник.
Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Центр вписанной в треугольник окружности
Где лежит центр вписанной в треугольник окружности? Что можно сказать о центре окружности, вписанной в многоугольник?
Центр вписанной в треугольник окружности является точкой пересечения биссектрис этого треугольника.
O — точка пересечения биссектрис треугольника ABC.
окр. (O; r) — вписанная.
O — точка пересечения биссектрис ∆ ABC.
Обозначим точки касания вписанной в треугольник окружности со сторонами AC, BC и AB соответственно M, K. F.

(как радиусы, проведенные в точки касания). Следовательно, треугольники AOF и AOM — прямоугольные.
У них общая гипотенуза AO, катеты OF=OM (как радиусы).
Следовательно, треугольники AOF и AOM равны (по катету и гипотенузе).
Из равенства треугольников следует равенство соответствующих углов: ∠OAF=∠OAM.
Значит, точка O лежит на биссектрисе треугольника, проведенной из вершины A.
Аналогично из равенства треугольников BOF и BOK, COM и COK доказывается, что точка O лежит на биссектрисах треугольника ABC, проведенных из вершин B и C.
Следовательно, центр вписанной в треугольник окружности лежит в точке пересечении биссектрис этого треугольника.
Что и требовалось доказать.
Доказательство теоремы можно основать непосредственно на свойстве биссектрисы угла.
1) OM=OF=OK (как радиусы),
2) OM⊥AC, OM⊥AB, OK⊥BC (как радиусы, проведённые в точку касания).
Значит точка O равноудалена от сторон углов BAC, ABC и ACB.
Так как любая точка, лежащая внутри неразвёрнутого угла и равноудалённая от сторон этого угла, лежит на его биссектрисе, то AO, BO и CO — биссектрисы треугольника ABC, O — точка их пересечения.
Аналогично, центр вписанной в многоугольник окружности (если в него можно вписать окружность) лежит в точке пересечения биссектрис этого многоугольника.
Видео:Строим вписанную в данный треугольник окружность (Задача 2).Скачать

Где всегда находится центр вписанной окружности в треугольник
Ключевые слова: окружность, описанная окружность, центр окружности, вписанная окружность, треугольник, четырехугольник, вневписанная окружность
Окружность называется вписанной в угол, если она лежит внутри угла и касается его сторон.
Центр окружности, вписанной в угол, лежит на биссектрисе этого угла.
Окружность называется вписанной в выпуклый многоугольник, если она лежит внутри данного многоугольника и касается всех прямых, проходящих через его стороны.
Если в данный выпуклый многоугольник можно вписать окружность, то биссектрисы всех углов данного многоугольника пересекаются в одной точке, которая является центром вписанной окружности.
Сам многоугольник в таком случае называется описанным около данной окружности.
Таким образом, в выпуклый многоугольник можно вписать не более одной окружности.
Для произвольного многоугольника невозможно вписать в него и описать около него окружность.
Для треуголь ника это всегда возможно.
Окружность называется вписанной в треугольник, если она касается всех трех его сторон, а её центр находится внутри окружности
- Центр вписанной в треугольник окружности лежит на пересечении биссектрис внутренних углов треугольника.
- В любой треугольник можно вписать окружность, и только одну.
- Радиус вписанной в треугольник окружности равен отношению площади треугольника и его полупериметра: $$r = frac
$$ , где S — площадь треугольника, а $$p =frac$$ — полупериметр треугольника.
Серединным перпендикуляром называют прямую перпендикулярную отрезку и проходящую через его середину.
Окружность называется описанной около треугольника, если она проходит через три его вершины.
- Вокруг любого треугольника можно описать окружность, и только одну.
- В любом треугольнике сторона равна произведению диаметра описанной окружности и синуса противолежащего угла.
- Площадь треугольника равна отношению произведения длин всех его сторон к учетверенному радиусу окружности, описанной около этого треугольника: $$R =frac$$, где S — площадь треугольника.
- Центр вневписанной окружности лежит на пересечении биссектрис внешних углов, при вершинах касаемой стороны, и биссектрисы угла при третей вершине.
Окружность, вписанная в прямоугольный треугольник
- Радиус вписанной окружности находят по формулам: $$r = frac$$, и $$r = frac$$, где a и b катеты прямоугольного треугольника, а c гипотенуза прямоугольного треугольника.
Окружность, описанная около прямоугольного треугольника
- Центр описанной окружности совпадает с серединой гипотенузы.
- Радиус равен половине гипотенузы: $$R = frac$$.
- Радиус равен медиане, проведенной к гипотенузе: $$R = m_$$.
Четырехугольник, вписанный в окружность
- Четырехугольник можно вписать в окружность, если сумма противолежащих углов равна $$180^circ: alpha + beta + gamma +delta = 180^circ$$.
- Если четырехугольник вписан в окружность, то суммы противолежащих углов равны $$180^circ$$.
- Сумма произведений противолежащих сторон четырехугольника ABCD равна произведению диагоналей: $$ABcdot DC + AD cdot BC = BD cdot AC$$.
- Площадь: $$S = sqrt$$, где $$p = frac$$ — полупериметр четырехугольника.
Окружность, вписанная в ромб
- В любой ромб можно вписать окружность.
- Радиус r вписанной окружности: $$r = frac$$, где h — высота ромба или $$r = frac <d_cdot d_>$$, где a — сторона ромба, d1 и d2 — диагонали ромба.
🎬 Видео
найти радиус окружности, описанной вокруг треугольникаСкачать

Геометрия 9 класс. Радиус описанной и вписанной окружности треугольника. Формулы радиуса.Скачать

Окружность вписана в равносторонний треугольник, найти радиусСкачать

Сможешь найти радиус вписанной окружности?Скачать

Вписанная и описанная окружности | Лайфхак для запоминанияСкачать

Сможешь найти радиус окружности? Окружность, вписанная в прямоугольный треугольникСкачать

Математика за минуту: Объяснение формулы радиуса вписанной окружности в прямоугольный треугольник.Скачать

35 Где лежит центр вписанной в треугольник окружностиСкачать

Вписанная окружность в равностороннем треугольникеСкачать

Окружность, вписанная в треугольникСкачать

РАДИУС вписанной окружности #математика #огэ #огэматематика #данирСкачать

Треугольник и окружность #shortsСкачать

Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Где искать центр описанной окружности #геометрия #огэ #егэ #математикаСкачать

ЕГЭ профиль #3 / Радиус описанной окружности / Равносторонний треугольник / решу егэСкачать