Гармонические колебания и окружность

Физика > Простое гармоническое и равномерное круговое движения

Читайте про простое гармоническое движение в равномерном движении тела по окружности: описание, центростремительное ускорение, скорость и направление, формулы.

Простое гармоническое движение формируется проекцией равномерного кругового на одной из осей плоскости x-y.

Видео:Гармонические колебания | Физика 9 класс #25 | ИнфоурокСкачать

Задача обучения

• Охарактеризовать связь между простым гармоническим и равномерным круговым движениями.

Видео:Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

Основные пункты

• В равномерном движении по окружности описывается перемещение тела по круговой траектории со стабильной скоростью. Одномерной проекцией этого процесса выступает простое гармоническое движение.
• Вектор скорости всегда касается кругового пути и постоянен по величине. Ускорение также стабильно и указывает на центр, выступающий перпендикулярным вектору скорости во все временные промежутки.
• Если тело перемещается с угловой скоростью вокруг окружности в начале плоскости x-y, то его перемещение выступает простым гармоническим движением с амплитудой (r) и угловой скоростью (ω).

Видео:Урок 327. Гармонические колебанияСкачать

Термин

• Равномерное движение по окружности – перемещение по круговой траектории со стабильной скоростью.
• Центростремительное ускорение – заставляет тело двигаться по кривой траектории. Всегда расположено перпендикулярно скорости тела и стремится к центру кривизны.

Видео:Гармонические колебанияСкачать

Равномерное круговое движение

Оно характеризует перемещение тела по круговой траектории со стабильной скоростью. Дистанция объекта к центру круга всегда остается неизменной. Если скорость объекта постоянна, то векторная нет. Тело меняет направление, поэтому меняется и скорость. Она указывает на присутствие ускорения – центростремительное. У него есть постоянная величина и оно стремится попасть в центр круга. Формируется центростремительной силой.

Видео:Гармонические колебанияСкачать

Скорость

На нижнем рисунке отображены векторы скорости и ускорения для равномерного движения по окружности в четырех различных точках орбиты. Скорость (v) соприкасается с круговым путем, поэтому две скорости не будут указывать в одном направлении. Хотя скорость постоянна, но направление все время меняется. Подобное возникает из-за ускорения, чьи точки в радиальном направлении находятся перпендикулярно скорости. Это центростремительное ускорение.

Скорость (v) и ускорение (a) в равномерном круговом движении с угловой скоростью (ω). Скорость стабильна, но всегда соприкасается с орбитой. Величина ускорения постоянна, но всегда указывает на центр вращения

Смещение вокруг кругового пути часто отображается в терминах угла (θ). Это угол, образованный между прямой линией, исходящей из центра угла до исходной позиции тел на краю и прямой линии. Угол описывает дальность движения.

Перемещающаяся по круговой траектории точка Р со стабильной угловой скоростью (ω) испытывает на себе действие равномерного кругового движения. Также отображена скорость точки вокруг круга и проекция, приравнивающаяся к v. Заметьте, что эти скорости формируют аналогичный треугольник фигуре смещения

Для пути вокруг радиуса (r), когда угол (θ) смещен, преодоленная по краю дистанция достигает s = rθ. Это можно вывести самостоятельно: окружность равна 2*pi*r, поэтому если объект смещается по всему кругу, то пройдет через угол радиуса 2pi и преодолеет дистанцию 2pi*р. Поэтому скорость движения по орбите:

(угловая скорость вращения равна ω). Получается, v – константа, а вектор скорости v также вращается со стабильной величиной при той же угловой скорости ω.

Видео:Опыты по физике. Связь гармонического колебания с равномерным движением по окружностиСкачать

Ускорение

Ускорение при равномерном движении по окружности всегда направлено внутрь и вычисляется как:

Видео:Гармонические колебания | Физика 11 класс #8 | ИнфоурокСкачать

Ускорение меняет направление, но не скорость

Простое гармоническое движение из равномерного движение по окружности.

Есть очень легкий метод вывести простое гармоническое движение из равномерного кругового. На рисунке отображен один из них. Шарик фиксируют к равномерно вращающемуся вертикальному столу, чья тень проецируется на пол. Она и выполняет простое гармоническое движение.

Тень шара, совершающая обороты со стабильной угловой скоростью на поворотном столе, перемещается вперед и назад в простом гармоническом движении

Здесь видна главная зависимость между исследуемыми движениями. Точка Р смещается вокруг круга с неизменной угловой скоростью. Она соответствует шару на поворотном столе. Проекция Р на лишенную активности ось выполняет простое гармоническое движение и соответствует тени тела.

Чтобы удостовериться, что проекция осуществляет простое гармоническое движение, отметим, что позиция х задается как:

х = Xcosθ (θ = ωt, ω – постоянная угловая скорость, X – радиус круговой траектории). Выходит, что

В этом случае 2π радиан – время для одного вращения T. То есть ω = 2π/T. Подставим в выражение:

Видео:Физика 9 класс. §25 Гармонические колебанияСкачать

Гармонические колебания

О чем эта статья:

9 класс, 11 класс, ЕГЭ/ОГЭ

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Видео:10 класс, 19 урок, График гармонического колебанияСкачать

Механические колебания

Механические колебания — это физические процессы, которые точно или приблизительно повторяются через одинаковые интервалы времени.

Колебания делятся на два вида: свободные и вынужденные.

Видео:МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫСкачать

Свободные колебания

Это колебания, которые происходят под действием внутренних сил в колебательной системе.

Они всегда затухающие, потому что весь запас энергии, сообщенный в начале, в конце уходит на совершение работы по преодолению сил трения и сопротивления среды (в этом случае механическая энергия переходит во внутреннюю). Из-за этого свободные колебания почти не имеют практического применения.

Видео:Выполнялка 53.Гармонические колебания.Скачать

Вынужденные колебания

А вот вынужденные колебания восполняют запас энергии внешним воздействием. Если это происходит каждый период, то колебания вообще затухать не будут.

• Вынужденные колебания — это колебания, которые происходят под действием внешней периодически меняющейся силы.

Частота, с которой эта сила воздействует, равна частоте, с которой система будет колебаться.

Например, качели. Если вас кто-то будет на них качать, каждый раз давая толчок, когда вы приходите в одну и ту же точку — такое колебание будет считаться вынужденным.

Это колебание все еще будет считаться вынужденным, если вас будут раскачивать из положения равновесия. Просто в данном случае амплитуда (о которой речь пойдет чуть ниже) будет увеличиваться с каждым колебанием.

Видео:5.4 Уравнение гармонических колебанийСкачать

Автоколебания

Иногда вынужденному колебанию не нужно внешнего воздействия, чтобы случиться. Бывают такие системы, в которых это внешние воздействие возникает само из-за способности регулировать поступление энергии от постоянного источника.

У автоколебательной системы есть три важных составляющих:

• сама колебательная система
• источник энергии
• устройство обратной связи, обеспечивающей связь между источником и системой

Часы с кукушкой — пример автоколебательной системы. Гиря на ниточке (цепочке) стремится вращать зубчатое колесо (храповик). При колебаниях маятника анкер цепляет за зубец, и вращение приостанавливается.

Но в результате маятник получает толчок, компенсирующий потери энергии из-за трения. Потенциальная энергия гири, которая постепенно опускается, расходуется на поддержание незатухающих колебаний.

Видео:Тема 1. Колебательное движение. Гармонические колебания. Уравнение гармонических колебанийСкачать

Характеристики колебаний

Чтобы перейти к гармоническим колебаниям, нам нужно описать величины, которые помогут нам эти колебания охарактеризовать. Любое колебательное движение характеризуется величинами: период, частота, амплитуда, фаза колебаний.

Формула периода колебаний

T = t/N

N — количество колебаний [-]

Также есть величина, обратная периоду — частота. Она показывает, сколько колебаний совершает система в единицу времени.

Формула частоты

ν = N/t = 1/T

N — количество колебаний [-]

• Амплитуда — это максимальное отклонение от положения равновесия. Измеряется в метрах и обозначается либо буквой A, либо xmax.

Она используется в уравнении гармонических колебаний:

Видео:Гармонические колебанияСкачать

Гармонические колебания

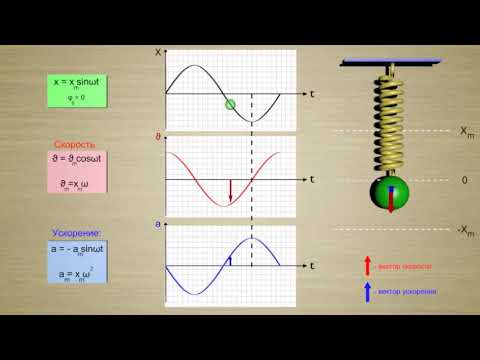
Простейший вид колебательного процесса — простые гармонические колебания, которые описывают уравнением:

Уравнение гармонических колебаний

x — координата в момент времени t [м]

xmax— амплитуда [м]

t — момент времени [с]

2πνtв этом уравнении — это фаза. Ее обозначают греческой буквой φ

Фаза колебаний

xmax— амплитуда [м]

t — момент времени [с]

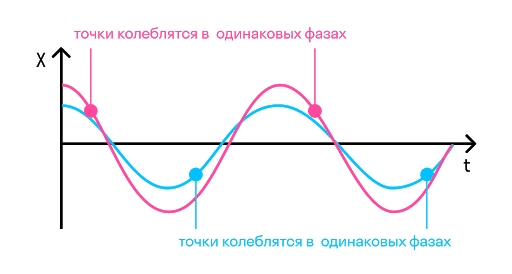
• Фаза колебаний — это физическая величина, которая показывает отклонение точки от положения равновесия. Посмотрите на рисунок, на нем изображены одинаковые фазы:

Например, в тех же самых часах с кукушкой маятник совершает колебания. Он качается слева направо и приходит в самую правую точку. В той же фазе он будет находиться, когда придет в ту же точку, идя справа налево. Если мы возьмем точку на сантиметр левее самой правой, то идя в нее не слева направо, а справа налево, мы получим уже другую фазу.

На рисунке ниже показаны положения тела через одинаковые промежутки времени при гармонических колебаниях. Такую картину можно получить при освещении колеблющегося тела короткими периодическими вспышками света (стробоскопическое освещение). Стрелки изображают векторы скорости тела в различные моменты времени.

Если изменить период, начальную фазу или амплитуду колебания, графики тоже изменятся.

На рисунке ниже во всех трех случаях для синих кривых начальная фаза равна нулю, а в последнем (с) — красная кривая имеет меньшую начальную фазу.

• В первом случае (а) красная кривая описывает колебание, у которого амплитуда больше колебания, описанного синей линии.

Во втором случае (b) красная кривая отличается от синей только значением периода — у красной период в два раза меньше.

Видео:Урок 329. Задачи на гармонические колебания - 1Скачать

Математический маятник

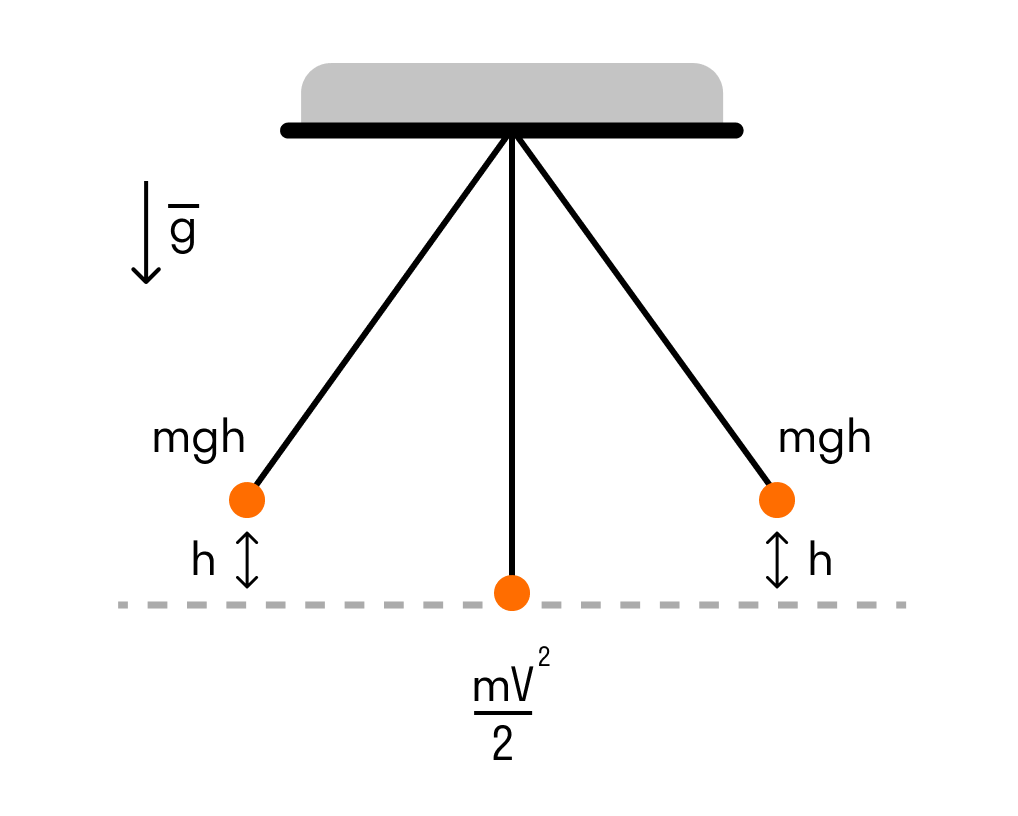
Математический маятник — отличный пример гармонических колебаний. Если мы подвесим шарик на нити, то это еще не будет математическим маятником — пока он только физический.

Математическим этот маятник станет, если размеры шарика много меньше длины нити (тогда этими размерами можно пренебречь и рассматривать шарик как материальную точку), растяжение нити очень мало, а масса нити во много раз меньше массы шарика.

Математическим маятником называется система, которая состоит из материальной точки массой m и невесомой нерастяжимой нити длиной l, на которой материальная точка подвешена, и которая находится в поле силы тяжести (или других сил).

Период малых колебаний математического маятника в поле силы тяжести Земли определяется по формуле:

Формула периода колебания математического маятника

l — длина нити [м]

g — ускорение свободного падения [м/с^2]

На планете Земля g = 9,8 м/с2

Видео:Гармонические колебанияСкачать

Пружинный маятник

Пружинный маятник — это груз, прикрепленный к пружине, массой которой можно пренебречь.

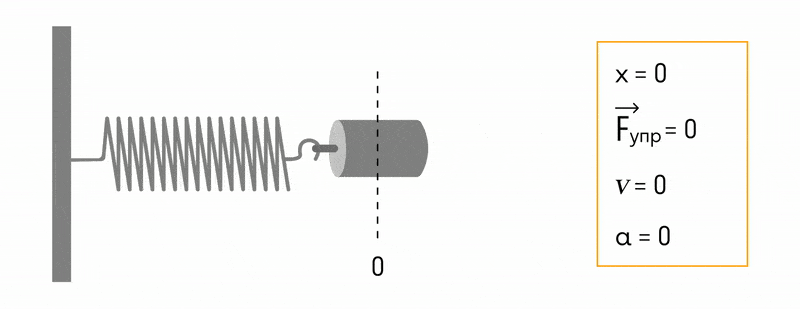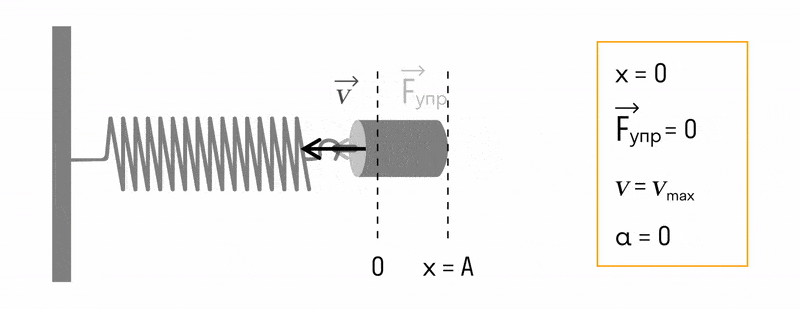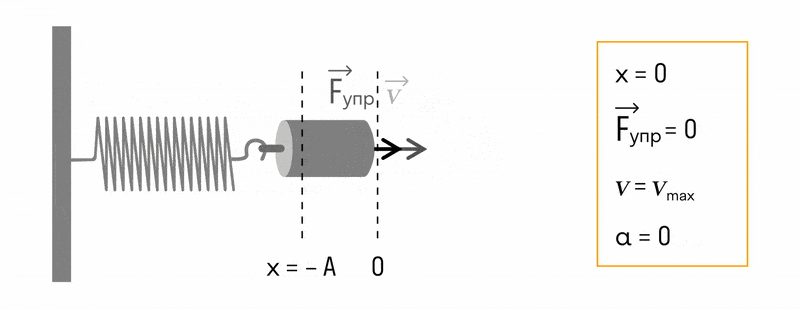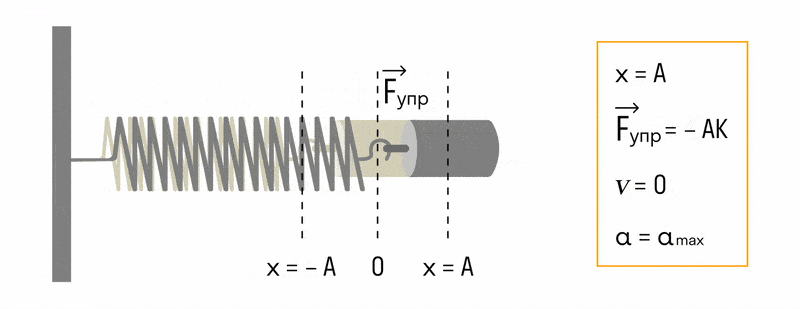
В пружинном маятнике колебания совершаются под действием силы упругости.
Пока пружина не деформирована, сила упругости на тело не действует.

Формула периода колебания пружинного маятника

m — масса маятника [кг]

k — жесткость пружины [Н/м]

Видео:Механические колебания и все что нужно про них знать. Онлайн школа EXAMhackСкачать

Закон сохранения энергии для гармонических колебаний

Физика — такая клевая наука, в которой ничего не исчезает бесследно и не появляется из ниоткуда. Эту особенность описывает закон сохранения энергии.

Рассмотрим его на примере математического маятника.

• Когда маятник отклоняют на высоту h, его потенциальная энергия максимальна.
• Когда маятник опускается, потенциальная энергия переходит в кинетическую. Причем в нижней точке, где потенциальная энергия равна нулю, кинетическая энергия максимальна и равна потенциальной энергии в верхней точке. Скорость груза в этой точке максимальна.

Онлайн-курсы физики в Skysmart не менее увлекательны, чем наши статьи!

Видео:Математика это не ИсламСкачать

Гармонические колебания

Колебательное движение – движение (изменение состояния), обладающее той или иной степенью повторяемости во времени.

Т.е. колебанием можно назвать любой вид движения, при котором через одинаковые промежутки времени повторяются кинематические характеристики движения (координата, скорость, ускорение).

Гармоническими колебаниями называются колебания, кинематические характеристики в которых меняются по закону синуса или косинуса.

Рис. 1. Колебательное движение. Вывод через окружность. Начальные условия

Для визуализации, представим вращательное движение в виде колебательного движения вдоль двух взаимно перпендикулярных осей.

Пусть тело, вращающееся по окружности радиуса A, в начале движения находилось в точке C. Пусть в начале движения радиус-вектор, описывающий выбранную точку, наклонён под углом к оси OX. Определим начальные координаты тела (исходя из проекций радиуса на оси):

Рис. 2. Колебательное движение. Вывод через окружность

Пусть через время тело, вращаясь с угловой скоростью , переместилось в точку D. При этом угол поворота радиус-вектора, относительно начального положения составил (рис. 2).

Определим текущие координаты тела тем же методом:

Учитывая, что при равномерном движении по окружности , получим:

Уравнения (5) и (6) являются законом движения материальной точки при гармонических колебаниях. Причём, одним и тем же законом, так как с тригонометрической точки зрения , тогда из (5):

• где — новый параметр, характеризующий некое другое начальное положение тела.

Таким образом, уравнения (5) и (6), по сути, являются одинаковыми уравнениями только при разных начальных условиях.

Разберём уравнение (5). Каждый из введённых параметров, имея аналог во вращательном движении, описывается по-другому в колебательном движении:

• где
  • — текущая координата тела,
  • — амплитуда колебаний (максимальное отклонение тела от положения равновесия)
  • — циклическая частота колебания
  • — время движения
  • — начальная фаза колебания
  • — текущая фаза колебания (всё, что стоит под тригонометрической функцией).

Зная общий вид колебательного движения, можем найти зависимости скорости и ускорения от времени. Для уравнения (5):

Аналогичным образом можно провести рассмотрение уравнения (6).

Проанализируем (5) и (8), исходя из внешнего вида правой части обоих уравнений, можем вывести:

Уравнение (9) называется основным уравнением гармонических колебаний.

Среди параметров колебаний также присутствуют параметры, знакомые нам по вращательному движению:

• где
  • — циклическая частота колебаний
  • — период колебаний
  • — частота колебания.

Вывод: для школьных задач почти все колебания являются гармоническими и описываются соотношениями (5), (6). Соответствующие скорость и ускорение частицы рассчитываются исходя из конкретного колебания. Параметры колебания также рассчитываются формульно.