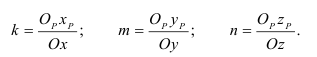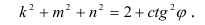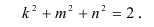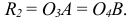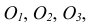Содержание:
Аксонометрическое проецирование — это способ аксонометрического проецирования состоит в том, что данная фигура вместе с осями прямоугольных координат, к которым она отнесена в пространстве, параллельно проецируется на некоторую плоскость, принятую за плоскость аксонометрических проекций (эту плоскость называют также картинной плоскостью).
- Виды аксонометрического проецирования
- Прямоугольное аксонометрическое проецирование
- Прямоугольная изометрия
- Прямоугольная диметрия
- Косоугольное аксонометрического проецирования
- Косоугольная изометрия
- Косоугольная диметрия
- Решение позиционных задач
- Пересечение прямой с плоскостью. пересечение двух плоскостей
- Пересечение тела плоскостью
- Пересечение двух тел
- Преобразование аксонометрических проекций
- Аксонометрические проекции с примерами посмотроения
- Рассмотрим способ получения аксонометрических проекций
- Изометрическая проекция отрезков и плоских фигур
- Изометрическая проекция окружности
- Изометрическая проекции геометрических тел
- Диметрическая проекция
- Диметрическая проекция окружности
- Выполнение диметрических проекций деталей
- Фронтальная изометрическая проекция
- Горизонтальная изометрическая проекция
- Косоугольная фронтальная диметрическая проекция
- Итоговое годовое тестирование по предмету «Черчение» 9 класс
- Дистанционные курсы для педагогов
- Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
- Другие материалы
- Вам будут интересны эти курсы:
- Оставьте свой комментарий
- Автор материала
- Дистанционные курсы для педагогов
- Подарочные сертификаты
- Проекционное черчение — примеры с решением заданий и выполнением чертежей
- Метод ортогонального проецирования
- Принципы построения изображений предметов на чертежах
- Виды
- Основные виды
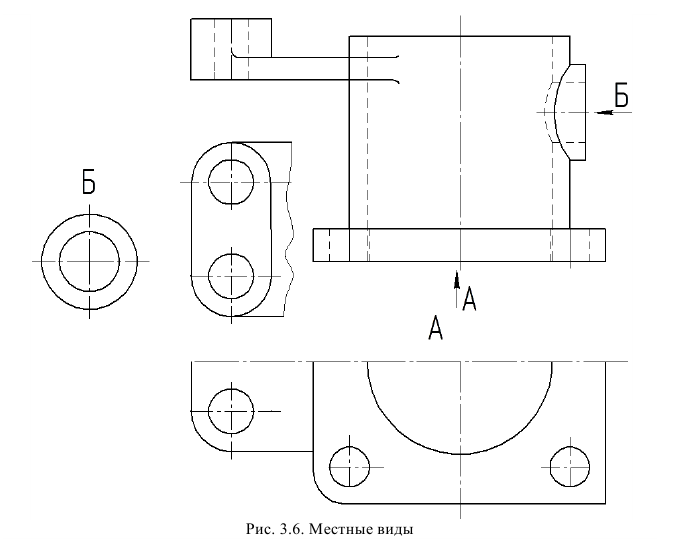
- Местные виды
- Обозначение местных видов
- Дополнительные виды
- Обозначение дополнительных видов
- Разрезы
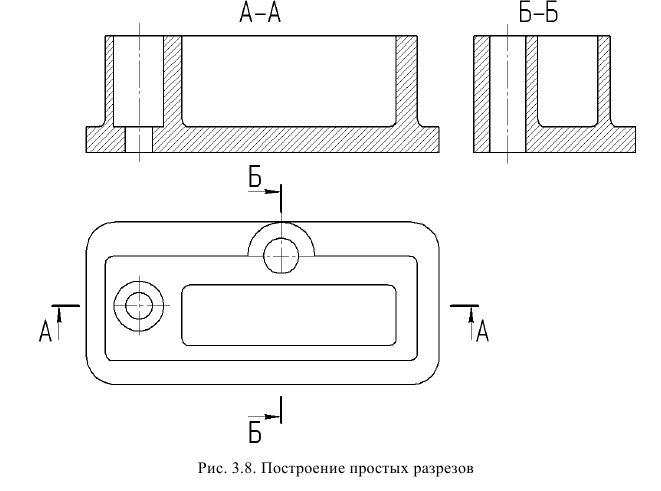
- Простые разрезы
- Местные разрезы
- Совмещение разрезов с видами
- Сложные разрезы
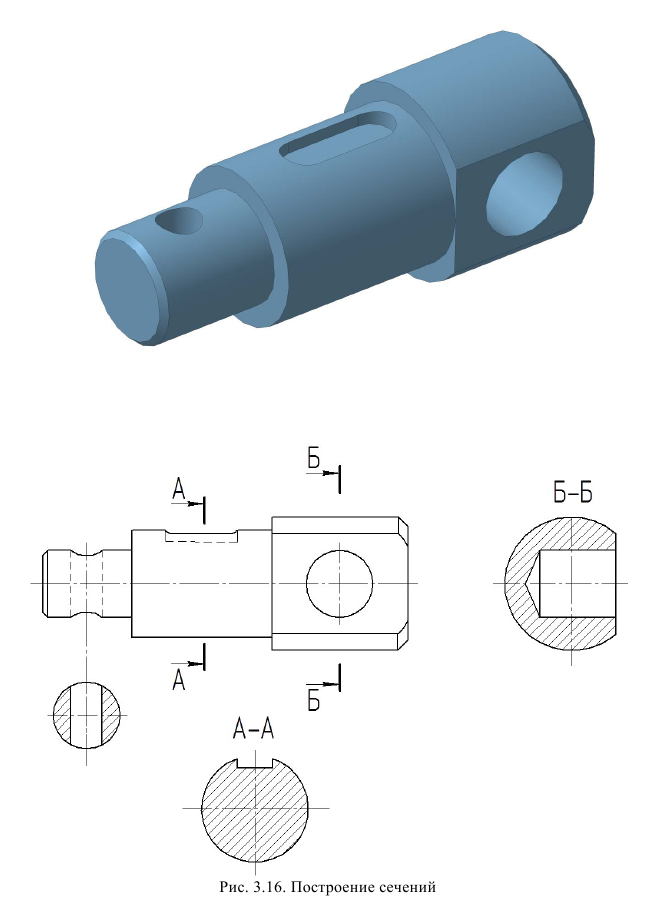
- Сечения
- Выносные элементы
- Условности и упрощения на чертежах
- Нанесение размеров
- Аксонометрические проекции предметов
- Прямоугольная изометрическая проекция
- Косоугольная фронтальная диметрическая проекция
- Разрезы в аксонометрических проекциях
- Выбор вида аксонометрии
- Построение действительной формы сечения
- Задачи проекционного черчения с решением
- Выдержки из стандартов по оформлению чертежей
- ГОСТ 2.301 — 68. Форматы
- ГОСТ 2.302 — 68. Масштабы
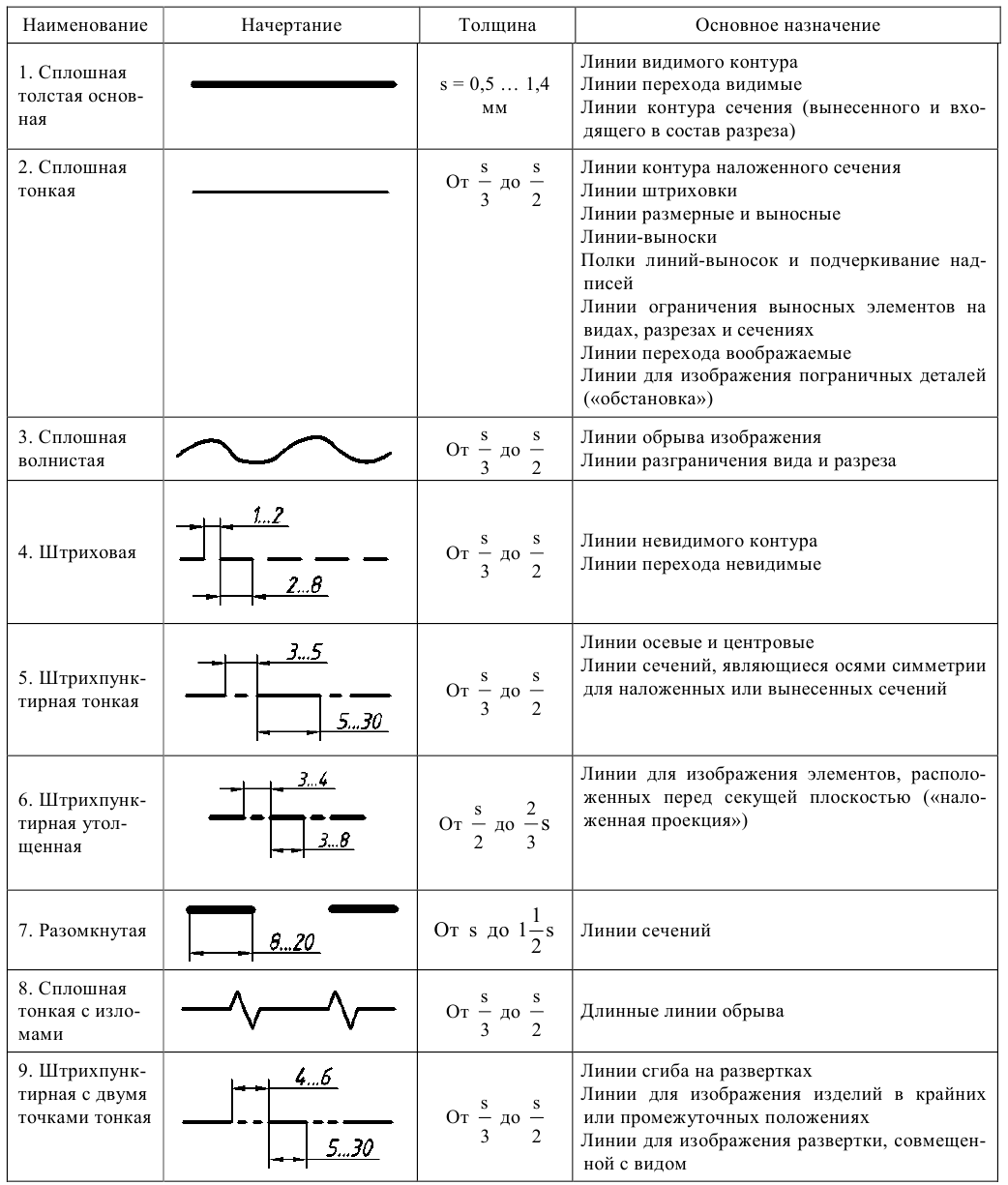
- ГОСТ 2.303 — 68. Линии
- ГОСТ 2.304 — 81. Шрифты чертежные
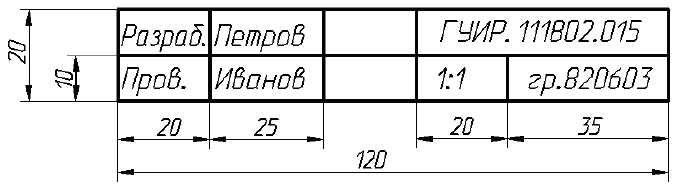
- ГОСТ 2.104 — 2006. Основные надписи
- ГОСТ 2.306 — 68. Обозначения графические материалов и правила их нанесения на чертежах
- Изображения на технических чертежах
- Прямоугольное проецирование на несколько плоскостей проекций
- Разрезы
- Сечения
- Выносные элементы
- Графическое обозначение материалов в разрезах и сечениях
- Условности и упрощения, применяемые при выполнении изображений
- Наглядные аксонометрические изображения
- Сущность метода аксонометрического проецирования
- Прямоугольная изометрия
- Прямоугольная диметрия
- Косоугольные изометрии
- Косоугольная фронтальная диметрия
- Условности и нанесение размеров в аксонометрии
- Проекционное черчение
- Изображение предметов на чертеже
- Виды
- Разрезы
- Простые разрезы
- Сложные разрезы
- Сечения
- Выносные элементы
Видео:Д.О. Технология 8 кл. Аксонометрическая проекция плоскогранных предметов. И.М.МазаеваСкачать

Виды аксонометрического проецирования
Метод ортогонального проецирования на взаимно перпендикулярные плоскости проекций П1, П2, П3 имеет существенный недостаток, состоящий в том, что представление пространственного образа предмета возможно только при условии одновременного изучения по крайней мере двух его проекций. Способ аксонометрического проецирования устраняет обозначенный недостаток, давая возможность одновременно видеть изображение предмета с двух или трёх сторон.
Аксонометрическое проецирование (от греческого άξονας – ось и µετρο – мера) – способ изображения геометрических предметов при условии параллельного проецирования на плоскость 
При аксонометрическом проецировании предмет проецируется на картинную плоскость 



Единичные отрезки ОХ, ОY, OZ проецируются на 





где φ – угол аксонометрического проецирования.
Углы 


Виды аксонометрического проецирования обусловлены числовым значением угла φ проецирования и соотношениями коэффициентов искажения 

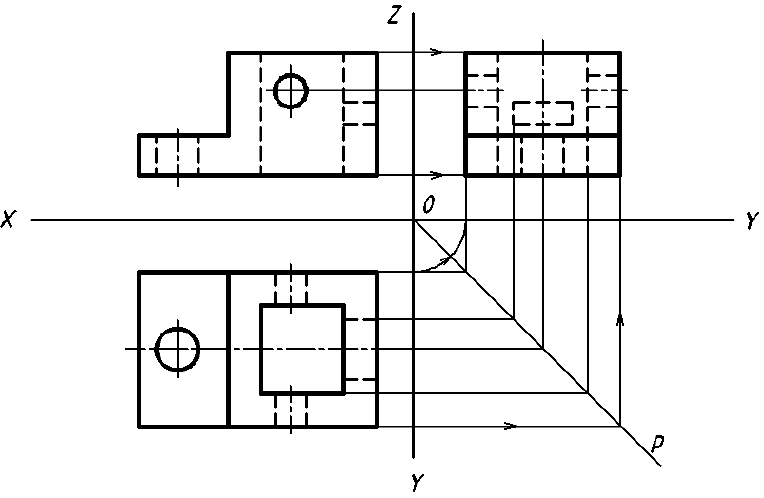
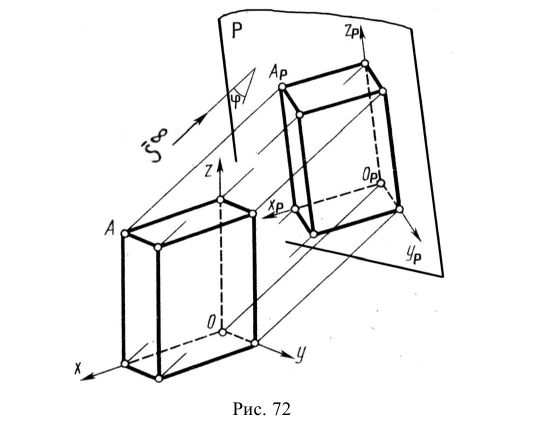
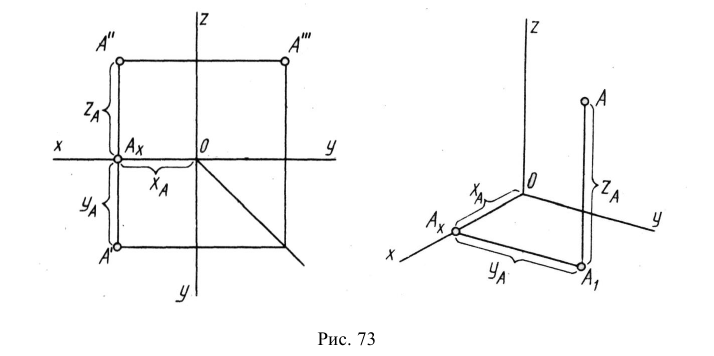
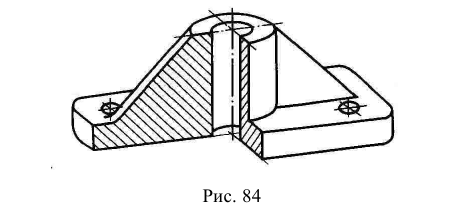
На рис. 6.1 б показан способ построения аксонометрической проекции точки А с координатами х, у, z. Для её построения из начала отсчёта 






Со всего множества аксонометрических проекций на практике применяются преимущественно такие:
а) прямоугольная изометрия (см. п. 6.2.1);
б) прямоугольная диметрия (см. п. 6.2.2);
в) косоугольная горизонтальная изометрия (см. п. 6.3.1);
г) косоугольная фронтальная изометрия (см. п. 6.3.1);
д) косоугольная фронтальная диметрия (см. п. 6.3.2).
Эти виды аксонометрического проецирования широко используются в машиностроении, строительстве и архитектуре.
Видео:58.2.1. Построить недостающие проекции точек, принадлежащих поверхности сферы, определить их видимСкачать
Прямоугольное аксонометрическое проецирование
Способ аксонометрического проецирования состоит в том, что данный предмет вместе с осями прямоугольных координат, к которым эта система относится в пространстве, параллельно проецируется на некоторую плоскость α .
Прямоугольная изометрия
Для прямоугольных аксонометрических проекций (φ = 90°) из формулы (6.1) получаем основное соотношение
Углы 

Прямоугольная изометрия (от греческого ισοµετρία – соизмеримость) – вид прямоугольного аксонометрического проецирования, в котором коэффициенты искажения k по осям одинаковы.
Из формулы (6.2) для случая 




На практике с целью упрощения коэффициенты k условно считают равными единице (k = 1). Это приводит к тому, что все действительные размеры геометрических объектов увеличиваются на 23 % (1/0,816 = 1,23).
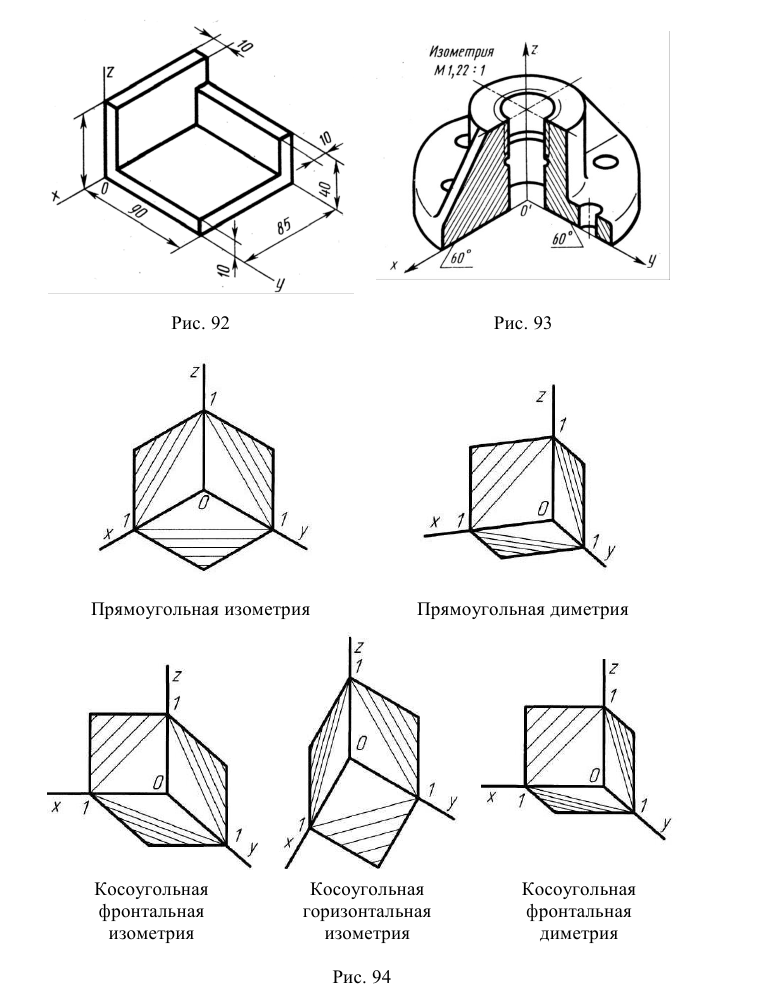
На рис. 6.4 б построена прямоугольная изометрия призмы, комплексный чертёж которой показан на рис. 6.4 а.

Для построения аксонометрической проекции геометрического объекта удобно ввести локальную систему координат (от англ. local – местный) – систему координат, связанную с заданным телом. Например, на рис. 6.4 а выбрана локальная ортогональная система координат x, y, z с центром О, совпадающим с геометрическим центром основы (пятиугольника) призмы.
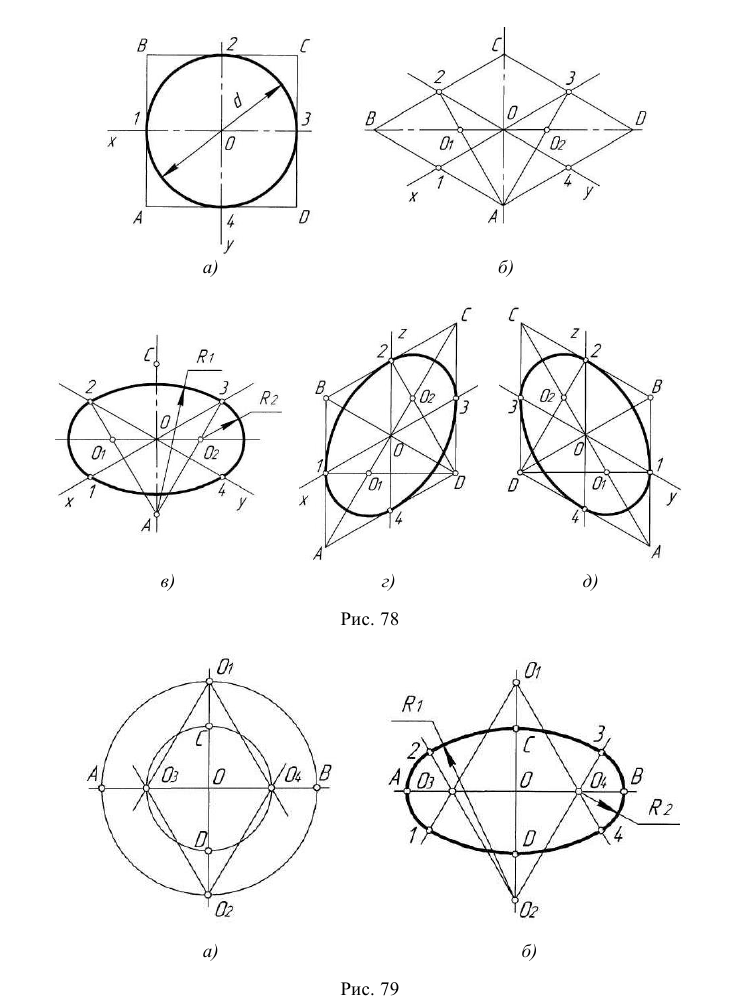
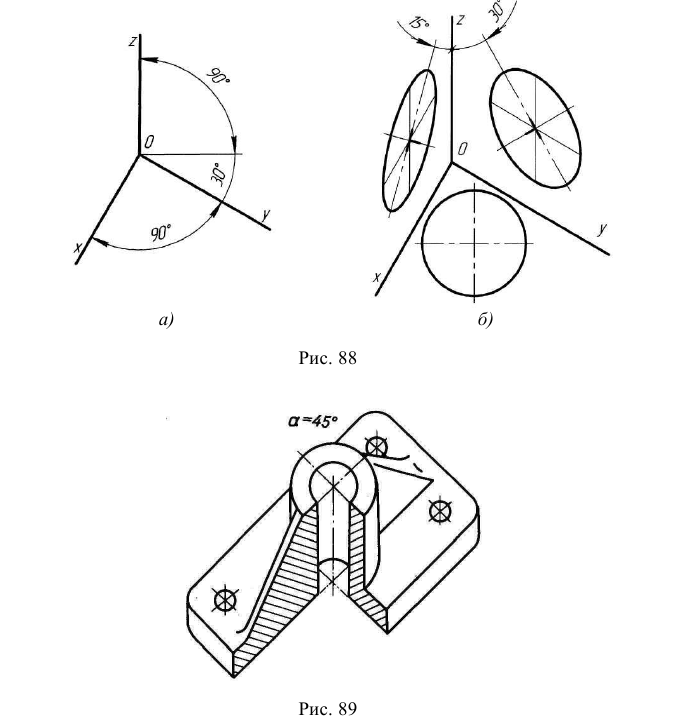
На рис. 6.5 а – е построены точные и приближённые прямоугольные изометрические проекции окружностей горизонтального, фронтального и профильного уровней. Например, прямоугольной изометрией окружности горизонтального уровня диаметром d является эллипс с горизонтальной осью 

Длины всех сторон ромба равны диаметру d заданной окружности. На практике искомый эллипс заменяется овалом (рис. 6.5 г), построенным так. Строится окружность диаметром d с центром в начале отсчёта 
















На рис. 6.5 б – в, д – е приведены точные и приближённые прямоугольные изометрические проекции окружности фронтального и профильного уровней. Отличие этих проекций от проекций окружности горизонтального уровня состоит в том, что большая ось эллипса (или овала) размещена под углом 60° к горизонту.

Прямоугольная диметрия
Прямоугольная диметрия (от греческого δυο – два, µετρο – мера) – вид прямоугольного аксонометрического проецирования, в котором коэффициенты искажения 


Из формулы (6.2) для случая 











На практике с целью упрощения коэффициенты k условно считают равными единице по осям х, z и 0,5 по оси у. Это приводит к тому, что все действительные размеры геометрических объектов увеличиваются на 6 % (1/0,943 = 1,06; 0,5/0,471 = 1,06).
На рис. 6.8 б построена прямоугольная диметрия пирамиды, комплексный чертёж которой показан на рис. 6.8 а.

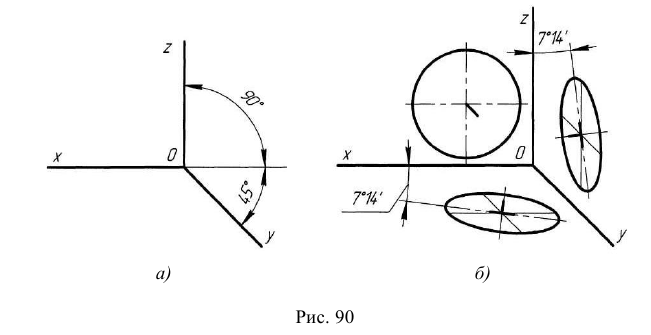
На рис. 6.9 а – е построены приближённые прямоугольные изометрические проекции окружностей горизонтального, фронтального и профильного уровней. Например, прямоугольной изометрией окружности горизонтального уровня диаметром d является эллипс со взаимно перпендикулярными осями 











Из точек 









Видео:Аксонометрические Проекции Окружности #черчение #окружность #проекции #изометрияСкачать

Косоугольное аксонометрического проецирования
Косоугольные аксонометрические проекции характеризуются двумя основными признаками: плоскость аксонометрических проекций располагается параллельно одной из граней предмета, которая изображается без искажения; направление проецирования выбирается косоугольное (составляет с плоскостью проекций острый угол), что дает возможность спроецировать и две другие грани или стороны предмета, но уже с искажением.
Косоугольная изометрия
Косоугольная изометрия – вид косоугольного аксонометрического проецирования, в котором коэффициенты искажения k по осям одинаковы. На практике используют коэффициенты k = 1.
Используются такие виды косоугольной изометрии:
а) горизонтальная изометрия, для которой углы 

б) фронтальная изометрия, для которой углы 

На рис. 6.10 а – б показана косоугольная горизонтальная изометрия точки и призмы, на рис. 6.11 а – в – окружностей горизонтального, фронтального и профильного уровней.

Косоугольная горизонтальная изометрия окружности диаметром d горизонтального уровня является окружностью такого же диаметра (рис. 6.11 а). Косоугольные горизонтальные изометрии окружности диаметром d фронтального и профильного уровней являются эллипсами, вписанными в ромбы со сторонами d (рис. 6.11 б – в).

На рис. 6.12 а – б показана косоугольная фронтальная изометрия точки и призмы, на рис. 6.13 а – в – окружностей горизонтального, фронтального и профильного уровней. Косоугольная фронтальная изометрия окружности диаметром d фронтального уровня является окружностью такого же диаметра (рис. 6.13 б). Косоугольные фронтальные изометрии окружностей диаметром d горизонтального и профильного уровней являются эллипсами, вписанными в ромбы, стороны которых равны d (рис. 6.13 а, в).


Косоугольная диметрия
Косоугольная диметрия – вид косоугольного аксонометрического проецирования, в котором коэффициенты искажения k по осям х, z одинаковы, а по оси у – вдвое меньший (0,5k). На практике применяют фронтальную диметрию, для которой k = 1, а углы 


Косоугольная фронтальная диметрия окружности диаметром d фронтального уровня является окружностью такого же диаметра (рис. 6.15 б). Косоугольные фронтальные диметрии окружности диаметром d горизонтального и профильного уровней являются эллипсами, вписанными в параллелограммы со сторонами d, d/2 (рис. 6.15 а, в).

Допускается построение фронтальной диметрии с углом 


Видео:КАК НАРИСОВАТЬ КРУГ В ИЗОМЕТРИИ (ОВАЛ В ИЗОМЕТРИЧЕСКОЙ ПРОЕКЦИИ).Скачать

Решение позиционных задач
Позиционные задачи – это задачи, решение, которых должно давать ответ на вопрос о взаимном расположении геометрических объектов как по отношению друг к другу, так и относительно системы координатных плоскостей проекций.
Пересечение прямой с плоскостью. пересечение двух плоскостей
Способ аксонометрического проецирования можно применить для решения задач начертательной геометрии.
Преимущества способа аксонометрического проецирования:
а) решение позиционных задач сопровождается наглядными изображениями предметов;
б) задачи решаются с помощью только одной аксонометрической проекции.
Недостатки способа аксонометрического проецирования:
а) сложность построения аксонометрических проекций геометрических объектов;
б) сложность или невозможность решения метрических задач;
в) необходимость в некоторых случаях дополнения аксонометрического изображения другой проекцией.
Для решения задач способом аксонометрического проецирования используется, как правило, прямоугольная изометрия.
На рис. 6.18*( * в дальнейшем верхний индекс 



На рис. 6.19 способом аксонометрического проецирования определяется линия пересечения плоскостей Σ, Ω, заданных следами. Определены точки 1, 2 пересечения двух пар одноимённых следов. Искомая линия k пересечения проходит через точки 1, 2.


Пересечение тела плоскостью
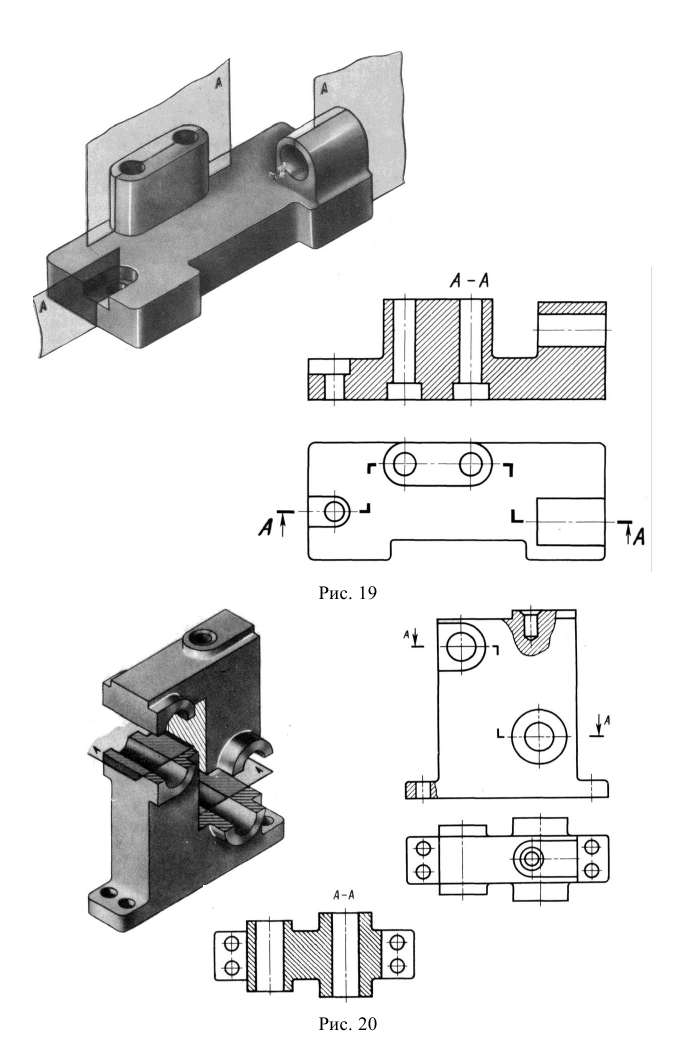
На рис. 6.20 построена линия пересечения треугольной призмы плоскостью общего положения, заданной следами. Определяются точки 1 – 5 пересечения следов плоскости с рёбрами (точка 1) и гранями (точки 2 –5) призмы. Точки 4, 5 определены с помощью вспомогательных вертикальных линий, принадлежащих граням призмы.


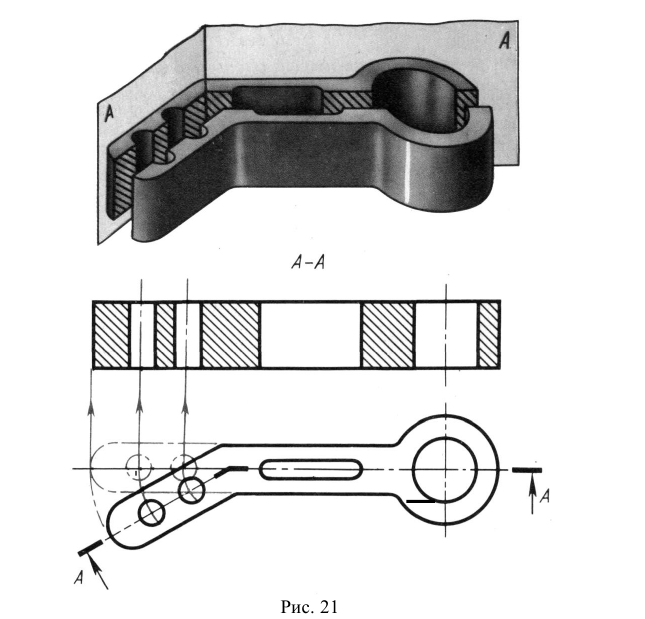
На рис. 6.21 построена линия пересечения цилиндра плоскостью общего положения. Для её определения вводятся вспомогательные секущие плоскости 
Пересечение двух тел
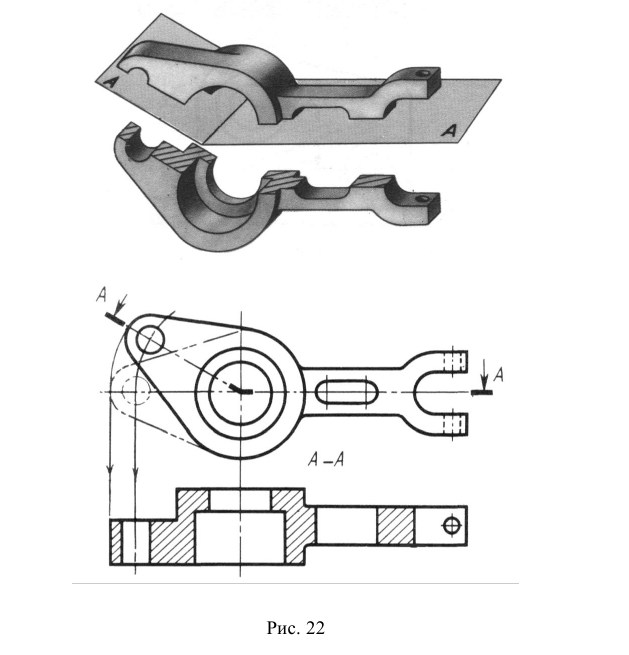
На рис. 6.22 построена линия пересечения цилиндра с призмой. Для её определения используются секущие плоскости 


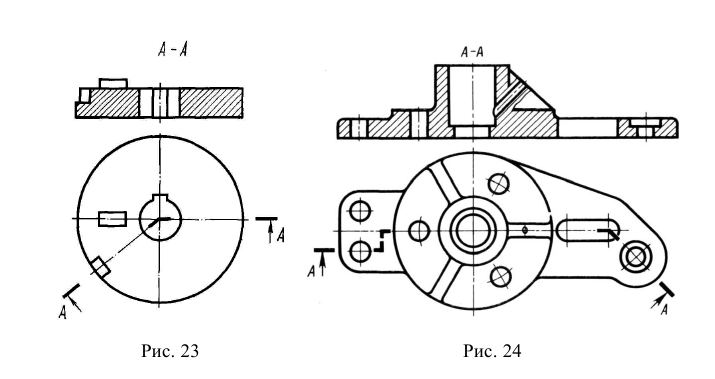
На рис. 6.23 построена линия пересечения конуса с цилиндром. Для её определения применяются фронтально-проецирующие секущие плоскости 
Преобразование аксонометрических проекций
Между аксонометрическими и ортогональными проекциями существует связь, которая позволяет переходить вот одного способа проецирования к другому и определять направление проецирования. Процедура такого перехода осуществляется с помощью построения треугольника следов картинной плоскости
На рис. 6.24 а построена система осей x 
















Для определения проекции А1 произвольной точки А по аксонометрической проекции 






Положения плоскостей проекций П2, П3 находятся аналогично, путём вращения картинной плоскости 


Видео:Задание 34 Варианты 4 (5, 6) Группа геометрических телСкачать

Аксонометрические проекции с примерами посмотроения
Аксонометрические проекции — это способ изображения геометрических предметов на чертеже при помощи параллельных проекций.
Для изображения на плоскости какого-либо предмета используют:
а) обычный рисунок;
б) способ перспективного изображения, основанный на методе центрального проецирования;
в) чертеж, состоящий из прямоугольных (ортогональных) проекций;
г) аксонометрические проекции.
Обычный рисунок изображает предмет, как он представляется глазу наблюдателя (рис. 131). Способ перспективного изображения используют при создании архитектурных проектов (рис. 132). Применение рисунка в производстве неудобно, так как он искажает форму и размеры предмета.
Чертеж дает представление о форме и размерах предмета, но часто уступает в наглядности. В этих случаях дают дополнительно изображение этого предмета в аксонометрической проекции.
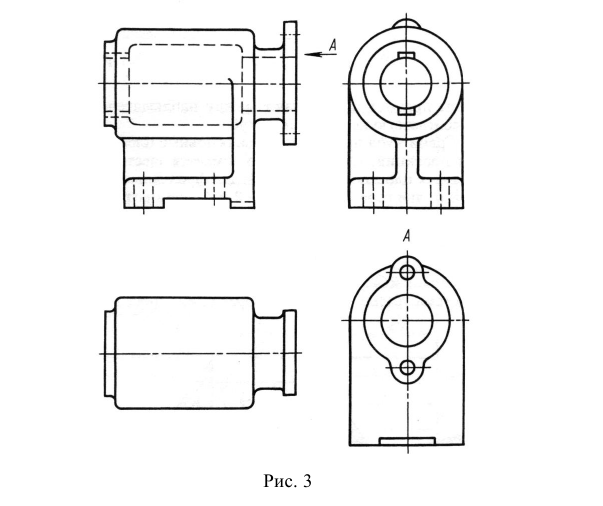
На рис. 133, а приведены ортогональные проекции предмета, по которым довольно трудно представить его форму. Значительно нагляднее аксонометрическая проекция этого предмета (рис. 133, 6).
Видео:2 2 3 построение изометрии окружностиСкачать

Рассмотрим способ получения аксонометрических проекций
На рис. 134 изображен в трех проекциях куб. Все три видимые его грани 1, 2, 3 проецируются без искажения. На рис. 135, а тот же куб поставлен относительно наблюдателя под углом и изображен в перспективе. Мы видим все три грани 1. 2, 3 одновременно, но все грани и ребра изображены с искажением. Однако можно спроецировать куб так, чтобы видеть в проекции три грани куба с меньшим искажением.
Для этого куб располагаем внутри трехгранного угла, образованного плоскостями проекций Н, V и W (рис. 135, б). Куб вместе с плоскостями проекций спроецирован на аксонометрическую плоскость проекции РV. Поэтому оси обозначаются со штрихами, т.е. х’, у’, z‘. Далее в обозначении штрихи убираем.
Таким образом, мы подошли к способу построения аксонометрических проекций. Остается определить, на какой угол целесообразнее всего повернуть предмет.
ГОСТ 2.317—69 устанавливает аксонометрические проекции, применяемые в чертежах всех отраслей промышленности и строительства (рис. 136).
В зависимости от направления проецирующих прямых и искажения линейных размеров предмета аксонометрические проекции делятся на прямоугольные и косоугольные.
Если проецирующие прямые перпендикулярны аксонометрической плоскости проекции, то такая проекция называется прямоугольной аксонометрической проекцией. К прямоугольным аксонометрическим проекциям относятся изометрическая (рис. 136. а, б) и диметрическая (рис. 136, в, г) проекции.
Если проецирующие прямые направлены не под углом 90 0 к аксонометрической плоскости проекций, то получается косоугольная аксонометрическая проекция. К косоугольным аксонометрическим проекциям относятся фронтальная изометрическая (рис. 136, д, е), горизонтальная изометрическая (рис. 136, ж, з) и фронтальная диметрическая (рис. 136, и, к) проекции.
Прямоугольные аксонометрические проекции дают наиболее наглядные изображения и поэтому чаще применяются в машиностроительном черчении.
Виды аксонометрических проекций, расположение аксонометрических осей и коэффициенты искажения линейных размеров показаны на рис. 136.
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Изометрическая проекция отрезков и плоских фигур
На рис. 136, а и б представлена изометрическая проекция.
Рассмотрим построение изометрической проекции куба.
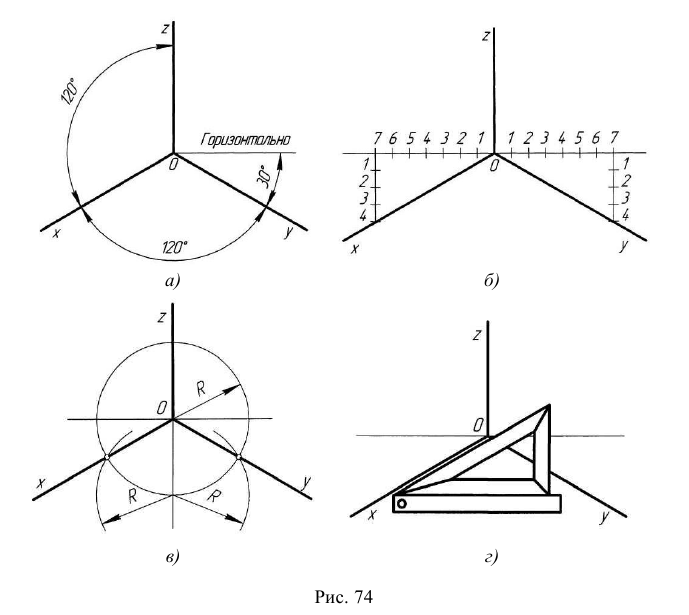
Как и при ортогональном (прямоугольном) проецировании, куб расположен внутри трехгранного угла, образованного плоскостями проекций Н, V и W. В прямоугольной изометрической проекции оси х, у, z расположатся под углом 120 0 друг к другу. Все три коэффициента искажения по аксонометрическим осям одинаковы и равны 0,82, поэтому длина ребер куба на изображении одинаковая и равна 0,82 действительной длины. Обычно для упрощения построений такого сокращения не делают; отрезки, параллельные аксонометрическим осям, откладывают действительной длины.
Простейшим элементом является точка, поэтому построение изометрических проекций начнем с точки.
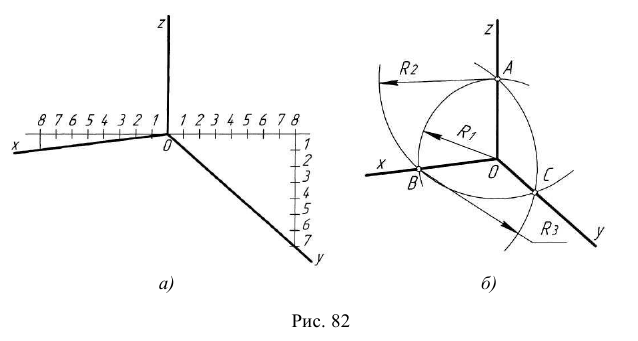
Если даны ортогональные проекции точек А и В (рис. 137, а), то известны их координаты. Для построения изометрической проекции этих точек проводят аксонометрические оси х, у и z под углом 120 0 друг к другу (рис. 137, б). Далее от начала координат О по оси х откладывают отрезок, равный координате хB точки В, в данном примере хB = 39 мм. Получим точку 1.
Из точки 1 проводят прямую, параллельную оси у, и на ней откладывают отрезок, равный координате yB, точку 2. Из точки 2 проводят прямую, параллельную оси z, на которой откладывают отрезок, равный координате zB. Полученная точка В — искомая изометрическая проекция точки В.
Аналогично строят изометрическую проекцию точки А. Так как координата z точки А равна нулю, то достаточно отложить координаты х и у (по соответствующим осям) точки А.
Аксонометрические оси изометрической проекции, а также отрезки прямых, параллельные этим осям, удобно строить с помощью угольника с углами 30 и 60 0 (рис. 137, а).
Изометрическая проекция отрезка прямой АВ может быть легко построена по двум точкам — концам этого отрезка. Найдя по координатам изометрические проекции этих точек, соединим их прямой линией. По точкам может быть выполнена изометрическая проекция любой фигуры. При этом расположение фигур относительно оси х, у и z может быть различным.
Рассмотрим, например, построение изометрической проекции правильных пятиугольников (рис. 138). В этом случае для упрощения построений рассматриваются пятиугольники, расположенные на плоскостях проекций Н, V, W. Тогда одна из координат вершин пятиугольника будет равна нулю и изометрическую проекцию каждой вершины можно строить по двум координатам, подобно построению точки А ( см. рис. 137, б).
Построив изометрические проекции вершин, соединяем их прямыми и получаем изометрическую проекцию прямоугольника.
Видео:Часть 1. Изометрическая проекция. (стр. 29)Скачать

Изометрическая проекция окружности
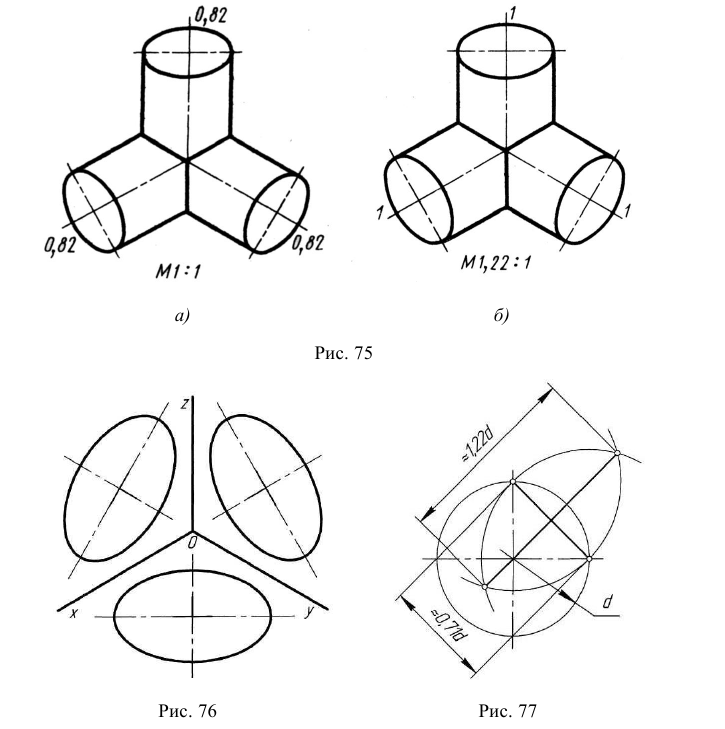
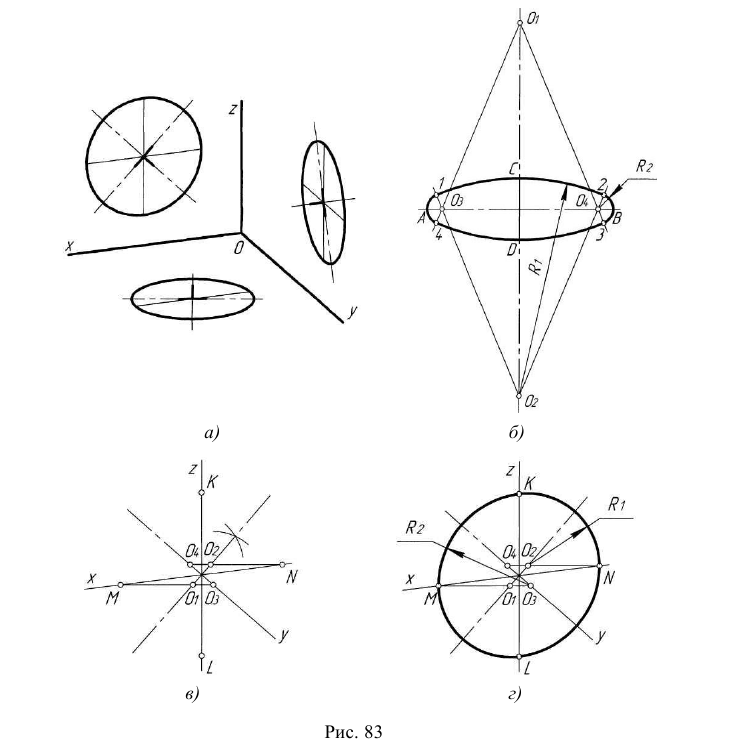
На рис. 139 изображена изометрическая проекция куба с окружностями, вписанными в его грани. Квадратные грани куба будут изображаться в виде ромбов, а окружности в виде эллипсов. Надо запомнить, что малая ось CD каждого эллипса всегда должна быть перпендикулярна большой оси АВ.
Если окружность расположена в плоскости, параллельной плоскости Н, то большая ось АВ должна быть перпендикулярна оси z, а малая ось CD— параллельна оси z (рис. 139).
Если окружность расположена в плоскости, параллельной плоскости V, то большая ось эллипса должна быть проведена под углом 90 0 к оси у.
При расположении окружности в плоскости, параллельной плоскости W, большая ось эллипса располагается под углом 90 0 к оси х.
Заметим, что большие оси всех трех эллипсов направлены по большим диагоналям ромбов.
При построении изометрической проекции окружности без сокращения по осям х, у и z длина большой оси эллипсов берется равной 1,22 диаметра d изображаемой окружности, а длина малой оси эллипса — 0,71 d (рис. 139).
В учебных чертежах вместо эллипсов рекомендуется применять овалы, очерченные дугами окружностей. Упрощенный способ построения овалов приведен на рис. 140.
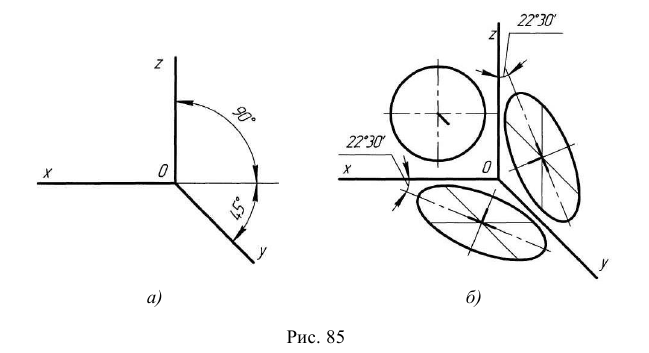
Для построения овала соответствующей изометрической проекции окружности, параллельной плоскости Н, проводят вертикальную и горизонтальную оси овала (рис. 140, а). Из точки пересечения осей О проводят вспомогательную окружность диаметром d, равным действительной величине диаметра изображаемой окружности, и находят точки n1, n2. n3, n4 пересечения этой окружности с аксонометрическими осями х и у. Из точек m1 и m2 пересечения вспомогательной окружности с осью z, как из центров радиусом R = m1* n3, проводят две дуги 23 и 14, принадлежащие овалу. Пересечения этих дуг с осью z дают точки С и D.
Из центра О радиусом ОС, равным половине малой оси овала, засекают на большой оси овала АВ точки О1 и О2. Точки 1, 2, 3 и 4 сопряжений дуг радиусов R и R1 находят, соединяя точки mt и т2 с точками O1 и О2 и продолжая прямые до пересечения с дугами 23 и 14. Из точек O1 и О2 радиусом R1=0,1 проводят две дуги.
Так же строят овалы. расположенные в плоскостях, параллельных плоскостям V и W (рис. 140, б и в).
Видео:Прямоугольные диметрические проекцииСкачать

Изометрическая проекции геометрических тел
Изображение геометрического тела в изометрической проекции, например правильной шестиугольной призмы, выполняют и такой последовательности (рис. 141).
Если основные призмы — правильный многоугольник (например, шестиугольник), то построение вершин основания по координатам можно упростить, проведя одну из осей координат через центр основания. На рис. 141 оси х, у и z проведены через центры правильных шестиугольников призмы.
Построив изометрическую проекцию основания призмы, из вершин шестиугольника основания проводим прямые, параллельные соответственно осям х, у или z (для каждой из рассматриваемых на рис. 141 призм). На этих прямых от вершин основания отложим высоту призмы и получим точки 1, 2, 3, 4, 5, 6 вершин другого основания призмы. Соединив эти точки прямыми, получим изометрическую проекцию призмы. В заключение устанавливаем видимые и невидимые линии; невидимые линии надо проводить штриховыми линиями.
На рис. 142 показано построение изометрической проекции плоской детали криволинейного очертания по комплексному чертежу. Деталь (рис. 142, а и б) расположена параллельно фронтальной плоскости проекций. На фронтальной проекции комплексного чертежа намечают ряд точек и строят их на изометрической проекции (рис. 142, в).
Через построенные точки контура кулачка проводят по лекалу кривую линию.
Параллельно оси у от найденных точек проводят прямые линии, на которых откладывают отрезки, равные А (толщине детали). Соединяя новые точки, получают контур другой плоскости детали, который также обводят по лекалу.
Аналогично строят по чертежу изометрическую проекцию кулачка.
На рис. 143 показано построение изометрической проекции (рис. 143, в) неправильной пятиугольной пирамиды по ее комплексному чертежу (рис. 143, а). Определяем координаты всех точек основания пирамиды, затем по координатам x и y строим изометрическую проекцию пяти точек — вершин основания пирамиды А, В, С. D, Е. Например, изометрическая проекция точки А получается следующим образом.
По оси х от намеченной точки О откладываем координату хА — a‘d. Из конца ее провопим прямую, параллельную оси у, на которой откладываем вторую координату этой точки уА = a‘d.
Далее строят по координатам высоту пирамиды и получают точку S — вершину пирамиды. Соединяя точку S с точками А. В. С, D н Е, получают изометрическую проекцию пирамиды.
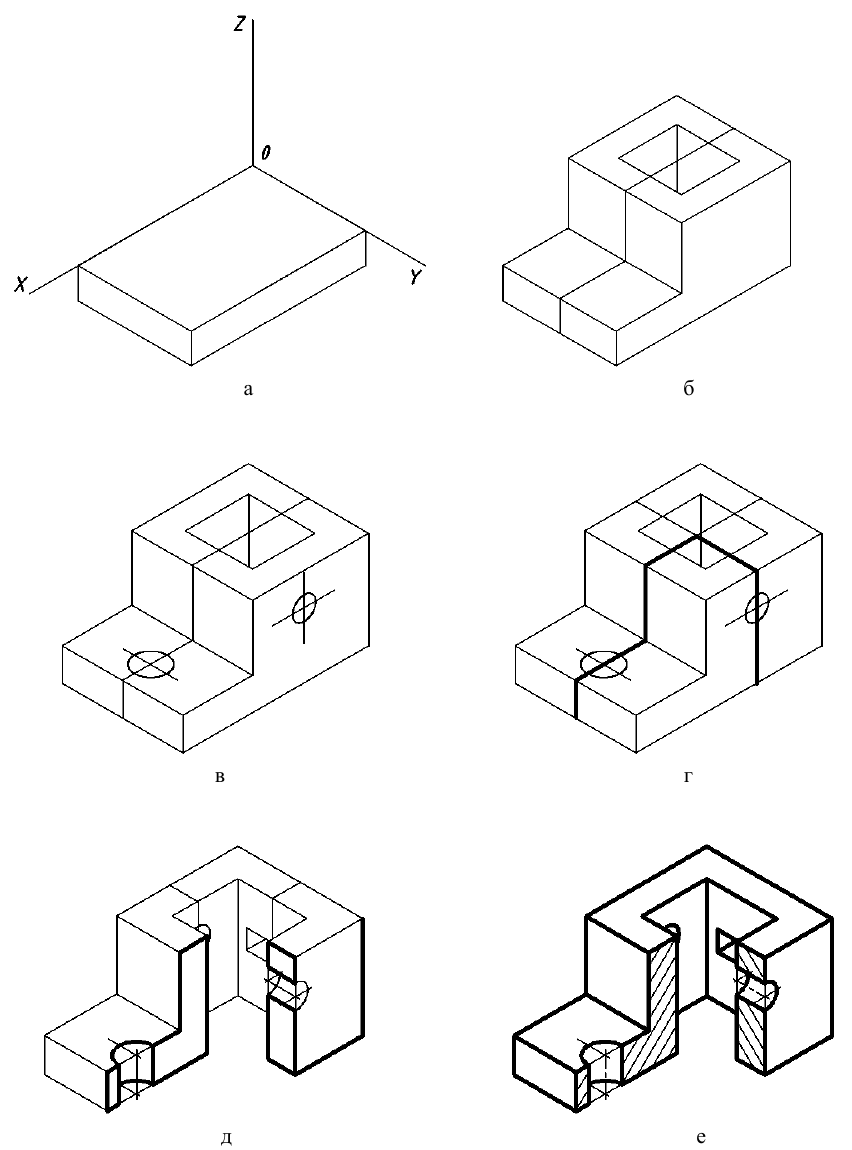
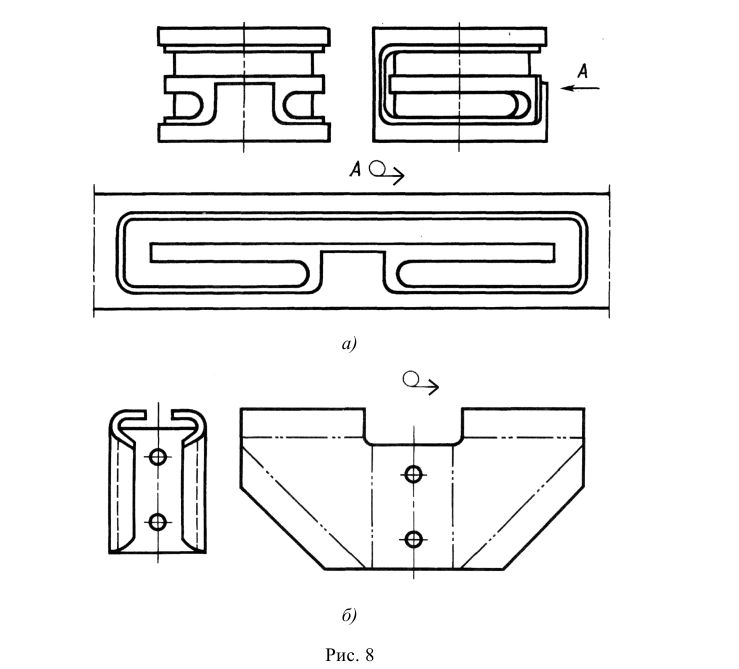
Последовательность построения изометрической проекции детали по данному комплексному чертежу (рис. 144, а) показана на рис. 144, (6 — г). Деталь мысленно разделяют на отдельные простейшие геометрические элементы, в данном случае на призматические элементы (рис. 144, б). Находят центры окружностей (рис. 144, в). Затем удаляют лишние построения, контур изображения обводят сплошной основной линией (рис. 144, г).
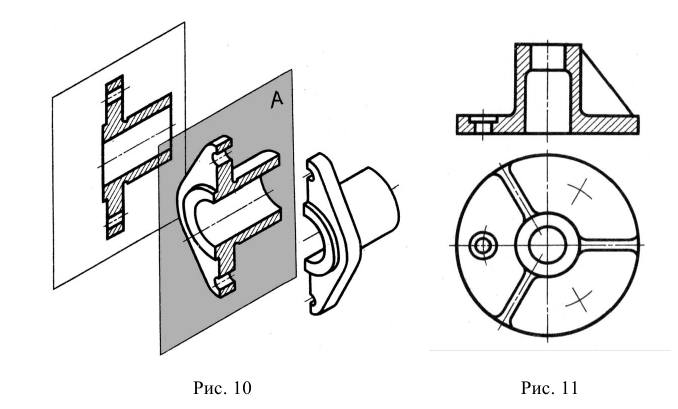
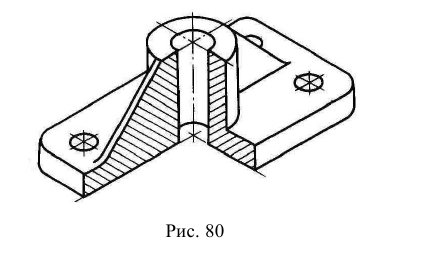
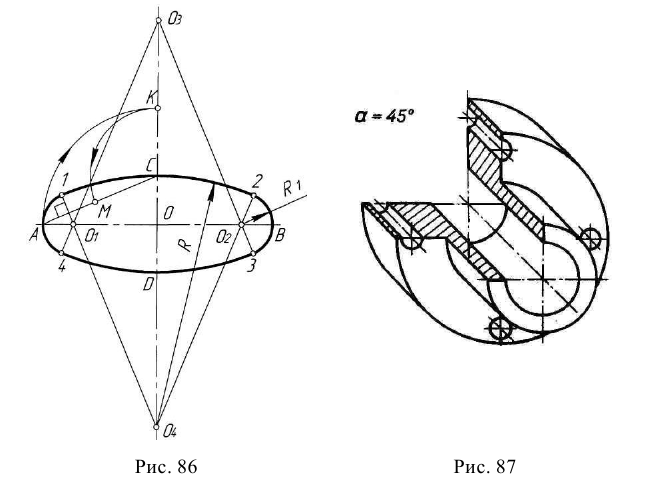
Для выявления внутренней формы предмета применяют вырез одной четверти детали. Вырез в аксонометрических проекциях можно строить двумя способами.
Первый способ. Вначале строят в тонких линиях аксонометрическую проекцию (рис. 145, а). Затем выполняют вырез, направляя две секущие плоскости по осям х и у (рис. 145, б). Удаляют часть изображаемого предмета (рис. 145, в), после чего штрихуют сечения и обводят изображение сплошными толстыми линиями (рис. 145, г).
Второй способ построения разреза при изображении деталей и аксонометрической проекции показан на рис. 146, а. Сначала строят аксонометрические проекции фигур сечения, а затем дочерчивают части изображения предмета, расположенные за секущими плоскостями (рис. 146. б).
Второй способ упрощает построение, освобождает чертеж от лишних линий.
Линии штриховки сечений в аксонометрических проекциях наносят, как показано на рис. 147, а, параллельно диагоналям проекции квадратов, которые лежат в плоскостях проекций и стороны которых параллельны аксонометрическим осям.
Штриховку сечений к изометрической проекции удобно выполнять угольником с углами 30 и 60 0 (рис. 147, б).
Изометрическая проекция шара (рис. 148) выполняется следующим образом. Из намеченного центра О проводят окружность диаметра, равною 1,22d (d — диаметр шара); это и будет изображение шара в изометрической проекции.
Если требуется построить половину, четверть или три четверти шара, то необходимо сначала вычертить овалы (рис. 148), большие оси которых АВ и CD перпендикулярны осям z и у. Тогда овалы и точки т и п пересечения этих овалов определят границы трех четвертей шара.
Видео:Как начертить овал. Эллипс вписанный в ромбСкачать

Диметрическая проекция
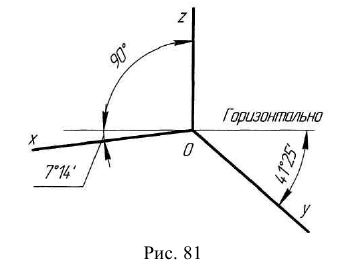
В диметрической проекции ось z — вертикальная; ось х расположена под утлом 7 0 10′, а ось у — под утлом 41 0 25′ к горизонтальной прямой (см. рис. 136, в и г).
Коэффициенты искажения по осям х и z равны 0.94. а по оси у — 0,47, но обычно отрезки прямых по осям х и у откладывают без искажения, а по оси у коэффициент искажения берут 0,5.
Все отрезки прямых линий предмета, которые были параллельны осям х, у и z на комплексном чертеже, останутся параллельными соответствующим осям в диметрической проекции.
Положение плоскости фигуры относительно осей диметрической проекции может быть различным. На рис. 149 показано, как изменяется изображение фигуры и диметрии
в зависимости от того, на какой из плоскостей проекций расположена фигура. Это изменение вызывается тем обстоятельством, что при построении вершин многоугольника их координаты по оси у в диметрической проекции сокращаются вдвое против действительной величины. Например, высота h фигуры, расположенной в плоскости H. и длина l фигуры, расположенной в плоскости W, уменьшаются в два раза.
В диметрической проекции изображения геометрических тел строят так же, как в изометрической. с учетом коэффициента искажения по оси у.
На рис. 150 показано изображение треугольной призмы в диметрической проекции. Если ребра призмы параллельны оси х или z, то размер их высоты нс меняется, но искажается форма основания. При расположении ребер параллельно оси у сокращается вдвое их высота.
Видео:Параллелепипед. Ортогональные и изометрическая проекции. Урок 1. (Часть2.ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ)Скачать

Диметрическая проекция окружности
Окружности в диметрической проекции изображаются в виде эллипсов. Большая ось АВ эллипсов во всех случаях равна 1,06 d, где d — диаметр окружности. Малые оси CD эллипсов, расположенных на плоскостях, параллельных плоскости проекций W и H, равны 0,35 d, а на плоскости, параллельной плоскости V, — O.95 d (рис. 151 ).
В диметрической проекции окружности эллипсы иногда заменяются овалами. На рис. 152 приведены примеры построения диметричеcких проекций окружностей, где эллипсы заменены овалами, построенными упрошенным способом.
Разберем упрощенное построение диметрической проекции окружности, расположенной параллельно фронтальной плоскости проекций (рис. 152, а).
Через точку О проводим оси, параллельные осям х и z. Из центра О радиусом, равным радиусу данной окружности, проводим вспомогательную окружность, которая пересекается с осями х и z в точках 1, 2, 3, 4.
Из точек 1 и 3 (по направлению стрелок) проводим горизонтальные линии до пересечения с осями АВ и CD овала и получаем точки О1 О2, О3 и О4. Приняв за центры точки О1 и О4 радиусом R = О41, проводим дуги 12 и 34. Приняв за центры точки О2 и О3, проводим радиусом R1= 022 замыкающие овал дуги 23 и 14. Большая ось АВ овала примерно будет равняться 1.06d, а малая CD— 0,95d.
Построение диметрической проекции окружности, лежащей в плоскости, параллельной профильной плоскости проекции W, приведено на рис. 152, б.
Из центра О проводим прямые, параллельные осям х и z, а также большую ось овала AB перпендикулярно малой оси CD. CD параллельна оси х. Из точки О радиусом, равным радиусу данной окружности, проводим вспомогательную окружность и получаем точки п и п1.
На прямой, параллельной оси х, вправо и влево от центра О откладываем отрезки, равные диаметру вспомогательной окружности, и получаем точки О1 и О2. Приняв эти точки за центры, проводим (по направлению стрелок) радиусом R = Otn = О2n1 дуги овалов. Пересечения полученных дуг с вспомогательной окружностью дают точки n2 и n3. Соединяя точки О2 и n1, О2 и n2 прямыми на линии большой оси АВ овала, получим точки О3 и О4. Приняв их за центры, проводим радиусом R, замыкающие овал дуги.
На рис. 152, в показано аналогичное упрошенное построение диметрнческой проекции окружности, расположенной в плоскости, параллельной горизонтальной плоскости проекций.
Видео:Построение аксонометрии моделиСкачать

Выполнение диметрических проекций деталей
Последовательность выполнения детали в диметрической проекции показана на рис. 153.
Деталь мысленно разделяют на отдельные простейшие геометрические элементы, в данном примере — на прямоугольные параллелепипеды (рис. 153, а). По оси у откладывают половину соответствующей длины ребра.
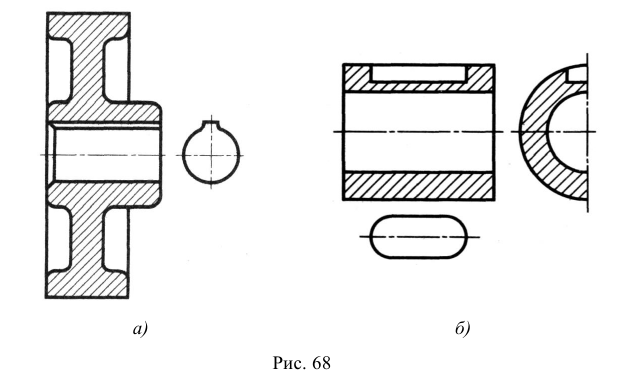
Далее находят положения центров отверстий в детали, используя метод координат, и строят овалы. Разрез детали выполняют по двум плоскостям. параллельным плоскостям V и W. На таком разрезе видно, что отверстия с вертикальными и горизонтальными осями — цилиндрические сквозные. Затем удаляют линии построения, контур изображения обводят сплошной основной линией (рис. 153, б) и штрихуют сечения (рис. 153, в).
Видео:Как начертить овал во фронтальной плоскостиСкачать

Фронтальная изометрическая проекция
Положение аксонометрических осей при изображении предметов в фронтальной изометрической проекции показано на рис. 136, д и е.
Фронтальную изометрическую проекцию выполняют без искажения по осям х, у и z. Все изображения, лежащие в плоскостях, параллельных фронтальной плоскости проекций, изображаются без искажения (рис. 136, д, е и рис. 154, а).
Окружности, расположенные в плоскостях, параллельных фронтальной плоскости проекций, проецируются на аксонометрическую плоскость проекции в окружности без искажения по осям.
Окружности, лежащие в плоскостях, параллельных плоскостям проекций Н и W, проецируются в эллипсы.
Для построения эллипсов из центров О радиусом, равным радиусу данной окружности, проводим вспомогательные окружности. Через центры О проводят прямые под утлом 22 0 30′ к аксонометрическим осям х и z и от центра откладывают большие оси эллипсов. Малые оси эллипсов должны быть перпендикулярны большим.
Длина большой оси эллипса равна 1,3d, а малой — 0.54d, где d
Предмет во фронтальной изометрической проекции следует располагать относительно осей так, чтобы окружности дуги плоских кривых находились в плоскостях, параллельных фронтальной плоскости проекций (рис. 154, б). Тогда построение их упрощается, так как они изображаются без искажений.
Видео:Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

Горизонтальная изометрическая проекция
Положения аксонометрических осей горизонтальной изометрической проекции показаны на рис. 136, ж и з.
В горизонтальной изометрической проекции линейные размеры предметов изображаются без искажения по всем трем осям. При построении осей пользуются угольниками с углами 30 и 60 0 , как показано на рис. 155, а.
Окружность, расположенная в плоскости, параллельной плоскости Н, проецируется в окружность того же диаметра (рис. 155, б, окружность 2). Окружности, лежащие в плоскостях, параллельных плоскостям проекций V и W,— в эллипсы (рис. 155, б, эллипсы 1 и 3).
Большая ось эллипса 1 равна 1.37d, а малая — 0,37d (d — диаметр изображаемой окружности). Большая ось эллипса 3 равна 1,22d, а малая — 0,71d.
На рис. 155, в изображена деталь в горизонтальной изометрической проекции.
Видео:Проекции точек на поверхности цилиндра. Урок 36.(Часть2.ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ)Скачать

Косоугольная фронтальная диметрическая проекция
Положения аксонометрических осей фронтальной диметрической проекции показаны на рис. 136, и и к. Допускается применять фронтальные диметрические проекции с углом наклона оси у 30 и 60 0 . Длина отрезков прямых, отложенных в направлении осей х и z, выполняется без искажения, а в направлении оси у линейные размеры сокращают вдвое (см. рис. 136, и и к). Эго можно видеть и на рис. 156, а—в, где даны фронтальные проекции призм и пирамиды. На рис. 156, а основание призмы (правильный шестиугольник) искажено, а на рис. 156, в — без искажения.
Окружность, лежащая в плоскости, параллельной фронтальной плоскости проекций (см. рис. 136, и и к), проецируется на аксонометрическую плоскость проекций в окружность того же диаметра, а окружности, лежащие в плоскостях, параллельных профильной и горизонтальной плоскостям проекций, — в эллипсы. Большая ось эллипсов равна l,07d, а малая ось — 0,33d (d — диаметр окружности). Для упрощения построения эллипсы заменяют овалами.
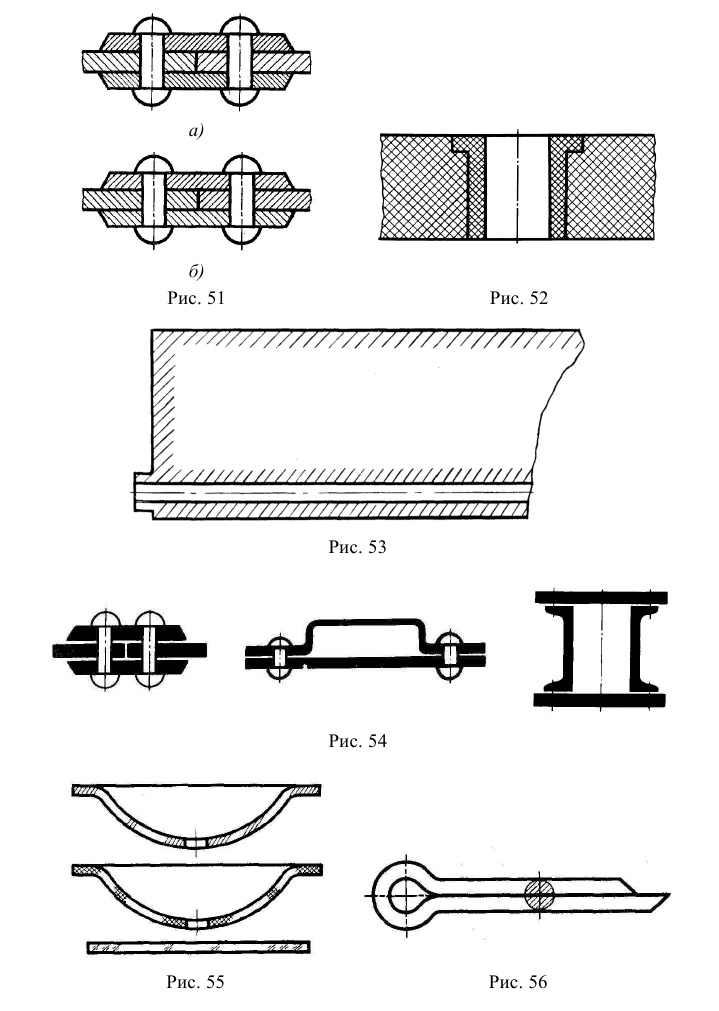
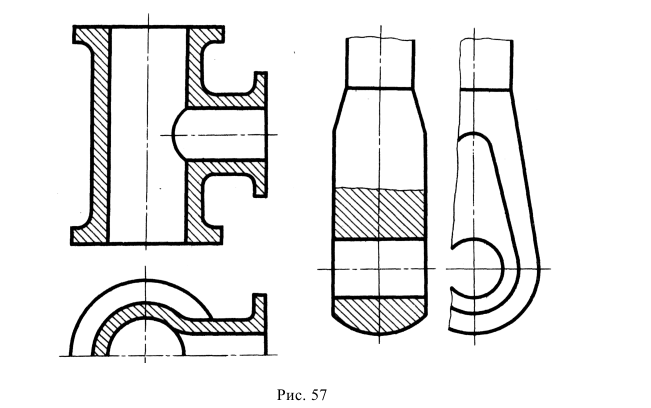
Линии штриховки сечений в аксонометрических проекциях наносят параллельно одной из диагоналей проекций квадратов, лежащих в соответствующих координатных плоскостях, стороны которых параллельны аксонометрическим осям (рис. 157, а). При нанесении размеров выносные линии проводят параллельно аксонометрическим осям, размерные линии — параллельно измеряемому отрезку (рис. 157, б).
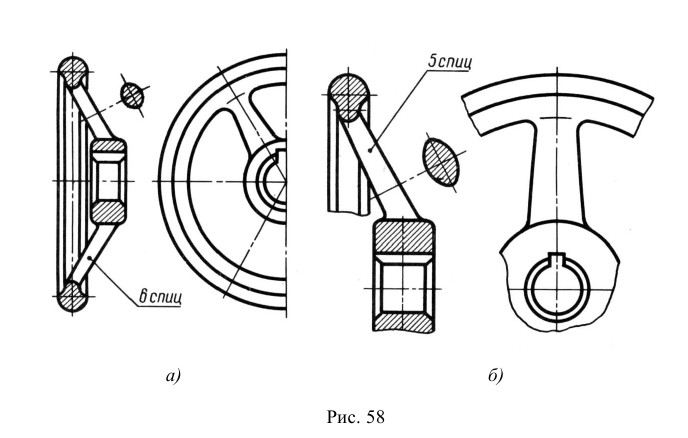
В аксонометрических проекциях спицы маховиков и шкивов, ребра жесткости и подобные элементы штрихуют (рис. 158. а).
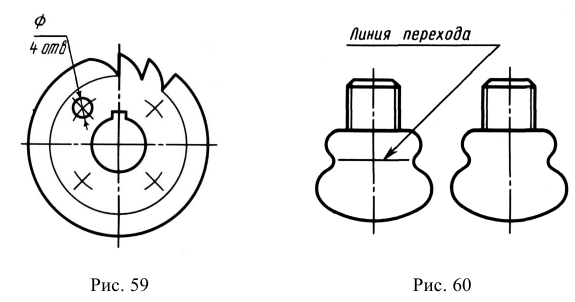
При выполнении в аксонометрических проекциях зубчатых колес, реек, червяков, резьб и подобных элементов допускается применять условности по ГОСТ 2.402-68 и ГОСТ 2.311-68 (рис. 158, б и в).
Примеры и образцы решения задач:
Услуги по выполнению чертежей:
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
Видео:Как начертить овал в горизонтальной плоскостиСкачать

Итоговое годовое тестирование по предмету «Черчение» 9 класс
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов
Сертификат и скидка на обучение каждому участнику
Итоговая работа по черчению 10 класс
за 2018-2019 учебный год
МКОУ «Толмачёвская СОШ № 61»
Итоговый контроль (выходной) – определяет качество усвоения материала, фиксирует степень и уровень подготовки по предмету, констатирует результаты обучения.
Тест составлен для контроля знаний по черчению обучающихся 8 класса по программе «Черчение», по учебнику Ботвинников А.Д., Виноградов В.Н., Вышнепольский И.С. «Черчение» ФГОС.
При выполнении заданий учитываются:
Индивидуальный подход к выполнению графического задания
Тестовая работа охватывает три основных раздела:
Правила оформления чертежей
Чтение и выполнение чертежей деталей
Задания базового уровня с 1-10 ориентированы, в основном, на проверку результативности, мягко лимитированы по времени и представлены в форме выбора правильного ответа.
Задание повышенного уровня – вопрос 11, проверяет навыки выполнения графических работ.
Критерии оценивания первой части:
Критерии оценивания второй части:
Максимальная сумма 3 балла:
1 балл – выполнен чертёж с неполным количеством необходимых линий
2 балла – правильно выполненный чертёж с небрежностью
3 балла – чертёж с необходимым количеством линий, оформленный по всем правилам оформления чертежей
Итоговый контрольный тест по ЧЕРЧЕНИЮ 10 класс 1 вариант
Какую часть формата А1 составляет формат А4.
2. Какое расположение формата А4 оговорено ГОСТом 2. 301-68.
а) вертикальное, б) горизонтальное, в) в зависимости от детали.
3. Что означает буква R перед размерным числом.
а) диаметр, б) радиус, в) толщину.
4. Что называется главным видом?
а) изображение полученное на профильной плоскости проекций.
б) изображение, полученное на фронтальной плоскости проекций
в) изображение, полученное на горизонтальной плоскости проекций
5. Фронтальная проекция предмета – треугольник, горизонтальная – квадрат с диагоналями; что это за предмет.
а) призма, б) конус, в) пирамида.
6. Даны два вида, определить, какой модели они принадлежат.
7. В результате преобразования исходной формы получилась деталь, чертеж которой представлен. Найди его.
8. Чему равно соотношение толщин линий: сплошной тонкой и сплошной толстой основной.
9. При прямоугольном проецировании проецирующие лучи направлены:
а) параллельно между собой, б) из одной точки, в) перпендикулярно друг другу.
10. Фронтальная проекция предмета – трапеция; горизонтальная – две окружности (соосные)
а) усеченный конус б) усеченная пирамида в) усеченная призма
11. Дан недочерченный чертеж. Достроить чертеж.
Итоговый контрольный тест по ЧЕРЧЕНИЮ 10 класс 2 вариант
Какую часть формата А2 составляет формат А4.
2. Какой из этих форматов имеет большие размеры.
3. Что означает буква ℓ перед размерным числом.
а) длину, б) радиус, в) толщину.
4. Что называется видом сверху?
а) изображение полученное на профильной плоскости проекций.
б) изображение, полученное на фронтальной плоскости проекций
в) изображение, полученное на горизонтальной плоскости проекций
5. Фронтальная проекция предмета – треугольник, горизонтальная – квадрат; что это за предмет.
а) призма, б) конус, в) пирамида.
6. Даны два вида, определить, какой модели они принадлежат.
7. В результате преобразования исходной формы получилась деталь, чертеж которой представлен. Найди его.
8. Чему равна толщина сплошной тонкой линии, если на чертеже толщина сплошной основной толстой линии равна 1 мм:
а) 0,5 мм, б) 0,8 мм, в) 0,3 мм.
9. Проецирующие лучи при прямоугольном проецировании направлены по отношению к плоскости
а) под острым углом, б) под прямым углом, в) параллельно плоскости.
10. Фронтальная проекция предмета – трапеция, горизонтальная – два квадрата и 4 отрезка, которые попарно соединяют соответствующие вершины.
а) усеченный конус
б) усеченная пирамида
в) усеченная призма
11. Дан недочерченный чертеж.
Ищем педагогов в команду «Инфоурок»
Видео:ПОСТРОЕНИЕ ОВАЛА │ КАК НАЧЕРТИТЬ ОВАЛ ПРИ ПОСТРОЕНИИ АКСОНОМЕТРИИ │ Урок #61Скачать

Дистанционные курсы для педагогов
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 539 386 материалов в базе
«Актуальность создания школьных служб примирения/медиации в образовательных организациях»
Свидетельство и скидка на обучение каждому участнику
Другие материалы
- 16.08.2020
- 136
- 4
- 15.08.2020
- 577
- 35
- 02.08.2020
- 515
- 42
- 01.08.2020
- 220
- 4
- 01.08.2020
- 213
- 7
- 30.07.2020
- 164
- 11
- 27.07.2020
- 327
- 21
- 27.07.2020
- 232
- 5
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 20.08.2020 1515
- DOCX 163.6 кбайт
- 36 скачиваний
- Оцените материал:
Настоящий материал опубликован пользователем Маслова Ольга Викторовна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 3 года и 5 месяцев
- Подписчики: 0
- Всего просмотров: 8572
- Всего материалов: 14
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Видео:ПРОЕКЦИИ ТОЧЕК на поверхности шара (сферы). Построение трех проекций точек на заданной сфереСкачать

Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
В России классы будут переводить на дистант, если заболели 20% детей
Время чтения: 1 минута
Минобрнауки подготовит государственный рейтинг университетов
Время чтения: 1 минута
Полный перевод школ на дистанционное обучение не планируется
Время чтения: 1 минута
В Калужской области школьники уйдут на каникулы с 7 по 20 февраля
Время чтения: 1 минута
Володин призвал выработать единые нормы организации групп продленного дня
Время чтения: 2 минуты
В Госдуме предложили доплачивать учителям за работу в классах, где выявлен ковид
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Видео:видеолекция №3, изометрия, 1 частьСкачать

Проекционное черчение — примеры с решением заданий и выполнением чертежей
Проекционное черчение – это учебная дисциплина, которая устанавливает правила выполнения и чтения чертежей.
Проекционное черчение является основным разделом курса черчения, в котором изучаются правила, условности и практические приемы построения изображений в ортогональных и аксонометрических проекциях, установленные стандартами (ЕСКД, ГОСТ). На данной странице собран курс лекций по всем темам проекционного черчения с примерами по предмету «Проекционное черчение«.
Для построения изображений (проекций) объектов или предметов на плоскости применяют метод проецирования. Чертежи которые сделаны таким методом, называются проекционными. При выполнении чертежей технических форм используются метод ортогонального проецирования.
Содержание:
Любое техническое изделие (прибор, машина, отдельная деталь и пр.) изготавливают на предприятии по чертежам. Чертеж должен содержать полную информацию, необходимую для изготовления изделия, и в первую очередь его изображение. Главным требованием, предъявляемым к изображениям, является то, что они должны точно воспроизводить форму внешних и внутренних поверхностей изделий. Для обеспечения этого требования необходимо, чтобы изображения на чертежах были построены определенным способом по определенным правилам, которые изложены в ГОСТ 2.305 -2008 [1].
Часть курса «Начертательная геометрия и инженерная графика», в которой изучают правила построения изображений, называют проекционным черчением.
В проекционном черчении в качестве объекта для построения изображений выступает предмет — обезличенная деталь, а сами изображения должны быть построены по методу ортогонального (прямоугольного) проецирования.
Чертежи должны быть оформлены по единым и обязательным для всех правилам, изложенным в стандартах ЕСКД.
Видео:Построение окружности в диметрииСкачать

Метод ортогонального проецирования
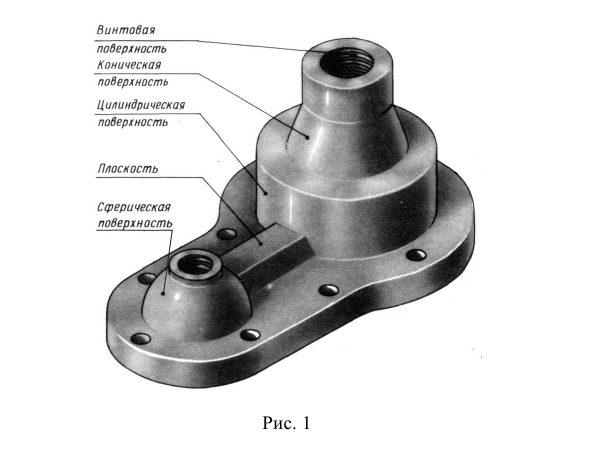
Проецирование — это процесс получения изображения предмета на плоскости, например бумаге, экране и т. д. (рис. 1). При этом:
- предмет располагается между наблюдателем и этой плоскостью (она называется плоскостью проекций);
- через опорные и другие точки предмета проводятся проецирующие лучи до пересечения их с плоскостью проекций;
- множество точек пересечения будет образовывать на плоскости проекций изображение предмета или, как его еще называют, проекцию предмета.
Таким образом, можно назвать проецированием фотографирование предмета или получение его тени в солнечный день на любом экране.
Ортогональное проецирование характеризуется тем, что проецирующие лучи параллельны между собой и перпендикулярны к плоскости проекций. Метод ортогональных проекций является основным при построении машиностроительных чертежей, так как позволяет точно передавать форму и размеры предметов на их проекциях.
Принципы построения изображений предметов на чертежах
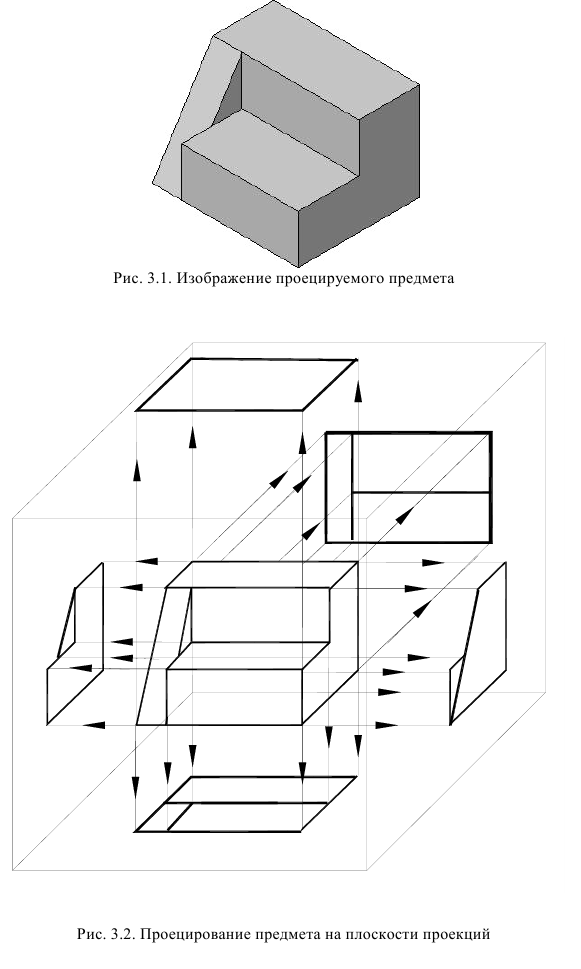
По изображению предмета, полученному на одной плоскости проекций, даже если оно построено по методу ортогонального проецирования, нельзя полностью представить формы всех его поверхностей. Так, по фронтальной проекции предмета, показанного на рис. 1, можно судить только о двух его измерениях — высоте и длине. Остаются невыявленными ширина предмета, форма отверстия и паза. Очевидным является вывод: чтобы получить полную информацию о форме всех частей предмета, необходимо построить его изображения со всех сторон. Поэтому при составлении технических чертежей предмет проецируют не на одну, а на несколько взаимно перпендикулярных плоскостей проекций.
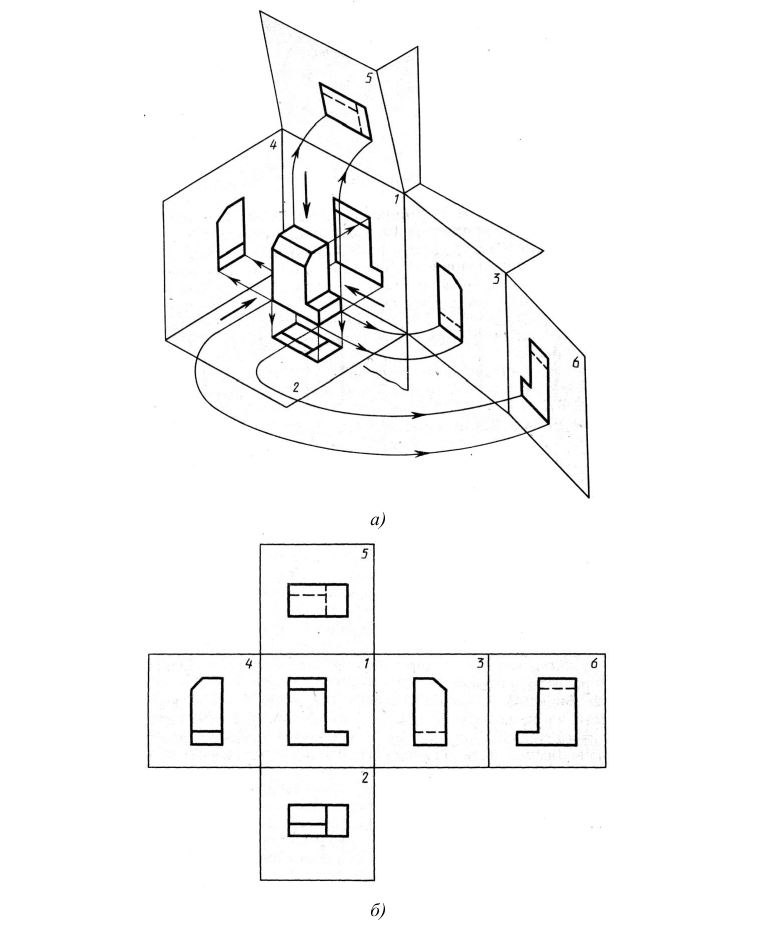
По ГОСТ 2.305 — 2008 [1] основные изображения предмета получают на гранях пустотелого куба, внутри которого помещен предмет (рис. 2). Грани выступают в качестве основных плоскостей проекций. Построение ортогональной проекции на каждой грани производится так, как показано на рис. 1, т. е. наблюдатель располагается таким образом, чтобы предмет находился между ним и соответствующей гранью куба. На рис. 3 указаны направления взгляда наблюдателя при таком проецировании. Проецирование в направление 2 на рис. 3 приведет к построению изображения па грани 2 и т. д. Разрезая куб по ребрам, развертывают все его грани до совмещения с фронтальной плоскостью проекций. Получают чертеж предмета, включающий шесть изображений (см. под разд. 3.1).
При ортогональном проецировании необходимо соблюдать следующие правила:
- предмет ориентируют внутри куба так, чтобы большинство его граней и ребер были расположены параллельно граням куба (в этом случае грани и ребра предмета проецируются без искажений их формы и размеров);
- изображение на фронтальной плоскости проекций (см. рис. 2, грань 1) принимают за главное. Предмет размещают так, чтобы изображение на этой плоскости давало наиболее полное представление о его форме. Длинные предметы принято располагать горизонтально.
Изображения в зависимости от содержания делят на виды, разрезы и сечения.
Виды
Вид — это изображение обращенной к наблюдателю видимой части поверхности предмета. Виды разделяют на основные, дополнительные и местные.
Основные виды
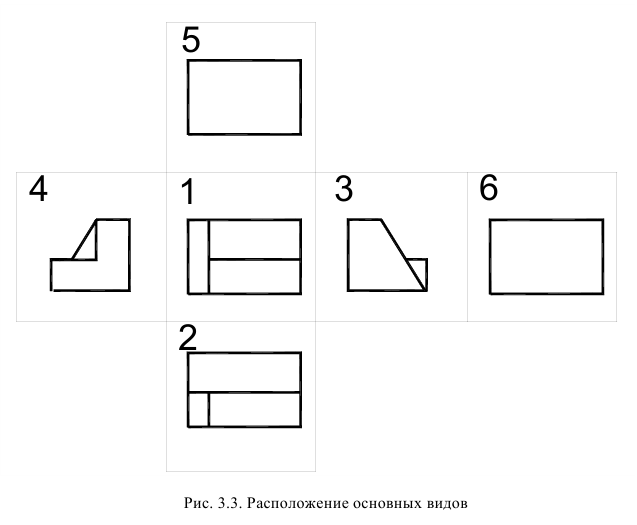
Проекции предмета, полученные на гранях куба (см. рис. 2), развернутых в одну плоскость, называются основными видами. На рис. 4 приведена схема расположения основных видов на чертеже и их наименование.
Наименование каждого вида определяется направлением взгляда наблюдателя при проецировании. За основу построения чертежа принимают вид спереди — главный вид предмета. Все шесть видов располагаются в проекционной связи относительно главного вида. Такое расположение видов утверждено ГОСТ 2.305 — 2008 [1] и является обязательным при выполнении чертежей. Нарушение проекционной связи в расположении видов допускается при действительной необходимости в этом. Видимые контуры предмета на чертеже принято изображать основной линией (сплошной толстой линией толщиной от 0,5 до 1,4 мм включительно), контуры невидимых поверхностей — штриховой линией. Оси симметрии изображений и центровые линии окружностей показывают штрихпунктирной линией. Штриховые и штрихпунктирные линии выполняют линией в 2 . 3 раза тоньше основной линии. Начертание линий дано в ГОСТ 2.303 — 68 [4].
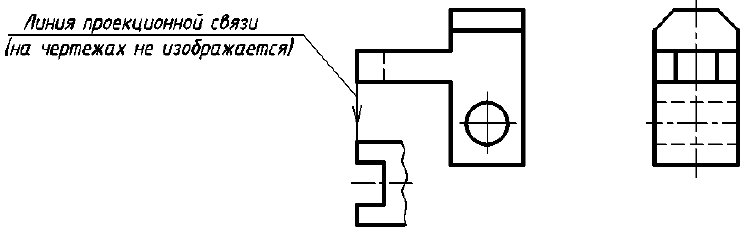
Контуры граней куба и линии проекционной связи на чертежах не изображают.
При выполнении чертежа любого технического изделия необходимо руководствоваться очень важным стандартным правилом: количество изображений па чертеже должно быть минимальным, но достаточным для полного представления о конструкции всех элементов предмета. Анализ основных видов на рис. 4 показывает, что вид справа несет такую же информацию о форме предмета, что и вид слева. То же можно сказать о видах снизу и сверху, сзади и спереди. Таким образом, для рассматриваемого предмета можно ограничиться тремя основными видами: спереди, сверху и слева (рис. 5).
Рис. 5. Оптимальное количество видов предмета, показанного на рис. 2
Рассмотрим обозначение основных видов. Если основные виды находятся в проекционной связи с главным видом (т. е. так, как показано на рис. 4 и рис. 5), то они не обозначаются.
На практике иногда приходится отдельные основные виды располагать на чертежах с нарушением их проекционной связи с главным видом. Как правило, это выполняют с целью уменьшения формата чертежа, что достигается рациональной компоновкой изображений. Рациональной считается такая компоновка, при которой изображения располагаются на поле чертежа равномерно, т. е. приблизительно с одинаковым расстоянием между ними и от изображений до внутренней рамки чертежа. Рассмотрим этот случай. Пусть предмет имеет форму, для пояснения которой на чертеже необходимо построить четыре основных вида. При стандартном расположении видов они заполнят поле чертежа нерационально (рис. 6). Если же вид справа разместить под видом слева, то изображения займут меньший формат и будут расположены на нем рационально (рис. 7).
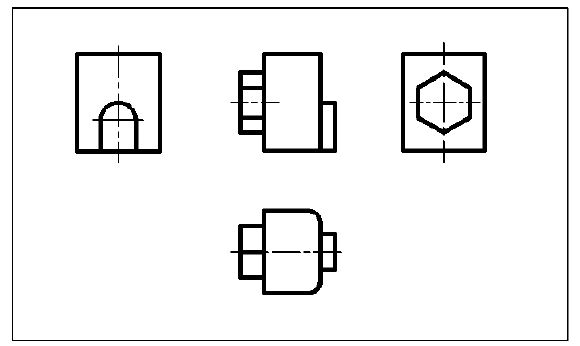
Рис. 7. Рациональная компоновка основных видов (вид справа находится не в проекционной связи с главным и должен быть обозначен)
Если какой-либо основной вид не находится в проекционной связи с главным, то он должен быть обозначен (см. вид справа на рис. 7):
- должно быть указано стрелкой около соответствующего вида (как правило главного) направление проецирования;
- над стрелкой и построенным по указанному стрелкой направлению видом должна быть нанесена одна и та же прописная буква русского алфавита.
Для обозначения основных, местных и дополнительных видов, а также разрезов и сечений, применяют прописные буквы русского алфавита, кроме букв Ё, 3, Й, О, Ч, X, Ь, Ы, Ъ, начиная с буквы А в порядке их расположения без пропусков и повторений.
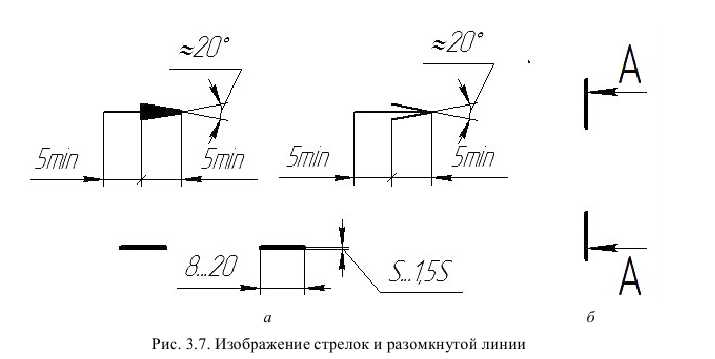
Стрелки, применяемые для указания направления взгляда, должны иметь форму и размеры, приведенные на рис. 8, а. На рис. 8, б, в даны другие варианты начертания стрелок.
Рис. 8. Размеры и допустимые варианты формы стрелок, указывающих направление взгляда
Местные виды
Если руководствоваться правилом о том, что на чертеже должно быть минимальное количество изображений (см. подразд. 3.1), то при анализе изображений, представленных на рис. 7, видно, что вид справа (вид Л) нужен исключительно для того, чтобы показать форму выступа, а остальная часть вида А -габаритный контур предмета — повторяет такой же контур на виде слева. Для того чтобы в подобных случаях исключить повторяющуюся информацию, применяют местные виды (рис. 9, а, б; вид Л).
Местным видом называется изображение отдельного ограниченного места поверхности предмета, параллельной плоскости проекций (грани куба). Местный вид может быть частью основного вида, а может быть видом на участок внутренней поверхности предмета.
Местный вид может быть ограничен линией обрыва (см. рис. 9, а), по возможности в наименьшем размере, или не ограничен (см. рис. 9, б). 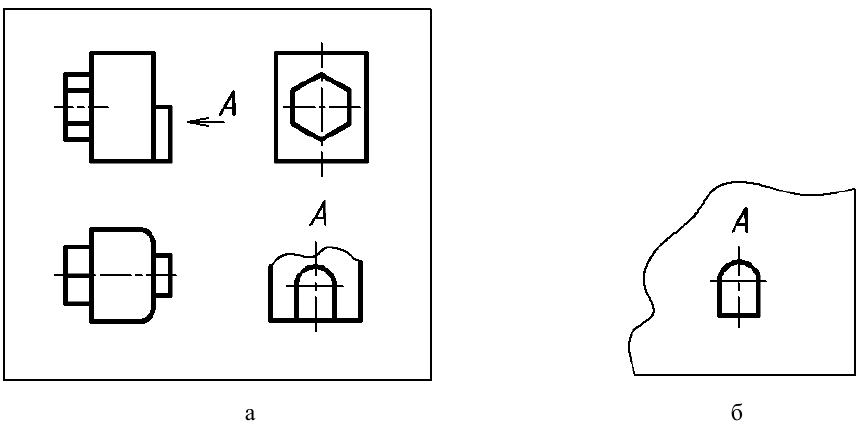
а — ограниченного линией обрыва; б — не ограниченного линией обрыва
Обозначение местных видов
Если местный вид не находится в проекционной связи с соответствующим изображением предмета, то он должен быть обозначен. Пример обозначения см. на рис. 9, а. Здесь местный вид А — это часть основного вида справа, который не находится в проекционной связи с главным.
Если местный вид находится в непосредственной проекционной связи с соответствующим изображением, то он не обозначается (рис. 10).
Дополнительные виды
В разд. 2 было указано, что при ортогональном проецировании предмет ориентируют внутри куба так, чтобы большинство его плоских поверхностей были параллельны граням куба. Только при таком расположении на гранях куба будут получены проекции, которые передадут действительную без искажений форму и размеры указанных плоских поверхностей предмета.
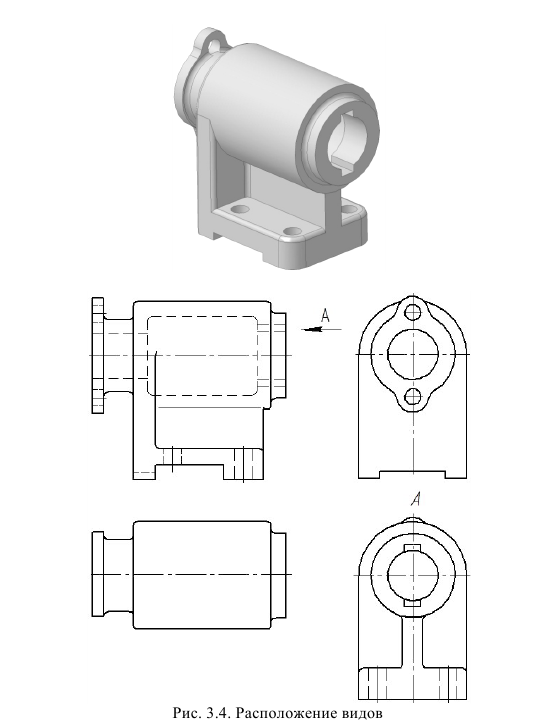
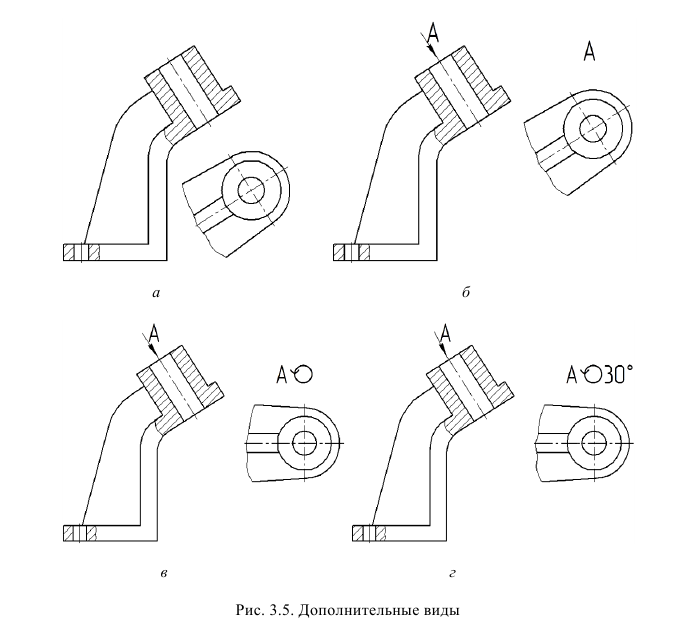
Если какую-либо часть предмета невозможно показать на основных видах без искажения формы и размеров, то применяют дополнительные виды, получаемые на плоскостях, непараллельных основным плоскостям проекций (рис. 11).
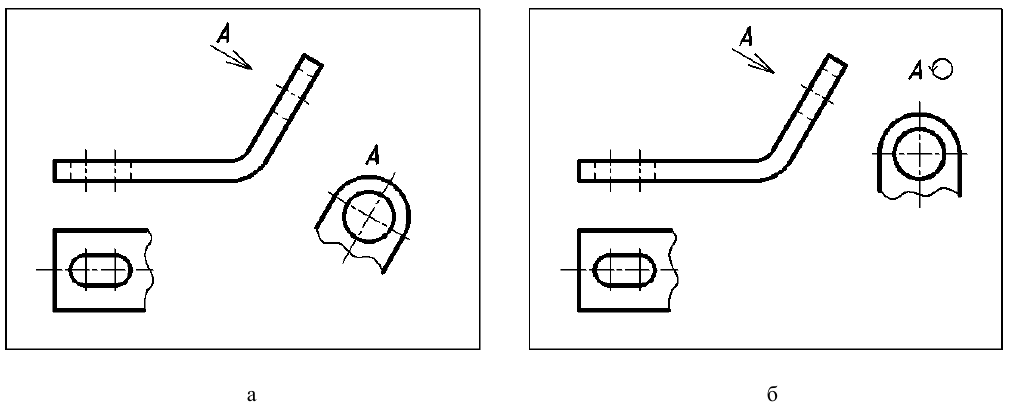
а — дополнительный вид не повернут; б — дополнительный вид повернут
Обозначение дополнительных видов
При обозначении всех видов, в том числе и дополнительных, действует одно правило: если вид не находится в проекционной связи с соответствующим изображением предмета, то он должен быть обозначен (см. рис. 11, а), если же вид находится в непосредственной проекционной связи с соответствующим изображением, то он не обозначается (рис. 12).
Дополнительный вид допускается поворачивать, но с сохранением, как правило, положения, принятого для данного предмета на главном изображении (см. рис. 11, б); при этом обозначение вида должно быть дополнено условным графическим обозначением 
Рис. 12. Пример дополнительного вида, который находится в проекционной связи с основным изображением и не обозначается
Разрезы
Основным назначением видов является определение формы внешних поверхностей предмета. Выявление на видах формы внутренних поверхностей при помощи штриховых линий не принято, так как это может привести к неправильному пониманию конструкции предмета. Поэтому для определения внутреннего строения применяют разрезы и сечения.
Разрез — это изображение предмета, мысленно рассеченного одной и более секущими плоскостями. Отсеченную часть предмета, расположенную между наблюдателем и секущей плоскостью, мысленно удаляют, в результате чего становятся видимыми контуры внутренних, ранее закрытых поверхностей. В разрезе показывают то, что лежит в секущей плоскости, и то, что расположено за ней. Невидимые контуры, которые в разрезе стали видимыми, изображают сплошной толстой линией, а фигуру, полученную в результате пересечения предмета плоскостью, заштриховывают. Штриховку выполняют по ГОСТ 2.306 — 68 [6]. Мысленное рассечение предмета относится только к данному разрезу и не влечет за собой изменения других изображений. На чертеже может быть представлено несколько разрезов предмета.
Секущие плоскости должны проходить по плоскостям симметрии предмета, по осям отверстий и пересекать полости, как правило, по их центру.
Разрезы могут быть расположены:
- на месте основных видов;
- на свободном поле чертежа.
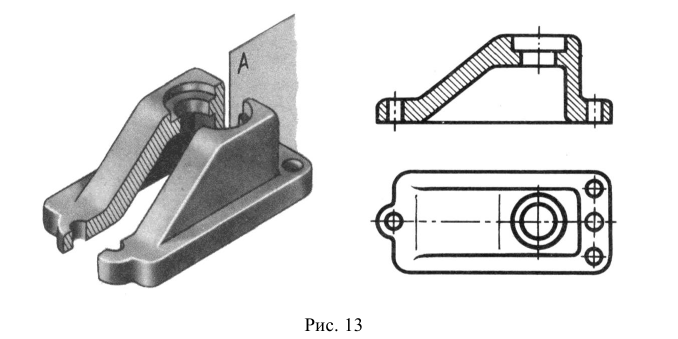
Построение разреза показано на рис. 13. Предмет рассечен секущей плоскостью, параллельной фронтальной плоскости проекций (см. рис. 13, б). На ортогональных проекциях (см. рис. 13, а) отсеченная часть предмета мысленно удалена, а оставшаяся часть изображена на месте вида спереди.
Допускается показывать невидимые поверхности на видах штриховыми линиями только тогда, когда контуры этих поверхностей являются простыми фигурами и не затемняют виды.
Допускается изображать нс все, что расположено за секущей плоскостью, если этого не требуется для понимания конструкции предмета.
Рис. 13. Образование фронтального разреза: а — ортогональные проекции; б — аксонометрическая проекция предмета
Простые разрезы
В зависимости от количества секущих плоскостей разрезы разделяются на простые и сложные. Простые разрезы получают при применении одной секущей плоскости, они легко читаются, поэтому им следует отдавать предпочтение.
В зависимости от положения секущей плоскости простой разрез может быть:
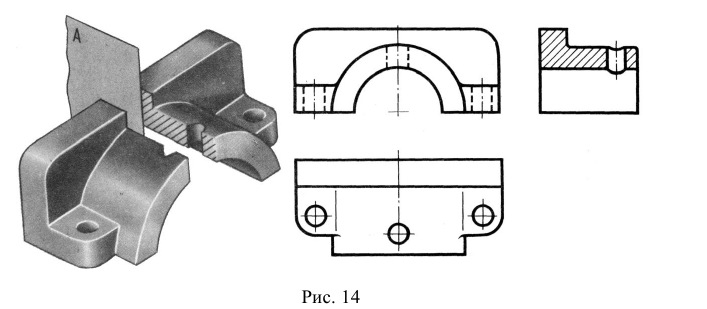
- горизонтальным — секущая плоскость параллельна горизонтальной плоскости проекций (см. рис. 14, разрез А-А).
- вертикальным — секущая плоскость перпендикулярна к горизонтальной плоскости проекций (например разрезы на рис. 13, 15);
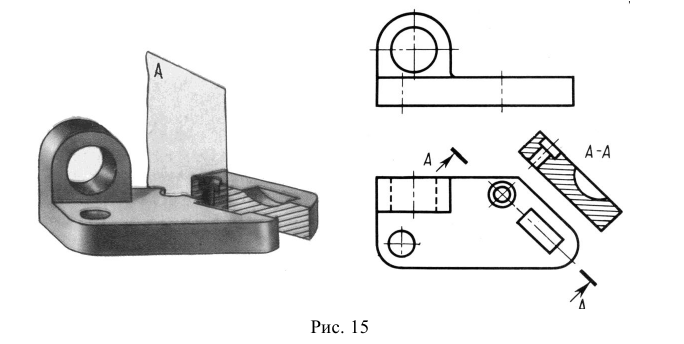
- наклони ы м — секущая плоскость составляет с горизонтальной плоскостью проекций угол, отличный от прямого (рис. 16, разрез А-А)- Допускается наклонный разрез поворачивать до ближайшего горизонтального или вертикального положения (рис. 17).
Вертикальный разрез называется фронтальным, если секущая плоскость параллельна фронтальной плоскости проекций (см. рис. 13), и профильным, если секущая плоскость параллельна профильной плоскости проекций (см. рис. 15).
Если секущая плоскость направлена вдоль длины или высоты предмета, то разрез называется продольным (рис. 18, разрез А-А). Если секущая плоскость перпендикулярна длине или высоте предмета, то разрез называют поперечным (см. рис. 18, разрез Б-Б).
Разрезы, образованные одной секущей плоскостью, но со встречным направлением взгляда наблюдателя, выполняются так, как показано на рис. 19.
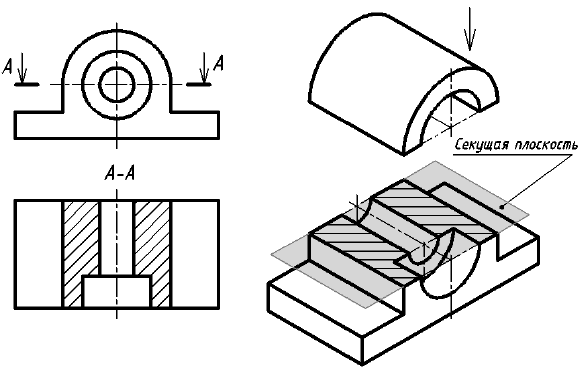
Рис. 15. Образование профильного разреза
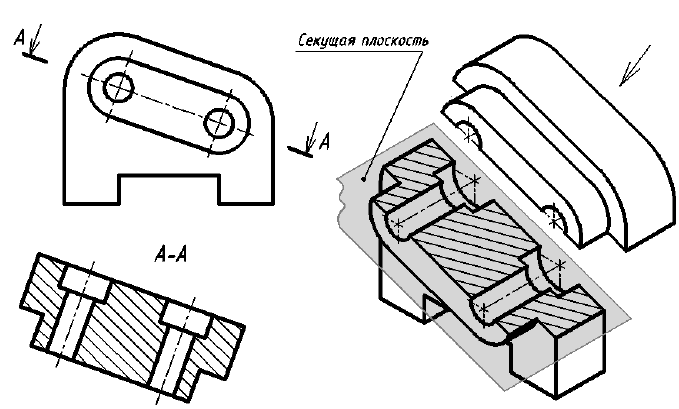
Рис. 17. Повернутый наклонный разрез 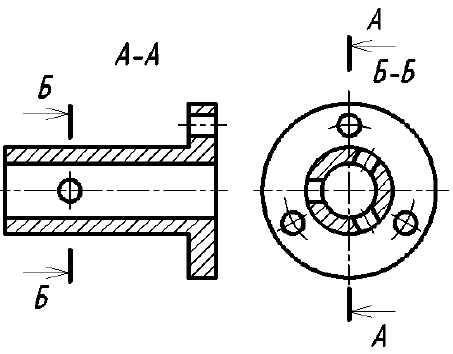
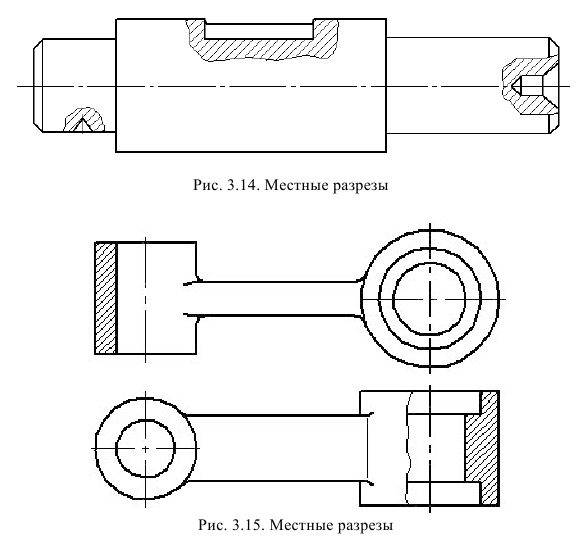
Местные разрезы
Местные разрезы представляет собой часть простого разреза (рис. 20), который располагается на виде и ограничивается сплошной волнистой линией. Местный разрез применяется для выявления внутренней формы предмета в отдельном ограниченном месте. С помощью местных разрезов показывают форму невидимых отверстий, пазов, канавок и других элементов в том случае, если они занимают по отношению к виду его малую часть и делать полный разрез нерационально. Волнистая линия, ограничивающая местный разрез, не должна совпадать с другими линиями изображения.
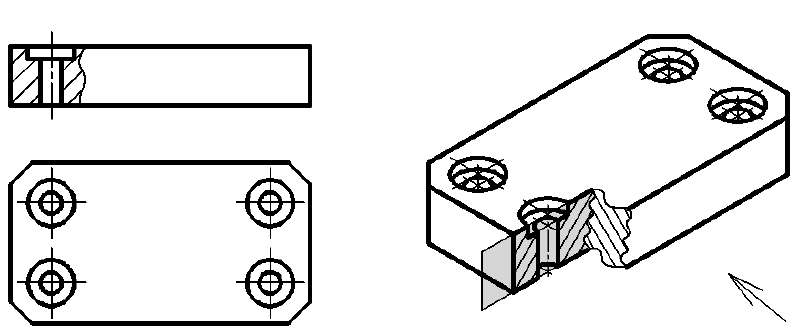
Обозначить разрез — это значит:
- показать положение секущей плоскости;
- сопроводить надписью сам разрез.
Положение секущей плоскости указывается на чертеже разомкнутой линией, причем начальный и конечный штрихи не должны пересекать контур соответствующего изображения. К начальному и конечному штрихам проводятся стрелки, указывающие направление взгляда наблюдателя. Стрелки должны располагаться на расстоянии 2 . 3 мм от наружных по отношению к «разрезаемому» изображению концов штрихов. Со стороны внешнего угла около стрелок ставится одна и та же прописная буква русского алфавита. Построенный при сечении указанной плоскостью предмета разрез должен быть отмечен надписью с применением той же буквы по типу А-А (всегда двумя буквами через тире). Пример обозначения разреза приведен на рис. 13.
Однако, как видно из рис. 13 . 20, одни разрезы на чертежах обозначены, другие не обозначены. Необходимо четко уяснить, когда разрезы обозначаются, а когда нет.
Простой разрез не обозначается, если секущая плоскость совпадает с плоскостью симметрии предмета в целом, а соответствующие изображения располагаются в непосредственной проекционной связи и не разделены какими-либо другими изображениями. Примеры таких разрезов приведены на рис. 13, 15.
Во всех остальных случаях простые горизонтальные, фронтальные и профильные разрезы должны быть обозначены.
Наклонные разрезы обозначаются всегда.
Местные разрезы не обозначаются.
Примечание. Не допускается при обозначении разреза применять ту же букву, которая была употреблена для обозначения других изображений на чертеже. По ГОСТ 2.305 — 2008 [1] для ограничения местных разрезов и в качестве линий обрыва изображений может применяться сплошная тонкая линия с изломами, начертание которой см. в ГОСТ 2.303 — 68 [4].
Структура обозначения положения секущей плоскости на чертеже показана на рис. 21. 
Стрелки, применяемые для указания направления взгляда, должны иметь такую же форму и размеры, как и стрелки для обозначения видов (см. рис. 8). Обратите внимание, что направление стрелок при обозначении положения секущей плоскости, должно соответствовать направлению взгляда при построении того вида, в границах которого полностью или частично будет располагаться разрез.
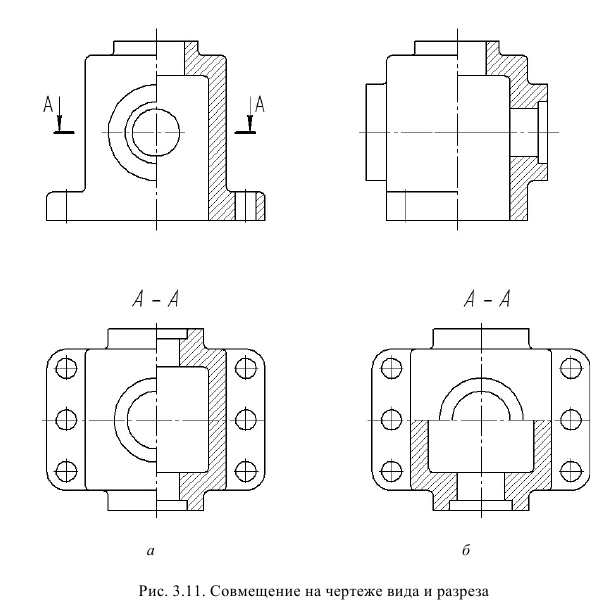
Совмещение разрезов с видами
Изображений на чертеже должно быть минимальное количество. Для уменьшения количества изображений применяется совмещение разрезов с видами. В большинстве случаев разрез совмещается с тем видом, который располагается по направлению взгляда наблюдателя на плоскости проекций, параллельно которой ориентирована секущая плоскость. Фронтальный разрез размещают на месте вида спереди или сзади (см. рис. 13), горизонтальный — на месте вида сверху или снизу (см. рис. 14), профильный — на месте вида слева или справа (см. рис. 15).
Возможны три варианта совмещения:
- в границах вида располагают полный разрез, т. е. выполняют полное совмещение разреза с соответствующим видом, как на рис. 13, 15, 18. Такое совмещение делают тогда, когда разрез представляет собой несимметричную фигуру, а на виде нет видимых контуров конструктивных элементов, форму которых нужно раскрыть;
- в границах вида располагают часть вида и часть соответствующего разреза, разделяя их сплошной волнистой линией (рис. 22). Такое совмещение выполняют тогда, когда разрез или вид представляют собой несимметричные фигуры и на виде имеются видимые контуры конструктивных элементов, форму которых нужно раскрыть (на рис. 22, для того, чтобы форма паза на передней стенке предмета была понятна, необходимо оставить видимой часть вида спереди с этим пазом). Как правило, при подобном совмещении простые разрезы не обозначают;
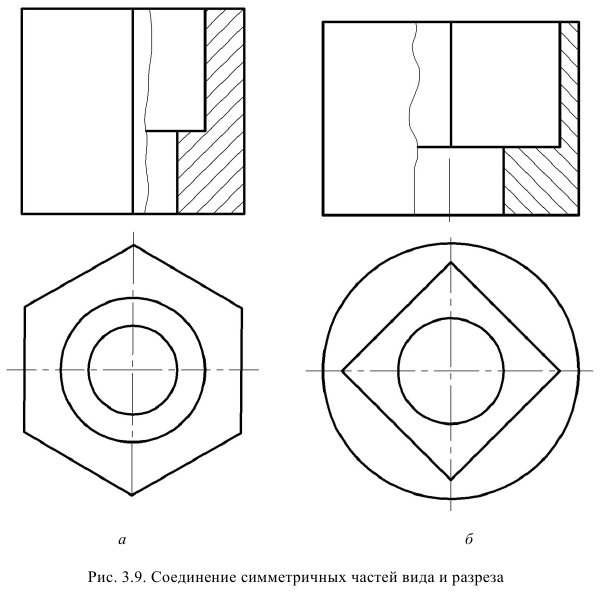
- в границах вида располагают половину вида и половину соответствующего разреза, разделяя их штрихпунктирной линией, являющейся осью симметрии вида и разреза (рис. 23). Таким образом, этот вариант совмещения можно применить, только если полный вид и полный разрез в отдельности представляют собой симметричные фигуры. Тогда по половине симметричного изображения легко понять полную форму. Вид принято располагать слева от оси симметрии, а разрез справа или вид располагать сверху, а разрез снизу. Обозначение разрезов в этом случае производится по правилу, изложенному в подразд. 4.3.
- Если совмещаются часть вида и часть соответствующего разреза или половина вида и половина разреза, то на части вида штриховые линии не проводят.
- Если при совмещении на одном изображении симметричных частей вида и разреза, какая-либо линия (например ребро) совпадает с осью симметрии, то эта линия (ребро) должна быть показана, и тогда вид от разреза отделяется сплошной волнистой линией, которая проводится левее (рис. 24, а) или правее (рис. 24, б) оси симметрии.
На рис. 13 . 16, 20 были приведены примеры с одним разрезом предметов. Для предметов сложной формы приходится выполнять несколько разрезов (рис. 18, 25 . 27), причем отдельные разрезы приходится иногда располагать вне видов на свободном поле чертежа.
Рис. 22. Совмещение несимметричных вида и разреза
Рис. 23. Совмещение симметричных вида и разреза (половины вида и половины разреза): а — разрез не обозначается; б — разрез обозначается
Рис. 24. Совмещение симметричных вида и разреза, когда ребро совпадает с осыо симметрии: а — ребро показано на разрезе; б — ребро показано на виде
Рис. 25. Выполнение разрезов на видах спереди, сверху и слева (совмещены половины видов и половины разрезов)
Рис. 26. Возможный вариант совмещения половины вида и половины разреза на изображении сверху на рис. 25
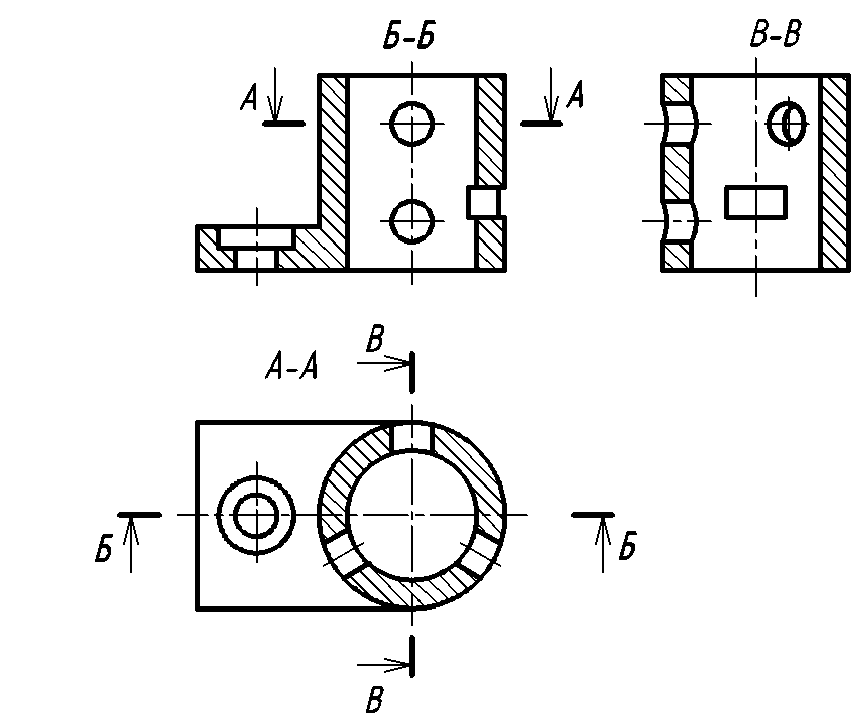
Сложные разрезы
Выявление формы внутренних полостей предметов, имеющих сложное внутреннее устройство, при помощи простых разрезов приводит к необходимости выполнять их большое количество, что затрудняет чтение чертежа. В таких случаях применяют сложные разрезы. Сложные разрезы всегда обозначают.
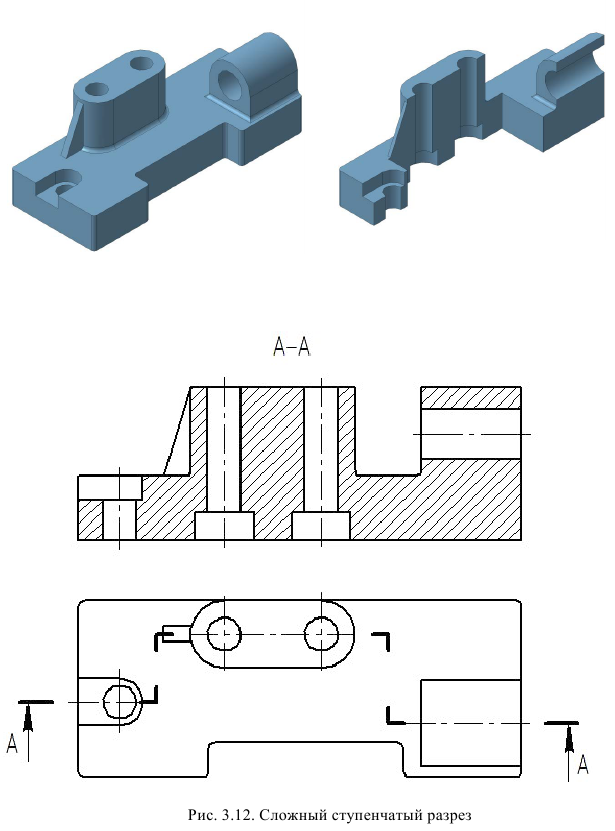
Сложным разрезом называют разрез, который получают при помощи двух и более секущих плоскостей. Сложные разрезы разделяются на ступенчатые и ломаные.
Ступенчатый разрез — это разрез, образованный несколькими параллельными секущими плоскостями (рис. 28).
При построении разреза секущие плоскости совмещают в одну, и ступенчатый разрез приобретает форму простого. Ступенчатые разрезы, так же как и простые, могут быть горизонтальными, фронтальными, профильными и наклонными (рис. 28 . 31).
Положение каждой секущей плоскости обозначают штрихами разомкнутой линии, места перехода от одной плоскости к другой (ступеньку) выполняют такими же штрихами. У начального и конечного штрихов указывают стрелкой направление взгляда наблюдателя и ставят одну и ту же букву. То есть, несмотря па то, что секущих плоскостей несколько, буквенные обозначения их одинаковы.
На ступенчатом разрезе линия перехода от одной плоскости к другой (ступенька) не изображается. На чертеже может быть несколько ступенчатых разрезов.
Примечание. Правая плоскость (см. рис. 28) может пересекать как нижнее, так и верхнее квадратное отверстие.
Рис. 28. Образование фронтального ступенчатого разреза.
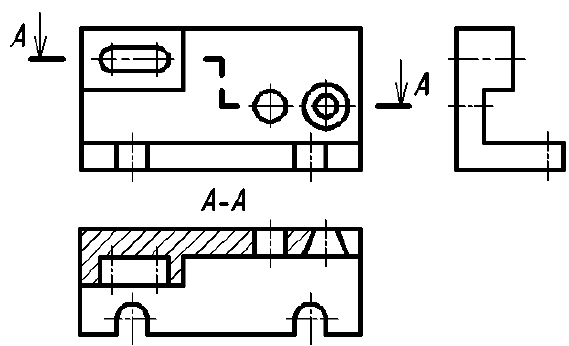
Рис. 30. Профильный ступенчатый разрез
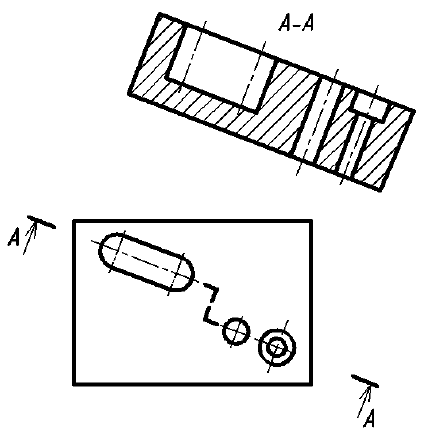
Для симметричных предметов рекомендуется рассекать их плоскостями так, чтобы полный ступенчатый разрез стал симметричной фигурой, что позволит соединить половину вида и половину разреза (рис. 32).
Не следует стремиться выявлять все внутреннее строение предмета одним сложным разрезом. Для образования ступенчатого разреза рекомендуется применять не более трех секущих плоскостей.
Рис. 32. Совмещение половины ступенчатого разреза с половиной вида спереди
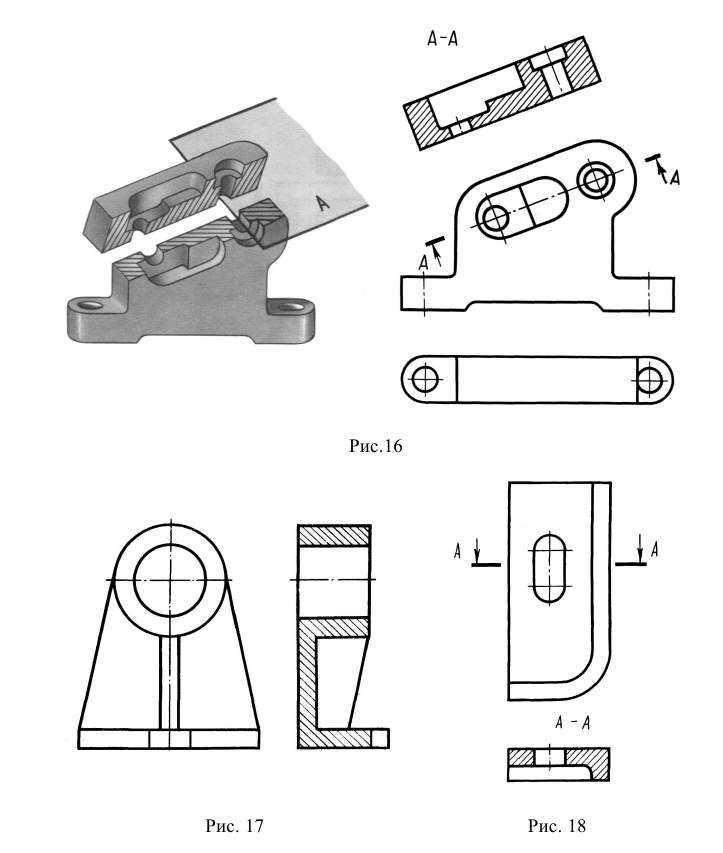
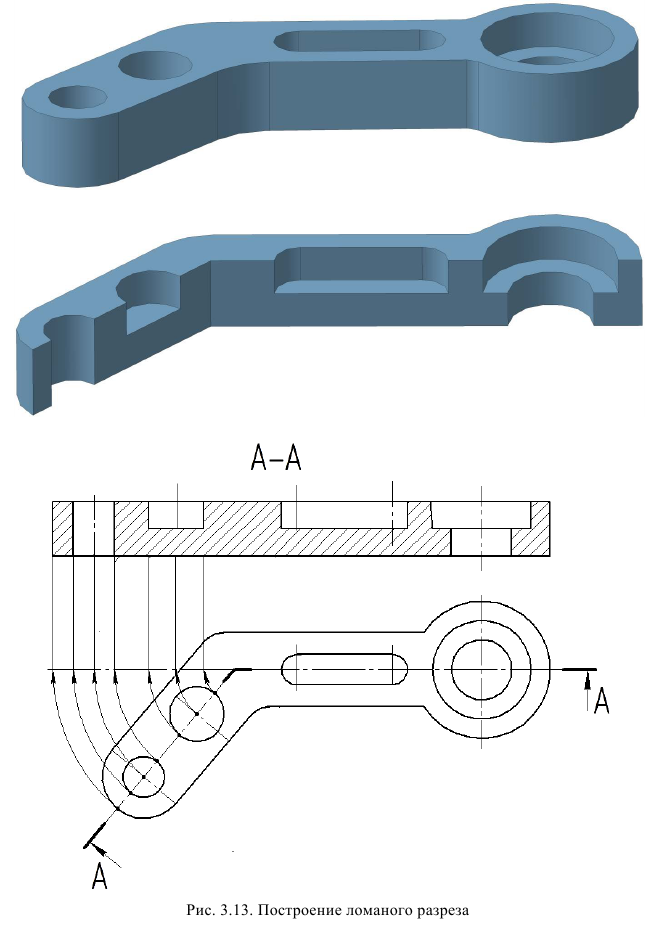
Ломаный разрез — это разрез, образованный двумя пересекающимися секущими плоскостями (рис. 33). Первая секущая плоскость выбирается параллельной, а вторая наклонной по отношению к основной плоскости проекций. При выполнении ломаного разреза наклонную секущую плоскость условно поворачивают до совмещения с первой секущей плоскостью, и из этого положения осуществляется проецирование получившейся фигуры сечения на параллельную ей плоскость проекций. При повороте наклонной секущей плоскости элементы предмета, видимые за ней, поворачивать не нужно, а следует строить их изображение в прямой проекционной связи с той плоскостью проекций, на которую производится проецирование. Подобным образом построен на верху цилиндрического выступа предмета (см. рис. 33) прямоугольный паз, который не связан с наклонной секущей плоскостью. Исключением из этого правила является вариант, когда видимые элементы конструктивно связаны с рассекаемым элементом. В подобном случае эти видимые за секущей плоскостью элементы поворачиваются вместе с рассекаемым элементом (рис. 34).
Ломаные разрезы в зависимости от того, на какой плоскости проекций (на каком виде) они будут располагаться, делятся на фронтальные, горизонтальные и профильные.
Положение каждой секущей плоскости обозначают штрихами разомкнутой линии. В месте пересечения секущих плоскостей также ставятся такие штрихи. У начального и конечного штрихов указывают стрелкой направление взгляда наблюдателя и ставят одну и ту же букву. Обратите внимание, что буква у наклонного штриха независимо от наклона плоскости изображается прямо.
Примечание. На рис. 33 наклонная секущая плоскость может пересекать как нижнее, так и верхнее отверстия. Построение ломаного разреза и в том, и в другом случае будет одинаковым.
Рис. 33. Образование фронтального ломаного разреза
Рис. 34. Проецирование элементов, конструктивно связанных с наклонной секущей плоскостью
Сечения
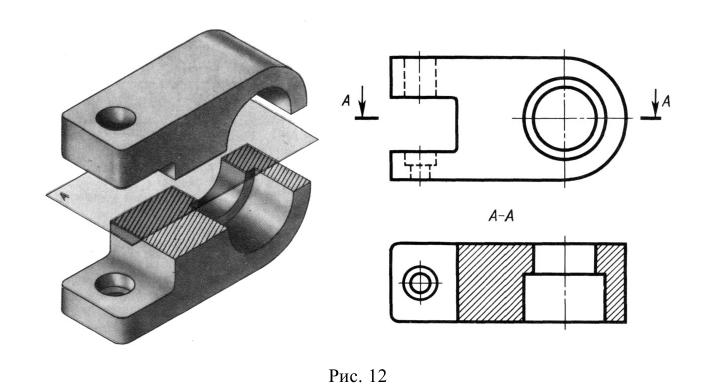
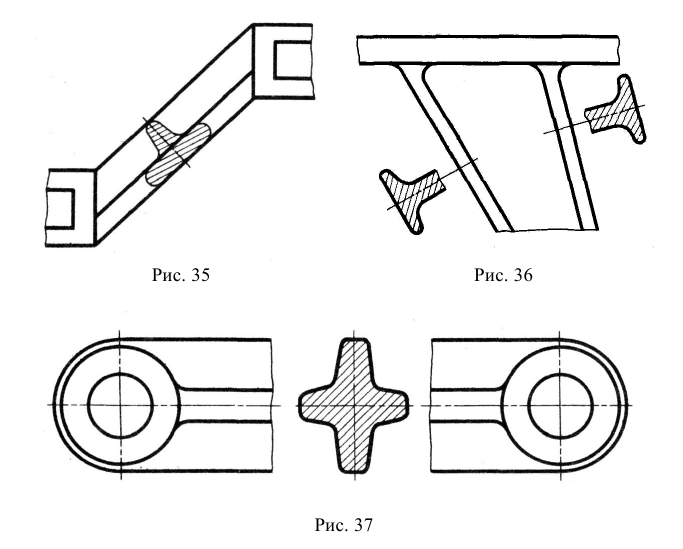
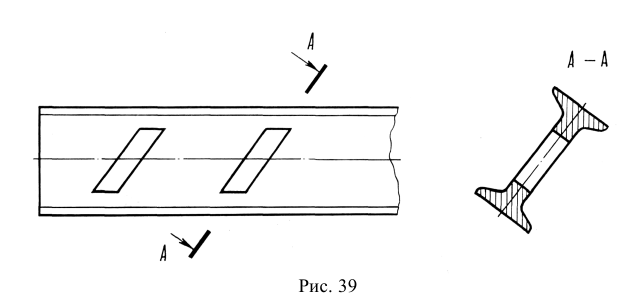
Сечением называется изображение, которое получается при мысленном рассечении предмета плоскостью. В отличие от разреза на сечении показывают только то, что расположено непосредственно в секущей плоскости. На рис. 35 показано отличие сечения от разреза.
Сечения применяются для выявления формы отдельных элементов предмета в тех случаях, когда на разрезе определяемые контуры нужного элемента затемняются изображениями других элементов второго плана. 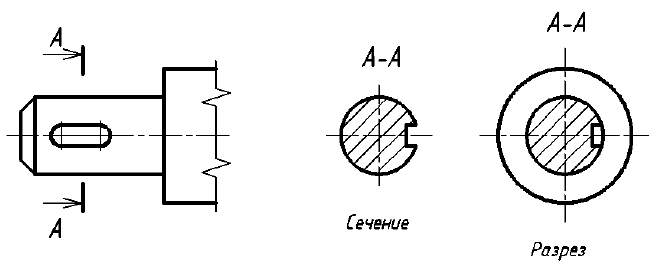
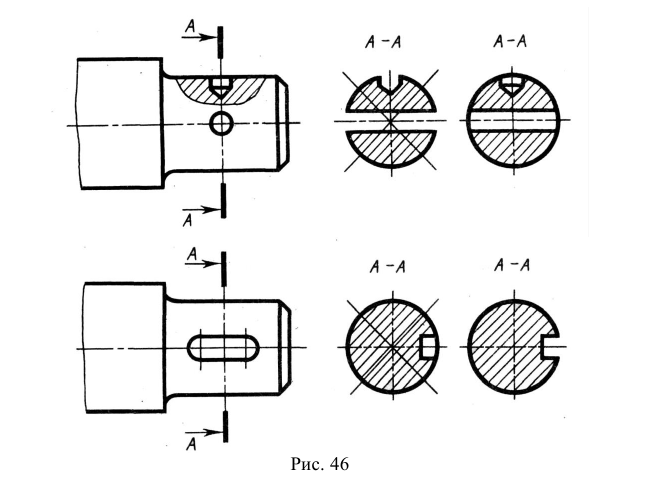
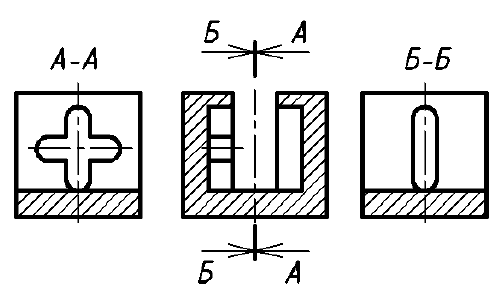
При выполнении сечений следует руководствоваться следующим правилом: фигура сечения должна представлять собой замкнутый контур. Не допускается сечение в виде разомкнутых частей. Так, если для пояснения формы паза на рис. 35 целесообразнее выполнить сечение, то для пояснения сквозного овального отверстия на рис. 36 следует выполнять разрез.
Рис. 36. Иллюстрация правильного и неправильного выявления формы отверстия на изображениях А-А
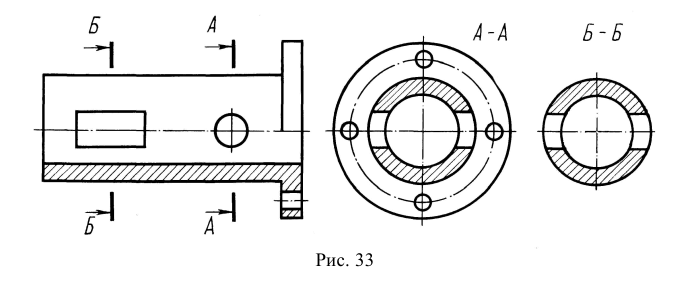
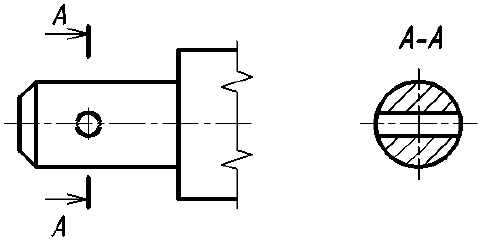
Однако существует исключение из приведенного выше правила: если секущая плоскость проходит по оси вращения круглого отверстия, то в сечении показывают полный контур этого отверстия, т. е. показывают и линии заднего плана, относящиеся к данному отверстию (рис. 37).
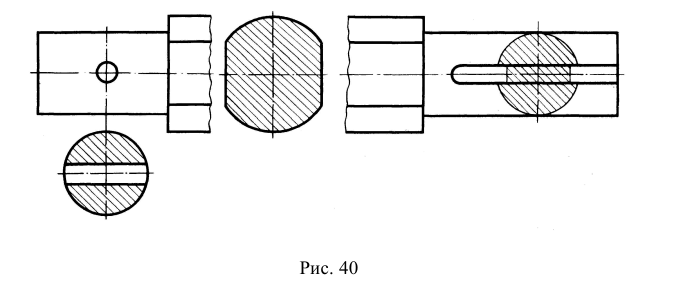
Сечения разделяют на входящие в состав разреза и не входящие в состав разреза (см. рис. 35, где видно, что сечение полностью входит в состав разреза).
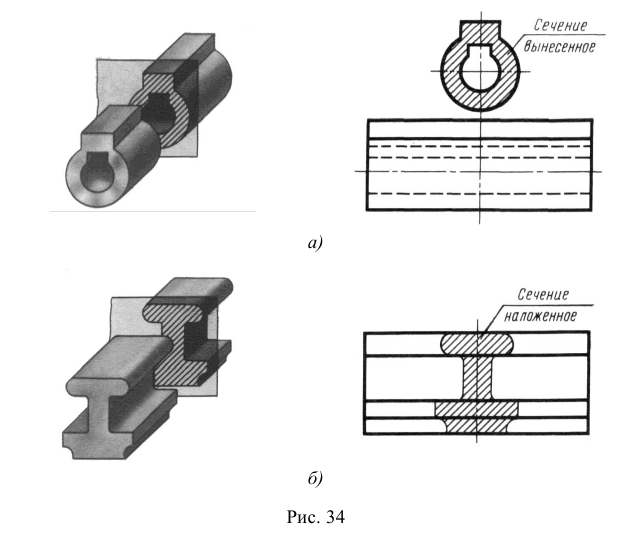
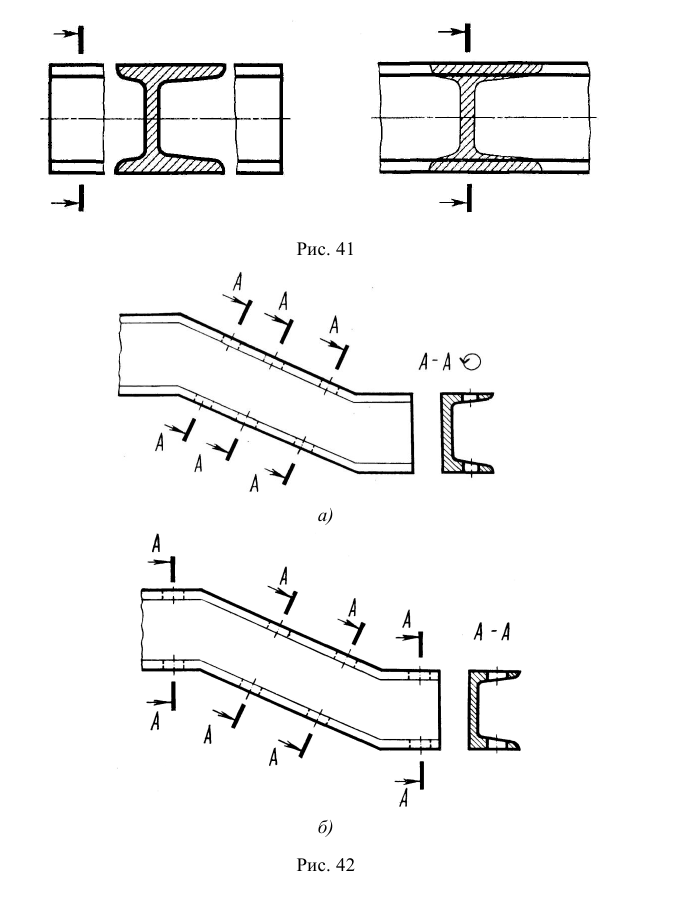
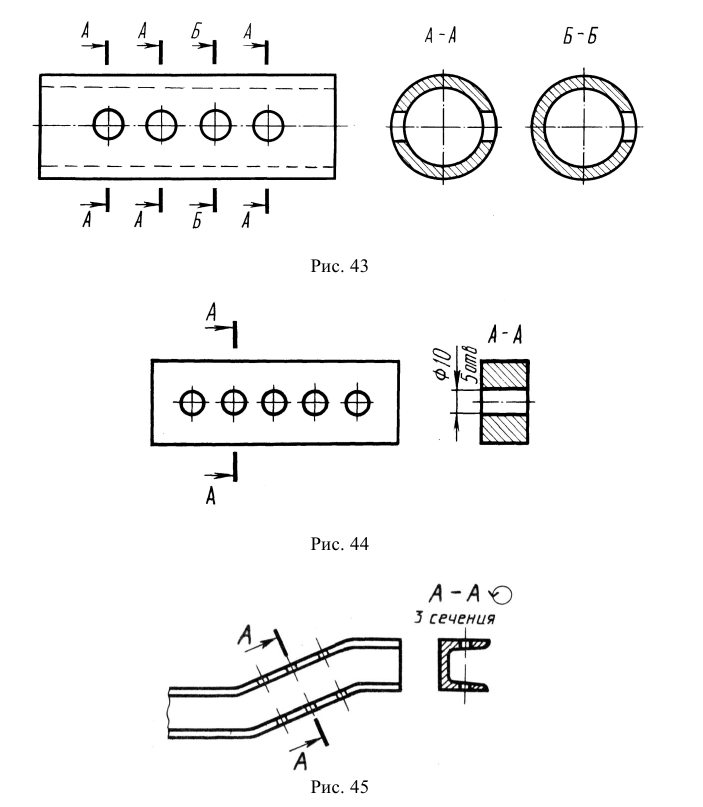
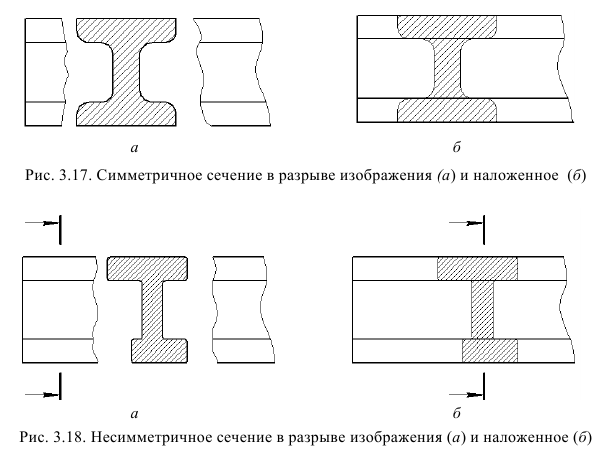
Классификация сечений дана на рис. 38, 39. Сечения, не входящие в состав разреза, по месту своего расположения разделяются на вынесенные и наложенные. Контур вынесенного сечения обводится сплошной толстой линией, контур наложенного — сплошной тонкой. И вынесенные, и наложенные сечения могут быть симметричными и несимметричными.
Вынесенным называется сечение, которое размещено вне основных изображений предмета. Вынесенное сечение может располагаться:
- на свободном поле чертежа в любом удобном месте. Такое сечение должно быть обозначено (см. рис. 38, а, б);
- в разрыве вида. При этом, если сечение симметрично, то оно не обозначается (см. рис. 38, в); если несимметрично, то оно должно быть обозначено указанием положения секущей плоскости и направления взгляда наблюдателя без буквенных обозначений (см. рис. 38, г);
- на продолжении следа секущей плоскости. Так могут быть выполнены только симметричные сечения, и они не обозначаются (см. рис. 38, д).
Наложенным называется сечение, которое располагается па виде предмета. Если наложенное сечение имеет симметричную форму, то в качестве линии секущей плоскости выступает ось симметрии сечения (см. рис. 39, а). Если наложенное сечение несимметрично, то оно должно быть обозначено указанием положения секущей плоскости и направления взгляда наблюдателя без буквенных обозначений (см. рис. 39, б).
Рис. 38. Вынесенные сечения

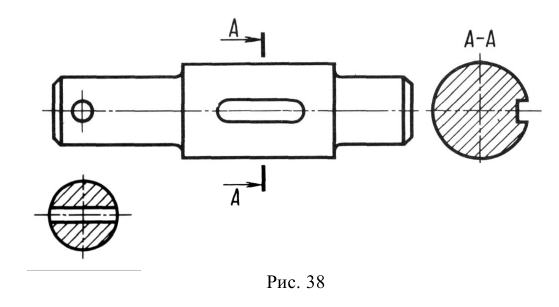
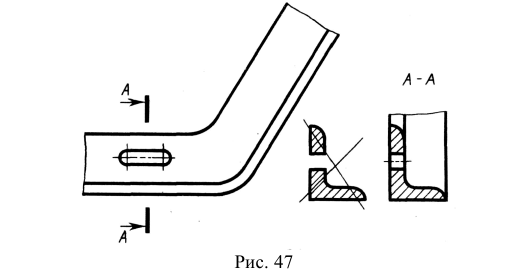
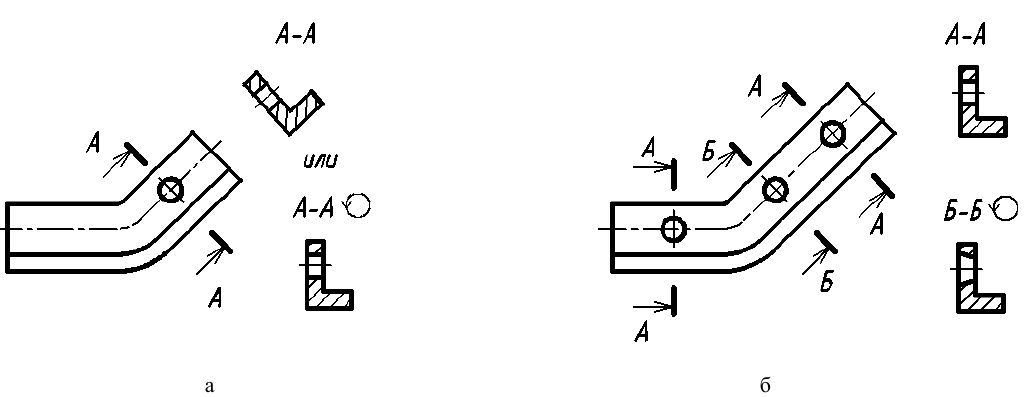
Сечение наклонного участка предмета по построению и расположению должно соответствовать направлению, указанному стрелками; допускается такое сечение поворачивать с добавлением условного графического обозначения 
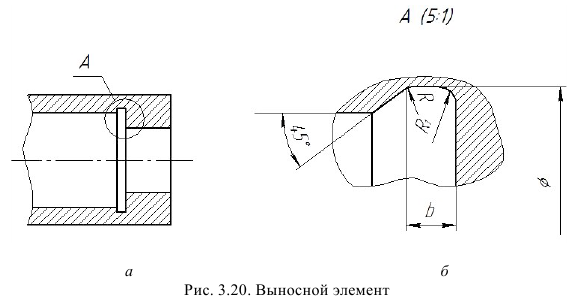
Выносные элементы
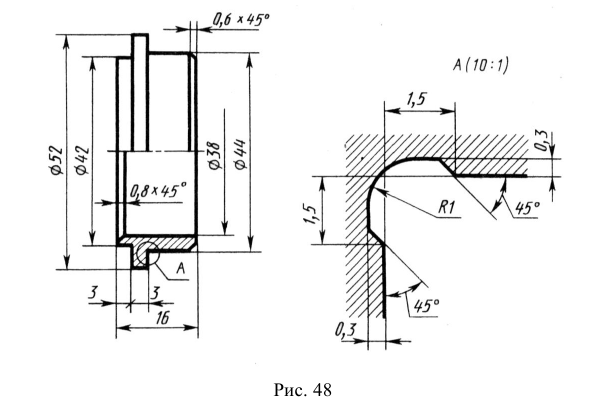
Выносной элемент — это дополнительное отдельное изображение какой-либо части предмета (рис. 41), которое выполняется с целью уточнения ее формы и размеров. Как правило, выносной элемент вычерчивается в более крупном масштабе (см. рис. 41, а, б). Выносной элемент может отличаться от соответствующего исходного изображения и по содержанию, т. е. исходное изображение может быть видом, а выносной элемент разрезом (см. рис. 41, б). Рекомендуется выносной элемент вычерчивать на свободном поле чертежа как можно ближе к исходному изображению.
При выполнении выносного элемента необходимо тонкой сплошной линией обвести на исходном изображении геометрической фигурой (чаще окружностью или овалом) часть предмета, требующую пояснений. От этой фигуры проводят линию-выноску, на полке которой указывают буквенное обозначение выносного элемента. Эту же букву с указанием в скобках масштаба увеличения наносят над выносным элементом.
Рис. 41. Выносные элементы
Условности и упрощения на чертежах
Для уменьшения трудоемкости выполнения чертежей ГОСТ 2.305 — 2008 [1] предусматривает следующие условности и упрощения, которые могут быть применены при выполнении заданий проекционного черчения:
1. Если вид, разрез или сечение представляет симметричную фигуру, то допускается вычерчивать половину симметричного изображения (рис. 42, вид слева) или немного более половины с проведением в последнем случае линии обрыва (рис. 42, вид сверху).
Рис. 42. Выполнение части симметричного изображения
2. Допускается упрощенно изображать линии пересечения поверхностей вращения, если не требуется их точного построения. Например, вместо геометрически точно построенных кривых можно проводить дуги окружностей или прямые (рис. 43, а, б). Однако если пересекаются поверхности вращения, описанные около условной сферы, линиями пересечения которых являются прямые, то эти прямые необходимо показывать (рис. 44).
Рис. 43. Упрощенное изображение линий пересечения поверхностей вращения
Рис. 44. Изображение линий пересечения поверхностей вращения с одинаковым диаметром
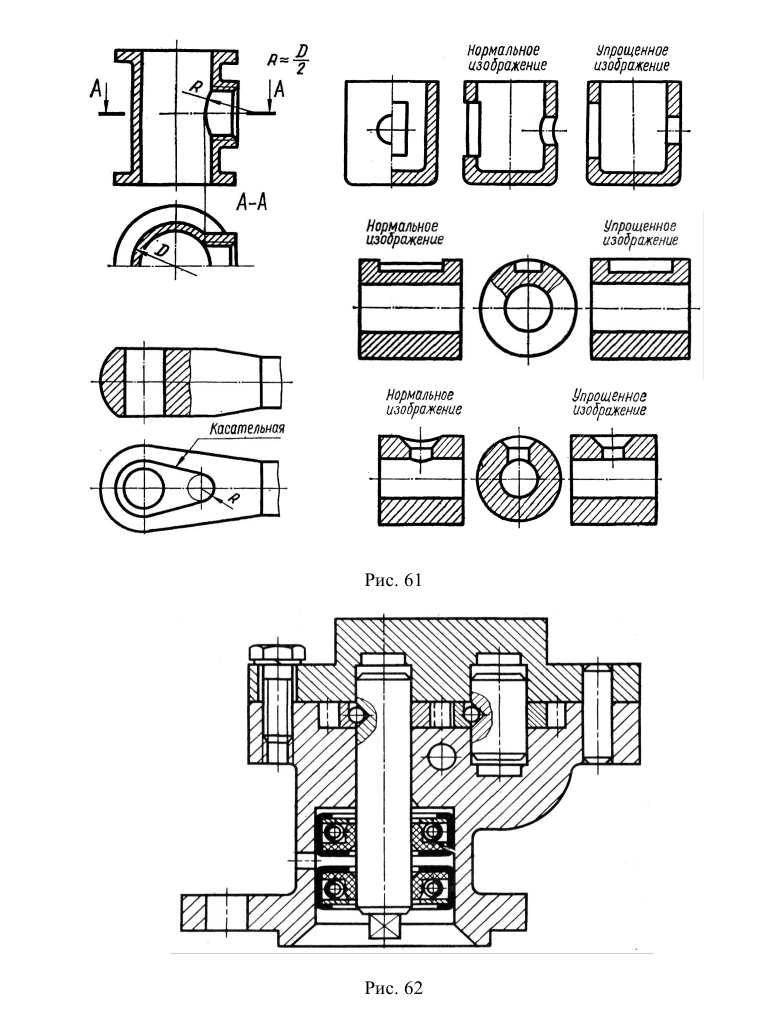
3. Плавный переход одной поверхности в другую показывают условно тонкой линией (рис. 45, а) или вообще не показывают (рис. 45, б).

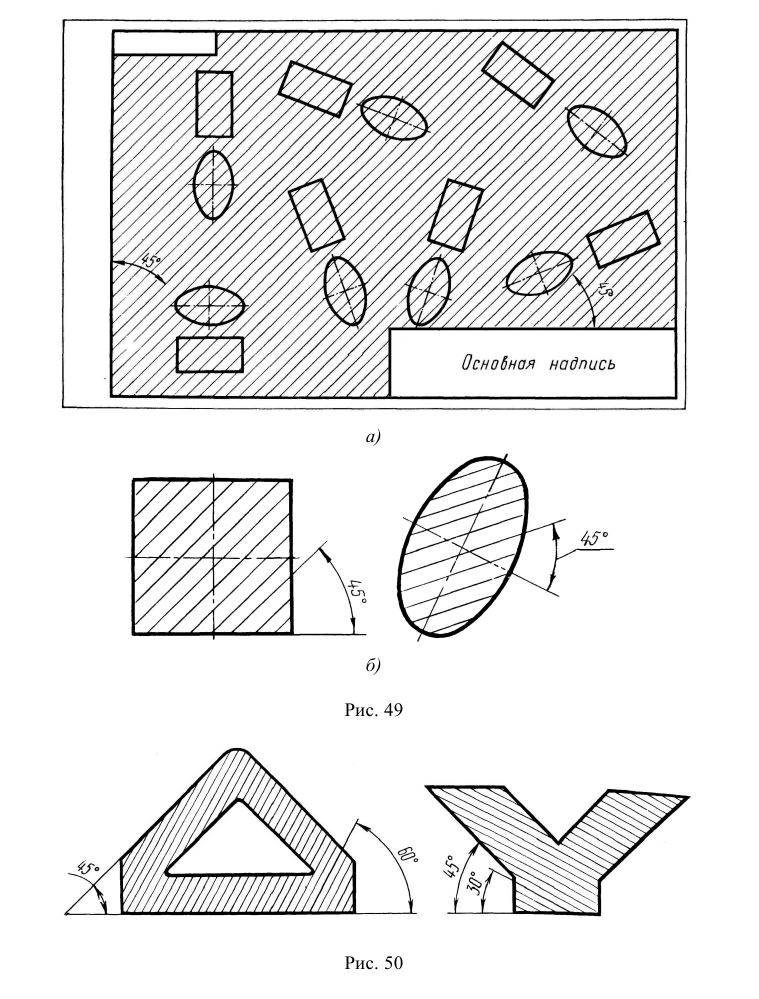
4. Плоские участки поверхности допускается выделять диагоналями, проводимыми тонкими линиями (рис. 46). Как правило, такое выделение выполняют, если плоские поверхности находятся на цилиндрических поверхностях или соседствуют с ними.
Рис. 46. Пример выделения плоских участков поверхностей диагональными линиями
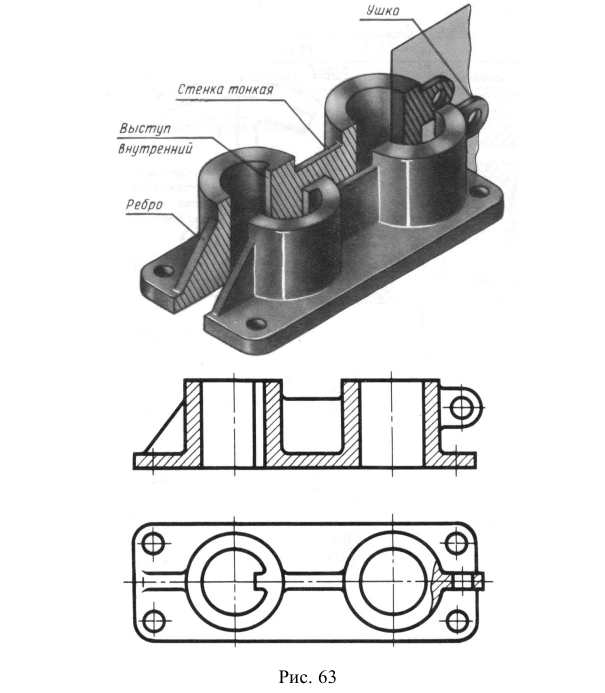
5. Если секущая плоскость рассекает тонкую стенку параллельно большей грани, то ее условно показывают нерассеченной, отделяя от остальной части предмета основной линией (рис. 47, фронтальный разрез), и не штрихуют. В поперечных разрезах тонкие стенки изображают рассеченными и заштриховывают по общим правилам (рис. 47, разрез А-А). Если в тонкой стенке имеются отверстия, то их следует показывать местными разрезами (см. рис. 47, местный разрез на левом ребре жесткости).
Примечание. Тонкими стенками в техническом черчении называют конструктивные элементы (как правило ребра жесткости), у которых одна грань явно больше других.
Рис. 47. Изображение тонких стенок на разрезах
6. Если предмет имеет несколько одинаковых равномерно расположенных элементов, то на изображении этого предмета полностью показывают один такой элемент, а положение остальных задают условно, например центровыми линиями. На рис. 48 продублирован вид сверху предмета, изображенного на рис. 47, но уже с условным обозначением отверстий.
Рис. 48. Условное изображение одинаковых отверстий
7. Допускается на разрезах не показывать элементы, видимые за секущей плоскостью, если форма этих элементов уже выявлена. Особенно это касается элементов, которые видны на заднем плане под углом и проецируются с искажением формы. Так, на рис. 49 три одинаковых ребра жесткости. Однозначно определена форма правого ребра, поэтому в левой части разреза ребро на заднем плане не показано.
Рис. 49. Пример разреза, на котором левое ребро не изображается
Нанесение размеров
Предметы обладают формой и величиной. Форму предмета на чертеже передают изображения. Величину предмета определяют размеры. ГОСТ 2.307 — 68 [8] устанавливает правила нанесения размеров. Ниже приведены правила, знание которых необходимо при выполнении заданий проекционного черчения.
Размеры на чертеже наносятся один раз без повторения.
Различают размеры линейные (рис. 50, а) и угловые (рис. 50, б). Линейные размеры указывают в миллиметрах, а угловые — в градусах.
Размеры наносят при помощи размерных чисел, размерных и выносных линий (см. рис. 50, а). Размерные числа должны отражать действительные размеры изображаемого предмета независимо от того, в каком масштабе выполнены изображения.
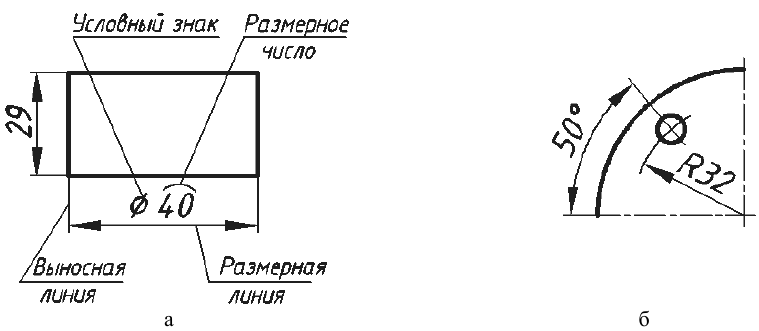
Рекомендуемое начертание размеров на чертежах показано на рис. 51.
Размерная линия — это линия, которая с двух сторон ограничена размерными стрелками. Опа в два — три раза тоньше основной линии на чертеже. Первая размерная линия должна отстоять от линии видимого контура изображения минимум па 10 мм, расстояние между параллельными размерными линиями минимум 7 мм. Не допускается использовать в качестве размерных линий линии контура, выносные, осевые и центровые. Необходимо избегать пересечения размерных линий между собой и с другими линиями чертежа.
Размерное число (рекомендуемый размер шрифта 5 мм) проставляют над размерной линией с зазором 1 . 1,5 мм. Размерное число наносят приблизительно на середине размерной линии. На параллельных размерных линиях размерные числа проставляют в шахматном порядке со сдвигом на 1 . 3 цифры относительно друг друга. Размерные числа не допускается пересекать или разделять любыми линиями чертежа.
Выносные линии (они выполняются в два — три раза тоньше основной линии), начинаются в опорных точках изображений и должны выходить за концы стрелок размерных линий на 1 . 5 мм.
Размерные стрелки должны иметь форму и размеры, показанные на рис. 52. Рекомендуемая длина стрелок — 5 или 7 мм. При компьютерном исполнении чертежа допускается в стрелках применять угол 30°.
Рис. 51. Начертание размеров
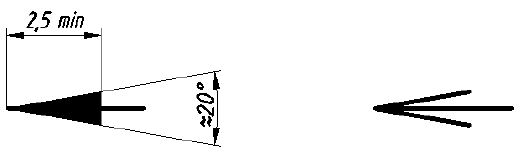
При нанесении размера окружности перед размерным числом размещают знак диаметра, перед размером дуги — знак радиуса (рис. 53).
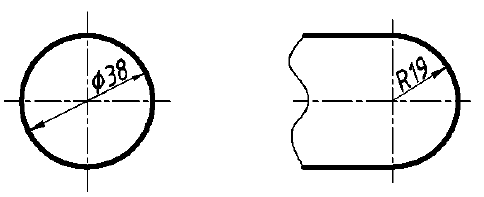
При нехватке места размерные стрелки и размерные числа наносят на продолжении размерных линий (рис. 54).
Рис. 54. Варианты нанесения размерных чисел и стрелок размерных линий Размеры узких последовательно расположенных участков наносят так, как показано на рис. 55.
Рис. 55. Варианты нанесения размеров в узких местах
При выполнении чертежа всегда приходится задаваться вопросом, на каком изображении предпочтительнее нанести тот или иной размер. ГОСТ 2.307 — 68 [8] дает следующие рекомендации:
1. Размеры, определяющие форму элемента предмета, наносят на том изображении, на котором эта форма видна и понятна (рис. 56, а). В данном случае только на виде сверху видно, что отверстие имеет прямоугольную форму и именно здесь, а не на разрезе необходимо нанести размеры формы отверстия (размеры 15 и 9). Исключением из общего правила являются круглые отверстия, размеры диаметров которых наносят предпочтительно на их разрезах и сечениях (рис. 56, б; размер 
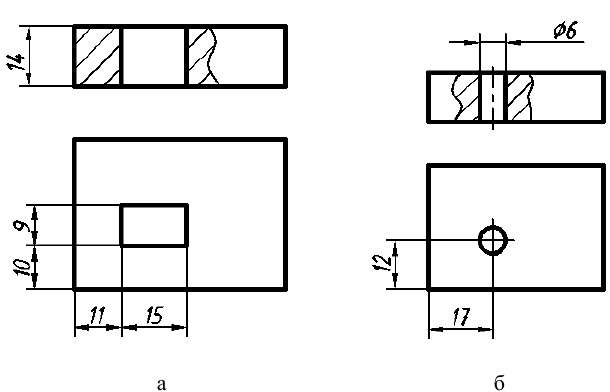
2. Размеры положения элемента относительно других поверхностей предмета наносят на виде, т. е. на том изображении, где можно произвести два измерения (см. рис. 56, а; размеры 10 и 11 и рис. 56, б; размеры 12, 17). Помните, что положение круглого отверстия или выступа задаются координатами только его центра.
3. Размеры наружных и внутренних элементов по возможности следует располагать по разные стороны изображения (рис. 57). Не следует наносить размер расстояния между наружной и внутренней поверхностями (см., например, зачеркнутый размер 7 на рис. 57).
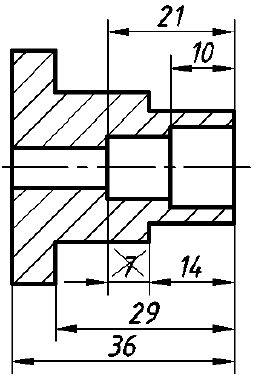
4. Размеры одинаковых круглых отверстий как простой, так и сложной формы наносят один раз с указанием их количества (рис. 58, а). Для отверстий допускается только следующая структура записи: 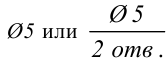
Рис. 58. Пример нанесения размеров одинаковых круглых отверстий: а — простой формы; б — сложной формы
5. Размеры симметрично расположенных элементов наносят так, как нанесен размер 24 на рис. 59, а. Если же имеется только половина симметричного изображения, то все равно должен быть указан его полный размер. В этом случае размерную линию проводят с обрывом, и обрыв размерной линии делают несколько дальше оси симметрии (см. рис. 59, б; размеры 24 и 34).
Рис. 59. Пример нанесения размеров симметрично расположенных элементов
Аксонометрические проекции предметов
На технических чертежах изделие изображается в виде ортогональных проекций (видов, разрезов, сечений). Недостатком ортогональных проекций является то, что они не дают непосредственного представления о форме изображенного предмета. Так, каждый основной вид представляет собой точное отображение только одной грани. Чтобы представить по этим видам полную форму предмета, необходимо иметь соответствующие навыки.
Для наглядного объемного представления о предмете применяют аксонометрические проекции по ГОСТ 2.317 — 69 [9], которые позволяют одним изображением передать общую форму предмета.
Аксонометрическая проекция — это проекция предмета на одну плоскость, относительно которой ни одна грань предмета в форме параллелепипеда не расположена параллельно или перпендикулярно. При таком проецировании видны три грани предмета (искаженные), и изображение получается наглядным. В общем случае для предметов любой формы, в том числе и круглых, для построения аксонометрического изображения предмет проецируют на некоторую плоскость вместе с осями прямоугольных координат X, Y и Z, к которым предмет отнесен в пространстве. Направление взгляда при этом не должно совпадать с направлениями координатных осей.
Аксонометрическое изображение дает общее наглядное представление о форме предмета, но не передает точно действительную форму и размеры поверхностей.
Если направление проецирования перпендикулярно к плоскости проекций, то на этой плоскости получают прямоугольную аксонометрическую проекцию (рис. 60, а), если не перпендикулярно -то косоугольную (рис. 60, б).
Для использования в учебной практике рекомендуются два вида аксонометрических проекций — прямоугольная изометрическая и косоугольная фронтальная диметрическая.
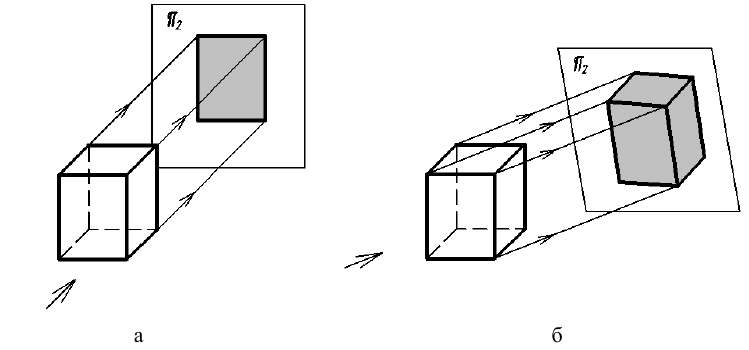
Прямоугольная изометрическая проекция
Прямоугольной изометрической проекцией (прямоугольной изометрией) называется аксонометрическая проекция, у которой углы между аксонометрическими осями равны 120°, а коэффициенты искажения по всем трем осям равны единице (рис. 61).
Прямоугольные грани, проецируются в виде параллелограммов, а окружности, лежащие на этих гранях проецируются в виде эллипсов. На рис. 62 показано изображение куба и окружностей на его гранях в прямоугольной изометрии. Построение эллипсов заменяется в учебном курсе более простым построением овалов, которое приведено на рис. 63. Эллипсы в каждой грани строятся одинаково.
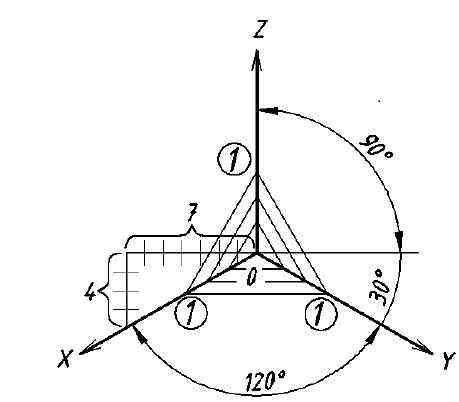
Рис. 62. Изображение куба и окружностей на его гранях в прямоугольной изометрии
Построение эллипсов. Построим эллипс на верхней грани куба.
- Этап 1 (рис. 63, а). Наметим на грани центр эллипса — точку
Проведем через нее изометрические оси X и Y (они параллельны сторонам верхней грани). Отложим в обе стороны от точки
на каждой оси отрезки, равные радиусу окружности. Через полученные точки проведем прямые, параллельные осям. Получим ромб, представляющий изометрическую проекцию квадрата, в который вписана окружность.
- Этап 2 (рис. 63, б). Из вершины ромба в точке А проведем отрезок АВ и, взяв его в качестве радиуса Rt, построим верхнюю дугу. Аналогично построим нижнюю дугу (на рисунке она не показана).
- Этап 3 (рис. 63, в). На пересечении отрезка АВ с горизонтальной осью ромба определим точку С, из которой проведем правую дугу радиусом R2, равным отрезку СВ. Так же построим левую дугу, которая на рисунке не показана.
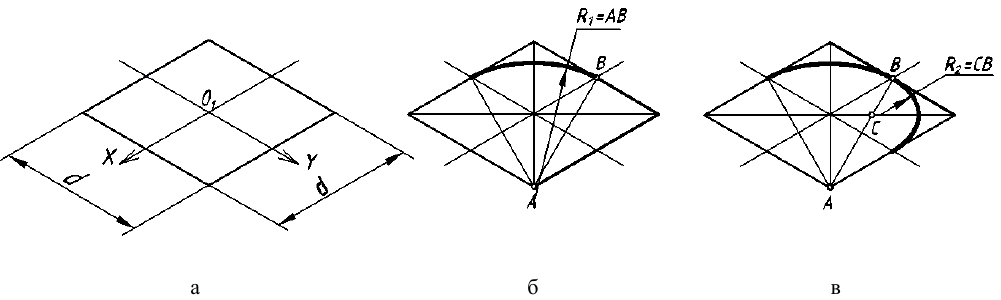
Косоугольная фронтальная диметрическая проекция
Косоугольной фронтальной диметрической проекцией (фронтальной диметрией) называется аксонометрическая проекция, у которой углы между аксонометрическими осями располагаются так, как показано па рис. 64. Коэффициенты искажения по осям Хи Z равны единице, а по оси Y- 0,5.
Особенностью этого вида аксонометрии является то, что грань, параллельная координатной плоскости X0Z, и находящаяся на ней окружность проецируются без искажений (рис. 65). Две другие видимые грани и окружности на них проецируются с искажениями: грани в виде равновеликих параллелограммов, а окружности в виде равновеликих эллипсов, причем большие оси этих эллипсов равны l,06d, а малые — 0,35d (d — диаметр исходной окружности). Построение упрощенных эллипсов как овалов показано на рис. 66.
Рис. 64. Расположение аксонометрических осей в косоугольной фронтальной диметрии
Рис. 65. Изображение куба и окружностей на его гранях Построение эллипсов. Построим эллипс, например, на верхней грани куба в плоскости X0Y (см. рис. 66).
- Этап 1. Наметим в плоскости X0Y центр эллипса — точку 0/. Проведем через нее горизонтальную и вертикальную оси; под углом 7° 14′ к этим осям построим прямые, задающие направления осей эллипса. На этих прямых отложим большую (отрезок
и малую (отрезок
оси эллипса с центром в точке
- Этап 2. Отложим в обе стороны от точки
на продолжениях оси
отрезки, равные диаметру исходной окружности d и определим точки
на рис. 66 не показана). Из точек
и
проведем дуги радиусом R =
- Этап 3. На пересечении отрезка
с большой осью эллипса
определим точку
из которой радиусом
проведем левую дугу. Аналогично построим правую дугу.
Подобным образом на грани Z0Y построим эллипс с центром в точке 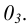
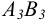
В плоскости X0Z построим окружность без искажения ее формы и размера с центром в точке
Рис. 66. Построение эллипсов во фронтальной диметрии
Разрезы в аксонометрических проекциях
В аксонометрических проекциях предметов для показа внутренней конфигурации, как правило, выполняют разрезы двумя и более взаимно перпендикулярными секущими плоскостями, параллельными координатным плоскостям X0Z, Y0Z или X0Y. Эти разрезы образуют вырез, на котором видно внутреннее строение предмета. Если предмет имеет две плоскости симметрии (вид сверху симметричен относительно двух осей), то обычно выполняют так называемый «четвертной вырез», при котором секущие плоскости совпадают с плоскостями симметрии (рис. 67). В предметах с одной плоскостью симметрии или несимметричных секущие плоскости должны проходить по осям отверстий и центрам полостей любой формы (рис. 68). Разрезы на ортогональных изображениях чертежа могут не совпадать с разрезами в аксонометрических проекциях. Линии штриховки сечений наносят параллельно одной из диагоналей проекций квадратов, построенных в соответствующих координатных плоскостях (см. рис. 61, 64). Штриховка пересекающихся сечений должна быть встречной. Ниже приведены примеры аксонометрических изображений предметов с «вырезами» (рис. 67, 68).
Рис. 67. Прямоугольная изометрическая проекция с «четвертным вырезом» 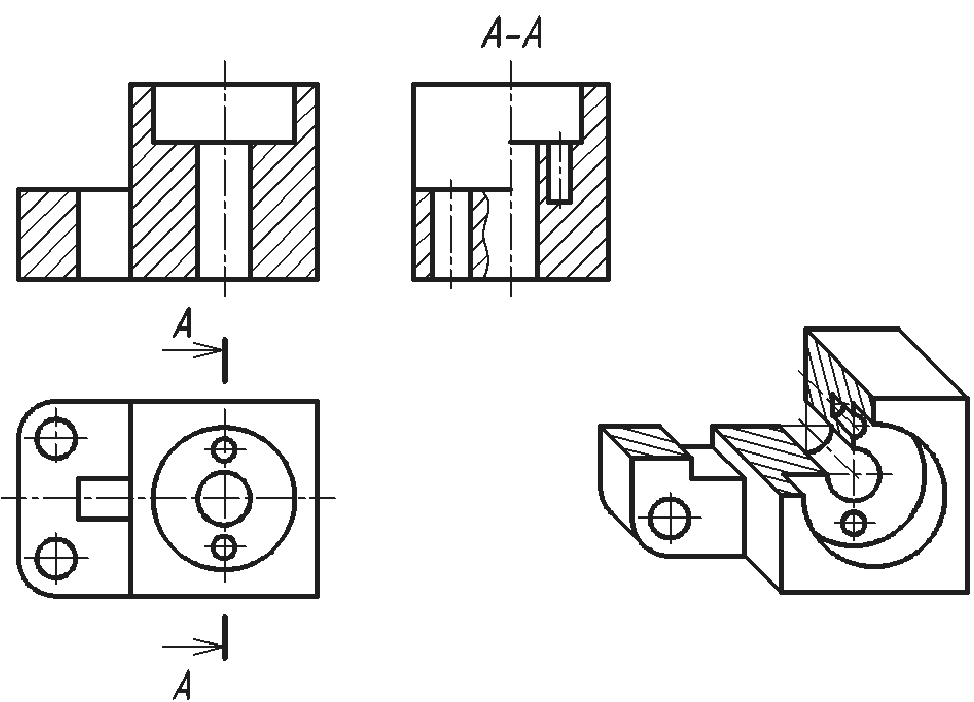
Выбор вида аксонометрии
Для изображения одного и того же предмета могут быть выбраны различные виды аксонометрии из разрешенных к применению ГОСТ 2.317 — 69 [9].
Как показала учебная практика, наиболее наглядной и понятной для студентов является прямоугольная изометрическая проекция, в которой предмет изображается в таком же положении, в каком он расположен на чертеже на виде спереди (см. рис. 67).
С точки зрения уменьшения трудоемкости чертежа рекомендуется:
- прямоугольную изометрию применять тогда, когда круглые отверстия и выступы располагаются на соседних гранях предмета, как на рис. 67;
- фронтальную диметрию применять тогда, когда подобные элементы находятся только на одной или на двух противоположных параллельных гранях предмета, как на рис. 68. Предмет в аксонометрии располагать так, чтобы грань с наибольшим количеством окружностей и дуг была параллельна плоскости проекций X0Z, при этом окружности и кривые изображаются без искажений.
Построение действительной формы сечения
В учебной практике широко распространены задачи на построение действительной величины сечения, образованного наклонной секущей плоскостью. Такие задачи хорошо развивают пространственное воображение.
Как правило, заданная секущая плоскость является проецирующей. Наиболее удобным способом построения действительной формы сечения является способ замены плоскостей проекций, который подробно изучается в курсе начертательной геометрии.
На рис. 69 показано построение действительной формы сечения предмета наклонной плоскостью А-А.
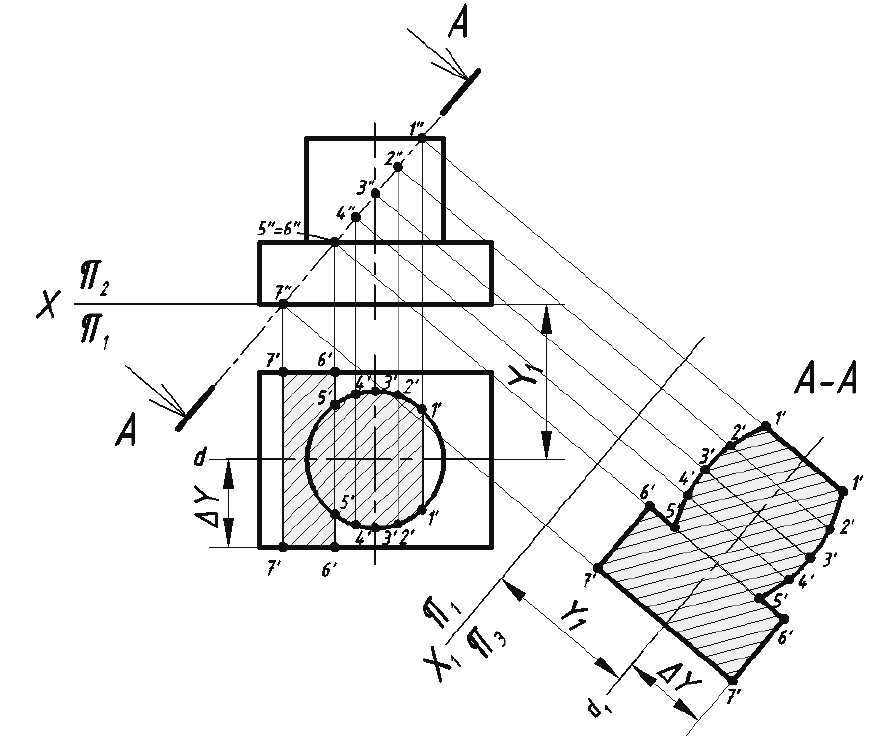
Показанный на рис. 69 предмет состоит из двух простых тел: параллелепипеда в основании и расположенного на нем цилиндра. Секущая плоскость А-А расположена под углом к оси вращения цилиндра и пересекает его боковую поверхность по эллипсу, а верхнее и нижнее основание — по прямым. Призматическое основание данная секущая плоскость пересекает по прямоугольнику. Горизонтальная проекция фигуры сечения, расположенная на виде сверху, представляет собой совмещение части эллипса с прямоугольником. Это искаженная проекция, так как при взгляде сверху фигура сечения видна под углом. Для построения действительной формы сечения по направлению взгляда, указанному стрелками секущей плоскости А-А, рекомендуется:
- провести на свободном месте чертежа на произвольном удобном расстоянии от линии сечения А-А параллельную ей ось
- на новой плоскости проекций
провести ось симметрии
на расстоянии
Это расстояние должно быть равно такому же
от оси симметрии d до оси проекций X (см. рис. 69, вид сверху);
- для удобства дальнейших построений соединить тонкой штрихпунктирной линией штрихи в обозначении положения секущей плоскости А-А (это допускается стандартом);
- на главном изображении (см. рис. 69, вид спереди) выделить опорные и промежуточные точки 1″ . 7″ сечения, затем построить их горизонтальные проекции 1′ . 7′;
- провести от точек 1″ . 7″ линии проекционной связи, перпендикулярные к оси
- на виде сверху для каждой симметричной точки 1′ . 7′ измерить ее расстояние от оси симметрии d (см. рис. 69, отрезок
и отложить эти расстояния на линиях проекционной связи в обе стороны от оси
на плоскости
Отметить построенные точки;
- соединить указанные точки кривыми и прямыми линиями и заштриховать построенную фигуру сечения. Если при этом наклон линий штриховки совпадает с направлением линий контура сечения или его осевой линии, то тогда штриховать сечение необходимо так, как показано в прил. 2 на рис. П.2.8.
Примечание. Построенное таким образом сечение можно при необходимости переместить в другое место и даже повернуть. Пример повернутого сечения см. на рис. 38, а, б.
Задачи проекционного черчения с решением
Задача 1.
По заданным двум основным видам (рис. П.1.1) построить третий вид предмета, выполнить необходимые разрезы и построить аксонометрическую проекцию (на формате АЗ).
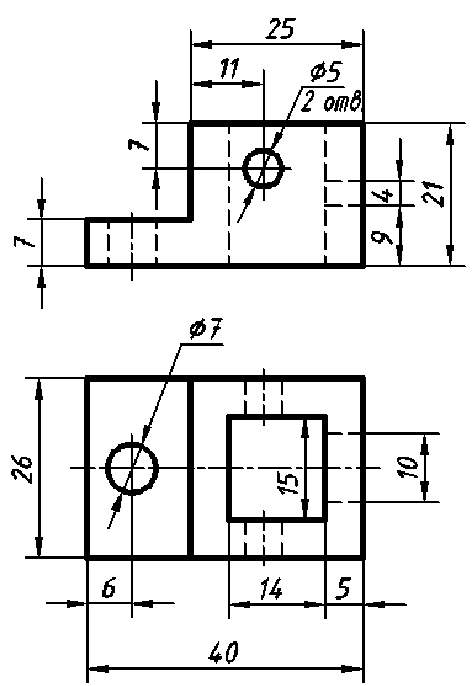
Рекомендуемая последовательность решения:
- Подготовить формат АЗ с упрощенной основной надписью.
- Перечертить заданные изображения предмета.
- Построить третье изображение — вид слева (рис. П.1.2). Для чего можно применить вспомогательную ось р или дуги окружностей с центром в точке 0.
- Построить необходимые разрезы. Для того чтобы невидимые поверхности, показанные штриховыми линиями, стали видимыми, применим три разреза (см. разд. 4):
- простой фронтальный разрез по плоскости симметрии предмета, который полностью совместим с видом спереди, так как и вид, и разрез представляют собой несимметричные фигуры. Этот разрез не обозначается (см. подразд. 4.3);
- сложный ступенчатый горизонтальный разрез А-А, который расположим на месте вида сверху, причем в силу их симметрии совместим половину вида с половиной разреза;
- простой профильный разрез Б-Б. Его расположим на месте вида слева и опять же в силу симметричности вида и разреза совместим их половины.
Построенные разрезы (рис. П.1.3) полностью выявят и сделают понятным внутреннее строение данного предмета.
Рис. П.1.2. Пример построения вида слева
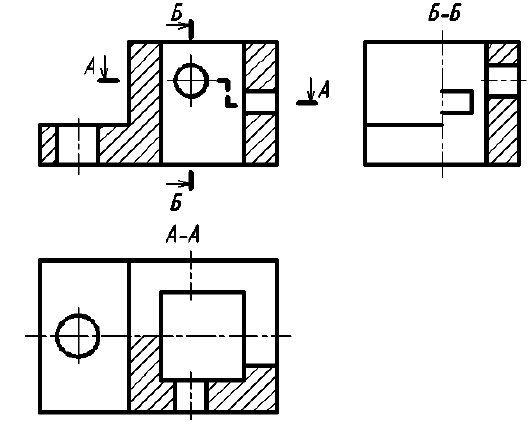
5. Построить аксонометрическую проекцию. Согласно рекомендациям по выбору вида аксонометрической проекции (см. подразд. 10.4) для данного предмета, у которого отверстия располагаются на всех гранях, целесообразнее построить прямоугольную изометрическую проекцию.
Этапы выполнения отражены на рис. П.1.4:
- построить аксонометрические оси X, У, Z. Воспользовавшись размерами, приведенными в задании (см. рис. П.1.1), выполнить изображение пластины, лежащей в основании предмета (рис. П. 1.4, а);
- построить изометрическую проекцию параллелепипеда, который расположен на пластине, и прямоугольное отверстие в нем (рис. П.1.4, б);
- по заданным размерам наметить центры круглых отверстий и выполнить их изометрические изображения — эллипсы (рис. П.1.4, в);
- определить секущие плоскости, которые позволят показать на аксонометрическом изображении внутреннюю структуру предмета. Плоскости, образующие «вырез», изображены на рис. П. 1.4, г толстой линией;
- построить «вырез» в предмете указанными секущими плоскостями (рис. П.1.4, д). Достроить отверстия, которые частично станут видны в «вырезе»;
- произвести обводку нужных линий, выполнить штриховку и удалить лишние линии. Построенная изометрическая проекция предмета показана на рис. П.1.4, е.
Рис. П.1.4. Этапы построения изометрической проекции
6. Нанести размеры, заполнить основную надпись. Полностью оформленный чертеж предмета представлен на рис. П.1.5. В обозначении чертежа ГУИР. 111814.009 первая цифра 1 обозначает номер темы, вторая цифра 1 — номер факультета, число 18 — номер кафедры, число 14 — номер рабочего места студента и число 009 — номер задания.
Рис. П.1.5. Пример выполнения проекционной задачи 1
Задача 2.
По заданным двум основным видам построить третий вид предмета, выполнить необходимые разрезы и построить действительную форму вынесенного сечения (рис. П.1.6).
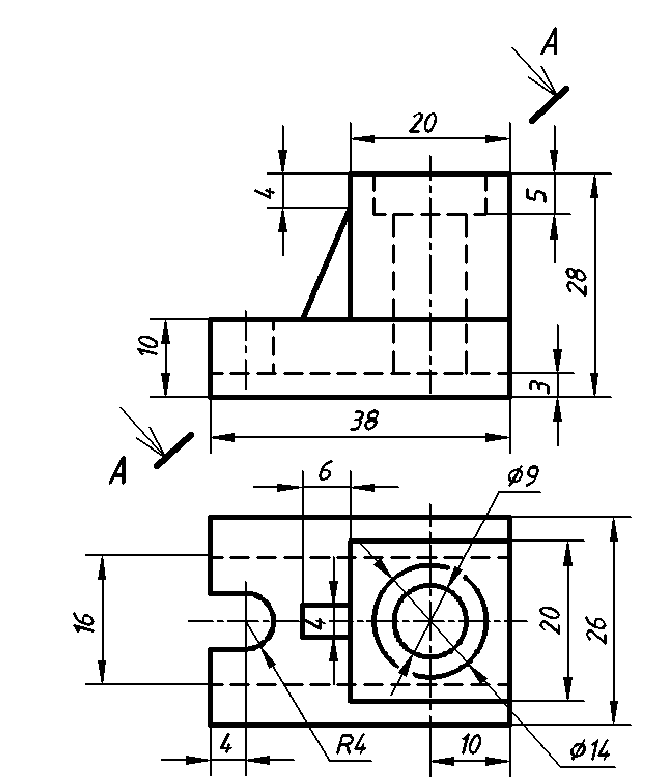
Рекомендуемая последовательность решения:
- Подготовить формат АЗ с упрощенной основной надписью.
- Перечертить заданные изображения предмета.
- Построить третье изображение — вид слева (рис. П. 1.7).
- Построить необходимые разрезы. Анализ конструкции предмета показывает, что для определения формы внутренних отверстий и паза достаточно выполнить простой фронтальный разрез по плоскости симметрии предмета. Разрез полностью совместим с видом спереди. Обратите внимание на то, как изображается в продольном разрезе ребро жесткости (см. разд. 8 рис. 46).
- Построить действительную форму сечения предмета плоскостью А-А. Методика построения рассмотрена в подразд. 10.5.
- Если это необходимо, то произвести корректировку компоновки изображений. При нехватке места следует иметь в виду, что допускается поворачивать сечение А-А до вертикального или горизонтального положения, а также выполнять половину любого, кроме главного, симметричного изображения (см. разд. 8, рис. 41).
- Произвести обводку нужных линий и удалить лишние.
- Выполнить штриховку сечения.
- Нанести размеры, заполнить основную надпись.
Полностью оформленный чертеж предмета представлен на рис. П.1.7. Обозначение чертежа производится по той же схеме, что и в задаче 1.
Рис. П.1.7. Пример выполнения проекционной задачи 2
Выдержки из стандартов по оформлению чертежей
ГОСТ 2.301 — 68. Форматы
Чертежи выполняют на листах бумаги определенного размера (формата).
Подготовленный для работы формат листа имеет вид, показанный на рис. П.2.1, и включает:
- внешнюю рамку, выполненную сплошной тонкой линией;
- внутреннюю рамку, которая проводится сплошной толстой линией на расстоянии 5 мм от правой, нижней и верхней стороны внешней рамки и на расстоянии 20 мм слева (это поле для подшивки чертежа);
- основную надпись (угловой штамп).
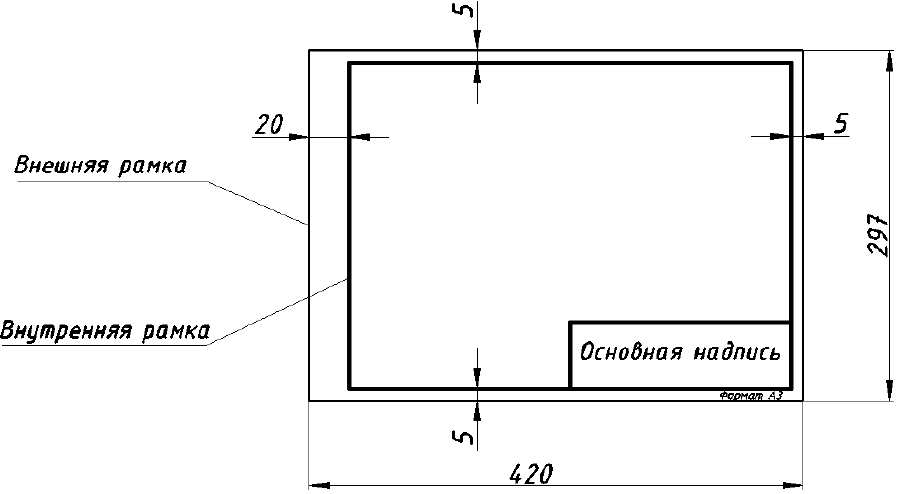
Формат листа определяется размерами сторон внешней рамки (см. на рис. П.2.1 размеры 420 и 297).
Форматы подразделяются на основные и дополнительные. Размеры и обозначения основных форматов приведены в табл. П.2.1.
Размеры основных форматов
Основную надпись чертежа выполняют по ГОСТ 2.104 — 2006 [7] и помещают в правом нижнем углу формата. На формате А4 ее располагают только вдоль короткой стороны листа, а на других форматах основная надпись может располагаться как вдоль короткой, так и вдоль длинной стороны листа.
ГОСТ 2.302 — 68. Масштабы
Масштабом называется отношение линейных размеров изображения предмета на чертеже к его действительным размерам.
Предметы следует изображать на чертеже предпочтительно в натуральную величину, так как такое изображение дает представление о действительных размерах и соотношениях сторон. Однако это не всегда возможно, и большие предметы изображают уменьшенными, а маленькие — увеличенными, что позволяет выполнять на стандартных форматах чертежи предметов практически любой величины.
Масштабы изображений на чертежах должны выбираться из следующих рядов: натуральная величина -1:1;
- масштабы уменьшения -1:2 1:2,5 1:4 1:5 1:10 1:15 и др;
- масштабы увеличения -2:1 2,5:1 4:1 5:1 10:1 20:1 и др.
Масштаб чертежа указывается в основной надписи в специально предназначенной для этого графе по типу 1:1 (рис. П.2.2). Если отдельное изображение на чертеже выполнено в масштабе, отличающемся от указанного в основной надписи, то этот масштаб записывают в скобках вслед за буквенным обозначением данного изображения. Подобным образом обозначен масштаб выносного элемента А на рис. П.2.2 (см. обозначение А(4:1)).
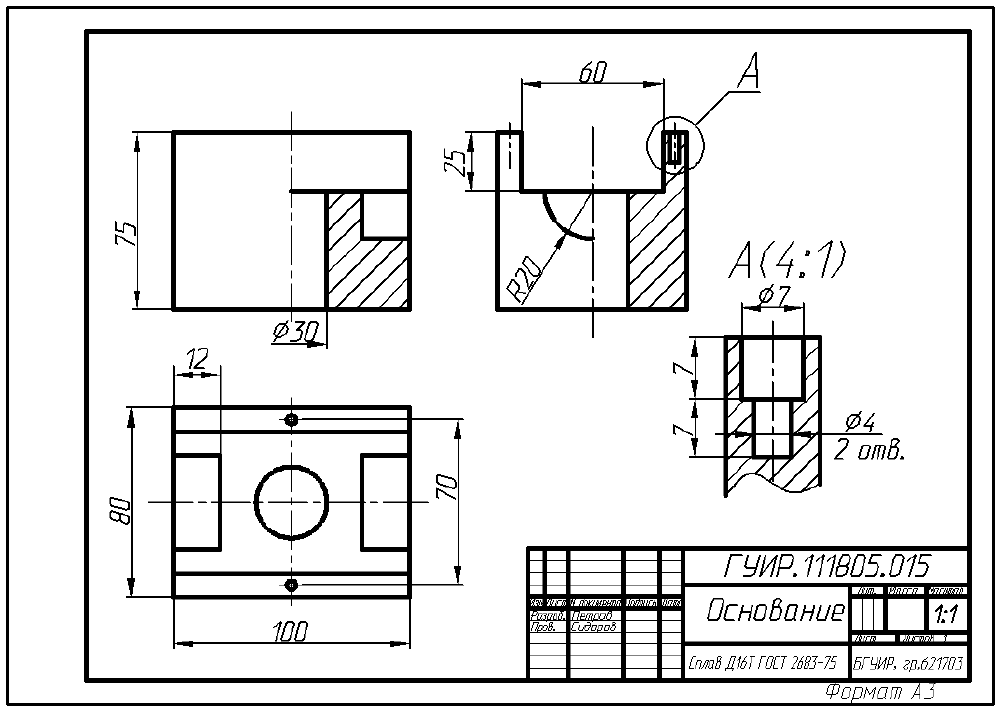
ГОСТ 2.303 — 68. Линии
Изображения на чертежах для большей их выразительности и наглядности выполняются линиями разного начертания и толщины. Установлены девять типов линий, которые представлены в табл. П.2.2. За исходную принята сплошная толстая основная линия. Ее толщина s должна быть в пределах от 0,5 до 1,4 мм в зависимости от величины и сложности изображения. Толщины остальных линий указываются отношением их к толщине основной.
Типы линий
При выполнении изображений на чертеже указанными линиями необходимо выполнять следующие требования:
- толщина линий каждого типа должна быть одинаковой для всех изображений на данном чертеже;
- штриховые и штрихпунктирные линии должны начинаться и заканчиваться штрихами;
- в центре окружностей должны пересекаться штрихи центровых штрихпунктирных линий (рис. П.2.3, а);
- если диаметр окружности в изображении (т. е. при вычерчивании ее на чертеже независимо от действительного размера) получился меньше 12 мм, то центровые штрихпунктирные линии следует заменять сплошными тонкими (рис. П.2.3, б).
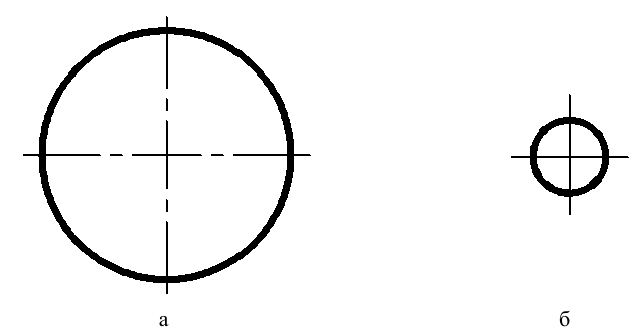
ГОСТ 2.304 — 81. Шрифты чертежные
Текстовую часть чертежей составляют надписи, числа и специальные знаки. Надписи должны быть выполнены стандартными чертежными шрифтами русского, латинского греческого алфавитов, а числа — арабскими и римскими цифрами. Шрифт каждого алфавита включает прописные (заглавные) и строчные (последующие) буквы.
Размер шрифта определяется высотой (h) прописных букв в миллиметрах. Установлены следующие его размеры: 2,5; 3,5; 5; 7; 10; 14; 20; 28; 40.
В зависимости от толщины линий обводки букв (d) различают два типа шрифта:
- тип А с толщиной линии d = l/14h;
- тип Б с толщиной линий d = l/10h.
Оба типа шрифта выполняют с наклоном 75° или без наклона (прямой шрифт).
Для построения букв, цифр и знаков применяется вспомогательная сетка, шаг линий которой равен толщине линий шрифта (d). На рис. П.2.4 показано вписывание в такую сетку букв шрифта типа А с наклоном. Следует иметь в виду, что надписи на чертежах необходимо выполнять с применением первой прописной буквы и последующих строчных, т. е. так, как написано слово «Корпус» на рис. П.2.4. Высота строчных букв (с) берется на размер меньше, чем прописных, например, если в слове прописная буква выполняется высотой 7 мм, то строчные буквы должны быть высотой 5 мм. На чертежах, выполняемых карандашом, размер шрифта должен быть не менее 3,5 мм.
Кроме указанных выше параметров h, с, d, шрифты характеризуются еще шириной букв (g) и расстоянием между буквами (а).
В заданиях по курсу «Начертательная геометрия и инженерная графика» рекомендуется применять шрифт типа А с наклоном, который представлен на рис. П.2.5.
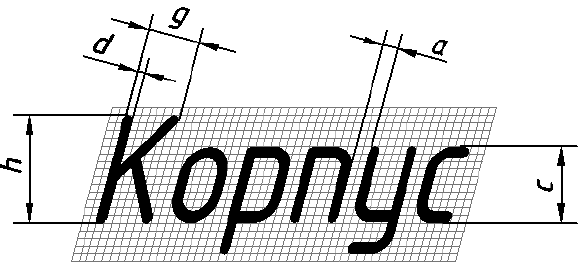
Рис. П.2.5. Начертание букв и цифр русского алфавита шрифта типа А с наклоном
ГОСТ 2.104 — 2006. Основные надписи
ГОСТ 2.104 — 2006 устанавливает формы, размеры и порядок заполнения основных надписей, установленных для применения в технических чертежах.
Для учебных чертежей, выполняемых по проекционному черчению, можно использовать два вида основных надписей:
- стандартную по указанному выше ГОСТу (рис. П.2.6). Ее применение предпочтительно;
- упрощенную учебную (рис. П.2.7). Ее рекомендуется применять по разрешению преподавателя на насыщенном изображениями чертеже по теме «Проекционное» черчение», когда стандартная основная надпись не помещается, (см. рис. П.1.5 и рис. П.1.7).

Рис. П.2.7. Форма и размеры упрощенной основной надписи
ГОСТ 2.306 — 68. Обозначения графические материалов и правила их нанесения на чертежах
Стандарт устанавливает правила штриховки материалов в сечениях. В курсе проекционного черчения, как правило, рассматриваются предметы (детали), которые сделаны из металлов и пластмасс.
Металлы заштриховываются параллельными прямыми тонкими сплошными линиями, проводимыми под углом 45° к горизонту (рис. П.2.8, а). Шаг штриховки (расстояние между линиями штриховки) принимается в пределах от I до 10 мм. В учебных чертежах рекомендуется шаг штриховки 2 . 5 мм в зависимости от площади штриховки. Наклон штриховки может быть влево или вправо.
Пластмассы штрихуются «в клеточку», т. е. перекрестными параллельными прямыми линиями с наклоном 45° (рис. П.2.8, б).
При выполнении любого чертежа необходимо придерживаться следующего правила: на всех изображениях чертежа, выполненных в одном масштабе, один и тот же предмет в сечениях должен быть заштрихован одинаково, т. е. с одинаковым шагом и одним наклоном линий штриховки. Имеются в виду все сечения, как входящие в состав разрезов, так и сечения выносные и наложенные.
Если линии штриховки совпадают по направлению с линиями контура или осевыми линиями, то вместо угла 45° следует брать угол 30° или 60° (см. рис. П.2.8, в). 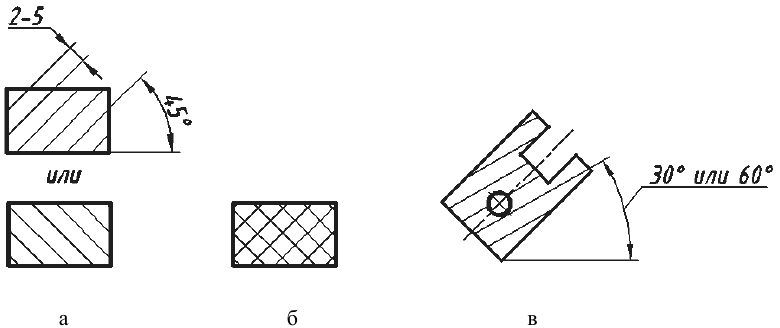
Изображения на технических чертежах
В основе правил построения изображений лежит метод проецирования, подробно рассмотренный в курсе начертательной геометрии. В машиностроении, как правило, применяются параллельные проекции, которые
можно разделить на прямоугольные (ортогональные) и аксонометрические.
Прямоугольные проекции наиболее распространены в машиностроении. В прямоугольных проекциях выполняются все производственные чертежи. Такие чертежи достаточно просты в исполнении, и по ним можно представить себе форму предмета и найти размеры всех его элементов. Однако прямоугольные проекции имеют существенный недостаток – отсутствие наглядности. Для того чтобы по этим проекциям представить истинную форму предмета, необходимо обладать достаточно развитым пространственным мышлением. Этот недостаток ортогональных проекций восполняют аксонометрические проекции, которые более сложны в исполнении, однако обладают наглядностью и выразительностью. Поэтому такие проекции широко применяются для наглядного изображения деталей, узлов, агрегатов машин и конструкций приборов на чертеже, особенно на начальных этапах конструирования. Аксонометрические проекции применяются как самостоятельно, так и в комплексе с ортогональными проекциями.
При выполнении проекционных чертежей полезно помнить, что какую бы сложную форму ни имели реальные изделия (рис. 1), их всегда можно представить как совокупность плоскостей и поверхностей вращения (цилиндрической, конической, сферической, торовой и винтовой). Таким образом, мысленно разбивая деталь на простейшие геометрические объекты и выполняя их проекционные изображения, можно получить прямоугольную или аксонометрическую проекцию изделия целиком.
Прямоугольное проецирование на несколько плоскостей проекций
В общем случае чертеж любого предмета должен содержать графические изображения видимых и невидимых его поверхностей. Согласно ГОСТ 2.305 – 68 ** изображения предметов необходимо выполнять по методу прямоугольного проецирования. При этом предмет предполагается расположенным между наблюдателем и соответствующей плоскостью проекций. Такой метод прямоугольного проецирования называется методом первого угла (или методом Е). За основные плоскости проекций принимают шесть граней куба (рис. 2, а), которые совмещают с плоскостью чертежа, как показано на рис. 2, б.
Изображение на фронтальной плоскости проекций принимают на чертеже в качестве главного. Предмет относительно фронтальной плоскости проекций следует располагать так, чтобы изображение на ней (главное изображение) давало наиболее полное представление о форме и размерах предмета. Изображения на чертеже в зависимости от их содержания согласно стандарту разделяются на виды, разрезы, сечения и выносные элементы.
Видом называется изображение обращенной к наблюдателю видимой части поверхности предмета. Все видимые элементы предмета выполняются сплошными толстыми (основными) линиями. Допускается на видах показывать невидимые части поверхности предмета штриховыми линиями для уменьшения количества изображений в тех случаях, когда невидимые очертания предмета являются несложными. Различают основные, дополнительные и местные виды.
Основными называются виды, получаемые проецированием на основные плоскости проекций. К основным видам (рис. 2, б) относятся:
1 – вид спереди (или главный вид); 2 – вид сверху; 3 – вид слева; 4 – вид справа; 5 – вид снизу; 6 – вид сзади.
Показанное на рис. 2, б расположение видов называется расположением в проекционной связи. Если какой-либо вид расположен с нарушением проекционной связи (смещен относительно главного изображения; отделен от главного изображения другими изображениями; вид расположен не на одном листе с главным изображением), то для него указывают стрелкой направление проецирования, обозначаемое прописной буквой кириллицы, той же буквой обозначают построенный вид (рис. 3).
Дополнительными называют виды, получаемые на плоскостях, не параллельных основным плоскостям проекции. Дополнительные виды применяются в тех случаях, когда какая-либо часть предмета не может быть показана ни на одном из основных видов без искажения формы и размеров и также отмечают стрелкой и надписью (вид А на рис. 4). Допускается поворачивать дополнительный вид, при этом к надписи добавляют знак «повернуто» (вид Б на рис. 4). При необходимости указывают угол поворота после знака «повернуто». Если дополнительный вид расположен в непосредственной проекционной связи с изображением, стрелку и надпись над видом не наносят (рис. 5, 6).
Местным видом называется изображение ограниченной части поверхности предмета. Если местный вид вычерчивают вместе с частью поверхности предмета, на которой находится изображаемый участок, то он ограничивается сплошной волнистой линией (рис. 7).
Если изображаемый элемент вычерчивают только по его контуру, без дополнительного указания части поверхности предмета, лежащей за этим контуром, то волнистую линию не проводят (вид Б на рис. 7).
Местный вид указывают на чертеже так же, как и дополнительный вид. В случаях, когда местные виды располагаются в непосредственной проекционной связи с изображением, допускается их не обозначать. Для удобства чтения чертежа рекомендуется располагать местные виды вблизи исходного изображения.
Кроме рассмотренных выше видов, для изображения искривленных (рис. 8, а) или гнутых предметов (рис. 8, б), которые можно развернуть в одну плоскость без искажения, применяют развертки (или, как их еще называют, развернутые виды). При таком изображении гнутых предметов контуры выполняют сплошной линией, а места изгиба обозначают тонкой штрихпунктирной линией с двумя точками (рис. 8, б). Над изображением развертки помещают знак «развернуто».
На рис. 9 приведены размеры стрелок, указывающих направление взгляда и знаков «повернуто» и «развернуто».
Разрезы
Разрезом называется изображение, полученное мысленным рассечением предмета одной или несколькими плоскостями. На разрезе показывают то, что расположено непосредственно в секущей плоскости и за ней (рис. 10). Допускается изображать не все, что расположено за секущей плоскостью, если этого не требуется для понимания конструкции предмета (рис. 11). Разрез может быть расположен на месте одного из основных видов или на свободном поле чертежа.
При выполнении разреза в определенном месте предмета мысленно проводят секущую плоскость, отбрасывают часть предмета, расположенную между наблюдателем и секущей плоскостью, а затем оставшуюся часть проецируют на соответствующую плоскость проекций. После чего наносятся необходимые обозначения.
Разрез является условным изображением, поскольку проведение секущей плоскости и удаление части предмета, лежащей между наблюдателем и секущей плоскостью, производится мысленно.
Выполняя разрезы, следует помнить, что разрез – это искусственный прием, при котором мысленное рассечение предмета относится только к данному разрезу и не изменяет другие изображения того же предмета. Каждому разрезу соответствует своя собственная секущая плоскость (или плоскости), причем эти плоскости между собой не связаны и один разрез от другого не зависит.
В зависимости от расположения секущих плоскостей относительно плоскостей проекций различают горизонтальные, вертикальные и наклонные разрезы. Горизонтальный разрез (рис. 12) получается при рассечении предмета горизонтальной плоскостью, вертикальный – при рассечении плоскостью,
перпендикулярной горизонтальной плоскости проекций. При этом вертикальный разрез называют фронтальным (рис. 13), если секущая плоскость параллельна фронтальной плоскости проекции, и профильным (рис. 14), если
секущая плоскость параллельна профильной плоскости проекций.
На практике встречаются случаи, когда вертикальный разрез выполняется секущей плоскостью, непараллельной ни фронтальной, ни профильной плоскостям проекций (рис. 15).
Такой разрез строится и располагается в соответствии с направлением взгляда, указанным стрелками на линии, обозначающей след секущей плоскости. Допускается изображать такой вертикальный разрез с поворотом. В этом случае к его обозначению добавляют знак «повернуто». Наклонный разрез (рис. 16) получается при рассечении предмета плоскостью, наклоненной к горизонтальной плоскости проекций. Наклонный разрез допускается изображать с поворотом. В этом случае к его обозначению добавляют знак «повернуто».
В зависимости от направления секущих плоскостей разрезы разделяют на продольные и поперечные. Разрез называется продольным (рис. 17), если секущая плоскость направлена вдоль длины или высоты предмета. Разрез называется поперечным (рис. 18), если секущая плоскость направлена перпендикулярно длине или высоте предмета.
В зависимости от числа секущих плоскостей различают простые и сложные разрезы. Простыми называются разрезы, полученные при мысленном рассечении предмета одной плоскостью. Сложными называются разрезы, полученные при мысленном рассечении предмета двумя или несколькими плоскостями.
Сложный разрез называют ступенчатым, если секущие плоскости параллельны между собой (рис. 19, 20), и ломаным, если секущие плоскости пересекаются под углом, большим 90° (рис. 21, 22).
При повороте секущей плоскости элементы предмета, расположенные за ней, вычерчивают так, как они проецируются на соответствующую плоскость, до которой производится совмещение (рис. 23).
Допускается применение сложных комбинированных разрезов, представляющих собой сочетание ступенчатого и ломаного (рис. 24). При необходимости допускается применять развернутые разрезы (рис. 25). В этом случае в качестве секущей применяют цилиндрическую поверхность, развертываемую затем в плоскость. При выполнении такого разреза над изображениями помещают знак «развернуто».
В зависимости от полноты произведенного разреза они подразделяются на полные и местные. Местные разрезы применяют для выяснения устройства детали лишь в отдельном ограниченном месте (рис. 26). Его ограничивают на виде или волнистой линией (рис. 26, а, б), или линией с изломами (рис. 26, б), и эти линии не должны совпадать с какими-либо другими линиями изображения. Концы ломаной линии должны выступать за контур изображения на 2. 4 мм.
Допускается соединять часть вида и часть соответствующего разреза, разделяя их линией с изломами (рис. 27) или волнистой линией (рис. 29). При этом, как правило, разрезы располагают справа от вертикальной или внизу от горизонтальной оси симметрии. На изображениях симметричных изделий (рис. 28) границей вида и разреза служит ось симметрии (штрихпунктирная линия). В случае если на оси симметрии имеется линия видимого или невидимого контура, то ее видимость нужно сохранить, перенеся линию обрыва левее или правее оси симметрии (рис. 29).
Отметим, что если разрез выполнен на месте главного вида, то его называют главным изображением, а не главным видом.
Обозначение разреза (рис. 30) содержит указание положения секущей плоскости линией сечения (штрихами разомкнутой линии), указание направления проецирования (стрелками на начальном и конечном штрихах) и обозначение секущей плоскости и разреза одной и той же прописной буквой кириллицы, начиная с А, без пропусков и повторений. При сложном разрезе штрихи разомкнутой линии, обозначающие положение секущих плоскостей, проводят также у мест пересечения секущих плоскостей между собой. Начальный и конечный штрихи разомкнутой линии не должны пересекать контур изображения. Буквы наносят около стрелок (при необходимости и в местах перегиба) с внешней стороны угла. Высота буквенных обозначений должна быть на один-два размера шрифта больше размерных чисел чертежа.
Расстояние между изображением детали и штрихом принимается по обстановке, желательно не менее 3 мм. При необходимости начальный и конечный штрихи могут быть расположены внутри контура.
В случаях, подобных показанному на рис. 31, стрелки, указывающие направление взгляда, наносят на одной линии. Не указывают положение секущей плоскости, направление проецирования и не наносят буквенные обозначения, если секущая плоскость совпадает с плоскостью симметрии предмета и параллельна одной из основных плоскостей проекций, а соответствующие изображения расположены на одном и том же листе в непосредственной проекционной связи и не разделены какими-либо другими изображениями (см. рис. 13, 14).
Допускается указывать положение секущей плоскости и направление проецирования без буквенных обозначений для разреза, находящегося в
непосредственной проекционной связи, обеспечивающей однозначное понимание чертежа, как показано на рис. 32. Правила штриховки разрезов рассмотрены в п. 1.6.
Сечения
Сечением называется изображение фигуры, получающейся при мысленном рассечении предмета одной или несколькими плоскостями. При необходимости можно применять в качестве секущей цилиндрическую поверхность, развертываемую затем в плоскость. В отличие от разреза, в сечении показывают только то, что получается непосредственно в секущей плоскости. На рис. 33 для сравнения показаны разрез А – А и сечение Б – Б.
Сечения, не входящие в состав разреза, по месту своего расположения разделяют на вынесенные и наложенные. Вынесенным называется сечение, расположенное вне контура основного изображения (рис. 34, а). Наложенным называется сечение, расположенное на проекции предмета (рис. 34, б). Применение вынесенных сечений предпочтительно.
Наложенные сечения вычерчивают сплошными тонкими линиями непосредственно на самом виде, причем контур изображения в месте расположения наложенного сечения не прерывают (рис. 35). Вынесенные сечения располагают на свободном поле чертежа и ограничивают сплошными основными линиями (рис. 36). Допускается изображать вынесенное сечение в разрыве изображения (рис. 37).
В зависимости от расположения секущей плоскости относительно оси детали сечения подразделяются на нормальные и наклонные. Нормальным называется сечение в том случае, если секущая плоскость перпендикулярна оси предмета (рис. 38), наклонным – если секущая плоскость наклонена к оси предмета (рис. 39).
В зависимости от количества секущих плоскостей различают простые и сложные сечения. Простые сечения получаются при рассечении предмета одной секущей плоскостью, сложные – при рассечении предмета двумя или несколькими плоскостями. Наиболее часто применяют простые сечения. Сложные сечения допускается применять тогда, когда рассекаемые элементы предмета не параллельны друг другу. В общем случае положение секущей плоскости и надпись над сечением на чертежах указывают так же, как и для разрезов (рис. 38, 39).
Если вынесенное сечение имеет симметричную форму и расположено вблизи изображения на продолжении следа секущей плоскости, то след секущей плоскости обозначается тонкой штрихпунктирной линией, буквами не обозначается, направление взгляда не указывается и сечение не подписывается. Для симметричных наложенных сечений и сечений, расположенных в разрыве изображения, след секущей плоскости не указывается и сечение не подписывается (рис. 40).
При этом секущую плоскость следует располагать таким образом, чтобы на изображении получалось нормальное поперечное сечение.
Для несимметричных сечений, расположенных в разрыве или наложенных, линию сечения проводят со стрелками, но буквами не обозначают (рис. 41).
Сечения по построению и расположению должны соответствовать направлению, указанному стрелками. Допускается располагать сечение повернутым. В этом случае его изображение сопровождают знаком «повернуто» (рис. 42, а). Знак «повернуто» не ставят, если секущие плоскости расположены под разными углами (рис. 42, б).
Если на чертеже имеется несколько одинаковых сечений, относящихся к одному и тому же изделию, то линию сечения обозначают одной буквой и вычерчивают одно сечение (рис. 43). Если расположение одинаковых сечений точно определено размерами или изображением, то допускается наносить одну линию сечения и вычерчивать одно сечение (рис. 44). Допускается указывать количество сечений в надписи сечения (рис. 45).
Если секущая плоскость проходит через ось поверхности вращения, ограничивающей отверстие или углубление, то контур отверстия или углубления в сечении показывают полностью (рис. 46).
Если сечение получается состоящим из отдельных частей, то необходимо применить разрез (рис. 47). Правила штриховки сечений рассмотрены в п. 1.6.
Выносные элементы
При изображении детали на чертеже в мелком масштабе конструкция отдельных ее частей может быть неясна. Поэтому возникает необходимость в применении выносных элементов, которые позволяют исключить необходимость увеличения масштаба всего изображения для конкретизации отдельных конструктивных особенностей изделия.
Выносным элементом называется дополнительное отдельное изображение (обычно увеличенное) какой-либо части предмета, требующей графического или иного пояснения в отношении формы, размеров и других данных ввиду мелкого ее изображения.
Выносной элемент может содержать подробности, не указанные на соответствующем изображении, и может отличаться от него по содержанию (например, изображение может быть видом, а выносной элемент – разрезом).
При применении выносного элемента соответствующее место отмечают на виде, разрезе или сечении замкнутой сплошной тонкой линией (окружностью или овалом) с обозначением прописной буквой кириллицы на полке линии-выноски. Над выносным элементом указывается та же буква и масштаб, в котором выполнен выносной элемент (рис. 48).
Выносной элемент следует располагать как можно ближе к соответствующему месту на изображении предмета.
Графическое обозначение материалов в разрезах и сечениях
Для изготовления изделий в технике применяется большое число различных материалов. Материал, из которого должно быть изготовлено изделие, указывают соответствующим обозначением в основной надписи чертежа. Однако для удобства пользования чертежом в сечениях (в том числе и входящих в состав разрезов) наносят установленные ГОСТ 2.306 – 68* графические обозначения материалов, которые характеризуют их лишь в общих чертах. Некоторые из этих обозначений приведены в таблице, на с. 31.
Штриховка выполняется тонкими сплошными линиями. Параллельные линии штриховок проводят под углом 45° к линии рамки чертежа (рис. 49, а) или к оси вынесенного или наложенного сечения (рис. 49, б).
Расстояние между линиями выбирается в зависимости от площади сечения (чем больше площадь сечения, тем относительно реже штриховка) и необходимости разнообразить штриховку смежных сечений. Для учебных чертежей рекомендуется принимать расстояние между линиями штриховки, равным 2. 3 мм. Расстояние между параллельными линиями штриховки должно быть одинаковым для всех выполненных в одном масштабе изображений данной детали на чертеже. Линии штриховки могут наноситься с наклоном влево или вправо, но в одну и ту же сторону на всех сечениях, относящихся к одной и той же детали, независимо от количества листов, на которых расположены чертежи этих сечений. При совпадении направления линий штриховки с контурными или осевыми линиями вместо угла наклона 45° применяют угол 30 или 60° (рис. 50).
Штриховку смежных сечений наносят для одного сечения вправо, для другого – влево или изменяют расстояние между линиями (рис. 51, а), кроме того, применяют сдвиги линий штриховки (рис. 51, б). При штриховке «в клетку» расстояние между линиями штриховки в каждом сечении должно быть разным (рис. 52).
Большие площади, а также при указании профиля грунта рекомендуется штриховать только у контурных линий узкой полоской равномерной толщины (рис. 53).
Узкие площади сечений, шириной на чертеже менее 2 мм, допускается зачернять (рис. 54), оставляя просвет между смежными сечениями 0,8…1,0 мм. Узкие и длинные площади сечений рекомендуется штриховать участками (рис. 55).
Графические обозначения материалов:
Примечания:
- Композиционные материалы, содержащие металлы и неметаллические материалы, обозначают как металлы.
- Графическое обозначение древесины применяется в тех случаях, когда нет
- необходимости указывать направление волокон.
- Графическое обозначение керамики и силикатных материалов следует применять для обозначения кирпичных изделий (обожженных и необожженных), огнеупоров, строительной керамики, электротехнического фарфора, шлакобетонных блоков и т.п.
- Допускается применять дополнительные обозначения материалов, не предусмотренных в стандарте, поясняя их на чертеже.
Соприкасающиеся сечения одной и той же детали штрихуют в одну сторону без изменения шага штриховки (рис. 56). Графические обозначения, отличные от прямых линий штриховки, выполняют от руки.
Условности и упрощения, применяемые при выполнении изображений
В целях уменьшения трудоемкости и ускорения процесса разработки чертежей, уменьшения расхода бумаги на их оформление, повышения выразительности чертежей ГОСТ 2.305 – 68 ** устанавливает следующие условности и упрощения.
Если вид, разрез или сечение представляют собой симметричную фигуру, допускается вычерчивать половину изображения или немного более половины изображения с проведением в последнем случае волнистой линии (рис. 57).
Если предмет имеет несколько одинаковых, равномерно расположенных элементов (отверстий, зубьев, пазов, спиц и т. д.), то на его изображении полностью показывают один – два таких элемента, а остальные упрощенно или условно (рис. 58, а и рис. 59), с указанием их количества. Допускается также изображать лишь часть такого предмета (рис. 58, б) с надлежащими указаниями о количестве элементов, их расположении и т.д.
Плавный переход одной поверхности в другую показывают условно тонкой линией или совсем не показывают (рис. 60). Допускается упрощенно изображать линии пересечения поверхностей, если по условиям производства не требуется их точного построения. Например, вместо лекальных кривых можно проводить дуги окружности и прямые (рис. 61).
Такие элементы деталей, как спицы маховиков, шкивов, зубчатых колес, тонкие стенки типа ребер жесткости и т. п., показывают рассеченными, но для большей наглядности не заштрихованными, если секущая плоскость направлена вдоль их оси или длинной стороны элемента (рис. 58, 63). Если в подобных элементах детали имеется отверстие или углубление, то применяют местный разрез (рис. 24, 64).
При изображении деталей, имеющих постоянные или закономерно изменяющиеся поперечные сечения (стержни, валы, трубопроводы, цепи, фасонный прокат, шатуны, опоры и т.п.), для экономии места допускается
изображать их с разрывами (рис. 65). Место обрыва ограничивается сплошной волнистой линией, которая проводится от руки, или, для участков большой протяженности, сплошной линией с изломами. Плоские участки поверхности детали рекомендуется выделять диагоналями, проводимыми сплошными тонкими линиями (рис. 66).
На чертежах изделий с накаткой, сплошной сеткой, орнаментом, рифлением и т.д. эти элементы допускается изображать частично с возможным упрощением (рис. 67).
Для показа конструкции отверстий в ступицах шкивов, зубчатых и червячных колес и т.п. деталей, а также шпоночных пазов на валах допускается вместо второго изображения детали давать лишь контур отверстия (рис. 68, а) или паза (рис. 68, б).
Пластины, а также элементы деталей (отверстия, фаски, пазы, углубления и т.п.) размером на чертеже 2 мм и менее рекомендуется изображать с отступлением от масштаба, принятого для всего изображения, в сторону увеличения. Незначительный уклон допускается показывать с увеличением.
Незначительную конусность также допускается изображать с увеличением или проводить только одну линию, соответствующую меньшему диаметру конуса (рис. 69). При выполнении разрезов допускается показывать элементы детали,
расположенные перед секущей плоскостью (рис. 70). Такое изображение называется наложенной проекцией. Наложенная проекция выполняется
штрихпунктирной утолщенной линией.
Допускается изображать в разрезе отверстия, расположенные на круглом фланце, не попадающие в секущую плоскость (рис. 71).
Применение условностей и упрощений при построении изображений сокращает время, затрачиваемое на разработку графической документации, и ведет к сокращению сроков проектирования, повышению его качества. Однако следует иметь ввиду, что применение упрощений не должно приводить к снижению ясности чертежа.
Наглядные аксонометрические изображения
Сущность метода параллельного аксонометрического проецирования состоит в том, что предмет относят к некоторой прямоугольной системе координат и затем проецируют его параллельными лучами на произвольно выбранную плоскость аксонометрических проекций вместе с этой системой.
Сущность метода аксонометрического проецирования
Плоскость аксонометрических проекций называют также картинной плоскостью. На рис. 72 показана точка А, отнесенная к системе прямоугольных координат Oxyz. Проведем через нее проецирующий луч, параллельный вектору 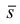
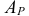
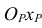
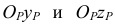
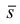
Аксонометрические проекции различаются по углу φ, который составляет вектор направления проецирования 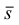
Известно, что положение любой точки в пространстве определяют три ее координаты – x, y и z. На рис. 73 показано построение аксонометрической проекции точки А, положение которой определяют координаты 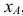
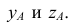
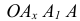
Коэффициентом (или показателем) искажения называется отношение длины проекции отрезка оси на картинной плоскости к его истинной длине.
Коэффициенты искажения по направлениям каждой из координатных осей или по направлениям, им параллельным, определяются по формулам:
Можно показать, что между коэффициентами искажения и углом φ существует следующая зависимость:
Для прямоугольной аксонометрии, когда φ = 90º, это соотношение принимает вид
В зависимости от соотношения коэффициентов искажения, различают изометрические, диметрические и триметрические аксонометрические проекции. Изометрической проекцией (или изометрией) называется такая
аксонометрическая проекция, у которой все коэффициенты искажения равны между собой (k = m = n). Если равны между собой лишь два коэффициента искажения (k = m ≠ n), то аксонометрическая проекция называется диметрической (или диметрией). Если же все три коэффициента искажения не равны между собой (k ≠ m ≠ n ≠ k), то аксонометрия называется триметрической (или триметрией). Понятно, что изометрические, диметрические и триметрические проекции могут быть как прямоугольными, так и косоугольными.
Обратимость аксонометрической проекции, т.е. возможность определения натуральных размеров изображенного объекта, обеспечивается путем указания на нем показателей искажения (или наличием условий для их определения) и возможности построения аксонометрической координатной ломаной любой точки поверхности, принадлежащей изображенному объекту. Построение аксонометрии при помощи координатных ломаных производят достаточно редко. Ими пользуются в тех случаях, когда нельзя применить какой-либо частный прием, например, для построения линий перехода и других кривых линий.
На практике аксонометрическую проекцию предмета строят, проводя отрезки
прямых соответствующей длинны (с учетом показателей искажения) параллельно аксонометрическим осям. На аксонометрической проекции могут быть нанесены размеры, обеспечивающие его обратимость. В этом случае нет необходимости в указании показателей искажения по осям.
Разрезы на аксонометрических проекциях выполняют, как правило, путем сечения объекта плоскостями, параллельными координатным. При этом линия, ограничивающая разрез, вычерчивается как линия видимого контура. Применяемые в отечественной конструкторской документации аксонометрические проекции стандартизованы по ГОСТ 2.317 – 69. К стандартным аксонометрическим проекциям относятся: прямоугольная изометрия, прямоугольная диметрия, косоугольные фронтальная и горизонтальная изометрии и косоугольная фронтальная диметрия.
Прямоугольная изометрия
В прямоугольной изометрии аксонометрические оси расположены под углами 120º друг к другу. При этом ось Оz располагают вертикально, а оси Оx и Оy под углами 30º к горизонтальному направлению (рис. 74, а).
Рассмотрим различные способы построения изометрических осей. Выполняя построение осей первым способом (рис. 74, б), на горизонтальной прямой, проходящей через центр аксонометрической системы координат, откладываем в обе стороны от точки О семь равных отрезков произвольной длины. Из крайних точек этих отрезков вниз по вертикали откладываем слева и справа по четыре таких же отрезка. Построенные точки соединяем с точкой О и получаем направления аксонометрических осей Ох и Оу.
Построение осей вторым способом (рис. 74, в) выполняется в следующей последовательности. Строим окружность произвольного радиуса R с центром в точке О. Затем из точки пересечения полученной окружности с вертикальной осью, проходящей через точку О, как из центра, проводим дуги окружностей такого же радиуса до пересечения с исходной окружностью. Построенные точки соединяем с точкой О и получаем направления аксонометрических осей Ох и Оу.
Третий способ (рис. 74, г) предполагает использование угольника с углами 30º, 60º и 90º. Порядок построения понятен из рисунка. Для построения изображения предмета в изометрии необходимо все его линейные размеры, параллельные осям, умножить на коэффициент искажения 0,82, а затем уже откладывать их на аксонометрическом чертеже. Полученное изображение называют нормальным или точным (рис. 75, а). Стандарт предусматривает построение и упрощенной изометрической проекции без сокращения размеров по осям координат. При этом получается увеличенное в 1,22 раза по отношению к оригиналу изображение
предмета без нарушения пропорций между отдельными элементами. Такое
изометрическое изображение называется увеличенным (рис. 75, б), а коэффициенты искажения становятся приведенными. На практике, как правило, применяется изометрическая проекция, дающая увеличенное изображение.
Изометрическими проекциями окружностей, расположенных в плоскостях проекций или плоскостях, параллельных им, являются эллипсы (рис. 76). Соотношения больших и малых осей эллипсов во всех плоскостях проекций одинаковы и равны: большие оси – 1,22d, малые – 0,71d, где d – диаметр изображаемой окружности.
Расположение осей эллипсов зависит от положения проецируемой окружности. В общем случае для всех видов прямоугольных аксонометрических проекций справедливо правило: большая ось эллипса всегда перпендикулярна к отсутствующей в плоскости данной окружности оси, а малая ось эллипса – направлена вдоль этой оси. Например, большая ось эллипса, в который проецируется окружность, лежащая во фронтальной плоскости проекций, расположена перпендикулярно оси Оy, а малая – направлена по этой оси, поскольку именно ось Оy отсутствует во фронтальной плоскости проекций (рис. 76).
Величина осей эллипса может быть вычислена по указанным соотношениям или определена графически. Графическое определение величин большой и малой осей эллипса в изометрии, в зависимости от диаметра d проецируемой окружности, показано на рис. 77. Как правило, на практике для упрощения построений эллипсы в изометрии заменяют четырехцентровыми овалами. Рассмотрим два способа построения таких овалов.
Для построения овала первым способом (рис. 78) проводим изометрические оси Ох и Оу и откладываем на них в обе стороны от точки О отрезки, равные радиусу заданной окружности (рис. 78, б). Через полученные точки 1, 2, 3, 4 проводим прямые, параллельные аксонометрическим осям, и получаем ромб ABCD, который представляет собой изометрию квадрата, описанного вокруг окружности (рис. 78, а). Вершины А и С полученного ромба, лежащие на короткой диагонали, являются центрами больших дуг овала.
Соединяем лучами точку А с точками 2 и 3 и на пересечении этих лучей с большой диагональю BD ромба получаем центры малых дуг овала – 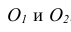
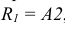
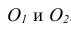
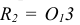
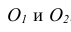
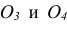
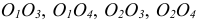
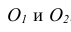
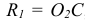
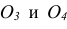
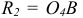
На рис. 80 показан пример построения наглядного изображения детали в прямоугольной изометрической проекции.
Прямоугольная диметрия
Стандарт регламентирует применение прямоугольной диметрической проекции, у которой ось Оz расположена вертикально, ось Ох наклонена под углом 7°10′, а ось Оу – под углом 41°25′ к линии горизонта (рис. 81). При построении прямоугольной диметрии сокращение длин по оси Оу принимают вдвое больше, чем по двум другим, т.е. полагают, что 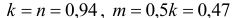
Построение аксонометрических осей диметрии можно проводить двумя способами (рис. 82). Выполняя построение осей первым способом (рис. 82, а), на горизонтальной прямой, проходящей через точку О, откладываем в обе стороны от точки О восемь равных отрезков произвольной длины. Из крайних точек этих отрезков вниз по вертикали откладываем слева один такой же отрезок, а справа – семь. Построенные точки соединяем с точкой О и получаем направления аксонометрических осей Ох и Оу. Построение осей вторым способом (рис. 82, б) выполняется в следующей последовательности. На вертикальной прямой вниз от точки О откладываем отрезок OD произвольной длины, а вверх – отрезок OA = 2ОD.
Затем из точки О, как из центра, проводим дугу окружности радиусом 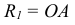
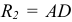
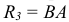
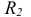
Диметрическими проекциями окружностей, расположенных в плоскостях проекций или плоскостях, параллельных им, так же как и в изометрии являются эллипсы, большие и малые оси которых расположены согласно правилу, сформулированному в п. 2.2 (рис. 83, а). Длина большой оси для всех эллипсов одинакова и равна 1,06d (где d – диаметр изображаемой окружности), длина малой оси различна: для фронтальной плоскости проекций и плоскостей, параллельных ей, она составляет 0,95d, для горизонтальной и профильной плоскостей проекций и плоскостей, параллельных им, – 0,35d.
При построении прямоугольной диметрической проекции эллипсы заменяют четырехцентровыми овалами. Построение четырехцентровых овалов для горизонтальной и профильной плоскостей проекций и плоскостей, параллельных им, производится в следующей последовательности (рис. 83, б). Через центр системы координат О проводят две взаимно перпендикулярные прямые и откладывают на горизонтальной оси от точки О влево и вправо половину большой оси эллипса (АО = ОВ =1,06d/2), а на вертикальной оси – вверх и вниз половину малой оси (СО = ОD =0,35d/2). Затем на вертикальной прямой от
точки О вверх и вниз откладывают отрезки 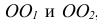
большой оси эллипса (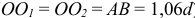
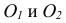
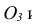
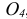
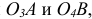
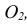
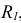
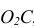
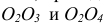
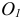
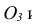
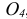
Построение овала, заменяющего эллипс во фронтальной плоскости проекций, показано на рис. 83, в. Проводят оси диметрии Ox, Оy, Оz и из точки О восставляют перпендикуляр к оси Оу (малая ось эллипса совпадает с направлением оси Оу, а большая – перпендикулярна к ней). На осях Ох и Оz откладывают величину радиуса заданной окружности, т. е. OМ = ON= OК = OL= d/2, и получают точки М, N, K, L, которые являются точками сопряжения дуг овала. Из точек М и N проводят горизонтальные прямые, которые в пересечении с осью Оу и перпендикуляром к ней дают точки 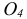
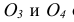
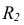
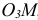
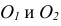
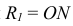
На рис. 84 показан пример построения наглядного изображения детали в прямоугольной диметрической проекции.
Косоугольные изометрии
Стандарт предусматривает применение двух видов косоугольной изометрической проекции: фронтальной и горизонтальной. Направление аксонометрических осей фронтальной косоугольной изометрической проекции показано на рис. 85, а. Угол наклона оси Оy к горизонтальной линии должен составлять 45º. Допускается применять фронтальную изометрию с углами наклона оси Оy в 30º или 60º. Все три показателя искажения по осям Оx, Оy и Оz равны единице.
Окружности, находящиеся в плоскостях, параллельных фронтальной плоскости проекций, изображаются в косоугольной фронтальной изометрии в натуральную величину, а окружности, лежащие в плоскостях, параллельных горизонтальной и профильной плоскостям, проецируются в эллипсы (рис. 85, б). Большая ось эллипса в горизонтальной плоскости составляет угол 22º30′ с осью Ox, а в профильной плоскости – такой же угол с осью Oz. Большие оси этих эллипсов равны 1,3d, а малые – 0,54d, где d – диаметр изображаемой окружности. Эллипсы заменяются овалами, которые вычерчиваются по двум известным осям следующим образом (рис. 86). На прямой, соединяющей точки А и С,откладывают от точки С отрезок СМ, равный разности полуосей овала, т. е. СМ = ОK – ОС. Из середины отрезка AM восставляют перпендикуляр и продолжают его до пересечения с осями овала в точках 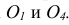
Затем определяют симметричные им точки 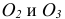
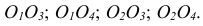
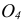
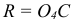
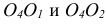
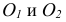
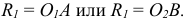
Направление аксонометрических осей горизонтальной косоугольной изометрической проекции показано на рис. 88, а. Угол наклона оси Оy к горизонтальной линии должен составлять 30º.Допускается применять горизонтальную аксонометрию с углами наклона оси Оy к горизонтальному
направлению в 45º и 60º, сохраняя угол 90º между осями Оx и Оy. Коэффициенты искажения по всем трем осям одинаковы и равны единице.
Окружности, находящиеся в плоскостях, параллельных горизонтальной плоскости проекций, изображаются в аксонометрии без искажения, а окружности, лежащие в плоскостях, параллельных фронтальной и профильной плоскости, проецируются эллипсами (рис. 88, б). Большая ось эллипса, который является проекцией окружности, расположенной во фронтальной плоскости, наклонена к оси Oz под углом 15º, величина большой оси этого эллипса равна 1,37d, а малой – 0,37d. Эллипс строится как овал по двум заданным осям (см. рис. 86). Большая ось эллипса, который является проекцией окружности, расположенной в профильной плоскости, наклонена к оси Oz под углом 30º, величина большой оси равна 1,22d, а малой – 0,71d. Сопряженные диаметры эллипсов, то есть диаметры, параллельные аксонометрическим осям, во всех случаях равны d. Построение эллипса выполняют по правилам построения проекций окружностей в прямоугольной изометрии.
На рис. 89 показан пример построения наглядного изображения детали в горизонтальной косоугольной изометрической проекции.
Косоугольная фронтальная диметрия
В косоугольной фронтальной диметрии ось Oz расположена вертикально, ось Ox – горизонтально, а ось Oy наклонена к горизонтальной оси под углом 45° (рис. 90, а). Допускается применение косоугольной фронтальной диметрии с углами наклона оси Oy, равными 30° или 60°. Коэффициенты искажения по осям Ox и Oz равны k = n = 1, а по оси Oy коэффициент m = 0,5. Следовательно, все плоские фигуры, размещенные параллельно фронтальной плоскости проекций, изображаются во фронтальной диметрии без искажения размеров и углов.
В косоугольной диметрии окружность, лежащая во фронтальной плоскости, изображается без искажения (рис. 90, б). Это обстоятельство представляет существенное преимущество при вычерчивании фронтальной диметрии деталей цилиндрической формы или с большим числом цилиндрических отверстий. Окружности, принадлежащие горизонтальной и профильной плоскостям, изображаются в виде эллипсов такой же формы и размеров, как и в
прямоугольной диметрии, то есть большая ось этих эллипсов равна 1,06d, а малая – 0,35d. В отличие от прямоугольной диметрии, большая ось эллипса в горизонтальной плоскости наклонена к оси Ox под углом 7º14′, а в профильной плоскости – под тем же углом к оси Oz (рис. 90, б). Упрощенное построение эллипсов в виде овалов выполняют по тем же правилам, что и в прямоугольной диметрии.
На рис. 91 показан пример построения наглядного изображения детали во фронтальной косоугольной диметрической проекции.
Условности и нанесение размеров в аксонометрии
При нанесении размеров на чертежах, выполненных в аксонометрических проекциях, выносные линии проводятся параллельно аксонометрическим осям, а размерные линии – параллельно измеряемому отрезку (рис. 92). В отличие от проекционных чертежей, в аксонометрии при рассечении поверхности предмета заштриховывают ребра жесткости, спицы маховиков, колес и другие подобные элементы (рис. 93), попавшие в секущую плоскость. Места плавных переходов изображают тонкими линиями.
Линии штриховки рассеченных поверхностей в аксонометрических проекциях выполняют параллельно одной из диагоналей квадратов, стороны которых расположены в соответствующих координатных плоскостях параллельно аксонометрическим осям. Направление штриховки рекомендуется выбирать в соответствии со схемами, показанными на рис. 94. Резьбу в аксонометрических проекциях изображают условно по ГОСТ 2.311 – 68. В случае необходимости, допускается частично изображать профиль резьбы (рис. 93).
Проекционное черчение
Проекционное черчение рассматривает построение изображений пространственных предметов на плоскости и имеет важное значение при изучении курса инженерной графики.
Изображение предметов на чертеже
На чертежах изображения предметов выполняются по способу прямоугольного проецирования, изложенном в курсе начертательной геометрии, с применением условностей, установленных правилами ГОСТ 2.305-2008 и других Государственных стандартов ЕСКД.
Прямоугольные проекции, построенные с применением указанных условностей, в ГОСТе называют изображениями. Для аксонометрических проекций, помимо прямоугольного, может применяться косоугольное проецирование.
В отличие от начертательной геометрии, где изображаются оси проекций, при выполнении чертежей применяется безосная система (без указания осей проекций и линий проекционной связи).
На чертежах в качестве баз для построения и определения формы и размеров изображения используются контуры, оси и центры симметрии проецируемого предмета. Вычерчивание изображения следует начать с проведения осей, нахождения центров симметрии и проведения линий видимого контура, от которых откладывают размеры и ведут построения.
При разработке технических чертежей деталей машин и других геометрических объектов (рис. 3,1) изображения должны выполняться по методу прямоугольного проецирования. При этом предполагается, что предмет расположен между наблюдателем и соответствующей плоскостью (рис. 3.2).
За основные плоскости проекций принимают шесть граней куба, которые разворачивают и совмещают с плоскостью так, как показано на рис. 3.2, причем грань 6 допускается размещать рядом с гранью 4. Изображения на фронтальной плоскости проекций называется главным. Относительно этой плоскости проекций предмет следует располагать так, чтобы изображение на ней давало наиболее полное представление о форме и размерах предмета.
Вес изображения на чертеже в зависимости от их содержания разделяются на виды, разрезы и сечения.
Видом называется изображение обращенной к наблюдателю видимой части поверхности предмета. Расположение видов на чертеже показано на рис. 3.3.
Разрезом называется изображение предмета, мысленно рассеченного одной или несколькими плоскостями, при этом мысленное рассечение предмета относится только к данному разрезу и не влечет за собой изменения других изображений того же предмета. Па разрез показывается то, что получается на секущей плоскости и что расположено за ней. Допускается изображать не все, что расположено за секущей плоскостью, если этого нс требуется для понимания конструкции предмета. На чертеже предмет в разрезе заштриховывают.
Сечением называется изображение, получающееся при мысленном рассечении предмета одной или несколькими плоскостями. Па сечении показывается только то, что находится непосредственно в секущей плоскости.
Разрезы и сечения выявляют внутренние очертания изображаемого предмета.
Количество изображений (видов, разрезов, сечений) на чертеже должно быть наименьшим, но достаточным для полного понимания формы и размеров предмета. Это значит, что в каждом отдельном случае от исполнителя чертежа требуется, грамотно используя условные обозначения, знаки и надписи, согласно требованиям государственных стандартов, выбирать и располагать виды, разрезы и сечения так, чтобы свести к минимуму графические построения.
Виды
Виды, получаемые при проецировании предмета на шесть основных плоскостей проекций (граней куба), называются основными видами.
Наименование основных видов следующее:
- 1 — вид спереди (главный вид);
- 2 — вид сверху;
- 3 — вид слева;
- 4 — вид справа;
- 5 — вид снизу;
- 6 — вид сзади.
Основные виды располагаются в определенном порядке, как показано на рис. 3.3.
На чертеже виды располагают по отношению к главному виду (рис. 3.3) в такой последовательности: вид сверху — под главным видом, вид слева — справа от главного вида, вид снизу — над главным видом, а вид справа — слева от главного вида. Вид сзади разрешается помещать справа от вида слева или с левой стороны от вида справа.
Названия видов на чертежах не надписывают, за исключением случая, когда виды сверху, справа, слева, снизу, сзади не находятся в непосредственной проекционной связи с главным изображением (видом или разрезом, изображенным на фронтальной плоскости проекций). Тогда направление проектирования должно быть указано стрелкой около соответствующего изображения. Над стрелкой и над полученным изображением (видом) следует нанести одну и ту же прописную букву русского алфавита (рис. 3.4). Буквенные обозначения присваиваются в алфавитном порядке без повторений и без пропусков. Буквы И, О, X, Ъ,
Ы, Ь ,Ё, 3, Ч, согласно ГОСТу 2.316-2008, при выполнении чертежей не наносят.
Когда какая-либо часть предмета не может быть показана на одном из основных видов без искажения ее формы и размеров или можно ограничиться не целым видом, а изображением узко ограниченного места на поверхности предмета, применяют дополнительные и местные виды.
Дополнительными называются виды, получаемые на плоскостях, не параллельных ни одной из основных плоскостей проекций (рис. 3.5). Дополнительный вид на чертеже должен быть отмечен прописной буквой (рис. 3.5, о, б, г), а у изображения предмета, связанного с дополни-тельным видом должна быть поставлена стрелка, указывающая направление взгляда, где дополнительный вид обозначают той же буквой.
Когда дополнительный вид расположен в непосредственной связи с соответствующим изображением, стрелку и обозначение вида не наносят (рис. 3.5, а).
Дополнительный вид допускается повертывать (рис. 3.5, в, г), при этом буквенное обозначение вида должно быть дополнено знаком 
Местным видом называется изображение отдельного узко ограниченного места поверхности предмета.
Местный вид обозначается на чертеже подобно дополнительному виду и применяется в тех случаях, когда из всего вида только часть его необходима для уточнения формы предмета, остальная же часть вида не дает дополнительных сведений о предмете (рис. 3.6):
- — если изображение имеет ось симметрии, то допускается показывать его половину (рис. 3.6 — вид «А»);
- — если местный вид выполняется в проекционной связи по направлению взгляда, то стрелку и надпись над местным видом не наносят;
- — местный вид может быть ограничен линией обрыва;
- — местный вид может и не быть ограничен линией обрыва -вид «Б».
Разрезы
В зависимости от положения секущей плоскости относительно горизонтальной плоскости проекций разрезы бывают:
горизонтальные — секущая плоскость параллельна горизонтальной плоскости проекций (рис. 3.11, разрез А-А);
вертикальные — секущая плоскость перпендикулярна горизонтальной плоскости проекций (например, рис. 3.8, разрезы А-А, Б-Б);
наклонные — секущая плоскость составляет с горизонтальной плоскостью проекций угол, отличный от прямого.
Вертикальный разрез называется фронтальным, если секущая плоскость параллельна фронтальной плоскости проекций (рис. 3.8, разрез А-А) и профильным, если секущая плоскость параллельна профильной плоскости проекции (рис. 3.8, разрез Б-Б).
В зависимости от числа секущих плоскостей разрезы бывают: простыми — при одной секущей плоскости (рис. 3.8, 3.9, 3.11); сложными — при двух и более секущих плоскостях.
Сложные разрезы в свою очередь подразделяют на ступенчатые, если секущие плоскости параллельны (рис. 3.12), и ломаные, если секущие плоскости пересекаются (рис. 3.13).
Форму предмета в отдельном узко ограниченном его месте определяет местный разрез (рис. 3.14, 3.15).
Положение (след) секущей плоскости показывают на чертеже разомкнутой линией (рис. 3.7, а), называемой линией сечения. При простом разрезе показывают только начальный и конечный штрихи линий сечения (рис. 3.8), а при сложном показывают се штрихи и в местах перегибов (рис. 3.12, 3.13). На начальном и конечном штрихах линии сечения ставят стрелки (рис. 3.7, а), указывающие направление взгляда (проецирования). Начальный и конечный штрихи этой линии не должны пересекать контур изображения.
У начала и конца линии сечения ставят одну и ту же прописную букву русского алфавита (рис. 3.7, б), разрез отмечается надписью по типу «А-А» (всегда только двумя буквами через тире).
В том случае, когда секущая плоскость совпадает с плоскостью симметрии детали и разрез расположен на одном листе в проекционной связи с другими изображениями детали, не обозначается положение секущей плоскости и разрез надписью не сопровождается.
На разрезе невидимые линии внутреннего контура становятся видимыми и изображаются сплошными основными линиями.
Мысленное рассечение предмета относится только к данному разрезу и не влечет за собой изменения других изображений того же предмета.
Штриховка на всех изображениях детали выполняется в одном направлении, с правым или левым наклоном, под углом 45° к горизонтальной линии чертежа тонкими линиями, условно приняв, что все детали, приведенные в примерах, металлические. Расстояние между штриховыми линиями должно быть одинаковым.
Простые разрезы
Простым разрезом называется разрез, получаемый при рассечении детали одной секущей плоскостью. Чаще всего применяются вертикальные и горизонтальные разрезы.
Вертикальными называются разрезы, образованные секущими плоскостями, параллельными фронтальной или профильной плоскостям проекций.
Вертикальный разрез называется фронтальным, если секущая плоскость параллельна фронтальной плоскости проекций, и профильным, если секущая плоскость параллельна профильной плоскости проекций.
Горизонтальными разрезами называются разрезы, образованные секущими плоскостями, параллельными горизонтальной плоскости проекций.
Горизонтальные, фронтальные и профильные разрезы могут размещаться на месте соответствующих основных видов.
На рис. 3.7 выполнены два вертикальных разреза: фронтальный (А-А) и профильный (Б-Б), где деталь не имеет осей симметрии, поэтому на чертеже указано положение секущих плоскостей и соответствующие им разрезы сопровождаются надписями.
Для упрощения построения чертежа на одном изображении допускается соединять часть вида и часть разреза.
При соединении симметричных частей вида и разреза, если с осью симметрии совпадает проекция какой-либо линии, например ребра (рис. 3.9), то вид от разреза отделяется тонкой сплошной волнистой линией, проводимой правее (рис. 3.9, а) или левее (рис. 3.9, 6) оси симметрии.
Если деталь симметрична (рис. 3.10), то можно соединить половину вида и половину разреза (рис. 3.11), разделяя их штрихпунктирной тонкой линией, являющейся осью симметрии. Часть разреза может располагаться правее (рис. 3.12, а, разрез А-А,) или ниже (рис. 3.12, б, разрез А-А) оси симметрии, разделяющей часть вида с частью разреза, причем разрез А-А на рис, 3.12, а предпочтительнее.
Сложные разрезы
Сложными называются разрезы, получаемые с помощью двух и более секущих плоскостей. Они применяются в случаях, когда количество элементов деталей, их форма и расположение не могут быть изображены на простом разрезе одной секущей плоскостью и это вызывает необходимость применения нескольких секущих плоскостей.
Сложные разрезы разделяются на ступенчатые и ломаные. Они могут быть так же, как и простые разрезы, горизонтальными, фронтальными и профильными. Сложные разрезы бывают и комбинированными, т. е. состоящими из ступенчатых и ломаных разрезов.
Ступенчатыми разрезами называются разрезы, выполненные нескольким и параллельным и секущими плоскостями.
Разрез на рис. 3.12 осуществлен тремя секущими фронтальными плоскостями. Положение секущих плоскостей указывается штрихами линии сечения со стрелками, отмеченными одной и той же буквой. Эти штрихи принимаются за начальный и конечный штрихи линии сечения. Линия сечения имеет также перегибы, показывающие места перехода от одной секущей плоскости к другой. Перегибы линии сечения еще выполняются штрихами разомкнутой линии. Наличие перегибов в линии сечения не отражается на графическом оформлении ступенчатого разреза, линии перехода между секущими плоскостями не показывают.
Ломаными называются разрезы, полученные от рассечения предмета пересекающимися плоскостями. Секущие плоскости условно повертывают около линии взаимного пересечения до совмещения с плоскостью (рис. 3.13), параллельной какой-либо из основных плоскостей проекций, при этом линия поворота может не совпадать с направлением взгляда.
Если совмещенные плоскости окажутся параллельными одной из основных плоскостей проекций, то ломаный разрез допускается помещать на месте соответствующего вида (рис. 3,13).
Вместе с секущей плоскостью поворачивается расположенная в ней фигура сечения детали. На рис. 3.13 для наглядности нанесены линии связи, эти построения на чертеже не должны быть показаны.
При повороте секущей плоскости элементы предмета, расположенные за ней, вычерчивают так, как они проецируются на соответствующую плоскость, с которой производится совмещение.
Разрез, служащий для выявления формы предмета лишь в отдельном ограниченном месте, называется местным и отделяется от вида сплошной волнистой тонкой линией (рис. 3.14) или сплошной тонкой линией с изломом. Эти линии не должны совпадать с какими-либо линиями изображения.
Если местный разрез выполняется на части изображаемого предмета, представляющей собой симметричную фигуру (рис. 3.15), где разделяющей линией служит ось симметрии, то местный разрез с видом может разделяться этой осевой линией или линией обрыва.
Сечения
Сечением называется изображение фигуры, получающееся при мысленном рассечении предмета одной или несколькими плоскостями. Секущие плоскости нужно выбирать так, чтобы получились нормальные поперечные сечения. В отличие от разреза на сечении показывается только то, что расположено непосредственно в секущей плоскости, а все, что расположено за ней, не изображается (рис. 3,16).
Сечения, не входящие в состав разреза, разделяют на вынесенные и наложенные.
Вынесенные сечения располагаются на свободном поле чертежа и более предпочтительны для однозначного чтения чертежа. Контур вынесенного сечения, а также сечения, входящего в состав разреза, изображают сплошными основными линиями (рис. 3.16). Не обозначают вынесенные сечения, когда их располагают на линии сечения, если они имеют ось симметрии. При этом положение секущей плоскости показывают штрихпунктирной линией. В случае расположения сечения на свободном месте их обозначают аналогично разрезам (рис. 3.16, сечение А-А). Сечения необходимо обозначать, даже если они находятся в проекционной связи (рис. 3.16, сечение Б-Б).
Наложенные сечения располагаются непосредственно на изображении предмета (рис. 3.17, б, 3.18, б). Вынесенные сечения могут располагаться не только на свободном поле чертежа (рис. 3.16), но и в разрыве изображения предмета (рис. 3.17, а, 3.18, а). Вынесенное симметричное сечение может располагаться в непосредственной близости от изображения, причем его ось симметрии должна совпадать с положением секущей плоскости и пересекать контур изображения предмета.
На чертежах для несимметричных сечений, расположенных в разрыве (рис. 3.18, а) или наложенных сечениях (рис. 3.18, б), линии сечения обозначают разомкнутой линией со стрелкой, но нс буквами.
Несимметричное сечение по построению и расположению должно соответствовать направлению, указанному стрелками (рис. 3.18).
Контур выносного сечения, а также сечения, входящего в состав разреза, выполняется сплошной основной линией (толщиной 5), контур наложенного сечения выполняется сплошной тонкой линией (от S/2 до S/3), как показано на рис. 3.17, б и 3.18, б.
Выносные элементы
Дополнительное отдельное изображение какой-либо части фигуры, обычно увеличенное, требующее графического или других пояснений в отношении формы, размеров и иных данных, называется выносным элементом (рис. 3.19, 3.20).
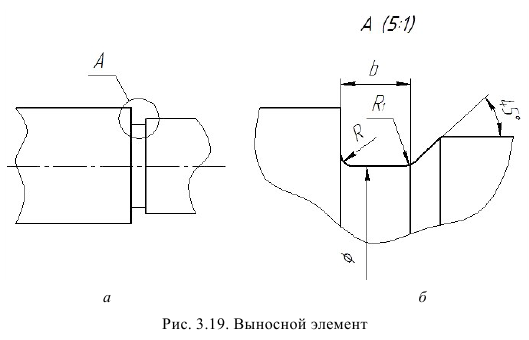
Рис. 3.19. Выносной элемент
При применении выносного элемента соответствующее место изображения отмечают замкнутой сплошной тонкой линией (окружностью или овалом) с обозначением выносного элемента прописной буквой русского алфавита или сочетанием прописной буквы с арабской цифрой на полке линии-выноски (рис. 3.19, а и 3.20, а).
Над выносным элементом (рис. 3.19, б и 3.20, б) указывается та же цифра и масштаб, в котором выполнен выносной элемент (масштабы могут быть различные).
Выносной элемент следует располагать как можно ближе к соответствующему месту на изображении предмета. Выносной элемент может содержать подробности, не указанные на соответствующем изображении, и отличаться от него по содержанию. Например, изображение может быть видом, а выносной элемент — разрезом.
Кстати вы всегда можете заказать чертежи.
Лекции по предметам:
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.







































































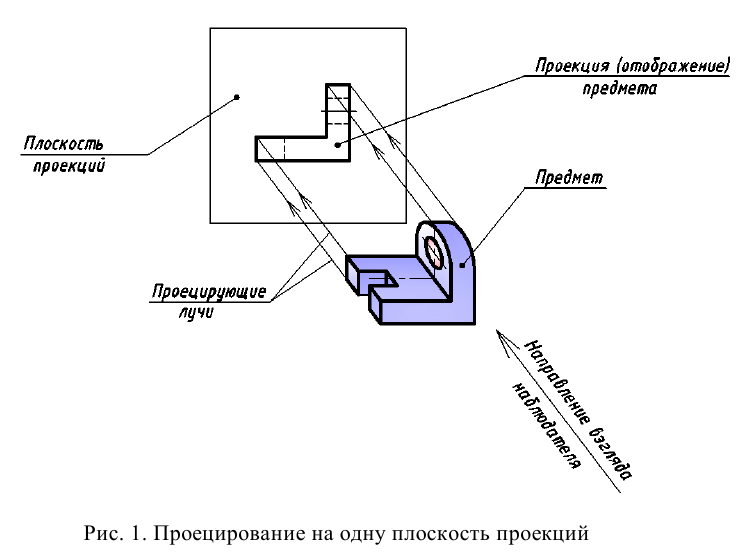
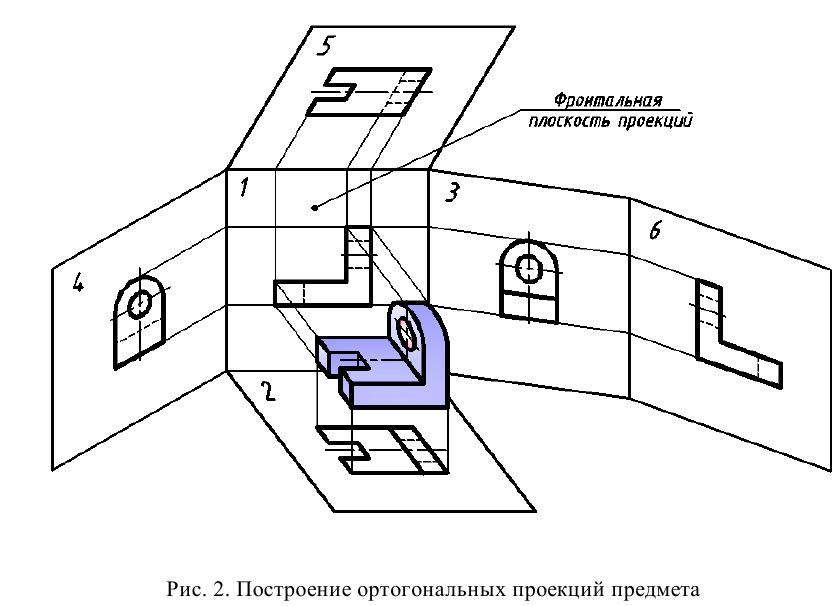
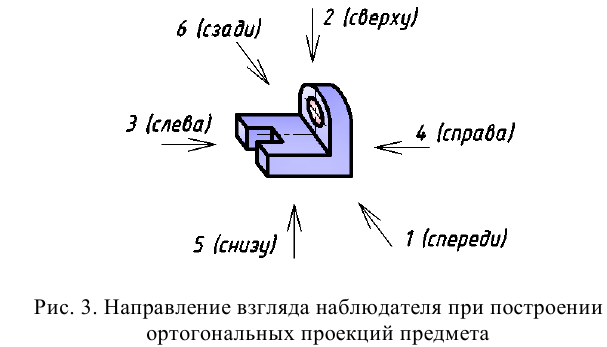
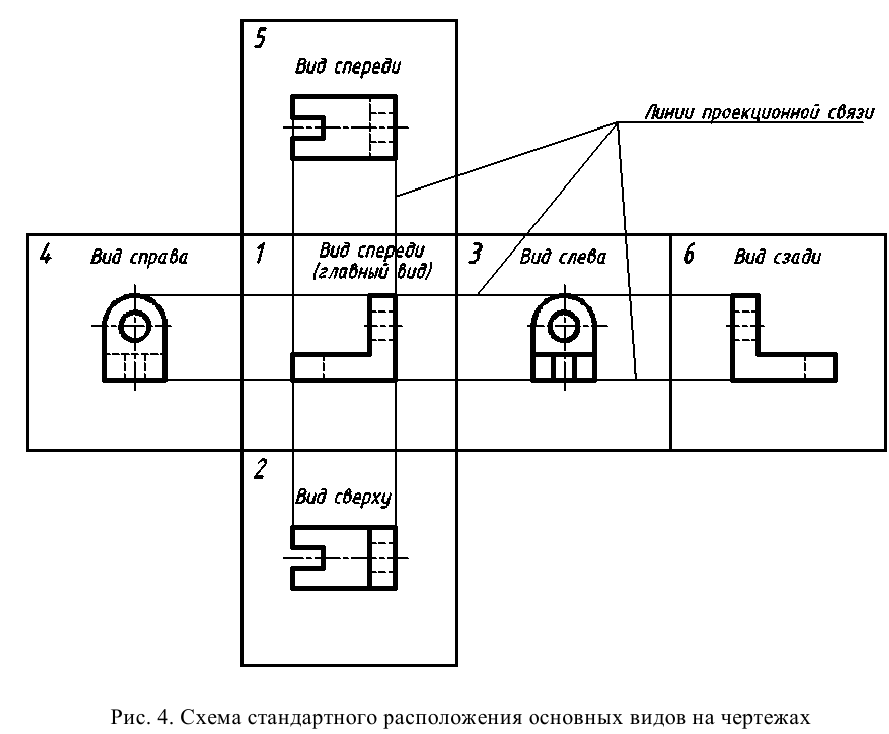
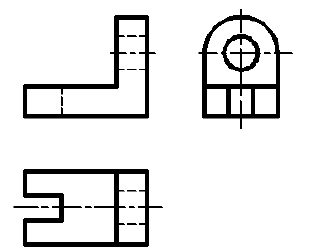
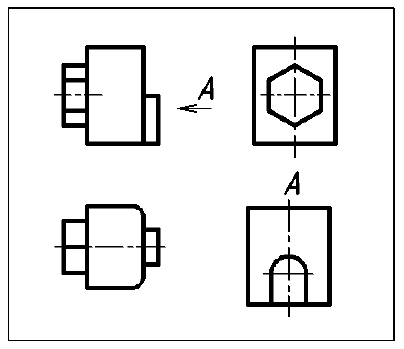
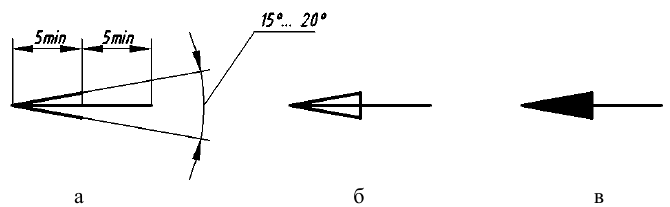
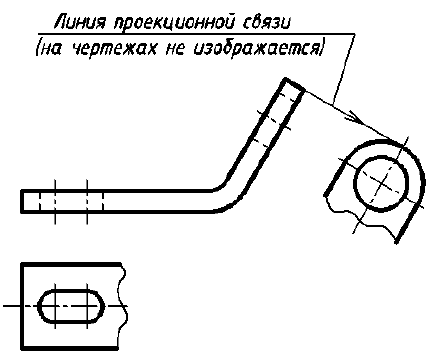
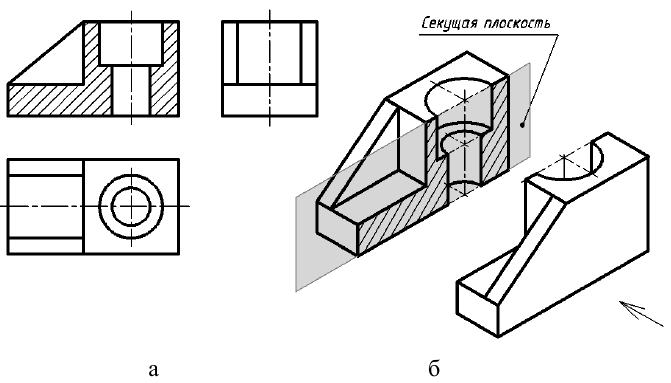
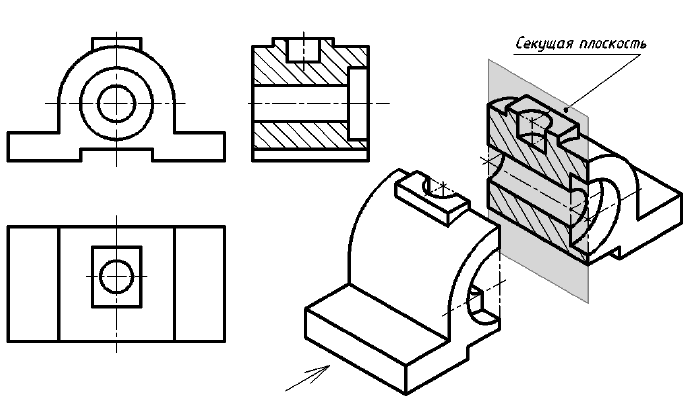
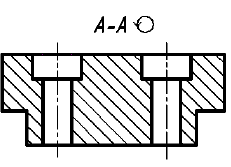
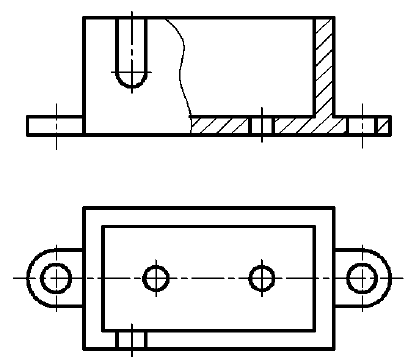
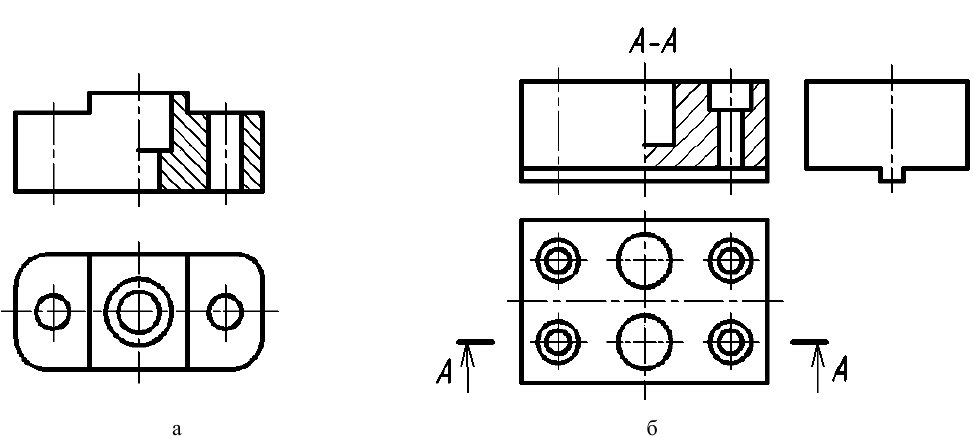
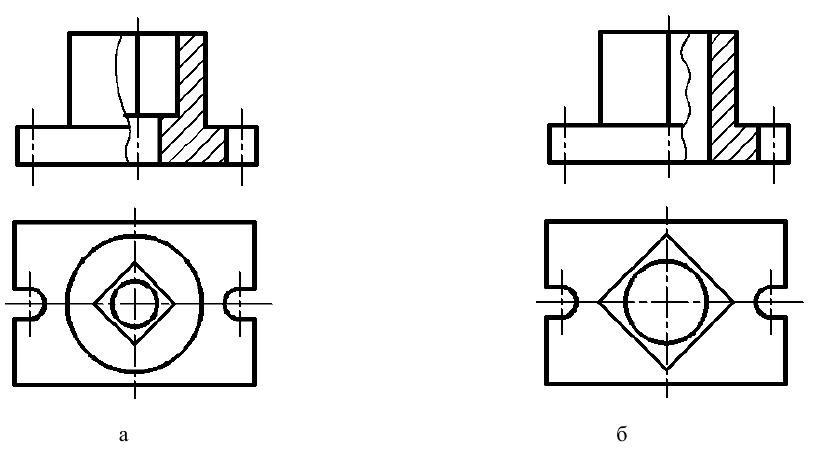
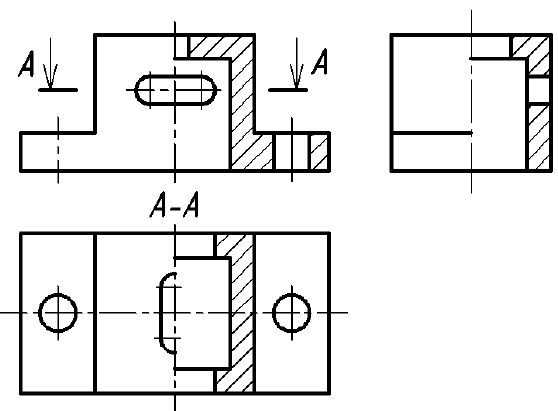
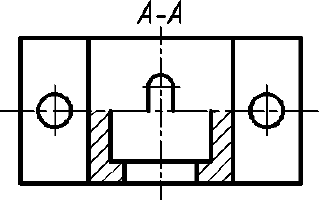
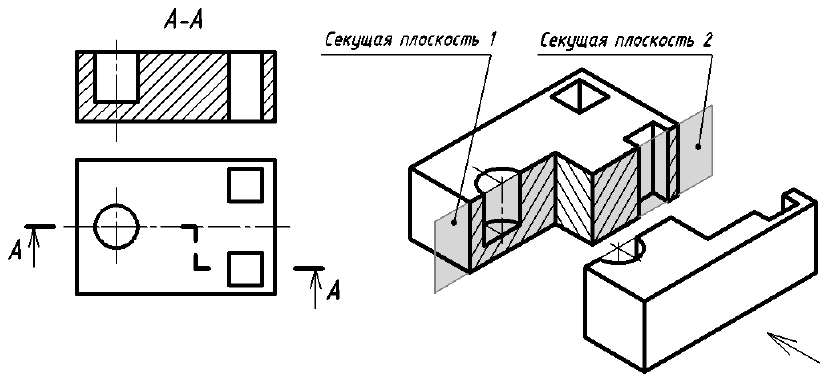
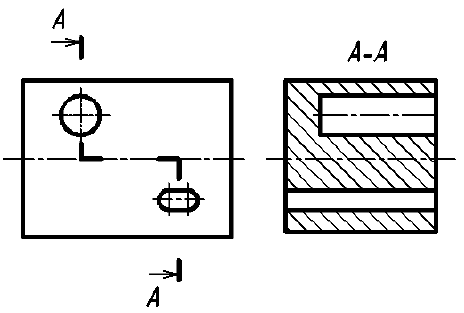
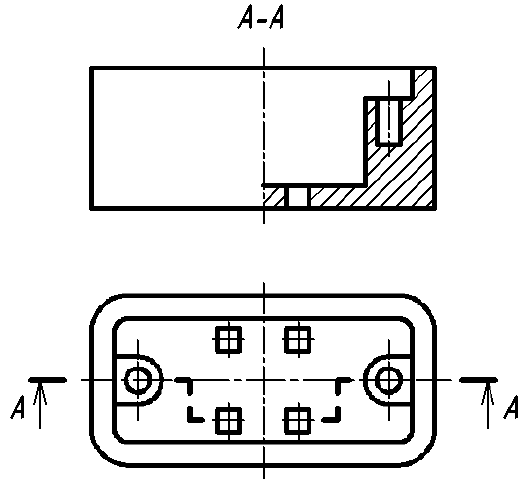
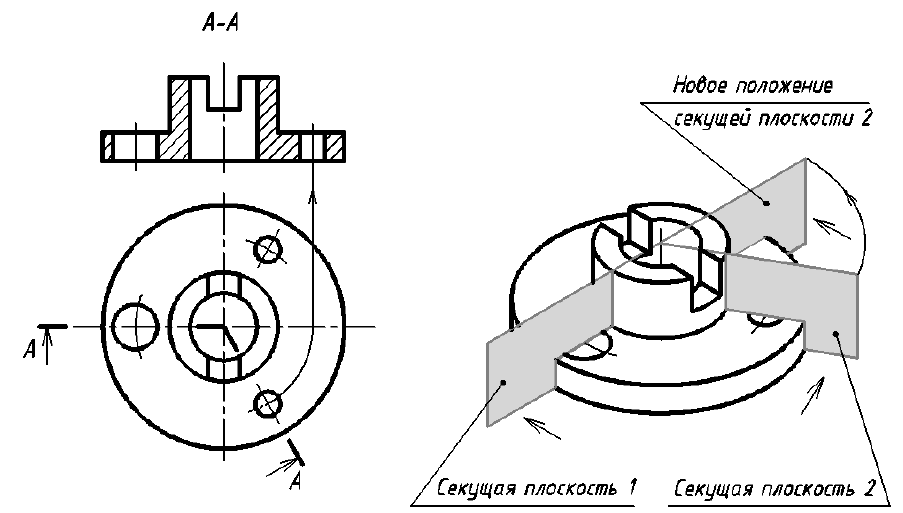
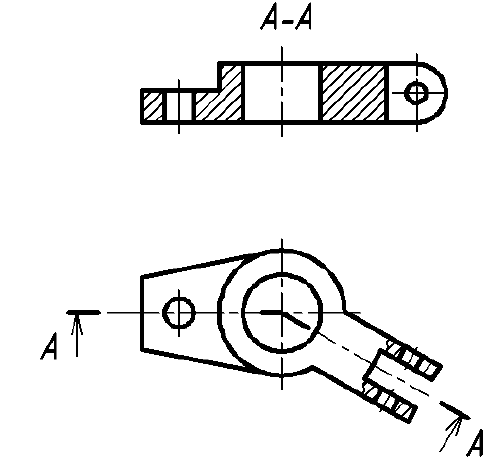
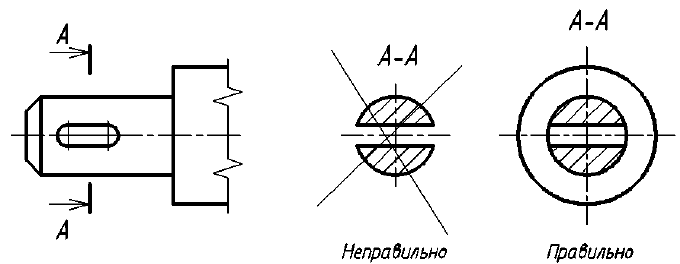
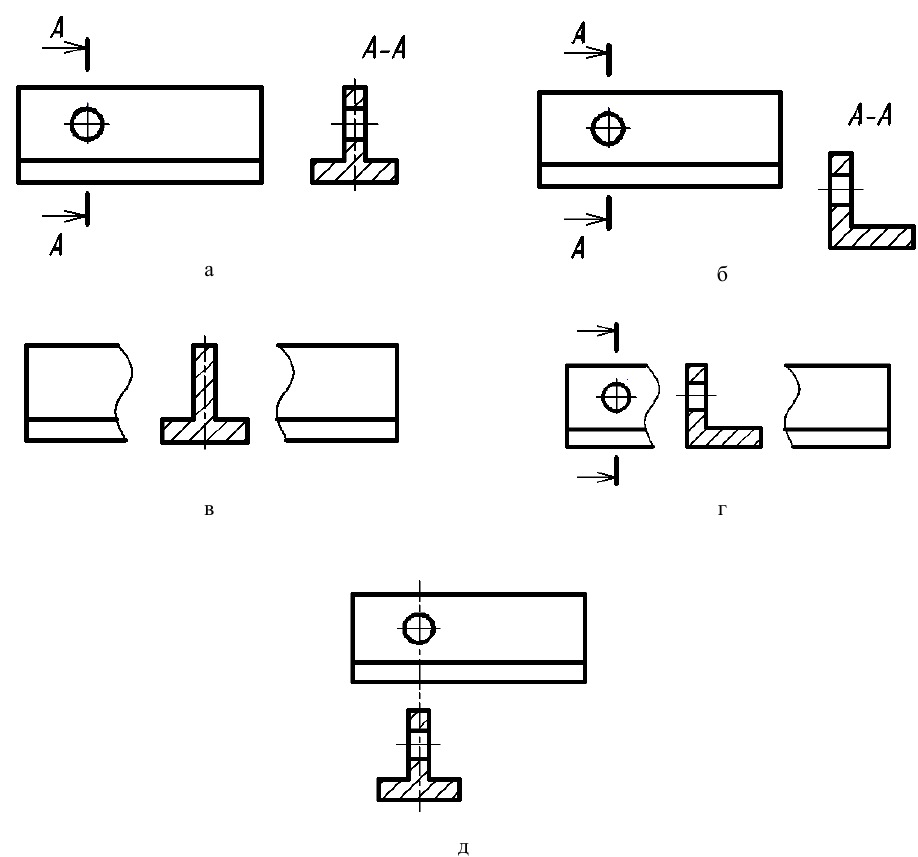
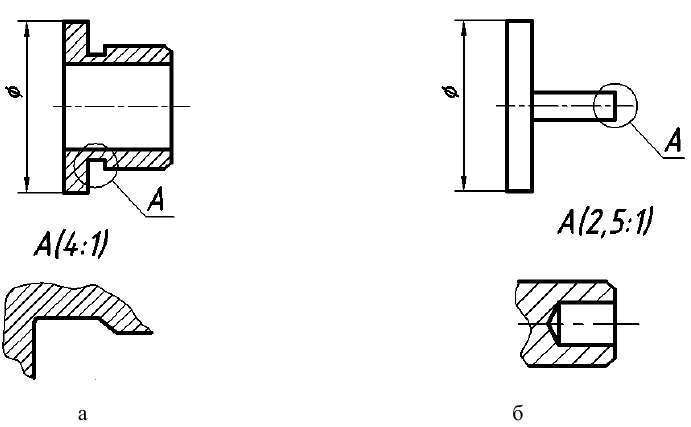
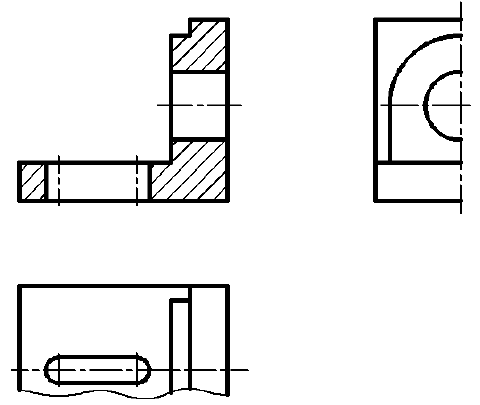
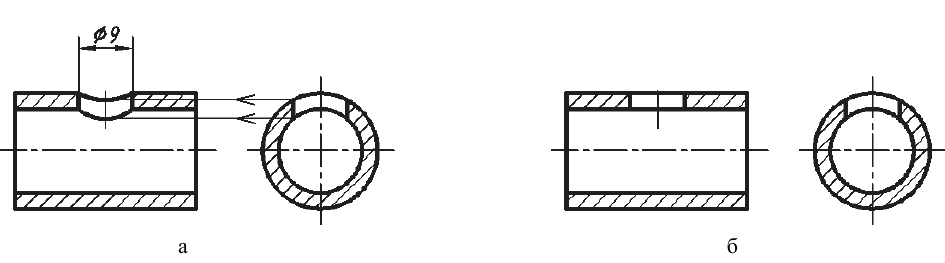
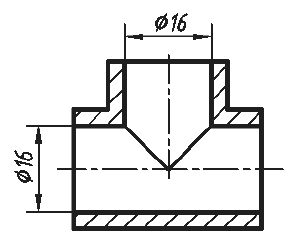
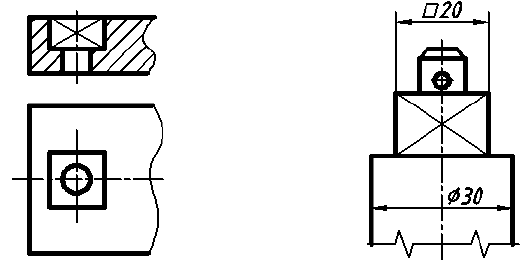
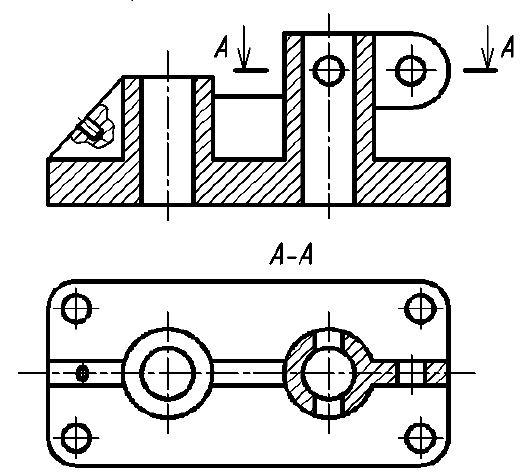
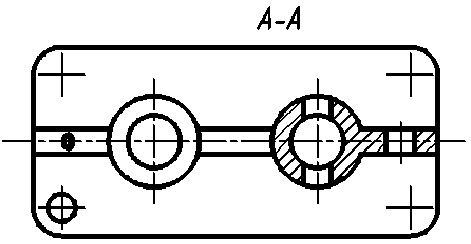
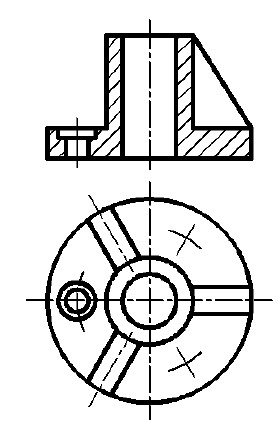
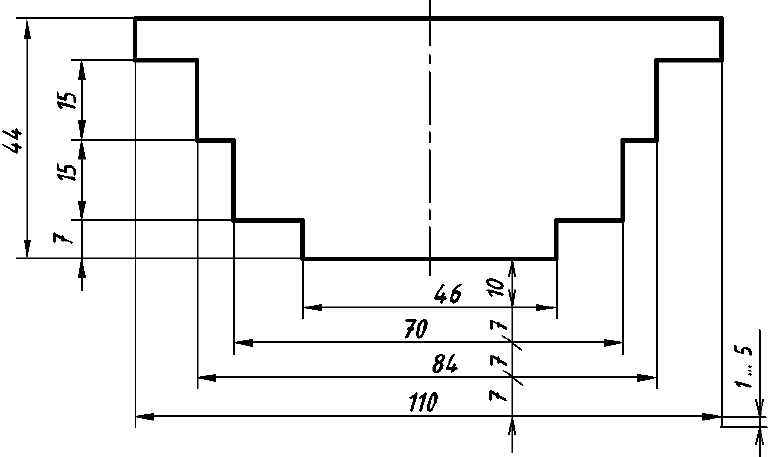
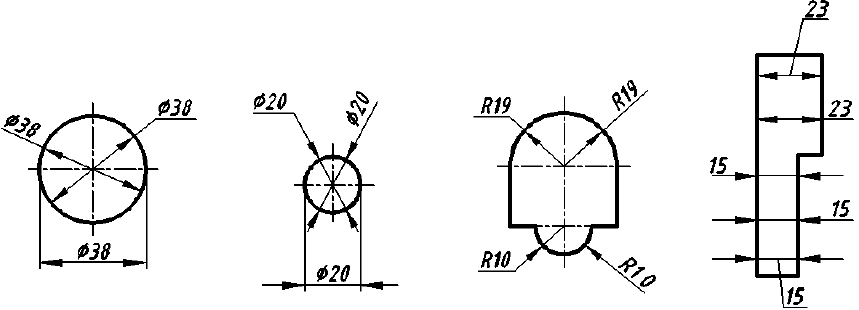
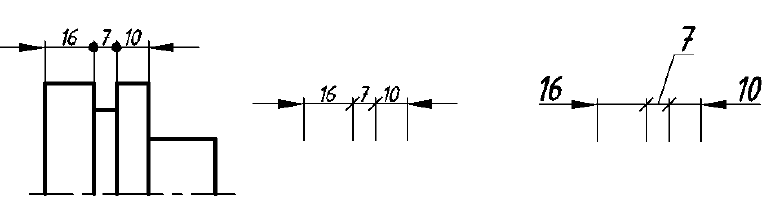
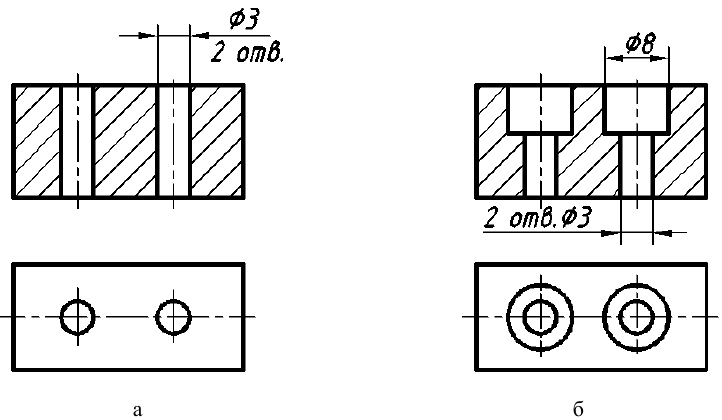
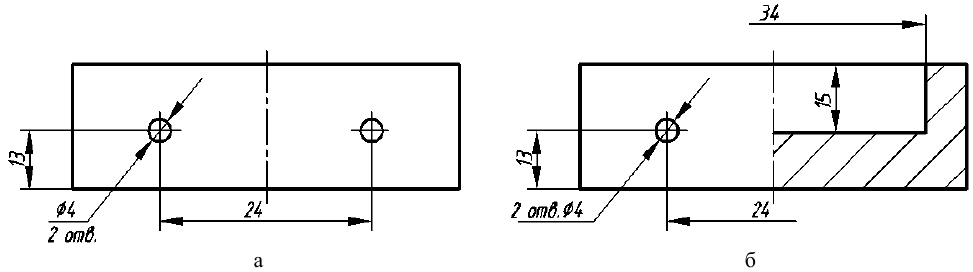
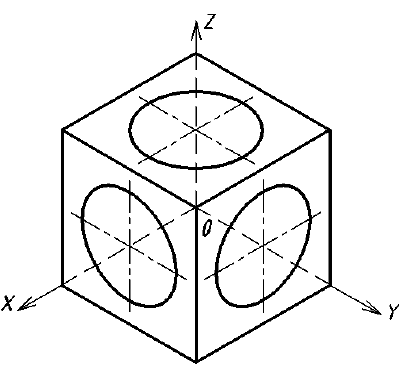
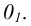 Проведем через нее изометрические оси X и Y (они параллельны сторонам верхней грани). Отложим в обе стороны от точки
Проведем через нее изометрические оси X и Y (они параллельны сторонам верхней грани). Отложим в обе стороны от точки 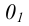 на каждой оси отрезки, равные радиусу окружности. Через полученные точки проведем прямые, параллельные осям. Получим ромб, представляющий изометрическую проекцию квадрата, в который вписана окружность.
на каждой оси отрезки, равные радиусу окружности. Через полученные точки проведем прямые, параллельные осям. Получим ромб, представляющий изометрическую проекцию квадрата, в который вписана окружность.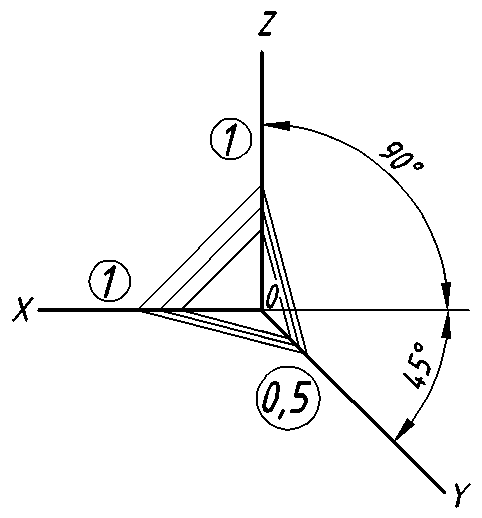
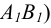 и малую (отрезок
и малую (отрезок 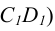 оси эллипса с центром в точке
оси эллипса с центром в точке 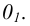
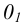 на продолжениях оси
на продолжениях оси 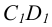 отрезки, равные диаметру исходной окружности d и определим точки
отрезки, равные диаметру исходной окружности d и определим точки 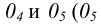 на рис. 66 не показана). Из точек
на рис. 66 не показана). Из точек 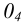 и
и 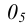 проведем дуги радиусом R =
проведем дуги радиусом R = 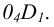
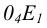 с большой осью эллипса
с большой осью эллипса 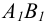 определим точку
определим точку 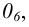 из которой радиусом
из которой радиусом 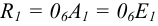 проведем левую дугу. Аналогично построим правую дугу.
проведем левую дугу. Аналогично построим правую дугу.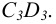
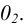
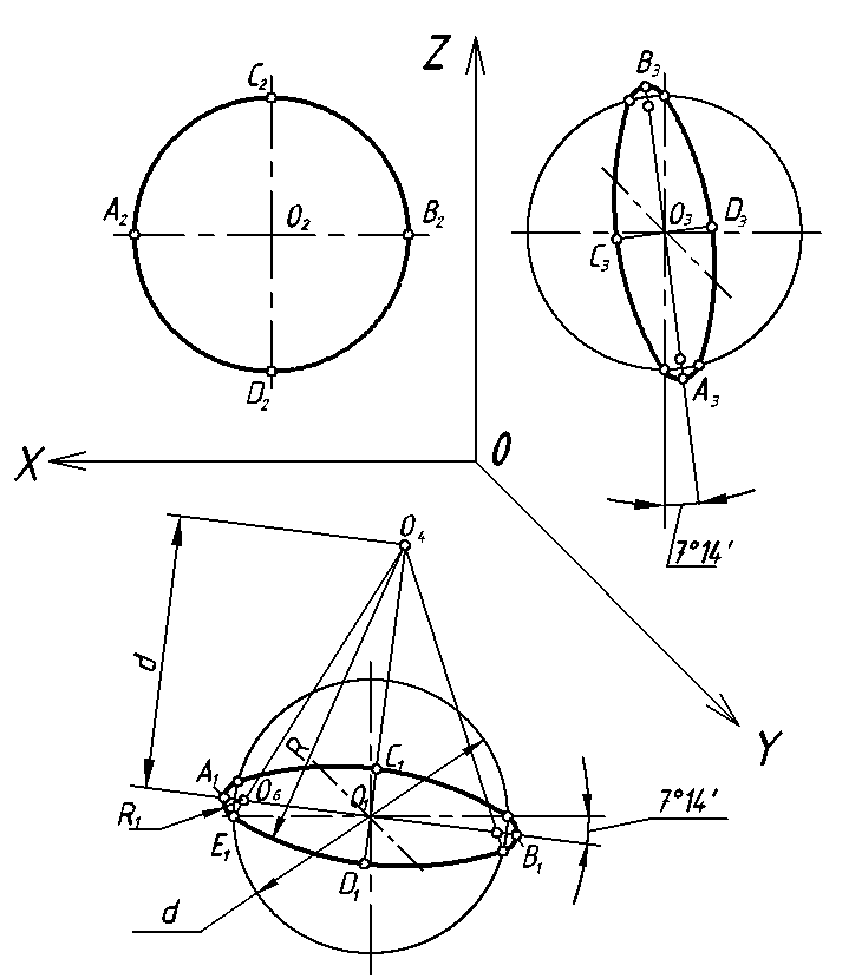
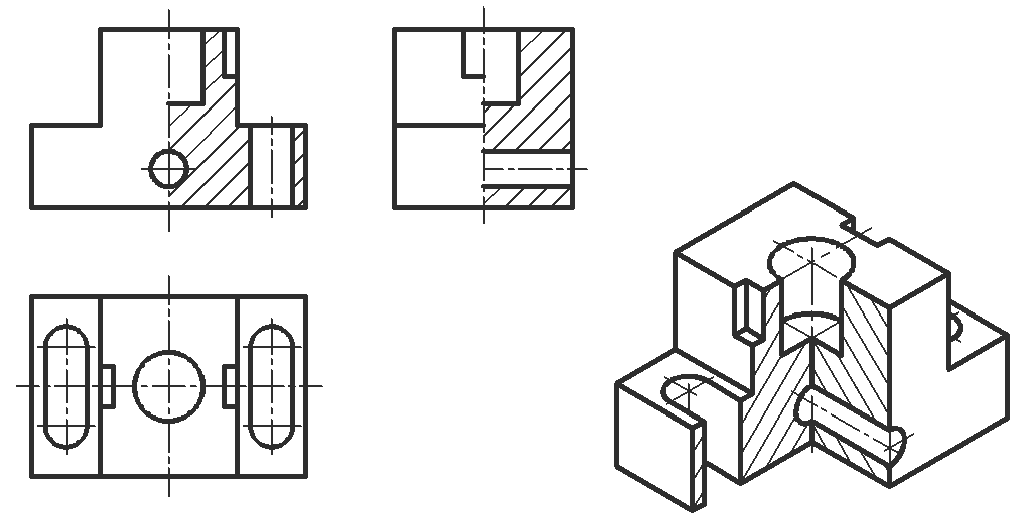
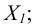
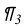 провести ось симметрии
провести ось симметрии 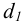 на расстоянии
на расстоянии 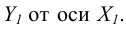 Это расстояние должно быть равно такому же
Это расстояние должно быть равно такому же 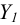 от оси симметрии d до оси проекций X (см. рис. 69, вид сверху);
от оси симметрии d до оси проекций X (см. рис. 69, вид сверху);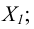
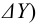 и отложить эти расстояния на линиях проекционной связи в обе стороны от оси
и отложить эти расстояния на линиях проекционной связи в обе стороны от оси 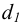 на плоскости
на плоскости 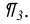 Отметить построенные точки;
Отметить построенные точки;