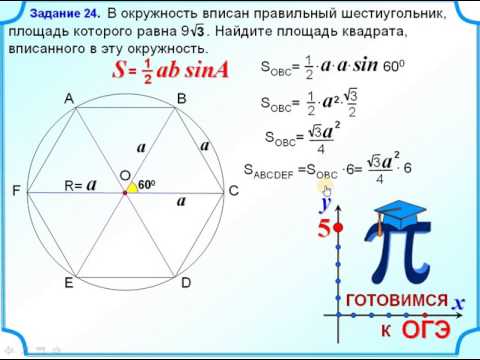
Знаете ли вы, как выглядит правильный шестиугольник?
Этот вопрос задан не случайно. Большинство учащихся 11 класса не знают на него ответа.
Правильный шестиугольник — такой, у которого все стороны равны и все углы тоже равны.
Железная гайка. Снежинка. Ячейка сот, в которых живут пчелы. Молекула бензола. Что общего у этих объектов? — То, что все они имеют правильную шестиугольную форму.
Многие школьники теряются, видя задачи на правильный шестиугольник, и считают, что для их решения нужны какие-то особые формулы. Так ли это?
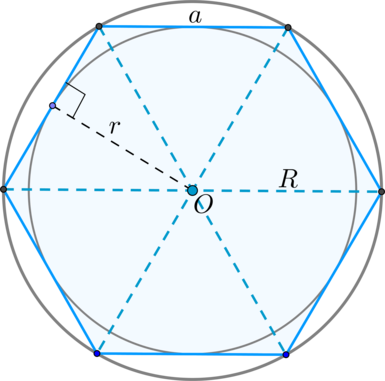
Проведем диагонали правильного шестиугольника. Мы получили шесть равносторонних треугольников.
Мы знаем, что площадь правильного треугольника: .
Тогда площадь правильного шестиугольника — в шесть раз больше.
, где — сторона правильного шестиугольника.
Обратите внимание, что в правильном шестиугольнике расстояние от его центра до любой из вершин одинаково и равно стороне правильного шестиугольник.
Значит, радиус окружности, описанной вокруг правильного шестиугольника, равен его стороне.
Радиус окружности, вписанной в правильный шестиугольник, нетрудно найти.
Он равен .
Теперь вы легко решите любые задачи ЕГЭ, в которых фигурирует правильный шестиугольник.
Ты нашел то, что искал? Поделись с друзьями!
. Найдите радиус окружности, вписанной в правильный шестиугольник со стороной .
Радиус такой окружности равен .
. Чему равна сторона правильного шестиугольника, вписанного в окружность, радиус которой равен 6?
Мы знаем, что сторона правильного шестиугольника равна радиусу описанной вокруг него окружности.
Видео:9 класс, 24 урок, Формулы для вычисления площади правильного многоугольника, его стороныСкачать

Сторона правильного шестиугольника. Калькулятор и формулы
Определить сторону правильного шестиугольника можно легко при помощи этого калькулятора. Просто заполните любую ячейку, введя известное вам значение, – и под калькулятором отобразятся значения всех недостающих величин, а также формулы их нахождения. Это удобная шпаргалка по геометрии, которую полезно всегда держать под рукой!
Введите данные:
Достаточно ввести только одно значение, остальное калькулятор посчитает сам.
Видео:Формулы радиусов описанной и вписанной окружностей правильного многоугольника 2Скачать

Правильный шестиугольник и его свойства
Определение
Выпуклый многоугольник называется правильным, если все его стороны равны и все его углы равны.
Замечание
Т.к. сумма всех углов (n) –угольника равна (180^circ(n-2)) , то каждый угол правильного (n) –угольника равен [alpha_n=dfracn cdot 180^circ]
Пример
Каждый угол правильного четырехугольника (т.е. квадрата) равен (dfrac 4cdot 180^circ=90^circ) ;
каждый угол правильного шестиугольника равен (dfrac6cdot 180^circ=120^circ) .
Теоремы
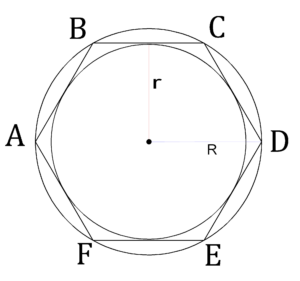
1. Около любого правильного многоугольника можно описать окружность, и притом только одну.
2. В любой правильный многоугольник можно вписать окружность, и притом только одну.
Следствия
1. Окружность, вписанная в правильный многоугольник, касается всех его сторон в серединах.
2. Центры вписанной и описанной окружности у правильного многоугольника совпадают.
Теорема
Если (a) – сторона правильного (n) –угольника, (R) и (r) – радиусы описанной и вписанной окружностей соответственно, то верны следующие формулы: [begin S&=dfrac n2ar\ a&=2Rcdot sindfracn\ r&=Rcdot cosdfracn end]
Свойства правильного шестиугольника
1. Сторона равна радиусу описанной окружности: (a=R) .
2. Радиус описанной окружности является биссектрисой угла правильного шестиугольника.
3. Все углы правильного шестиугольника равны (120^circ) .
4. Площадь правильного шестиугольника со стороной (a) равна (dfrac<3sqrt>a^2) .
5. Диагонали пересекаются в одной точке и делят его на 6 равносторонних треугольников, у которых высота равна радиусу (r) вписанной в правильный шестиугольник окружности.
6. Инвариантен относительно поворота плоскости на угол, кратный (60^circ) относительно центра описанной окружности (слово “инвариантный” означает, что при таких поворотах правильный шестиугольник перейдёт в себя, то есть такие повороты являются его симметриями).
Замечание
В общем случае правильный (n) -угольник инвариантен относительно поворота на угол (dfrac) .
📸 Видео
Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Формулы для вычисления площади правильного многоугольника,его стороны и радиуса вписанной окружностиСкачать

Геометрия 9 класс (Урок№22 - Формулы площади правильного многоугольника,стороны и радиуса впис.окр.)Скачать

9 класс, 22 урок, Окружность, описанная около правильного многоугольникаСкачать

Задача 6 №27916 ЕГЭ по математике. Урок 133Скачать

112. Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписаннойСкачать

Формулы для вычисления площади правильного многоугольника,его стороны и радиуса вписанной окружностиСкачать

Как построить шестиугольник вписанный в окружностьСкачать

ЕГЭ ПЛАНИМЕТРИЯ В ЕРЕВАНЕ НАХОЖДЕНИЕ СТОРОН ПРАВИЛЬНОГО ШЕСТИУГОЛЬНИКА ВПИСАННОГО В ОКРУЖНОСТЬ |Скачать

Геометрия 9 класс (Урок№21 - Правильный многоугольник. Описанная и вписанная окружность.)Скачать

Свойства правильного шестиугольника. Сравнение площадей. Разбор задачи из стереометрии.Скачать

151 Диагонали правильного шестиугольника пересекаются в центре его описанной окружности (268)Скачать

Геометрия - Построение шестиугольникаСкачать

Вписанная и описанная окружность - от bezbotvyСкачать

Задача 6 №27909 ЕГЭ по математике. Урок 129Скачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

9 класс, 23 урок, Окружность, вписанная в правильный многоугольникСкачать

Задание 24 Правильный шестиугольник вписан в окружностьСкачать