Формула расчета длины окружности основания цилиндра

В данной публикации мы рассмотрим, как можно найти площадь поверхности цилиндра и разберем примеры решения задач для закрепления материала.

Видео:№537. Диаметр основания цилиндра равен 1 м, высота цилиндра равна длинеСкачать

Формула вычисления площади цилиндра

1. Боковая поверхность

Площадь (S) боковой поверхности цилиндра равна произведению длины окружности, являющейся основанием фигуры, на его высоту.

Длина окружности, в свою очередь, рассчитывается так: C = 2 π R. Следовательно, рассчитать площадь можно следующим образом:

S = 2 π R h

Примечание: в вычислениях значение числа π округляется до 3,14.

2. Основание

В качестве оснований цилиндра (равны между собой), выступает круг, площадь которого равна:

S = π R 2

Т.к. диаметр круга равен двум его радиусам (d = 2R), выражение можно преобразовать таким образом:

3. Полная площадь

Для нахождения данной величины необходимо просуммировать площади боковой поверхности и двух равных оснований цилиндра, т.е.:

S = 2 π R h + 2 π R 2 или S = 2 π R (h + R)

Видео:Цилиндр - расчёт площади, объёма.Скачать

Примеры задач

Задание 1
Найдите площадь боковой поверхности цилиндра, если его радиус равен 11 см, а высота – 8 см.

Решение:
Воспользуемся первой формулой, подставив в нее данные по условиям задачи значения:
S = 2 ⋅ 3,14 ⋅ 11 см ⋅ 8 см = 552,64 см 2 .

Задание 2
Высота цилиндра равна 9 см, а его диаметр – 8 см. Найдите суммарную площадь поверхности фигуры.

Решение:
Если диаметр цилиндра равен 8 см, значит его радиус составляет 4 см (8 см / 2). Применив соответствующую формулу для нахождения площади получаем:
S = 2 ⋅ 3,14 ⋅ 4 см ⋅ (9 см + 4 см) = 326,56 см 2 .

Видео:Объём цилиндраСкачать

Геометрические тела. Цилиндр.

Цилиндр − это геометрическое тело, которое ограничено цилиндрической поверхностью и 2-мя плоскостями, которые параллельны и пересекают ее.

ABCDEFG и abcdefg — это основания цилиндра. Расстояние между основаниями (KM) – высота цилиндра.

Цилиндрические сечения боковой поверхности кругового цилиндра.

Сечения, которые идут параллельно к основанию, будут являться кругами одного радиуса. Сечения, которые параллельны образующим цилиндра — это пары параллельных прямых (AB || CD). Сечения, не параллельные ни основанию, ни образующим, являются эллипсами.

Цилиндрическая поверхность образуется посредством движения прямой параллельно самой себе. Точка прямой, которая выделена, перемещается вдоль заданной плоской кривой – направляющей. Эта прямая называется образующей цилиндрической поверхности.

Прямой цилиндр – это такой цилиндр, в котором образующие перпендикулярны основанию. Если образующие цилиндра не перпендикулярны основанию, то это будет наклонный цилиндр.

Круговой цилиндр – цилиндр, основанием которого является круг.

Круглый цилиндр – такой цилиндр, который одновременно и прямой, и круговой.

Прямой круговой цилиндр определяется радиусом основания R и образующей L, которая равна высоте цилиндра H.

Призма – это частный случай цилиндра.

Видео:11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать

Формулы нахождения элементов цилиндра.

Площадь боковой поверхности прямого кругового цилиндра:

Площадь полной поверхности прямого кругового цилиндра:

Объем прямого кругового цилиндра:

Прямой круговой цилиндр со скошенным основанием либо кратко скошенный цилиндр определяют с помощью радиуса основания R, минимальной высоты h₁ и максимальной высоты h₂.

Площадь боковой поверхности скошенного цилиндра:

Площадь оснований скошенного цилиндра:

Площадь полной поверхности скошенного цилиндра:

Объем скошенного цилиндра:

L — образующая цилиндра;

H — высота цилиндра;

S_бок — площадь боковой поверхности;

Видео:Длина окружности. Площадь круга. 6 класс.Скачать

Длина окружности основания цилиндра это

Видео:КАК ИЗМЕРИТЬ ДЛИНУ ОКРУЖНОСТИ? · ФОРМУЛА + примеры · Длина окружности как найти? Математика 6 классСкачать

Как находится длина окружности основания цилиндра

Видео:Длина окружности. Математика 6 класс.Скачать

Нахождение радиуса цилиндра: формула и примеры

В данной публикации мы рассмотрим, как можно вычислить радиус цилиндра и разберем примеры решения задач для закрепления материала.

Видео:Длина окружности. Площадь круга - математика 6 классСкачать

Формулы вычисления радиуса цилиндра

1. Через объем и высоту

Радиус цилиндра рассчитывается по формуле:

V – объем цилиндра; считается как произведение числа π на высоту фигуры на квадрат радиуса круга, являющего ее основанием.

• R – радиус основания цилиндра, т.е. окружности;
• π – число, округленное значение которого равняется 3,14.

2. Через площадь боковой поверхности

Радиус цилиндра считается таким образом:

S_бок. – площадь боковой поверхности цилиндра; равна произведению длины окружности (2 π R), являющейся основанием фигуры, на его высоту:

3. Через полную площадь поверхности

Данная формула получена следующим образом:

S – полная площадь поверхности фигуры, равная:

S = 2 π Rh + 2 π R 2 или S = 2 π R(h + R)

Возьмем первое выражение. Если перенести S в правую часть, получим:

2 π R 2 + 2 π Rh – S = 0

Можно заметить, что это квадратное уравнение вида ax 2 + bx + c = 0, где:

R является корнем данного уравнения (x). Подставив в стандартную формулу для расчета корней наши значения a, b и с получаем*:

* в нашем случае – только один положительный корень, т.к. радиус не может быть отрицательным.

Видео:Цилиндр, конус, шар, 6 классСкачать

Примеры задач

Задание 1
Высота цилиндра равняется 5 см, а объем – 141,3 см 3 . Вычислите его радиус.

Решение:
Воспользуемся соответствующей формулой, подставив в нее известные по условиям задачи значения:

Задание 2
Найдите радиус цилиндра, если площадь его боковой поверхности равна 175,84 см 2 , а высота составляет 7 см.

Решение:
Применим формулу, в которой задействованы заданные величины:

Задание 3
Рассчитайте радиус цилиндра, если полная площадь его поверхности – 602,88 см 2 , а высота – 10 см.

Решение:
Используем третью формулу для нахождения неизвестной величины:

Видео:Видеоурок по математике "Цилиндр"Скачать

Что такое цилиндр: определение, элементы, виды, варианты сечения

В данной публикации мы рассмотрим определение, основные элементы, виды и возможные варианты сечения одной из самых распространенных трехмерных геометрических фигур – цилиндра. Представленная информация сопровождается наглядными рисунками для лучшего восприятия.

Видео:11 класс. Геометрия. Объем цилиндраСкачать

Определение цилиндра

Далее мы подробно остановимся на прямом круговом цилиндре как самой популярной разновидности фигуры. Другие ее виды будут перечислены в последнем разделе данной публикации.

Прямой круговой цилиндр – это геометрическая фигура в пространстве, полученная путем вращения прямоугольника вокруг своей стороны или оси симметрии. Поэтому такой цилиндр иногда называют цилиндром вращения.

Цилиндр на рисунке выше получен в результате вращения прямоугольного треугольника ABCD вокруг оси O₁O₂ на 180° или прямоугольников ABO₂O₁/O₁O₂CD вокруг стороны O₁O₂ на 360°.

Видео:+Как найти длину окружностиСкачать

Основные элементы цилиндра

• Основания цилиндра – два одинаковых по размеру/площади круга с центрами в точках O₁ и O₂.
• R – радиус оснований цилиндра, отрезки AD и BC – диаметры (d).
• O₁O₂ – ось симметрии цилиндра, одновременно является его высотой (h).
• l (AB, CD) – образующие цилиндра и одновременно с этим стороны прямоугольника ABCD. Равны высоте фигуры.

Развёртка цилиндра – боковая (цилиндрическая) поверхность фигуры, развернутая в плоскость; является прямоугольником.

• длина данного прямоугольника равна длине окружности основания цилиндра ( 2πR );
• ширина равна высоте/образующей цилиндра.

Примечание: формулы для нахождения площади поверхности и объема цилиндра представлены в отдельных публикациях.

Видео:Лучший способ найти площадь кругаСкачать

Длина окружности основания цилиндра это

Если секущая плоскость пересекает ось цилиндра и не перпендикулярна ей, то в сечении может получиться эллипс (рис. 145) или его некоторая часть (рис. 146, 147). Это следует из того, что параллельной проекцией окружности на плоскость, не параллельную плоскости окружности, является эллипс. ( Вспомните : наклонив цилиндрический стеклянный сосуд с водой, вы видите на поверхности воды эллипс или его часть. )

Сечение цилиндра плоскостью, проходящей через ось, называется осевым сечением цилиндра. Так как поворот пространства вокруг прямой на угол 180 ° является осевой симметрией относительно оси вращения, то ось прямого кругового цилиндра является его осью симметрии. Значит, осевым сечением цилиндра вращения является прямоугольник, стороны которого равны диаметру основания и образующей цилиндра (рис. 148). При этом все осевые сечения цилиндра — равные между собой прямоугольники .

Цилиндр, осевое сечение которого — квадрат, называют равносторонним цилиндром (рис. 149).

Так как все образующие цилиндра равны и параллельны друг другу, то любое сечение цилиндра плоскостью, параллельной его оси, есть прямоугольник, высота которого равна образующей цилиндра (рис. 150).

б) Изображение цилиндра. Чтобы построить изображение цилиндра, достаточно построить: 1) прямоугольник AВB 1 A 1 и его ось OO 1 (рис. 151); 2) два равных эллипса, центрами которых являются точки O и O 1 и осями — отрезки АВ и A 1 В 1 . Выделив штрихами невидимые линии, получаем искомое изображение цилиндра.

в) Касательная плоскость к цилиндру.

Определение. Плоскость, проходящая через образующую цилиндра перпендикулярно плоскости осевого сечения, проведённой через эту образующую, называется касательной плоскостью к цилиндру (рис. 152).

Говорят, что плоскость α касается цилиндра ( цилиндрической поверхности ) по образующей DD 1 , каждая точка образующей DD 1 является точкой касания плоскости α и данного цилиндра.

Через любую точку боковой поверхности цилиндра проходит только одна его образующая. Через эту образующую можно провести только одно осевое сечение и только одну плоскость, перпендикулярную плоскости этого осевого сечения. Следовательно, через каждую точку боковой поверхности цилиндра можно провести лишь одну плоскость, касательную к данному цилиндру в этой точке.

17.3. Развёртка и площадь поверхности цилиндра

Следует заметить, что развёртка поверхности вращения — понятие в определённой мере интуитивное. К тому же не для каждой поверхности тела вращения можно построить её развёртку. Иными словами, не каждую поверхность можно «развернуть» на плоскости. Например, не существует развёртки сферы (см. раздел «Дифференциальная геометрия» в конце этой книги).

Развёртку цилиндра мы также введём на интуитивном уровне.

Пусть R — радиус основания, h — высота цилиндра.

Полная поверхность цилиндра состоит из его боковой поверхности и двух оснований — равных кругов. Если эту поверхность «разрезать» по образующей DD 1 (рис. 153) и по окружностям оснований, затем боковую поверхность развернуть на плоскости, то получим развёртку полной поверхности цилиндра (рис. 154), состоящую из прямоугольника и двух равных кругов, касающихся противоположных сторон этого прямоугольника (рис. 155).

Попробуйте изготовить развёртку цилиндра и склеить из неё цилиндр.

За площадь боковой поверхности цилиндра принимается площадь её развёртки , т. е. площадь боковой поверхности цилиндра равна площади прямоугольника, у которого одна сторона равна длине окружности основания цилиндра, а другая сторона — высоте цилиндра:

Таким образом, доказана следующая теорема.

Теорема 26. Площадь боковой поверхности цилиндра равна произведению длины окружности основания на высоту. ▼

Площадь круга радиуса R равна π R 2 , поэтому S осн = π R 2 . Тогда для нахождения площади полной поверхность цилиндра справедливо:

S полн = S бок + 2 S осн = 2 π Rh + 2 π R 2 = 2 π R ( R + h ) .

Следствие. Пусть цилиндр образован вращением прямоугольника ABCD вокруг его высоты AD (рис. 156) . Тогда

S бок = 2 π DC • BC . (1)

Если EF — серединный перпендикуляр к образующей BC, проведённый из точки F оси l цилиндра, то EF = CD. Учитывая, что ВС = AD, получаем: S бок = 2 π EF • AD, т. е. боковая поверхность цилиндра равна произведению высоты цилиндра на длину окружности, радиус которой равен длине серединного перпендикуляра его образующей, проведённого из точки оcu цилиндра.

Это следствие найдёт своё применение в п. 19.7.

17 . 4 . Призмы, вписанные в цилиндр и описанные около цилиндра

Нам предстоит решать задачи, в которых рассматриваются многогранники, вписанные в фигуры вращения и описанные около них.

Для правильного и наглядного изображения конфигураций из таких многогранников и фигур вращения необходимо верно изображать правильные многоугольники, вписанные в окружность (круг) или описанные около неё.

Определение. Призма называется вписанной в цилиндр, если основания призмы вписаны в основания цилиндра (рис. 157).

Цилиндр в этом случае называют описанным около призмы.

Боковые рёбра призмы соединяют соответственные вершины её оснований, вписанных в основания цилиндра. Эти вершины лежат на окружностях оснований цилиндра. Образующие цилиндра соединяют соответственные точки окружностей его оснований и параллельны боковым рёбрам призмы. Следовательно, боковые рёбра вписанной в цилиндр призмы — образующие цилиндра.

Определение. Призма называется описанной около цилиндра, если основания призмы описаны около оснований цилиндра.

Цилиндр при этом называют вписанным в призму (рис. 158).

Так как соответственные стороны оснований призмы параллельны друг другу и перпендикулярны радиусам оснований цилиндра, проведённым в точки касания, то плоскости боковых граней призмы являются касательными плоскостями к цилиндру: эти плоскости касаются поверхности цилиндра по образующим , соединяющим точки, в которых стороны оснований призмы касаются окружностей оснований цилиндра.

При изображении правильных призм, вписанных в цилиндр, следует руководствоваться алгоритмами построений изображений правильных многоугольников, вписанных в окружность.

Итак, для построения изображения правильной призмы, вписанной в цилиндр: 1) строим изображение цилиндра; 2) строим изображение правильного многоугольника, вписанного в верхнее основание цилиндра; 3) через вершины построенного вписанного многоугольника проводим образующие цилиндра; 4) в нижнем основании цилиндра последовательно соединяем концы этих образующих; 5) выделяем видимые и невидимые линии (отрезки) изображаемых фигур.

На рисунке 159 изображены вписанные в цилиндр: призма, в основании которой прямоугольный треугольник (рис. 159, а ); правильная четырёхугольная призма (рис. 159, б ); правильная треугольная призма (рис. 159, в ); правильная шестиугольная призма (рис. 159, г ).

 ЗАДАЧА (3.029). Диагональ осевого сечения равностороннего цилиндра равна a . Найти площади боковой и полной поверхностей правильной призмы, вписанной в этот цилиндр, если призма: а) треугольная; б) четырёхугольная; в) шестиугольная.

Решени е. Рассмотрим случай а). Пусть в равносторонний цилиндр вписана правильная призма ABCA 1 B 1 C 1 (рис. 160); CDD 1 C 1 — осевое сечение; OO 1 = h — высота цилиндра; ОС = R — радиус основания цилиндра.

Так как цилиндр — равносторонний, то CDD 1 C 1 — квадрат, значит, высота цилиндра равна диаметру его основания. Тогда в квадрате СDD 1 С 1 находим CD = = a = h.

Далее, △ АВС — правильный, вписанный в основание, радиус которого R = = . Значит, сторона АВ и высота СЕ этого треугольника равны: АВ = R = , СЕ = R = a. Откуда

S осн = = ;
S бок = 3 S ABB 1 A 1 = 3 AB • BB 1 = 3 • • a = .

S полн = S бок + 2 S осн = + 2 • = .

Ответ: a) ; .

 ЗАДАЧА (3.032). В равносторонний цилиндр, высота которого равна a, вписана правильная призма. Найти расстояние и угол между диагональю боковой грани призмы и осью цилиндра, если призма: а) треугольная; б) четырёхугольная; в) шестиугольная.

Решени е. Рассмотрим случай б). Пусть ABCDA 1 B 1 C 1 D 1 — вписанная в цилиндр правильная призма (рис. 161). Найдём расстояние и угол между осью OO 1 цилиндра и скрещивающейся с ней (почему?) диагональю АB 1 боковой грани ABB 1 A 1 данной призмы.

Расстояние между скрещивающимися прямыми равно расстоянию между параллельными плоскостями, проведёнными через эти прямые.

Если точка Е — середина отрезка AD, то расстояние между скрещивающимися прямыми AB 1 и OO 1 равно расстоянию между плоскостью грани ABB 1 A 1 и параллельной ей (почему?) плоскостью сечения EFF 1 E 1 . Это расстояние равно длине отрезка ОK (где точка K — середина АВ ), так как OK ⟂ ( ABB 1 ) и ( ABB 1 ) || ( EFF 1 ) .

Поскольку данный цилиндр — равносторонний, то BDD 1 B 1 — квадрат со стороной BD = ВВ 1 = a. Тогда АВ = = . Значит, ОK = АЕ = = — искомое расстояние между прямыми ОО 1 и АВ 1 .

Обозначим ∠ ( OO 1 ; AB 1 ) = ϕ , M = AB 1 ∩ A 1 B. Для нахождения угла ϕ проведём в грани ABB 1 A 1 прямую KK 1 || OO 1 . Тогда ϕ = ∠ ( OO 1 ; AB 1 ) = ∠ ( KK 1 ; AB 1 ) . Так как KK 1 || OO 1 , OO 1 ⟂ ( ABC ) , то MK ⟂ AB. Поэтому △ АKМ — прямоугольный. В этом треугольнике АK = , KМ = . Значит, tg ϕ = = , откуда ϕ = arctg .

Ответ: б) , arctg .

Во многих пособиях по геометрии за площадь боковой поверхности цилиндра принимают предел последовательности площадей боковых поверхностей правильных вписанных в цилиндр (или описанных около цилиндра) n- угольных призм при n → + ∞ .

Действительно, S бок. пов. призм = h • P осн. призм , где Р осн. призм — периметр основания призмы, h — длина её высоты. Для правильных вписанных в цилиндр призм h — постоянная величина, равная длине высоты цилиндра, а предел последовательности периметров правильных многоугольников, вписанных в окружность (основание цилиндра), равен длине этой окружности. Таким образом, мы вновь получаем: S бок = 2 π Rh.

17.5. Объём цилиндра

Напомним принятое нами соглашение, основанное на принципе Кавальери.

«Пусть даны два тела и плоскость. Если каждая плоскость, параллельная данной плоскости и пересекающая одно из данных тел, пересекает также и другое, причём площади сечений, образованных при пересечении обоих тел, относятся как m : n, то и объёмы этих тел относятся как m : n ».

Расположим цилиндр, имеющий высоту h и радиус основания R, и прямоугольный параллелепипед с рёбрами h, R, R так, чтобы их основания находились на двух параллельных плоскостях, расстояние между которыми равно h (рис. 162). Каждая плоскость, параллельная данным плоскостям и пересекающая цилиндр, пересекает также прямоугольный параллелепипед, причём площади образованных при пересечении обоих тел сечений относятся как π • R 2 : R 2 = π : 1. Тогда и для объёмов этих тел справедливо: V цил : V парал = π : 1 или V цил : ( R 2 • h ) = π : 1, откуда

V цил = π • R 2 • h.

Если цилиндр высотой h пересечь плоскостью, параллельной его оси, то этот цилиндр разобьётся на два тела (рис. 163). Объёмы этих тел относятся как площади сегментов, образовавшихся в основании цилиндра (докажите это на основании принципа Кавальери). Следовательно, объём каждого из этих тел может быть вычислен по формуле

Любая плоскость, проведённая через середину оси цилиндра, разбивает этот цилиндр на два равновеликих тела (рис. 164), объём V каждого из которых равен половине объёма данного цилиндра, т. е. V = π • R 2 • h.

Попробуйте, исходя из этой формулы, доказать, что в таком случае объём каждой части цилиндра (см. рис. 164) может быть вычислен по формуле:

V= π • R 2 • ( a + b ),

где a и b — длины отрезков, на которые образующая цилиндра делится секущей плоскостью.

📺 Видео

ДЛИНА ОКРУЖНОСТИ и ПЛОЩАДЬ КРУГА 9 класс геометрия АтанасянСкачать

Расчет сегмента окружности по хорде и длине цилиндрической поверхности (трансцендентное уравнение)Скачать

Объем цилиндра.Скачать

КАК НАЙТИ ДЛИНУ ОКРУЖНОСТИ, ЕСЛИ ИЗВЕСТЕН ДИАМЕТР ИЛИ РАДИУС? Примеры | МАТЕМАТИКА 6 классСкачать

Площадь круга. Математика 6 класс.Скачать

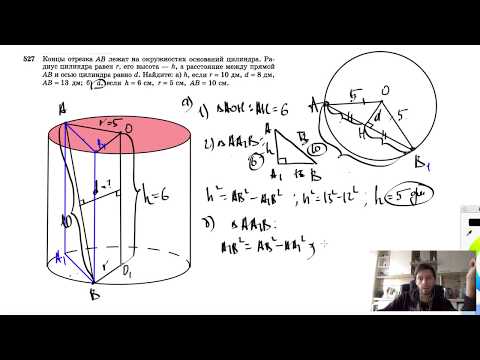
№527. Концы отрезка АВ лежат на окружностях оснований цилиндра. Радиус цилиндра равен г,Скачать

Длина окружности. Площадь круга, 6 классСкачать