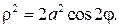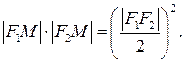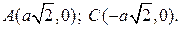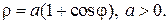Этот онлайн-калькулятор показывает уравнение окружности в стандартной, параметрической и общей формах, по заданному центру и радиусу окружности. Описание и формулы приведены под калькулятором
- Уравнение окружности по заданному центру и радиусу в различных формах
- Центр окружности
- Уравнение окружности
- Общее уравнение окружности
- Стандартное уравнение окружности
- Параметрическое уравнение окружности
- Уравнение окружности в полярных координатах
- Уравнение окружности в параметрическом виде
- 6. Параметрическое задание линий
- Содержание
- Параметрическое представление функции [ править | править код ]
- Параметрическое представление уравнения [ править | править код ]
- Параметрическое уравнение [ править | править код ]
- Примеры [ править | править код ]
- Уравнения некоторых кривых в параметрической форме:
- Формула окружности в параметрическом виде
- 📹 Видео
Уравнение окружности по заданному центру и радиусу в различных формах
Центр окружности
Видео:Видеоурок "Параметрические уравнения прямой"Скачать

Уравнение окружности
Уравнение окружности — это алгебраический способ описания всех точек, лежащих на некоторой окружности. То есть если координаты точки x и y обращают уравнение окружности в равенство — эта точка принадлежит данной окружности. Существуют разные формы записи уравнения окружности:
- общее уравнение окружности
- стандартное уравнение окружности 1
- параметрическое уравнение окружности
- уравнение окружности в полярных координатах
Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Общее уравнение окружности
Общее уравнение окружности с центром и радиусом выглядит так:
,
где
В таком виде довольно сложно судить о свойствах заданной этим уравнением окружности, а именно, о координатах центра и радиусе. Но эту форму достаточно легко привести к стандартной форме (ниже), которая гораздо нагляднее.
Видео:Уравнение окружности (1)Скачать

Стандартное уравнение окружности
Стандартное уравнение окружности с центром и радиусом выглядит так:
Переход от общей формы к стандартной заключается в применении метода выделения полного квадрата. Получив стандартную форму, можно легко узнать координаты центра и радиус. Подробнее можно посмотреть здесь — Метод выделения полного квадрата и здесь — Нахождение центра и радиуса окружности по общему уравнению окружности.
Видео:ГЕОМЕТРИЯ 9 класс: Уравнение окружности и прямойСкачать

Параметрическое уравнение окружности
Параметрическое уравнение окружности с центром и радиусом выглядит так:
Уравнение называется «параметрическим», потому что и x и y зависят от «параметра» тета. Это переменная, которая может принимать любые значения (но конечно это должно быть одно и то же значение в обоих уравнениях). Для параметрического уравнения используется определение синуса и косинуса в прямоугольном треугольнике построенном на радиусе и перпендикуляров от точки на окружности до координатных осей.
Видео:9 класс, 6 урок, Уравнение окружностиСкачать

Уравнение окружности в полярных координатах
Для записи уравнения окружности в полярных координатах требуются полярные координаты центра окружности по отношению к началу координат. Если полярные координаты центра окружности — это , то полярные координаты точки окружности должны удовлетворять следующему уравнению:
,
где a — радиус окружности.
Так, во всяком случае, его называют в англоязычной литературе. Насчет русского термина я не уверен, по-моему эту форму рассматривают просто как еще один способ записи общего уравнения окружности, тем более что переход от общего уравнения к стандартному довольно простой. ↩
Видео:9 класс, 7 урок, Уравнение прямойСкачать

Уравнение окружности в параметрическом виде
Кардиоида
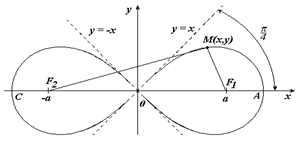
Лемниската Бернулли
Лемниската Бернулли – линия, представляющая геометрическое место точек, расстояние которых от двух данных точек (фокусов) есть постоянная величина, равная квадрату половины межфокусного расстояния.
В полярных координатах
Укажем, что точка М лежит на кривой, если выполнено условие
Вершины кривой находятся в точках
Площадь каждой петли S=a 2 .
В полярных координатах
Вершина кардиоиды находится в точке А(2а,0).
Укажем, что площадь кардиоиды 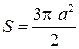
Видео:Написать канонические и параметрические уравнения прямой в пространствеСкачать

6. Параметрическое задание линий
Параметрические уравнения линий задаются в виде зависимости текущих координат x и y от некоторого параметра t. Каждому значению t соответствуют два значения: x и y. При изменении параметра t текущая точка M(x,y) описывает некоторую кривую на плоскости.
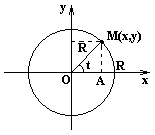 |
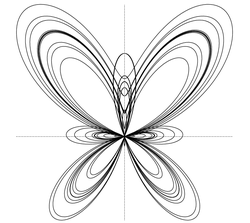
Пусть M(x,y) – текущая точка окружности с центром в начале координат и радиусом R. В качестве параметра t выберем угол, который составляет радиус-вектор точки М с осью ox 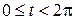
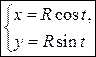
Исключим из параметрических уравнений параметр t. Для этого возведём эти уравнения в квадрат и сложим их:
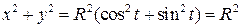
| | | следующая лекция ==> | |
| Четырехлепестковые розы | | | Астроида |
Дата добавления: 2013-12-13 ; Просмотров: 2896 ; Нарушение авторских прав? ;
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Параметрическое представление — используемая в математическом анализе разновидность представления переменных, когда их зависимость выражается через дополнительную величину — параметр.
Видео:Математика без Ху!ни. Уравнение касательной.Скачать

Содержание
Видео:УРАВНЕНИЕ ОКРУЖНОСТИ. ЗАДАНИЕ 18 (С5). АРТУР ШАРИФОВСкачать
Параметрическое представление функции [ править | править код ]
Предположим, что функциональная зависимость y от x не задана непосредственно y = f(x), а через промежуточную величину — t. Тогда формулы
;> 
задают параметрическое представление функции одной переменной.
Если предположить, что обе эти функции φ и ψ имеют производные и для φ существует обратная функция θ, явное представление функции выражается через параметрическое как [1] :
y = ψ ( θ ( x ) ) = f ( x )
и производная функции может быть вычислена как
y ′ ( x ) = d y d x = y t ′ x t ′ = ψ ′ ( t ) ϕ ′ ( t ) >= >>= >
Параметрическое представление даёт такое важное преимущество, что позволяет изучать неявные функции в тех случаях, когда их приведение к явному виду иначе как через параметры затруднительно.
Видео:Уравнение окружностиСкачать

Параметрическое представление уравнения [ править | править код ]
Параметрическое представление для более общего случая: когда переменные связаны уравнением (или системы уравнений, если переменных больше двух).
Видео:начертить окружность. Привести уравнение окружности к стандартному виду. Координаты центра и радиус.Скачать

Параметрическое уравнение [ править | править код ]
Близкое понятие — параметрическое уравнение [2] множества точек, когда координаты точек задаются как функции от некоторого набора свободных параметров. Если параметр один, мы получим параметрическое уравнение кривой.
x = x ( t ) ; y = y ( t ) 

Выражая координаты точек поверхности через два свободных параметра, мы получим параметрическое задание поверхности.
Примеры [ править | править код ]
Уравнение окружности имеет вид:
x 2 + y 2 = r 2 . +y^ =r^ .>
Параметрическое уравнение окружности:
;> 
Параметрическое уравнение правой ветви гиперболы :
t> 
Предположим, что функция $x=phi (t)$ имеет обратную функцию $t= (x)$. Тогда справедливо равенство:
Параметрический способ задания функций широко применяется в механике. Так, если в плоскости некоторая материальная точка находится в движении (время $t$), и законы движения проекций этой точки на оси координат известны:
Уравнения являются параметрическими уравнениями траекторий движущейся точки. Исключая временной параметр, получим уравнение траектории в форме $y = f(x)$.
Определить траекторию и место падения груза, сброшенного с самолета, движущегося горизонтально со скорость $v_0$ на высоте $y_0$.
Допустим, что груз сбрасывается с момент пересечения самолетом оси Oy. Тогда очевидно, что горизонтальное перемещение груза равномерно и имеет постоянную скорость:
А вертикальное перемещение:
Следовательно, расстояние от груза до земли в произвольный момент падения:
Уравнения горизонтального и вертикального перемещения тела являются параметрическими. Для того, чтобы исключить временной параметр $t$, найдем его значение из первого уравнения.
Полученное выражение подставим во второе параметрическое уравнение чтобы найти уравнение траектории:
Попробуй обратиться за помощью к преподавателям
Видео:УРАВНЕНИЕ ОКРУЖНОСТИСкачать

Уравнения некоторых кривых в параметрической форме:
- Окружность
Параметрические кривые окружности:
Рисунок 1. Окружность и ее параметрические кривые
Уравнение гиперболы имеет вид:
Параметрические кривые гиперболы:
Рисунок 2. Гипербола и ее параметрические кривые
Записать уравнение окружности в параметрическом виде.
- Представим уравнение окружности в виде: [x^ +y^ =r^ ] [x^ +y^ =6^ ]
Значит, радиус $r$ равен 6.
Задай вопрос специалистам и получи
ответ уже через 15 минут!
Записать уравнение гиперболы в параметрическом виде.
Так и не нашли ответ
на свой вопрос?
Просто напиши с чем тебе
нужна помощь
Видео:#13. Задача с параметром: уравнение окружности!Скачать

Формула окружности в параметрическом виде
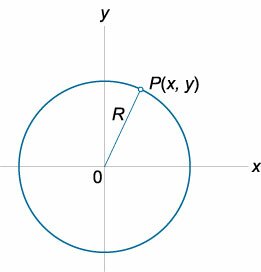
Окружностью называется замкнутая плоская кривая, все точки которой равноудалены от заданной точки (центра окружности). Расстояние от любой точки окружности (Pleft( right)) до ее центра называется радиусом . Центр окружности и сама окружность лежат в одной и той же плоскости. Уравнение окружности радиуса (R) с центром в начале координат ( каноническое уравнение окружности ) имеет вид
( + = ).
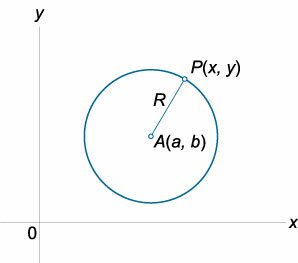
Уравнение окружности радиуса (R) с центром в произвольной точке (Aleft( right)) записывается как
( <left( right)^2> + <left( right)^2> = ).
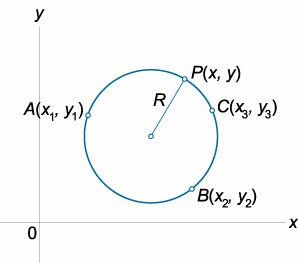
Уравнение окружности, проходящей через три точки , записывается в виде: (left| <begin<*> <+ > & x & y & 1\ & <> & <> & 1\ & <> & <> & 1\ & <> & <> & 1 end> right| = 0.\)
Здесь (Aleft( <,> right)), (Bleft( <,> right)), (Cleft( <,> right)) − три точки, лежащие на окружности.
Уравнение окружности в параметрической форме
( left < beginx &= R cos t \ y &= Rsin t end right., ;;0 le t le 2pi),
где (x), (y) − координаты точек окружности, (R) − радиус окружности, (t) − параметр.
Общее уравнение окружности
(A + A + Dx + Ey + F = 0)
при условии (A ne 0), (D^2 + E^2 > 4AF).
Центр окружности расположен в точке с координатами (left( right)), где
(a = — largefrac<>normalsize,;;b = — largefrac<>normalsize.)
Радиус окружности равен
(R = sqrt <largefrac<<+ — 4AF>><>normalsize> )
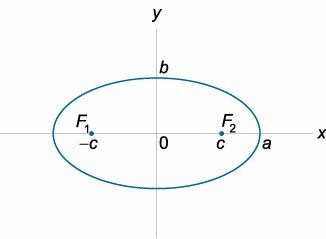
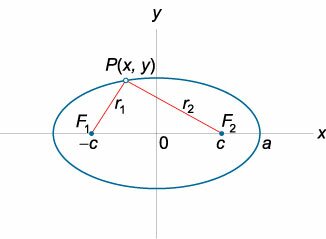
Эллипсом называется плоская кривая, для каждой точки которой сумма расстояний до двух заданных точек ( фокусов эллипса ) постоянна. Расстояние между фокусами называется фокусным расстоянием и обозначается через (2c). Середина отрезка, соединяющего фокусы, называется центром эллипса . У эллипса есть две оси симметрии: первая или фокальная ось, проходящая через фокусы, и перпендикулярная ей вторая ось. Точки пересечения этих осей с эллипсом называются вершинами . Отрезок, соединяющий центр эллипса с вершиной, называется полуосью эллипса . Большая полуось обозначается через (a), малая полуось − через (b). Эллипс, центр которого находится в начале координат, а полуоси лежат на координатных прямых, описывается следующим каноническим уравнением :
(largefrac<<>><<>>normalsize + largefrac<<>><<>>normalsize = 1.)
Сумма расстояний от любой точки эллипса до его фокусов постоянна:
( + = 2a),
где (), () − расстояния от произвольной точки (Pleft( right)) до фокусов () и (), (a) − большая полуось эллипса.
Соотношение между полуосями эллипса и фокусным расстоянием
( = + ),
где (a) − большая полуось эллипса, (b) − малая полуось, (c) − половина фокусного расстояния.
Уравнение эллипса в параметрической форме
( left < beginx &= acos t \ y &= bsin t end right., ;;0 le t le 2pi),
где (a), (b) − полуоси эллипса, (t) − параметр.
Общее уравнение эллипса
(A + Bxy + C + Dx + Ey + F = 0),
где ( — 4AC Общее уравнение эллипса, полуоси которого параллельны осям координат
(A + C + Dx + Ey + F = 0),
где (AC > 0).
Периметр эллипса
(L = 4aEleft( e right)),
где (a) − большая полуось эллипса, (e) − эксцентриситет, (E) − полный эллиптический интеграл второго рода.
Приближенные формулы для периметра эллипса
(L approx pi left[ <largefracnormalsizeleft( right) — sqrt > right],;;L approx pi sqrt <2left( <+ > right)>,)
где (a), (b) − полуоси эллипса.
Площадь эллипса
(S = pi ab)
📹 Видео
Уравнение окружности и формула расстояния между точками на плоскостиСкачать

Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

Видеоурок "Канонические уравнения прямой"Скачать

Уравнение окружности | Геометрия 7-9 класс #90| ИнфоурокСкачать

14. Что такое параметрически заданная функция, производная параметрически заданной функции.Скачать

ПРОСТОЙ СЕКРЕТ ДЛЯ НАЧИНАЮЩИХ! Реши алгебру за 12 минут — Уравнение ОкружностиСкачать