Окружность — это геометрическое место точек плоскости, равноудаленных от некоторой заданной точки (центра окружности). Расстояние между любой точкой окружности и ее центром называется радиусом окружности (радиус обозначают буквой R).
Значит, окружность — это линия на плоскости, каждая точка которой расположена на одинаковом расстоянии от центра окружности.
Кругом называется часть плоскости, ограниченная окружностью и включающая ее центр.
Отрезок, соединяющий две точки окружности, называется хордой. Хорда, проходящая через центр окружности, представляет собой диаметр. Диаметр окружности равен ее удвоенному радиусу: D = 2R.
Точка пересечения двух хорд делит каждую хорду на отрезки, произведение которых одинаково: a1a2 = b1b2
Касательная к окружности всегда перпендикулярна радиусу, проведенному в точку касания.
Отрезки касательных к окружности, проведенные из одной точки, равны: AB = AC, центр окружности лежит на биссектрисе угла BAC.
Квадрат касательной равен произведению секущей на ее внешнюю часть
Центральный угол — это угол, вершина которого совпадает с центром окружности.
Дугой называется часть окружности, заключенная между двумя точками.
Мерой дуги (в градусах или радианах) является центральный угол, опирающийся на данную дугу.
Вписанный угол это угол, вершина которого лежит на окружности, а cтороны угла пересекают ее.
Вписанный угол равен половине центрального, если оба угла опираются на одну и ту же дугу окружности.
Внутренние углы, опирающиеся на одну и ту же дугу, равны.
Сектором круга называется геометрическая фигура, ограниченная двумя радиусами и дугой, на которую опираются данные радиусы.
Периметр сектора: P = s + 2R.
Площадь сектора: S = Rs/2 = ПR 2 а/360°.
Сегментом круга называется геометрическая фигура, ограниченная хордой и стягиваемой ею дугой.
- Найти наибольшее расстояние от точки до окружности
- Найти наибольшее расстояние от точки до окружности
- Наименьшее расстояние между точкой и окружностью
- Вычислительная геометрия, или как я стал заниматься олимпиадным программированием. Часть 2
- Вступление
- Наименьшее расстояние между точкой и окружностью
- 📸 Видео
Видео:Как искать точки на тригонометрической окружности.Скачать

Найти наибольшее расстояние от точки до окружности
Видео:Расстояние от точки до плоскости / Вывод формулыСкачать

Найти наибольшее расстояние от точки до окружности
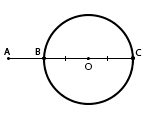
56. Наибольшее и наименьшее расстояния от точки, лежащей вне окружности, до окружности равны 6 и 2. Найдите длину окружности.
АС — наибольшее расстояние от точки А до окружности и равно 6.
АВ — наименьшее расстояние от точки А до окружности и равно 2.
О — центр окружности.
ВО и СО — радиусы окружности.
Следовательно, радиус окружности составляет 4 : 2 = 2 (ВО = СО = R = 2).
Зная радиус, можно найти длину окружности по формуле:
В данном случае длина окружности:
Если вы заметили орфографическую ошибку, пожалуйста, выделите ее мышью и нажмите Ctrl+Enter
Видео:"Парадоксальное" среднее расстояние между точками на окружностиСкачать

Наименьшее расстояние между точкой и окружностью
Данный круг с данным радиусом имеет свой центр в определенной позиции в координатной плоскости. В координатной плоскости задается другая точка. Задача — найти кратчайшее расстояние между точкой и окружностью.
Примеры:
Подход :
который равен (др)
d = √ ((x2-x1) ^ 2 — (y2-y1) ^ 2)

Ниже приведена реализация вышеуказанного подхода:
// C ++ программа для поиска
// Наименьшее расстояние
// между точкой и
// круг
#include
using namespace std;
// Функция для поиска кратчайшего расстояния
void dist( double x1, double y1, double x2, double y2, double r)
cout «The shortest distance «
«between a point and a circle is «
sqrt (( pow ((x2 — x1), 2))
double x1 = 4, y1 = 6,
x2 = 35, y2 = 42, r = 5;
dist(x1, y1, x2, y2, r);
// Java-программа для поиска
// Наименьшее расстояние
// между точкой и
// круг
// Функция для поиска кратчайшего расстояния
static void dist( double x1, double y1, double x2,
double y2, double r)
System.out.println( «The shortest distance «
+ «between a point and a circle is «
+ (Math.sqrt((Math.pow((x2 — x1), 2 ))
+ (Math.pow((y2 — y1), 2 )))
public static void main(String[] args)
double x1 = 4 , y1 = 6 ,
x2 = 35 , y2 = 42 , r = 5 ;
dist(x1, y1, x2, y2, r);
/ * Этот код предоставлен PrinciRaj1992 * /
# Python программа для поиска
# Наименьшее расстояние
# между точкой и
# круг
# Функция поиска кратчайшего расстояния
def dist(x1, y1, x2, y2, r):
print ( «The shortest distance between a point and a circle is «
,((((x2 — x1) * * 2 ) + ((y2 — y1) * * 2 )) * * ( 1 / 2 )) — r);
dist(x1, y1, x2, y2, r);
# Этот код предоставлен 29AjayKumar
// C # программа для поиска кратчайшего расстояния
// между точкой и окружностью
// Функция для поиска кратчайшего расстояния
static void dist( double x1, double y1, double x2,
double y2, double r)
Console.WriteLine( «The shortest distance «
+ «between a point and a circle is «
+ (Math.Sqrt((Math.Pow((x2 — x1), 2))
+ (Math.Pow((y2 — y1), 2)))
public static void Main(String[] args)
double x1 = 4, y1 = 6,
x2 = 35, y2 = 42, r = 5;
dist(x1, y1, x2, y2, r);
/ * Этот код предоставлен PrinciRaj1992 * /
// PHP программа для поиска
// Наименьшее расстояние
// между точкой и
// круг
// Функция для поиска кратчайшего расстояния
function dist( $x1 , $y1 , $x2 , $y2 , $r )
echo «The shortest distance between a point and a circle is «
Видео:Определение кратчайшей расстояние от точки до плоскости способом замены плоскостей проекцииСкачать

Вычислительная геометрия, или как я стал заниматься олимпиадным программированием. Часть 2
Вступление
Это вторая часть моей статьи посвящена вычислительной геометрии. Думаю, эта статья будет интереснее предыдущей, поскольку задачки будут чуть сложнее.
Начнем с взаимного расположения точки относительно прямой, луча и отрезка.
Задача №1
Определить взаимное расположении точки и прямой: лежит выше прямой, на прямой, под прямой.
Решение
Понятно, что если прямая задана своим уравнением ax + by + c = 0, то тут и решать нечего. Достаточно подставить координаты точки в уравнение прямой и проверить чему оно равно. Если больше нуля, то точка находится в верхней полуплоскости, если равна нулю, то точка находится на прямой и если меньше нуля, то точка находится в нижней полуплоскости. Интереснее случай, когда прямая задана, задана координатами двух точек назовем их P1(x1, y1), P2(x2, y2). В этом случае можно спокойно найти коэффициенты a, b и c и применить предыдущее рассуждение. Но надо сначала подумать, оно нам надо? Конечно, нет! Как я говорил косое произведения — это просто жемчужина вычислительной геометрии. Давайте применим его. Известно, что косое произведение двух векторов положительно, если поворот от первого вектора ко второму идет против часовой стрелки, равно нулю, если векторы коллинеарны и отрицательно, если поворот идет по часовой стрелки. Поэтому нам достаточно посчитать косое произведение векторов P1P2 и P1M и по его знаку сделать вывод.
Задача №2
Определить принадлежит ли точка лучу.
Решение
Давайте вспомним, что такое луч: луч — это прямая, ограниченная точкой с одной стороны, а с другой стороны бесконечная. То есть луч задается некоторой начальной точкой и любой точкой лежащей на нем. Пусть точка P1(x1, y1) — начало луча, а P2(x2, y2) — любая точка принадлежащая лучу. Понятно, что если точка принадлежит лучу, то она принадлежит и прямой проходящей через эти точки, но не наоборот. Поэтому принадлежность прямой является необходимым, но не достаточным условием для принадлежности лучу. Поэтому от проверки косового произведения нам никуда не деться. Для достаточного условия нужно вычислить еще и скалярное произведение тех же векторов. Если оно меньше нуля, то точка не принадлежит лучу, если же оно не отрицательно, то точка лежит на луче. Почему так? Давайте посмотрим на рисунок.
Итак, для того чтобы точка M(x, y) лежала на луче с начальной точкой P1(x1, y1), где P2(x2, y2) лежит на луче необходимо и достаточно выполнения двух условий:
1. [P1P2, P1M] = 0 – косое произведение (точка лежит на прямой)
2. (P1P2, P1M) ≥ 0 – скалярное произведение (точка лежит на луче)
Задача №3
Определить принадлежит ли точка отрезку.
Решение
Пусть точки P1(x1, y1), P2(x2, y2) концы заданного отрезка. Опять-таки необходимым условием принадлежности точки отрезку является ее принадлежность прямой проходящей через P1, P2. Далее нам нужно определить лежит ли точка между точками P1 и P2, для этого нам на помощь приходит скалярное произведение векторов только на этот раз других: (MP1, MP2). Если оно меньше либо равно нуля, то точка лежит на отрезке, иначе вне отрезка. Почему так? Посмотрим на рисунок.
Итак, для того чтобы точка M(x, y) лежала на отрезке с концами P1(x1, y1), P2(x2, y2) необходимо и достаточно выполнения условий:
1. [P1P2, P1M] = 0 – косое произведение (точка лежит на прямой)
2. (MP1,MP2) ≤ 0 – скалярное произведение (точка лежит между P1 и P2)
Задача №4
Взаимное расположение двух точек относительно прямой.
Решение
В этой задаче необходимо определить по одну или по разные стороны относительно прямой находятся две точки.
Если точки находятся по разные стороны относительно прямой, то косые произведения имеют разные знаки, а значит их произведение отрицательно. Если же точки лежат по одну сторону относительно прямой, то знаки косых произведений совпадают, значит, их произведение положительно.
Итак:
1. [P1P2, P1M1] * [P1P2, P1M2] 0 – точки лежат по одну сторону.
3. [P1P2, P1M1] * [P1P2, P1M2] = 0 – одна (или две) из точек лежит на прямой.
Кстати, задача об определении наличия точки пересечения у прямой и отрезка решается точно также. Точнее, это и есть эта же задача: отрезок и прямая пересекаются, когда концы отрезка находятся по разные стороны относительно прямой или когда концы отрезка лежат на прямой, то есть необходимо потребовать [P1P2, P1M1] * [P1P2, P1M2] ≤ 0.
Задача №5
Определить пересекаются ли две прямые.
Решение
Будем считать, что прямые не совпадают. Понятно, что прямые не пересекаются, только если они параллельны. Поэтому, найдя условие параллельности, мы можем, определить пересекаются ли прямые.
Допустим прямые заданы своими уравнениями a1x + b1y + c1 = 0 и a2x + b2y + c2 = 0. Тогда условие параллельности прямых заключается в том, что a1b2 — a2b1 = 0.
Если же прямые заданы точками P1(x1, y1), P2(x2, y2), M1(x3, y3), M2(x4, y4), то условие их параллельности заключается в проверки косого произведения векторов P1P2 и M1M2: если оно равно нулю, то прямые параллельны.
В общем, то когда прямые заданы своими уравнениями мы тоже проверяем косое произведение векторов (-b1, a1), (-b2, a2) которые называются направляющими векторами.
Задача №6
Определить пересекаются ли два отрезка.
Решение
Вот эта задача мне, действительно, нравится. Отрезки пересекаются тогда, когда, концы каждого отрезка лежат по разные стороны от другого отрезка. Посмотрим на рисунок:
Итак, нам нужно проверить, чтобы концы каждого из отрезков лежали по разные стороны относительного концов другого отрезка. Пользуемся косым произведением векторов. Посмотрите на первый рисунок: [P1P2, P1M2] > 0, [P1P2, P1M1] [P1P2, P1M2] * [P1P2, P1M1] 2 + b 2 ).
Задача №8
Расстояние от точки до луча.
Решение
Эта задача отличается от предыдущей тем, что в этом случае может получиться, так что перпендикуляр из точки не падает на луч, а падает на его продолжение.
В случае, когда перпендикуляр не падает на луч необходимо найти расстояние от точки до начала луча – это и будет ответом на задачу.
Как же определить падает ли перпендикуляр на луч или нет? Если перпендикуляр не падает на луч, то угол MP1P2 – тупой иначе острый (прямой). Поэтому по знаку скалярного произведения векторов мы можем определить попадает ли перпендикуляр на луч или нет:
1. (P1M, P1P2) 2 .
Теперь рассмотрим случай, когда центр второго круга O2 находится между точками O1 и C. В этом случае получим отрицательное значение величины d2. Использование отрицательного значения d2 приводит к отрицательному значению α. В этом случае необходимо для правильного ответа прибавить к α 2π.
Заключение
Ну вот и все. Мы рассмотрели не все, но наиболее часто встречаемые задачи вычислительной геометрии касающиеся взаимного расположения объектов.
Видео:7. Расстояние от точки до плоскости (вывод формулы примеры)Скачать

Наименьшее расстояние между точкой и окружностью
Данный круг с данным радиусом имеет свой центр в определенной позиции в координатной плоскости. В координатной плоскости задается другая точка. Задача — найти кратчайшее расстояние между точкой и окружностью.
Примеры:
Подход :
который равен (др)
d = √ ((x2-x1) ^ 2 — (y2-y1) ^ 2)

Ниже приведена реализация вышеуказанного подхода:
// C ++ программа для поиска
// Наименьшее расстояние
// между точкой и
// круг
#include
using namespace std;
// Функция для поиска кратчайшего расстояния
void dist( double x1, double y1, double x2, double y2, double r)
cout «The shortest distance «
«between a point and a circle is «
sqrt (( pow ((x2 — x1), 2))
double x1 = 4, y1 = 6,
x2 = 35, y2 = 42, r = 5;
dist(x1, y1, x2, y2, r);
// Java-программа для поиска
// Наименьшее расстояние
// между точкой и
// круг
// Функция для поиска кратчайшего расстояния
static void dist( double x1, double y1, double x2,
double y2, double r)
System.out.println( «The shortest distance «
+ «between a point and a circle is «
+ (Math.sqrt((Math.pow((x2 — x1), 2 ))
+ (Math.pow((y2 — y1), 2 )))
public static void main(String[] args)
double x1 = 4 , y1 = 6 ,
x2 = 35 , y2 = 42 , r = 5 ;
dist(x1, y1, x2, y2, r);
/ * Этот код предоставлен PrinciRaj1992 * /
# Python программа для поиска
# Наименьшее расстояние
# между точкой и
# круг
# Функция поиска кратчайшего расстояния
def dist(x1, y1, x2, y2, r):
print ( «The shortest distance between a point and a circle is «
,((((x2 — x1) * * 2 ) + ((y2 — y1) * * 2 )) * * ( 1 / 2 )) — r);
dist(x1, y1, x2, y2, r);
# Этот код предоставлен 29AjayKumar
// C # программа для поиска кратчайшего расстояния
// между точкой и окружностью
// Функция для поиска кратчайшего расстояния
static void dist( double x1, double y1, double x2,
double y2, double r)
Console.WriteLine( «The shortest distance «
+ «between a point and a circle is «
+ (Math.Sqrt((Math.Pow((x2 — x1), 2))
+ (Math.Pow((y2 — y1), 2)))
public static void Main(String[] args)
double x1 = 4, y1 = 6,
x2 = 35, y2 = 42, r = 5;
dist(x1, y1, x2, y2, r);
/ * Этот код предоставлен PrinciRaj1992 * /
// PHP программа для поиска
// Наименьшее расстояние
// между точкой и
// круг
// Функция для поиска кратчайшего расстояния
function dist( $x1 , $y1 , $x2 , $y2 , $r )
echo «The shortest distance between a point and a circle is «
📸 Видео
10 класс, 19 урок, Расстояние от точки до плоскостиСкачать

Определение кратчайшей расстоянии от точки до плоскостиСкачать

Расстояние. Математика. 6 классСкачать

7 класс, 38 урок, Расстояние от точки до прямой. Расстояние между параллельными прямымиСкачать

№632. Расстояние от точки А до центра окружности меньше радиуса окружности. Докажите, что любаяСкачать

Расстояние от точки до прямойСкачать

Расстояние от точки до плоскости. 11 класс.Скачать
18. Расстояние от точки до прямой в пространствеСкачать

10 класс, 11 урок, Числовая окружностьСкачать

Геометрия 7 класс (Урок№26 - Расстояние от точки до прямой. Расстояние между параллельными прямыми.)Скачать

Расстояние от точки до прямой (метод координат)Скачать

Видеоурок "Расстояние от точки до прямой"Скачать

Уравнение окружности и формула расстояния между точками на плоскостиСкачать

Расстояние от точки до прямой | Вывод формулы через Подобие и ПифагораСкачать

расстояние от точки до плоскостиСкачать