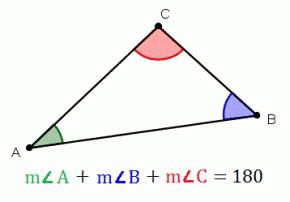
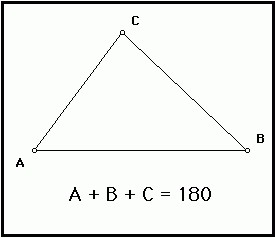
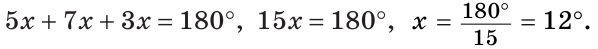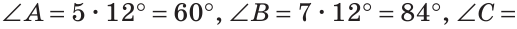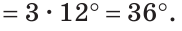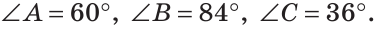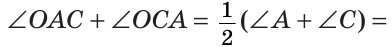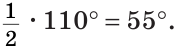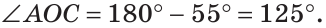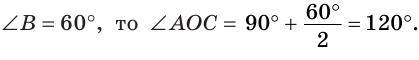Треугольник представляет собой многоугольник, имеющий три стороны (три угла). Чаще всего стороны обозначают маленькими буквами, соответствующими заглавным буквам, которыми обозначают противоположные вершины. В данной статье мы ознакомимся с видами этих геометрических фигур, теоремой, которая определяет, чему равняется сумма углов треугольника.
- Виды по величине углов
- Свойства
- Теорема о сумме углов треугольника
- Следствие
- Свойство внешних углов
- Прямоугольный треугольник
- Сумма углов равнобедренного треугольника
- Равносторонний треугольник
- Тупоугольный треугольник
- Методическая разработка на тему»Сумма углов треугольника»
- Описание презентации по отдельным слайдам:
- Сумма углов треугольника — определение и вычисление с доказательствами и примерами решения
- 📹 Видео
Видео:Геометрия 7 класс (Урок№23 - Сумма углов треугольника.)Скачать

Виды по величине углов
Различают следующие виды многоугольника с тремя вершинами:
- остроугольный, у которого все углы острые;
- прямоугольный, имеющий один прямой угол, при этом стороны, его образующие, называют катетами, а сторона, которая размещена противоположно прямому углу, именуется гипотенузой;
- тупоугольный, когда один угол тупой;
- равнобедренный, у которого две стороны равные, и называются они боковыми, а третья – основанием треугольника;
- равносторонний, имеющий все три равные стороны.
Видео:Геометрия за 6 минут — Сумма углов треугольника и Внешний УголСкачать

Свойства
Выделяют основные свойства, которые характерны для каждого вида треугольника:
- напротив большей стороны всегда располагается больший угол, и наоборот;
- напротив равных по величине сторон находятся равные углы, и наоборот;
- у любого треугольника есть два острых угла;
- внешний угол больше по сравнению с любым внутренним углом, не смежным с ним;
- сумма каких-либо двух углов всегда меньше 180 градусов;
- внешний угол равняется сумме остальных двух углов, которые не межуют с ним.
Видео:Сумма углов треугольника. Геометрия 7 класс | МатематикаСкачать

Теорема о сумме углов треугольника
Теорема утверждает, что если сложить все углы данной геометрической фигуры, которая расположена на евклидовой плоскости, то их сумма будет составлять 180 градусов. Попробуем доказать данную теорему.
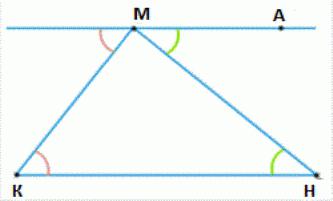
Пускай у нас есть произвольный треугольник с вершинами КМН.
Видео:Сумма углов треугольникаСкачать

Следствие
Из выше доказанной теоремы вытекает следующее следствие: любой треугольник имеет два острых угла. Чтобы это доказать, допустим, что данная геометрическая фигура имеет всего один острый угол. Также можно предположить, что ни один из углов не является острым. В этом случае должно быть как минимум два угла, величина которых равна или больше 90 градусов. Но тогда сумма углов будет больше, чем 180 градусов. А такого быть не может, поскольку согласно теореме сумма углов треугольника равна 180° — не больше и не меньше. Вот это и нужно было доказать.
Видео:Соотношения между сторонами и углами треугольника. 7 класс.Скачать

Свойство внешних углов
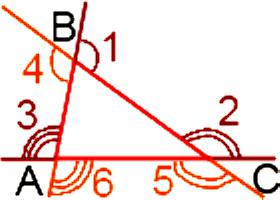
Чему равна сумма углов треугольника, которые являются внешними? Ответ на этот вопрос можно получить, применив один из двух способов. Первый заключается в том, что необходимо найти сумму углов, которые взяты по одному при каждой вершине, то есть трех углов. Второй подразумевает, что нужно найти сумму всех шести углов при вершинах. Для начала разберемся с первым вариантом. Итак, треугольник содержит шесть внешних углов – при каждой вершине по два.
Кроме этого, известно, что внешний угол у треугольника равняется сумме двух внутренних, которые не межуются с ним. Следовательно,
∟1 = ∟А + ∟С, ∟2 = ∟А + ∟В, ∟3 = ∟В + ∟С.
Из этого получается, что сумма внешних углов, которые взяты по одному возле каждой вершины, будет равна:
∟1 + ∟2 + ∟3 = ∟А + ∟С + ∟А + ∟В + ∟В + ∟С = 2 х (∟А + ∟В + ∟С).
С учетом того, что сумма углов равняется 180 градусам, можно утверждать, что ∟А + ∟В + ∟С = 180°. А это значит, что ∟1 + ∟2 + ∟3 = 2 х 180° = 360°. Если же применяется второй вариант, то сумма шести углов будет, соответственно, большей в два раза. То есть сумма внешних углов треугольника будет составлять:
∟1 + ∟2 + ∟3 + ∟4 + ∟5 + ∟6 = 2 х (∟1 + ∟2 + ∟2) = 720°.
Видео:7 класс, 31 урок, Теорема о сумме углов треугольникаСкачать

Прямоугольный треугольник
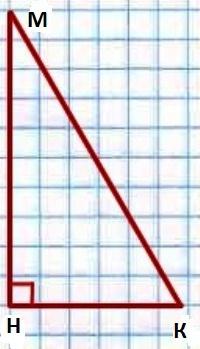
Чему равняется сумма углов прямоугольного треугольника, являющихся острыми? Ответ на этот вопрос, опять же, вытекает из теоремы, которая утверждает, что углы в треугольнике в сумме составляют 180 градусов. А звучит наше утверждение (свойство) так: в прямоугольном треугольнике острые углы в сумме дают 90 градусов. Докажем его правдивость.
Итак, согласно теореме о сумме углов ∟К + ∟М + ∟Н = 180°. В нашем условии сказано, что ∟Н = 90°. Вот и получается, ∟К + ∟М + 90° = 180°. То есть ∟К + ∟М = 180° — 90° = 90°. Именно это нам и следовало доказать.
В дополнение к вышеописанным свойствам прямоугольного треугольника, можно добавить и такие:
- углы, которые лежат против катетов, являются острыми;
- гипотенуза треугольна больше любого из катетов;
- сумма катетов больше гипотенузы;
- катет треугольника, который лежит напротив угла 30 градусов, в два раза меньше гипотенузы, то есть равняется ее половине.
Как еще одно свойство данной геометрической фигуры можно выделить теорему Пифагора. Она утверждает, что в треугольнике с углом 90 градусов (прямоугольном) сумма квадратов катетов равняется квадрату гипотенузы.
Видео:СУММА УГЛОВ ТРЕУГОЛЬНИКА. §16 геометрия 7 классСкачать

Сумма углов равнобедренного треугольника
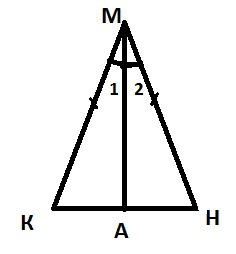
Ранее мы говорили, что равнобедренным называют многоугольник с тремя вершинами, содержащий две равные стороны. Известно такое свойство данной геометрической фигуры: углы при его основании равны. Докажем это.
Возьмем треугольник КМН, который является равнобедренным, КН – его основание.
Но нас интересует, какова сумма углов треугольника (равнобедренного). Поскольку в этом отношении у него нет своих особенностей, будем отталкиваться от теоремы, рассмотренной ранее. То есть мы можем утверждать, что ∟К + ∟М + ∟Н = 180°, или 2 х ∟К + ∟М = 180° (поскольку ∟К = ∟Н). Данное свойство доказывать не будем, поскольку сама теорема о сумме углов треугольника была доказана ранее.
Кроме рассмотренных свойств об углах треугольника, имеют место и такие немаловажные утверждения:
- в равнобедренном треугольнике высота, которая была опущена на основание, является одновременно медианой, биссектрисой угла, который находится между равными сторонами, а также осью симметрии его основания;
- медианы (биссектрисы, высоты), которые проведены к боковым сторонам такой геометрической фигуры, равны.
Видео:Геометрия 7 класс. Сумма углов треугольникаСкачать

Равносторонний треугольник
Его еще называют правильным, это тот треугольник, у которого равны все стороны. А поэтому равны также и углы. Каждый из них составляет 60 градусов. Докажем это свойство.
Допустим, что у нас есть треугольник КМН. Нам известно, что КМ = НМ = КН. А это значит, что согласно свойству углов, расположенных при основании в равнобедренном треугольнике, ∟К = ∟М = ∟Н. Поскольку согласно теореме сумма углов треугольника ∟К + ∟М + ∟Н = 180°, то 3 х ∟К = 180° или ∟К = 60°, ∟М = 60°, ∟Н = 60°. Таким образом, утверждение доказано.
Существуют еще такие свойства, характерные для равностороннего треугольника:
- медиана, биссектриса, высота в такой геометрической фигуре совпадают, а их длина вычисляется как (а х √3) : 2;
- если описать вокруг данного многоугольника окружность, то ее радиус будет равен (а х √3) : 3;
- если вписать в равносторонний треугольник окружность, то ее радиус будет составлять (а х √3) : 6;
- площадь этой геометрической фигуры вычисляется по формуле: (а2 х √3) : 4.
Видео:Сумма углов треугольника. Доказательство теоремы о сумме углов треугольника. Геометрия 7 класс.Скачать

Тупоугольный треугольник
Согласно определению тупоугольного треугольника, один из его углов находится в промежутке от 90 до 180 градусов. Но учитывая то, что два остальных угла данной геометрической фигуры острые, можно сделать вывод, что они не превышают 90 градусов. Следовательно, теорема о сумме углов треугольника работает при расчете суммы углов в тупоугольном треугольнике. Получается, мы смело можем утверждать, опираясь на вышеупомянутую теорему, что сумма углов тупоугольного треугольника равна 180 градусам. Опять-таки, данная теорема не нуждается в повторном доказательстве.
Видео:СУММА УГЛОВ ТРЕУГОЛЬНИКА доказательство 7 класс геометрия АтанасянСкачать

Методическая разработка на тему»Сумма углов треугольника»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
«Актуальность создания школьных служб примирения/медиации в образовательных организациях»
Свидетельство и скидка на обучение каждому участнику
Описание презентации по отдельным слайдам:
Краевое государственное бюджетное профессиональное образовательное учреждение «Хабаровский техникум техносферной безопасности и промышленных технологий», Хабаровский край , г. Хабаровск Тема: «Сумма углов треугольника» Михайлова Мария Борисовна, преподаватель математики 1800
Аннотация В работе рассмотрена тема: «Сумма углов треугольника на евклидовой плоскости». Интерес к этой теме поддерживается тем, что треугольники часто встречаются в различных явлениях природы, физике, картографии, геодезии, строительстве и в человеческой деятельности, а теорема о сумме углов треугольника используется в геодезии, строительстве и др. областях.
Цели работы: расширение и углубление знаний о сумме углов треугольника; знакомство постулатами Евклида; доказательство теоремы о сумме углов треугольника; знакомство с неевклидовыми геометриями – геометрией Лобачевского и сферической геометрией.
Из истории открытия Свойство суммы углов треугольника было установлено эмпирически, то есть опытным путем, еще в Древнем Египте. Однако дошедшие до нас сведения об его доказательствах относятся к более позднему времени. Доказательство, изложенное в современных учебниках, содержится в комментарии Прокла к «Началам» Евклида. Прокл утверждает, что согласно Евдему Родосскому это доказательство было открыто еще пифагорейцами (V в. до н. э.) Прокл пишет: «Пифагор впервые разработал принципы геометрии». Пифагорейцы содействовали формированию геометрии как науки, основанной на аксиомах и доказательствах. Евкли́д (ок. 300 г. до н. э.) — древнегреческий математик, автор первого из дошедших до нас теоретических трактатов по математике. Известен как «Отец Геометрии»
Сам же Прокл, комментируя первую книгу «Начала» Евклида, утверждал, что согласно Евдему Родосскому (IV в. до н.э.) сумма углов треугольника равна развёрнутому углу. Он в своих комментариях приводит доказательство, основанное на чертеже:
А в книге «Начала» Евклида излагается доказательство теоремы о сумме углов треугольника, которое легко понять с помощью чертежа:
Папирус из Оксиринха Следует отметить, что как доказательство Прокла, так и доказательство Евклида основываются на том, что при пересечении двух параллельных прямых третьей внутренние накрест лежащие, а также и соответственные углы равны. Это предложение в свою очередь доказывается при помощи аксиомы параллельности Евклида или пятого постулата Евклида. Итак, теорема о том, что сумма углов треугольника равна 2d, верна, если верна аксиома параллельности Евклида, которая принята в системе аксиом Евклида без доказательства. Наиболее интересен в аксиоматике Евклида последний, знаменитый пятый постулат. Среди других, интуитивно очевидных постулатов, он нарочито чужероден, его громоздкая формулировка закономерно вызывает некоторое чувство протеста и желание отыскать для него доказательство. Такие доказательства уже в древности пытались построить Птолемей и Прокл; а в Новое время из этих попыток развилась неевклидова геометрия – геометрия Лобачевского и сферическая геометрия. Папирус из Оксиринха содержащий небольшой фрагмент «Начал» Евклида
Аксиома параллельности Евклида, или пятый постулат — одна из аксиом, лежащих в основании классической планиметрии. Впервые приведена в «Началах» Евклида. И если прямая, падающая на две прямые, образует внутренние и по одну сторону углы, меньшие двух прямых, то продолженные неограниченно эти прямые встретятся с той стороны, где углы меньше двух прямых.
Постулаты Евклида На современном языке текст Евклида можно переформулировать так: Если сумма внутренних углов с общей стороной, образованных двумя прямыми при пересечении их третьей, с одной из сторон от секущей меньше 180°, то эти прямые пересекаются, и притом по ту же сторону от секущей.
Вообще у V постулата имеется огромное количество эквивалентных формулировок, многие из которых кажутся довольно очевидными. Вот некоторые из них Существует прямоугольник (хотя бы один), то есть четырёхугольник, у которого все углы прямые. Сумма углов одинакова у всех треугольников. Существует треугольник, сумма углов которого равна двум прямым. Вариант: существует, как минимум, одна пара неравновеликих треугольников с одинаковой суммой углов. Существует треугольник (по меньшей мере один), сумма углов которого равна двум прямым. Вариант: существует N-угольник, сумма углов которого равна 1800*(N-2). Эквивалентность их означает, что все они могут быть доказаны, если принять V постулат, и наоборот, заменив V постулат на любое из этих утверждений, мы сможем доказать исходный V постулат как теорему
Теорема о сумме углов треугольника — классическая теорема евклидовой геометрии. Утверждает, что сумма углов треугольника на евклидовой плоскости равна 180°. 1800
Доказательство Пусть ABC — произвольный треугольник. Проведем через вершину B прямую, параллельную прямой AC (такая прямая называется прямой Евклида). Отметим на ней точку D так, чтобы точки A и D лежали по разные стороны от прямой BC. Углы DBC и ACB равны как внутренние накрест лежащие, образованные секущей BC с параллельными прямыми AC и BD. Поэтому сумма углов треугольника при вершинах B и С равна углу ABD. Сумма всех трех углов треугольника равна сумме углов ABD и BAC. Так как эти углы внутренние односторонние для параллельных AC и BD при секущей AB, то их сумма равна 180°. Теорема доказана.
Следствия Из теоремы следует, что у любого треугольника два угла острые. Действительно, применяя доказательство от противного, допустим, что у треугольника только один острый угол или вообще нет острых углов. Тогда у этого треугольника есть, по крайней мере, два угла, каждый из которых не меньше 90°. Сумма этих углов не меньше 180°. А это невозможно, так как сумма всех углов треугольника равна 180°. Что и требовалось доказать.
Сумма углов треугольника в неевклидовой геометрии – геометрии Лобачевского и сферической геометрии
Евклидова геометрия (А) отнюдь не единственная. Возможно, что реальное пространство обладает иной геометрией. В геометрии Лобачевского, как в геометрии на воронкообразной поверхности (Б), сумма углов треугольника всегда меньше 180°. В геометрии Римана, как в геометрии на поверхности сферы (В), сумма углов треугольника всегда больше 180°. Распространенная на трехмерный случай, эта геометрия дает геометрию искривленного пространства. А В А В Б Разность суммы углов треугольника и 180° называется дефектом. Дефект пропорционален площади треугольника, таким образом, у бесконечно малых треугольников на сфере или плоскости Лобачевского сумма углов будет мало отличаться от 180°.
На сфере сумма углов треугольника всегда превышает 180°, разница называется сферическим избытком и пропорциональна площади треугольника. Сферический треугольник — геометрическая фигура на поверхности сферы, образованная пересечением трёх больших кругов. Три больших круга на поверхности сферы, не пересекающихся в одной точке, образуют восемь сферических треугольников.
Сферический треугольник Сумма углов сферического треугольника всегда меньше и больше . Величина называется сферическим избытком или сферическим эксцессом. Если от двух углов сферического треугольника отнимем третий, получим угол, меньший . В отличие от плоского треугольника, у сферического треугольника может быть два тупых угла или два прямых угла.
У сферического треугольника может быть два прямых угла Углы сферического треугольника – это углы между касательными к его сторонам, проведенными в его вершинах. Как и углы обычного треугольника, они меняются от 0 до 180°. В отличие от плоского треугольника, у сферического сумма углов не равна 180°, а больше: в этом нетрудно убедиться, рассмотрев, например, треугольник, образованный дугами двух меридианов и экватора на глобусе: хотя меридианы сходятся в полюсе, оба они перпендикулярны экватору, а значит, у этого треугольника два прямых угла!
В плоскости Лобачевского сумма углов треугольника всегда меньше 180°. Разность также пропорциональна площади треугольника. Сумма углов всякого треугольника меньше и может быть сколь угодно близкой к нулю. Это непосредственно видно на модели Пуанкаре. Разность где — углы треугольника, пропорциональна его площади: Здесь q — некоторая постоянная, связанная с кривизной пространства Лобачевского. Она может служить абсолютной единицей длины аналогично тому, как в сферической геометрии особое положение занимает радиус сферы. Модель плоскости Лобачевского – модель Пуанкаре
о применении свойств треугольника — суммы углов треугольника в древности Греческий мудрец Фалес из Милета за шесть веков до нашей эры определил в Египте высоту пирамиды. Он воспользовался тенью. Как говорит придание, Фалес избрал день и час, когда длина собственной его тени равнялась его росту, в этот момент высота пирамиды должна также равняться длине отображенной ее тени. Задача греческого мудреца кажется сейчас нам очень простой, но надо помнить, что было это еще за 300 лет до жизни Евклида, который написал книгу, по которой обучаются геометрии до сих пор. Чтобы измерить высоту пирамиды по ее тени, надо было знать геометрические свойства треугольника: 1) что углы при основании равнобедренного треугольника равны, и обратно — что стороны , лежащие против равных углов треугольника, равны между собой. 2) что сумма углов всякого треугольника равна двум прямым углам (1800). Только вооруженный этим знанием Фалес вправе был заключить, что когда его собственная тень равна его росту, солнечные лучи встречают ровную почву под углом в половину прямого, и, следовательно, вершина пирамиды ,центр ее основания и конец ее тени должны обозначить равнобедренный треугольник. (Конечно, длину тени надо было считать от средней точки квадратного основания пирамиды; ширину этого основания Фалес мог измерить непосредственно).
о применении свойств треугольника — суммы углов треугольника в современной жизни Метод триангуляции Теорема о сумме углов треугольника активно «работает» в геодезии. На ней основан один из методов создания геодезической сети – метод триангуляции ( от лат. triangulum – треугольник). Состоит в построении рядов или сетей примыкающих друг к другу треугольников и в определении положения их вершин в избранной системе координат. В каждом треугольнике измеряют все три угла, а одну из его сторон определяют из вычислений путём последовательного решения предыдущих треугольников, начиная от того из них, в котором одна из его сторон получена из измерений.
Если сторона треугольника получена из непосредственных измерений, то она называется базисной стороной триангуляции. Для контроля и повышения точности измеряют большее число сторон, чем это необходимо. Считается, что метод триангуляции изобрёл и впервые применил В. Снеллиус (математик, физик и астроном) в 1615–17 гг. при прокладке ряда треугольников в Нидерландах для градусных измерений.
В работе «Голландский Эратосфен», опубликованной в 1617 году, В. Снеллиус описал метод триангуляции и привел результаты измерений дуги меридиана между двумя голландскими городами. В России применение этого метода для топографических съемок началось на рубеже XVII XIXвв., а к началуXXв. Он получил повсеместное распространение. Пример геодезического сигнала
Триангуляция имеет научное и практическое значение Она служит для: определения формы и размеров Земли методом градусных измерений; изучения горизонтальных движений земной коры; обоснования топографических съёмок в различных масштабах и целях; обоснования различных геодезических работ при изыскании; проектировании и строительстве крупных инженерных сооружений; при планировке и строительстве городов и т.д.
Как известно, каждая вышка постоянно посылает изменяющийся код, а телефон принимает его и отсылает обратно. Именно такая схема работы позволяет автоматически выбирать вышку через которую пойдет сигнал для наилучшего качества связи. Естественно, если вышек несколько, то можно применить метод триангуляции для вычисления точного положения телефона. А еще триангуляция – один из методов вычисления места нахождения абонента мобильной связи. Происходит это путем наложения координат абонента на карту местности
Видео:Как найти величины углов всех треугольников. Сумма углов треугольника. Геометрия 7 класс.Скачать

Сумма углов треугольника — определение и вычисление с доказательствами и примерами решения
Сумма углов треугольника:
Великий французский ученый XVII в. Блез Паскаль (1623—1662) еще в детстве любил изучать геометрические фигуры, открывать их свойства, измерять углы транспортиром.
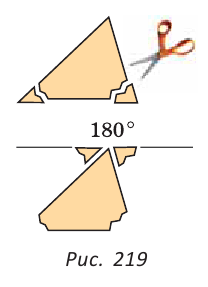
Юный исследователь заметил, что у любого треугольника сумма углов одна и та Ж6 180°. «Как же это объяснить?» — думал Паскаль. Тогда он отрезал у треугольника два уголка и приложил их к третьему (рис. 219). Получился развернутый угол, который, как известно, равен 180°. Это было его первое собственное открытие! Дальнейшая судьба мальчика была предопределена.
Теорема. Сумма углов треугольника равна 180°.
Дано: 
Доказать: 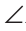
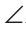
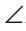
Доказательство:
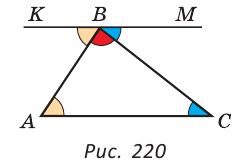
Через вершину В треугольника ABC проведем прямую КМ, параллельную стороне АС. Тогда 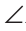
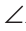
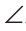
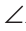





Следствия.
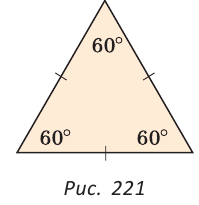
1. Каждый угол равностороннего треугольника равен 60°. (рис. 221).
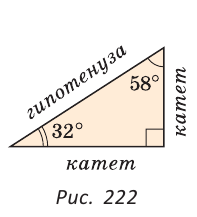
2. Сумма острых углов прямоугольного треугольника равна 90° (рис. 222).
В прямоугольном треугольнике стороны, заключающие прямой угол, называются катетами, сторона, противолежащая прямому углу, — гипотенузой (см. рис. 222).
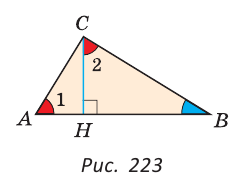
Проведем в прямоугольном треугольнике ABC высоту СН к гипотенузе АВ (рис. 223). Так как в треугольнике ABC угол 1 дополняет угол В до 90°, а в треугольнике СНВ угол 2 также дополняет угол В до 90°, то
Доказано свойство: «Угол между высотой прямоугольного треугольника, проведенной к гипотенузе, и катетом равен углу между другим катетом и гипотенузой».
Пример:
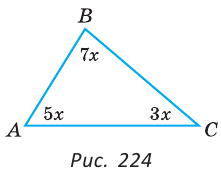
В треугольнике ABC градусные меры углов А, В и С относятся соответственно как 5:7:3. Найти углы треугольника (рис. 224).
Решение:
Пусть 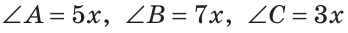
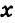
Так как сумма углов треугольника равна 180°, то
Тогда
Ответ:
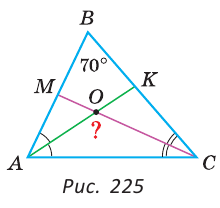
Пример:
В треугольнике ABC (рис. 225) угол В равен 70°, АК и СМ — биссектрисы, О — точка их пересечения. Найти угол АОС между биссектрисами.
Решение:
Сумма углов А и С треугольника ABC равна 180° — 70° = 110°. Так как биссектриса делит угол пополам, то
Из треугольника АОС находим:
Замечание. Если 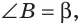
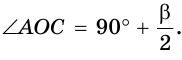
Пример:
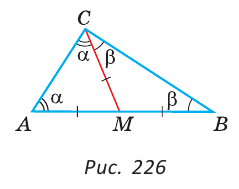
Доказать, что если медиана треугольника равна половине стороны, к которой она проведена, то данный треугольник — прямоугольный.
Доказательство:
Пусть СМ — медиана, 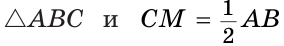
Докажем, что























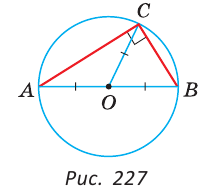
Замечание. Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным. На рисунке 227 это угол АСВ. Из задачи 3 следует свойство: «Вписанный угол, опирающийся на диаметр, — прямой».
Пример:
Доказать, что в прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы.
Доказательство:
Пусть в треугольнике ABC (рис. 228) 




Проведем отрезок СМ так, что










| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Внешний угол треугольника
- Свойство точек биссектрисы угла
- Свойство катета прямоугольного треугольника, лежащего против угла в 30°
- Четырехугольник и его элементы
- Перпендикулярные прямые в геометрии
- Признаки равенства треугольников
- Признаки равенства прямоугольных треугольников
- Соотношения в прямоугольном треугольнике
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
📹 Видео
7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

31. Теорема о сумме углов треугольникаСкачать

ГЕОМЕТРИЯ 7 класс : Сумма углов треугольникаСкачать

МЕРЗЛЯК-7 ГЕОМЕТРИЯ. СУММА УГЛОВ ТРЕУГОЛЬНИКА. ПАРАГРАФ-16, ЧАСТЬ-1Скачать

Сумма углов треугольника. Видеоурок 15. Геометрия 7 класс.Скачать

Сумма углов треугольника #геометрия #математикаСкачать

Теорема о сумме углов треугольника | Геометрия 7-9 класс #31 | ИнфоурокСкачать

Геометрия. 7 класс. Сумма углов треугольника. Внешний угол треугольника /28.01.2021/Скачать

Сумма углов треугольника. Геометрия 7 классСкачать