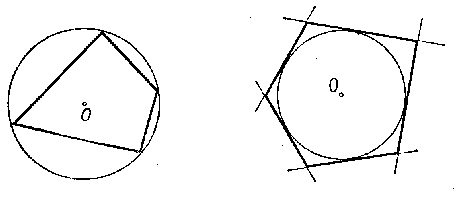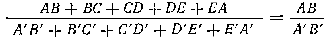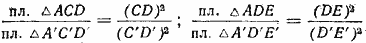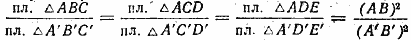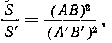Введем новое понятие: описанная окружность.
Определение: если все вершины многоугольника лежат на окружности, то окружность называется описанной около многоугольника, а многоугольник – вписанным в эту окружность.
На рисунке четырёхугольник MNKP вписан в окружность с центром O, так как все его вершины лежат на этой окружности.
На рисунке четырёхугольник ABCD не является вписанным в окружность, т.к. вершина C не лежит на окружности.
Рассмотрим треугольник АВС и впишем его в окружность. Всегда ли это возможно сделать?
Докажем теорему: Около любого треугольника можно описать окружность.
Дано: ∆ABC
Доказать: существует окружность, что A, B, C принадлежат этой окружности.
Доказательство:
Построим в треугольнике серединные перпендикуляры к сторонам и обозначим точку их пересечения О.
По свойству серединных перпендикуляров точка О равноудалена от точек А, В и С, т.е. OA = OB = OC.
Поэтому окружность с центром в точке О и радиусом ОА проходит через все три вершины треугольника, а значит является описанной около треугольника АВС.
Треугольник ABC вписан в окружность с центром O.
Что и требовалось доказать.
Четырехугольник, вокруг которого можно описать окружность обладает свойством: в любом вписанном четырёхугольнике сумма противоположных углов равна 180°.
Дано: ABCD вписанный четырехугольник.
Доказать:
∠B + ∠D = 180° и ∠A + ∠C = 180°.
Доказательство:
Рассмотрим вписанный угол АВС. Его градусная мера равна ∠ABC = 0,5 ∙ ∪ADC.
Градусная мера вписанного угла ADC равна ∠ADC = 0,5 ∙ ∪ABC.
Сумма углов АВС и ADC равна
∠ABC + ∠ADC = 0,5(∪ADC + ∪ABC) = 0,5 ∙ 360° = 180°.
Что и требовалось доказать.
Обратное утверждение также верно. Докажите его самостоятельно:
Если сумма противоположных углов четырехугольника равна 180°, то около него можно описать окружность.
Геометрия, 7-9: учеб. для общеобразоват. учреждений/ [Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др.]. – М.: Просвещение, 2017.
Видео:Многоугольники. Математика 8 класс | TutorOnlineСкачать

Многоугольники
Часть плоскости, ограниченная замкнутой ломаной линией, называется многоугольником.
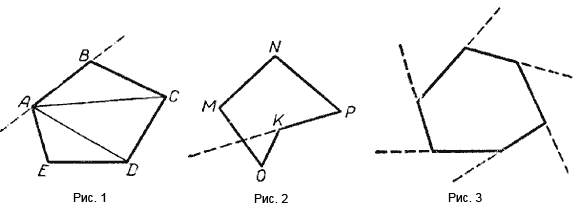
Отрезки этой ломаной линии называются сторонами многоугольника. АВ, ВС, CD, DE, ЕА (рис. 1) — стороны многоугольника ABCDE. Сумма всех сторон многоугольника называется его периметром.
Многоугольник называется выпуклым, если он расположен по одну сторону от любой своей стороны, неограниченно продолженной за обе вершины.
Многоугольник MNPKO (рис. 1) не будет выпуклым, так как он расположен не по одну сторону прямой КР.
Мы будем рассматривать только выпуклые многоугольники.
Углы, составленные двумя соседними сторонами многоугольника, называются его внутренними углами, а вершины их — вершинами многоугольника.
Отрезок прямой, соединяющий две несоседние вершины многоугольника, называется диагональю многоугольника.
АС, AD — диагонали многоугольника (рис. 2).
Углы, смежные с внутренними углами многоугольника, называются внешними углами многоугольника (рис. 3).
В зависимости от числа углов (сторон) многоугольник называется треугольником, четырёхугольником, пятиугольником и т. д.
Два многоугольника называются равными, если их можно совместить наложением.
Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Вписанные и описанные многоугольники
Если все вершины многоугольника лежат на окружности, то многоугольник называется вписанным в окружность, а окружность — описанной около многоугольника (рис).
Если все стороны многоугольника являются касательными к окружности, то многоугольник называется описанным около окружности, а окружность называется вписанной в многоугольник (рис).
Видео:Геометрия 8 класс (Урок№33 - Описанная окружность.)Скачать

Подобие многоугольников
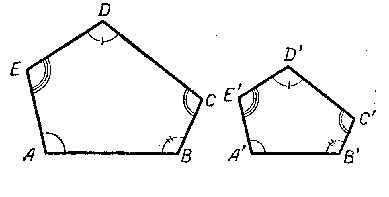
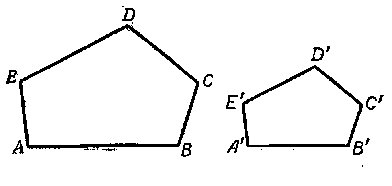
Два одноимённых многоугольника называются подобными, если углы одного из них соответственно равны углам другого, а сходственные стороны многоугольников пропорциональны.
Одноимёнными называются многоугольники, имеющие одинаковое число сторон (углов).
Сходственными называются стороны подобных многоугольников, соединяющие вершины соответственно равных углов (рис).
Так, например, чтобы многоугольник ABCDE был подобен многоугольнику A’B’C’D’E’, необходимо, чтобы: ∠A = ∠A’ ∠B = ∠B’ ∠С = ∠С’ ∠D = ∠D’ ∠Е = ∠Е’ и, кроме того, AB /A’B’ = BC /B’C’ = CD /C’D’ = DE /D’E’ = EA /E’A’.
Отношение периметров подобных многоугольников
Сначала рассмотрим свойство ряда равных отношений. Пусть имеем, например, отношения: 2 /1 = 4 /2 = 6 /3 = 8 /4 =2.
Найдем сумму предыдущих членов этих отношений, затем — сумму их последующих членов и найдём отношение полученных сумм, получим:
То же самое мы получим, если возьмём ряд каких-нибудь других отношений, например: 2 /3 = 4 /6 = 6 /9 = 8 /12 = 10 /15= 2 /3 Найдем сумму предыдущих членов этих отношений и сумму последующих, а затем найдём отношение этих сумм, получим:
В том и другом случае сумма предыдущих членов ряда равных отношений относится к сумме последующих членов этого же ряда, как предыдущий член любого из этих отношений относится к своему последующему.
Мы вывели это свойство, рассмотрев ряд числовых примеров. Оно может быть выведено строго и в общем виде.
Теперь рассмотрим отношение периметров подобных многоугольников.
Пусть многоугольник ABCDE подобен многоугольнику A’B’C’D’E’ (рис).
Из подобия этих многоугольников следует, что
На основании выведенного нами свойства ряда равных отношений можем написать:
Сумма предыдущих членов взятых нами отношений представляет собой периметр первого многоугольника (Р), а сумма последующих членов этих отношений представляет собой периметр второго многоугольника (Р’), значит, P /P’ = AB /A’B’ .
Следовательно, периметры подобных многоугольников относятся как их сходственные стороны.
Отношение площадей подобных многоугольников
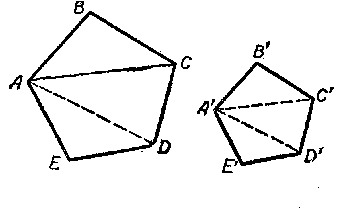
Пусть ABCDE и A’B’C’D’E’ — подобные многоугольники (рис).
Известно, что ΔAВС
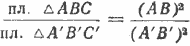
Так как вторые отношения этих пропорций равны, что вытекает из подобия многоугольников, то
Используя свойство ряда равных отношений получим:
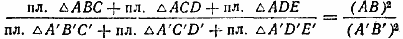
где S и S’ — площади данных подобных многоугольников.
Следовательно, площади подобных многоугольников относятся как квадраты сходственных сторон.
Полученную формулу можно преобразовать к такому виду: S /S’ = ( AВ /A’В’ ) 2
Площадь произвольного многоугольника
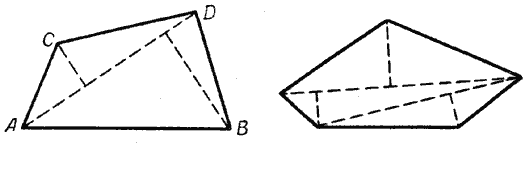
Пусть требуется вычислить площадь произвольного четырёхугольника АВDС (рис).
Проведём в нём диагональ, например АD. Получим два треугольника АВD и АСD, площади которых вычислять умеем. Затем находим сумму площадей этих треугольников. Полученная сумма и будет выражать площадь данного четырёхугольника.
Если нужно вычислить площадь пятиугольника, то поступаем таким же образом: из одной какой-нибудь вершины проводим диагонали. Получим три треугольника, площади которых можем вычислить. Значит, можем найти и площадь данного пятиугольника. Так же поступаем при вычислении площади любого многоугольника.
Площадь проекции многоугольника
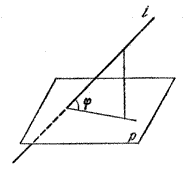
Напомним, что углом между прямой и плоскостью называется угол между данной прямой и ее проекцией на плоскость (рис.).
Теорема. Площадь ортогональной проекции многоугольника на плоскость равна площади проектируемого многоугольника, умноженной на косинус угла, образованного плоскостью многоугольника и плоскостью проекции.
Каждый многоугольник можно разбить на треугольники, сумма площадей которых равна площади многоугольника. Поэтому теорему достаточно доказать для треугольника.
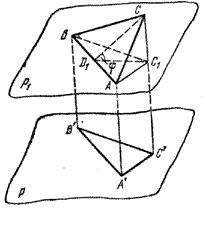
Пусть ΔАВС проектируется на плоскость р. Рассмотрим два случая:
а) одна из сторон ΔАВС параллельна плоскости р;
б) ни одна из сторон ΔАВС не параллельна р.
Рассмотрим первый случай: пусть [АВ] || р.
Проведем через (АВ) плоскость р1 || р и спроектируем ортогонально ΔАВС на р1 и на р (рис.); получим ΔАВС1 и ΔА’В’С’ .
По свойству проекции имеем ΔАВС1 (cong) ΔА’В’С’, и поэтому
Проведем [CD1] ⊥ [AB] и отрезок D1C1. Тогда [D1C1] ⊥ [AB], a ( overbrace) = φ есть величина угла между плоскостью ΔАВС и плоскостью р1. Поэтому
и, следовательно, SΔ A’B’C’ = SΔ ABC cos φ.
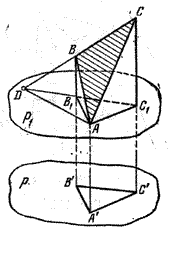
Перейдем к рассмотрению второго случая. Проведем плоскость р1 || р через ту вершину ΔАВС, расстояние от которой до плоскости р наименьшее (пусть это будет вершина А).
Спроектируем ΔАВС на плоскости р1 и р (рис.); пусть его проекциями будут соответственно ΔАВ1С1 и ΔА’В’С’.
SΔ A’B’C’ = SΔAB 1 C 1 = SΔADC 1 — SΔADB 1 = ( SΔADC — SΔADB) cos φ = SΔ ABC cos φ
Видео:МногоугольникСкачать

Вписанные и описанные многоугольники.
Определение. Если все стороны многоугольника касаются окружности, то многоугольник называется описанным около окружности, а окружность – вписанной в многоугольник.
Определение. Если все вершины многоугольника лежат на окружности, то многоугольник называется вписанным в эту окружность, а окружность – описанной около треугольника.
| Вписанная окружность | Описанная окружность |
Треугольник 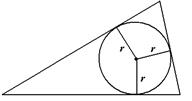 Центр – точка пересечения биссектрис. Центр – точка пересечения биссектрис. 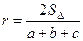 . . | 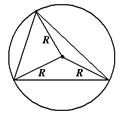 Центр – точка пересечения серединных перпендикуляров. Центр – точка пересечения серединных перпендикуляров. 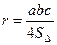 . . |
| Параллелограмм НЕТ | НЕТ |
Ромб 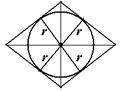 Центр – точка пересечения диагоналей. Радиус окружности равен половине высоты ромба, т.е. Центр – точка пересечения диагоналей. Радиус окружности равен половине высоты ромба, т.е. 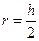 . . | НЕТ |
| Прямоугольник НЕТ | 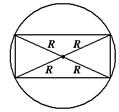 Центр – точка пересечения диагоналей. Радиус окружности равен половине длины диагонали прямоугольника, т.е. Центр – точка пересечения диагоналей. Радиус окружности равен половине длины диагонали прямоугольника, т.е. 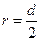 . . |
Квадрат 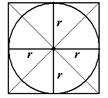 Центр – точка пересечения диагоналей. Радиус окружности равен половине длины стороны квадрата, т.е. Центр – точка пересечения диагоналей. Радиус окружности равен половине длины стороны квадрата, т.е. 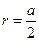 . . | 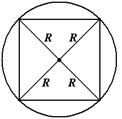 Центр – точка пересечения диагоналей. Радиус окружности равен половине длины диагонали квадрата, т.е. Центр – точка пересечения диагоналей. Радиус окружности равен половине длины диагонали квадрата, т.е. 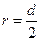 . . |
Трапеция 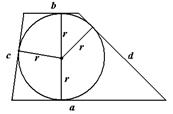 Центр – точка пересечения биссектрис. В трапецию можно вписать окружность тогда и только тогда, когда суммы длин противоположных сторон равны, т.е. Центр – точка пересечения биссектрис. В трапецию можно вписать окружность тогда и только тогда, когда суммы длин противоположных сторон равны, т.е. 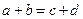 . Радиус окружности равен половине длины высоты трапеции, т.е. . Радиус окружности равен половине длины высоты трапеции, т.е. 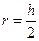 . . | 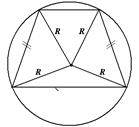 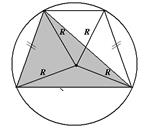 Центр – точка пересечения серединных перпендикуляров. Около трапеции можно описать окружность тогда и только тогда, когда трапеция равнобедренная. Радиус окружности можно найти как радиус описанной окружности около треугольника, вершинами которого являются вершины трапеции (любые три из четырех у трапеции). Центр – точка пересечения серединных перпендикуляров. Около трапеции можно описать окружность тогда и только тогда, когда трапеция равнобедренная. Радиус окружности можно найти как радиус описанной окружности около треугольника, вершинами которого являются вершины трапеции (любые три из четырех у трапеции). |
Произвольный выпуклый четырехугольник 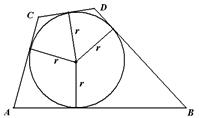 Центр – точка пересечения биссектрис. В произвольный выпуклый четырехуголь-ник можно вписать окружность тогда и только тогда, когда суммы длин противоположных сторон равны, т.е. Центр – точка пересечения биссектрис. В произвольный выпуклый четырехуголь-ник можно вписать окружность тогда и только тогда, когда суммы длин противоположных сторон равны, т.е. 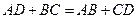 . Общего способа и формулы для вычисления длины радиуса нет. . . Общего способа и формулы для вычисления длины радиуса нет. . | 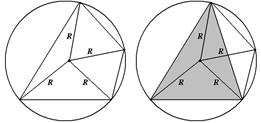 Центр – точка пересечения серединных перпендикуляров. Около произвольного выпуклого четырехугольника можно описать окружность тогда и только тогда, когда суммы противоположных углов равны Центр – точка пересечения серединных перпендикуляров. Около произвольного выпуклого четырехугольника можно описать окружность тогда и только тогда, когда суммы противоположных углов равны 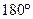 . Радиус окружности можно найти как радиус описанной окружности около треугольника, вершинами которого являются вершины данного четырехугольника (любые три из его четырех). Теорема 39. (Птолемея). В четырехуголь-нике, вписанном в окружность, произведение диагоналей равно сумме произведений противоположных сторон. . Радиус окружности можно найти как радиус описанной окружности около треугольника, вершинами которого являются вершины данного четырехугольника (любые три из его четырех). Теорема 39. (Птолемея). В четырехуголь-нике, вписанном в окружность, произведение диагоналей равно сумме произведений противоположных сторон. 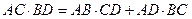 |
Определение. Выпуклый многоугольник называется правильным, если у него все углы равны и стороны равны.
Теорема 38. Около любого правильного многоугольника можно описать окружность и притом только одну.
Теорема 39. В любой правильный многоугольник можно вписать окружность и притом только одну.
💥 Видео
Правильные многоугольники. Урок 11. Геометрия 9 классСкачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

9 класс, 22 урок, Окружность, описанная около правильного многоугольникаСкачать

8 класс, 2 урок, Выпуклый многоугольникСкачать

Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Сумма внутренних углов многоугольника. Выпуклые и невыпуклые многоугольники. 8 класс.Скачать

Геометрия 9 класс (Урок№21 - Правильный многоугольник. Описанная и вписанная окружность.)Скачать

9 класс, 23 урок, Окружность, вписанная в правильный многоугольникСкачать

9 класс, 24 урок, Формулы для вычисления площади правильного многоугольника, его стороныСкачать

Окружность, описанная около правильного многоугольника | Геометрия 7-9 класс #105 | ИнфоурокСкачать

Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

8 класс, 39 урок, Описанная окружностьСкачать

9 класс. Правильный многоугольник, вписанный в окружность и описанный около окружностиСкачать
Окружность №16 из ОГЭ. Вписанные и описанные многоугольники. Квадрат и окружность.Скачать