Если прямая параллельна линии пересечения двух плоскостей и не принадлежит

10 класс. Геометрия. Параллельные прямые в пространстве. Решение задач

• Оглавление
• Занятия
• Обсуждение
• О курсе

Вопросы

Задай свой вопрос по этому материалу!

Поделись с друзьями

Комментарии преподавателя

Видео:Параллельность прямой к плоскостиСкачать

Определение параллельных прямых

Определение: две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются (рис. 1).

Рис. 1. Параллельные прямые

Видео:10 класс, 6 урок, Параллельность прямой и плоскостиСкачать

Лемма

Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.

Пояснение к лемме

Даны две параллельные прямые а и b. Прямая а пересекает плоскость в точке М. Лемма утверждает, что прямая b тоже пересекает плоскость в некоторой точке, назовем ее N (рис. 2).

Рис. 2. Иллюстрация к лемме

Видео:Параллельность прямой и плоскости. 10 класс.Скачать

Определение параллельности прямой и плоскости

Определение. Прямая и плоскость называются параллельными, если они не имеют общих точек.

Видео:Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

Признак параллельности прямой и плоскости

Теорема (признак параллельности прямой и плоскости)

Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости.

Пояснение к признаку.

Дана плоскость , прямая b лежит в плоскости α, прямая а параллельна прямой b, прямая а не лежит в плоскости (рис. 3). Согласно признаку параллельности прямой и плоскости, прямая а параллельна всей плоскости α. Мощь этого признака в том, что только из того, что прямая а не имеет общих точек с прямой b (небольшой частью всей плоскости), следует, что прямая а не имеет общих точек со всей плоскостью.

Рис. 3. Иллюстрация к признаку

Следующее утверждение часто используется для решения задач.

Видео:Пересечение двух плоскостей. Плоскости в виде треугольникаСкачать

Утверждение 1

Если плоскость проходит через данную прямую а, параллельную другой плоскости (а || ), и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой: a || b.

Дана плоскость и прямая а, которая параллельна плоскости (рис. 4). Через прямую а проходит плоскость , которая пересекает плоскость по некоторой прямой b . Согласно утверждению, линия пересечения плоскостей и – прямая b будет параллельна прямой а.

Рис. 4. Иллюстрация к утверждению

Видео:Линия пересечения плоскостейСкачать

Задача 1

Треугольники ABC и ABD не лежат в одной плоскости. Докажите, что любая прямая, параллельная отрезку СD, пересекает плоскости данных треугольников.

Рис. 5. Иллюстрация к задаче

Нам дано, что точка D не лежит в плоскости АВС, а точка С не лежит в плоскости АВD. Нужно доказать, что любая прямая, назовем ее m, параллельная прямой СD, пересечет плоскости АВС и АВD.

Вспомним лемму, если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.

Прямая СD пересекает плоскость АВС в точке С. Значит, и параллельная ей прямая m пересечет эту плоскость в некоторой точке N (по лемме): .

Прямая СD пересекает плоскость ABD в точке D. Значит, и параллельная ей прямая m пересечет эту плоскость в некоторой точке M (по лемме):.

Видео:Геометрия 10 класс (Урок№6 - Параллельность плоскостей.)Скачать

Задача 2

Точки А и В лежат в плоскости , а точка С не лежит в этой плоскости. Докажите, что прямая, проходящая через середины отрезков АС и ВС, параллельна плоскости .

Рис. 6. Иллюстрация к задаче

Пусть M – середина АС, N- середина ВС.

Точка М не лежит в плоскости , так как если бы она в ней лежала, то и прямая АМ, а значит и точка С, лежала бы в плоскости , что противоречит условию. Аналогично, точка N не лежит в плоскости

Рассмотрим треугольник АВС. MN – средняя линия в этом треугольнике. По свойству, MN параллельна АВ. Прямая MN параллельна прямой АВ, а прямая АВ лежит в плоскости . Значит, прямая АВ параллельна плоскости, что и требовалось доказать.

Видео:Математика без Ху!ни. Взаимное расположение прямой и плоскости.Скачать

Задача 3

Плоскость параллельна стороне ВС треугольника АВС и проходит через середину стороны АВ. Докажите, что плоскость проходит через середину стороны АС.

Рис. 7. Иллюстрация к задаче

Нам даны две плоскости АВС и . Они не совпадают, имеют общую точку M, а значит, имеют линию пересечения MN. Докажем, что N – середина АС.

Плоскость АВС проходит через прямую ВС, которая по условию параллельна плоскости . Значит, ВС параллельна линии пересечения плоскостей MN.

Параллельные прямые MN и АС рассекают стороны угла А на пропорциональные части, то есть АМ : МВ = АN : NС = 1. Значит, N – середина стороны АС, что и требовалось доказать.

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Итоги урока

Итак, мы повторили теорию и рассмотрели решение более сложных задач по теме: «Параллельность прямой и плоскости». На следующем уроке мы рассмотрим взаимное расположение прямых в пространстве.

Видео:Построение линии пересечения двух плоскостейСкачать

Самостоятельная работа «Параллельность прямых и плоскостей»

Видео:02. Построение прямой пересечения двух плоскостейСкачать

«Календарь счастливой жизни:
инструменты и механизм работы
для достижения своих целей»

Сертификат и скидка на обучение каждому участнику

ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ

Точки М, Р, К – середины ребер DA , DB , DC тетраэдра DABC . Назовите прямую, параллельную плоскости FBC

1) МР 2) РК 3) МК 4) МК и РК

АВС DA ₁ B ₁ C ₁ D ₁ – прямоугольный параллелепипед. Какая из прямых параллельна плоскости A ₁ B ₁ C ₁ ?

В тетраэдре D АВС ВК = КС, DP = PC . Плоскости какой грани параллельна прямая РК?

1) DAB 2) DBC 3) DAC 4) ABC

Выберите верные высказывания:

1) Две прямые в пространстве называются параллельными, если они не пересекаются.

2) Если одна из двух параллельных прямых параллельна плоскости, то другая прямая либо так же ей параллельна, либо лежит в этой плоскости.

3) Существует такая прямая, которая лежит в плоскости и параллельна прямой, пересекающей данную плоскость.

4) Скрещивающиеся прямые не имеют общих точек.

Определите взаимное расположение прямых.

1) a и b – пересекающиеся прямые

2) a и b – параллельные прямые

3) a и b – скрещивающиеся прямые

6 6. Могут ли прямая и плоскость иметь одну общую точку?

7. Верно ли, что если прямая не имеет с плоскостью общих точек, то эта прямая параллельна плоскости?

8. Верно ли, что любые четыре точки не лежат в одной плоскости?

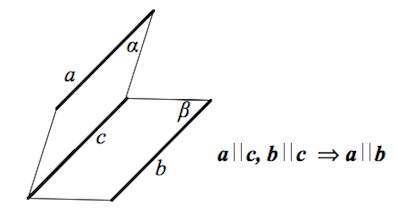
9. Верно ли, что две прямые a и b перпендикулярны друг другу, если a II c и b II c ?

10. Верно ли, что линия пересечения двух плоскостей параллельна одной из этих плоскостей

11. Верно ли, что если две стороны треугольника параллельны плоскости α, то и третья сторона параллельна плоскости α?

12. Верно ли, что если прямая с пересекает прямую a и не пересекает прямую b , параллельную прямой a , то b и c – скрещивающиеся прямые?

13. Две стороны параллелограмма параллельны плоскости α. Параллельны ли плоскость α и плоскость параллелограмма

14. Могут ли быть равны два непараллельных отрезка, заключенные между параллельными плоскостями?

15. Могут ли пересекаться плоскости, параллельные одной и той же прямой?

ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ

Точки М, Р, К – середины ребер DA , DB , DC тетраэдра DABC . Назовите прямую, параллельную плоскости F А B .

1) МР 2) РК 3) МК 4) МК и РК

АВС DA ₁ B ₁ C ₁ D ₁ – прямоугольный параллелепипед. Какая из прямых параллельна плоскости A ₁ AD ?

В тетраэдре D АВС AM = MD, AN = NB. Плоскости какой грани параллельна прямая MN ?

1) DAB 2) DBC 3) DAC 4) ABC

Выберите верные высказывания:

1) Параллельные прямые не имеют общих точек.

2) Если прямая параллельна данной плоскости, то она параллельна любой прямой, лежащей в этой плоскости.

3) Если прямая параллельна линии пересечения двух плоскостей и не принадлежит ни одной из них, то она параллельна каждой из этих плоскостей.

4) Существует параллелепипед, у которого все углы граней острые.

Определите взаимное расположение прямых.

1) a и b – пересекающиеся прямые

2) a и b – параллельные прямые

3) a и b – скрещивающиеся прямые

6. Могут ли прямая и плоскость иметь множество общих точек?

7. Верно ли, что через две параллельные прямые всегда можно провести плоскость?

8. Верно ли, что любые четыре точки лежат в одной плоскости?

9. Верно ли, что если прямые не пересекаются, то они скрещиваются?

10. Верно ли, что плоскости α и β параллельны, если две пересекающиеся прямые m и n плоскости α параллельны плоскости β?

11. Может ли каждая из двух скрещивающихся прямых быть параллельна третьей прямой?

12. Верно ли, что если плоскость содержит данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой?

13. Верно ли, что если две прямые параллельны некоторой плоскости, то они параллельны друг другу?

14. Верно ли утверждение, что плоскости параллельны, если две прямые, лежащие в одной плоскости, соответственно параллельны двум прямым другой плоскости?

15. Прямые a и c параллельны, а прямые b и a пересекаются. Могут ли прямые b и c быть параллельными?

ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ

Видео:Лекция 5. Взаимное расположение двух прямых, прямой и плоскости, двух плоскостейСкачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 966 человек из 79 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 340 человек из 71 региона

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 690 человек из 74 регионов

Ищем педагогов в команду «Инфоурок»

• Морозова Юлия ВасильевнаНаписать 41454 05.11.2017

Номер материала: ДБ-828856

05.11.2017 348

05.11.2017 243

05.11.2017 482

05.11.2017 413

05.11.2017 279

05.11.2017 249

05.11.2017 315

05.11.2017 3285

Не нашли то, что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Госдуме предложили продлить каникулы для школьников до 16 января

Время чтения: 1 минута

Глава СПЧ предложил ввести подготовительные курсы перед обучением в школе для детей мигрантов

Время чтения: 1 минута

ОНФ планирует решить проблему с низкими зарплатами водителей школьных автобусов в России

Время чтения: 1 минута

В России разработают рекомендации по сопровождению студентов с ОВЗ

Время чтения: 2 минуты

В Минпросвещения рассказали о формате обучения школьников после праздников

Время чтения: 1 минута

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:Пересечение прямой и плоскостиСкачать

Параллельность прямых и плоскостей

Видео:Взаимное пересечение двух плоскостейСкачать

Параллельные прямые

Параллельные прямые – прямые, которые лежат в одной плоскости и не пересекаются.

Признак параллельности прямых

Две прямые, параллельные третьей, параллельны между собой.

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Параллельные прямая и плоскость

Прямая и плоскость называются параллельными , если они не имеют общих точек.

Признак параллельности прямой и плоскости

Если прямая, не принадлежащая данной плоскости, параллельна какой-нибудь прямой этой плоскости, то она параллельна этой плоскости.

Свойство прямой, параллельной данной плоскости

Если плоскость β проходит через прямую a , параллельную плоскости α , и пересекает эту плоскость по прямой b , то b || a .

Видео:Нахождение линии пересечения плоскостей путём приглашения плоскостей посредниковСкачать

Параллельные плоскости

Параллельные плоскости – плоскости, которые не пересекаются.

Признаки параллельности плоскостей

Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то такие плоскости параллельны.

Если каждая из двух данных плоскостей параллельна третьей плоскости, то данные две плоскости параллельны между собой.

Свойства параллельных плоскостей

Если две параллельные плоскости пересекаются третьей плоскостью, то линии пересечения плоскостей параллельны.

Отрезки параллельных прямых, заключенные между двумя параллельными плоскостями, равны.

Чтобы не потерять страничку, вы можете сохранить ее у себя:

🔍 Видео

ПАРАЛЛЕЛЬНОСТЬ ПРЯМОЙ и ПЛОСКОСТИ 10 11 класс стереометрияСкачать

Параллельность прямых и плоскостей в пространстве. Практическая часть - решение задачи. 10 класс.Скачать

№25. Докажите, что если данная прямая параллельна прямой, по которой пересекаютсяСкачать

Параллельность прямых. 10 класс.Скачать