Пирамида – многогранник, основание которого — многоугольник , а остальные грани — треугольники, имеющие общую вершину.
По числу углов основания различают пирамиды треугольные , четырёхугольные и т. д.
Вершина пирамиды — точка, соединяющая боковые рёбра и не лежащая в плоскости основания.
Основание — многоугольник, которому не принадлежит вершина пирамиды.
Апофема — высота боковой грани правильной пирамиды, проведенная из ее вершины.
Высота — отрезок перпендикуляра, проведённого через вершину пирамиды к плоскости её основания (концами этого отрезка являются вершина пирамиды и основание перпендикуляра).
Диагональное сечение пирамиды — сечение пирамиды, проходящее через вершину и диагональ основания.
Видео:№252. Основанием пирамиды DABC является равнобедренный треугольник ABC, в котором АВ = АС, ВС=6 смСкачать
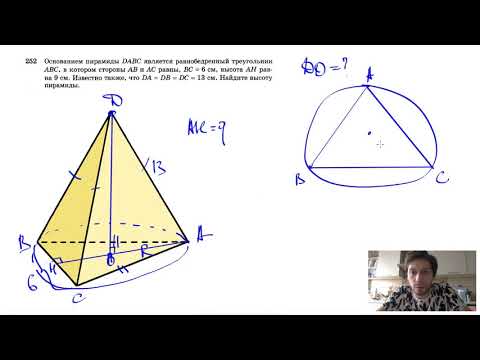
Некоторые свойства пирамиды
1) Если все боковые ребра равны, то
– около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр
– боковые ребра образуют с плоскостью основания равные углы
Верно и обратное.
Если боковые ребра образуют с плоскостью основания равные углы, то все боковые ребра пирамиды равны.
Если около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр, то все боковые ребра пирамиды равны.
2) Если все грани пирамиды наклонены к плоскости основания под одним углом , то в основание пирамиды можно вписать окружность, причём вершина пирамиды проецируется в её центр
Верно и обратное.
Видео:№250. Основанием пирамиды является равнобедренный треугольник с углом 120°. Боковые ребраСкачать
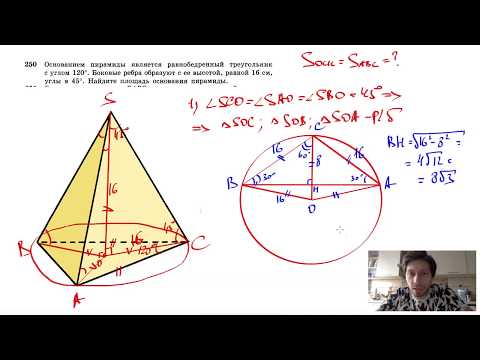
Виды пирамид
Пирамида называется правильной , если основанием её является правильный многоугольник, а вершина проецируется в центр основания.
Для правильной пирамиды справедливо:
– боковые ребра правильной пирамиды равны;
– в правильной пирамиде все боковые грани — равные равнобедренные треугольники;
– в любую правильную пирамиду можно вписать сферу;
– около любой правильной пирамиды можно описать сферу;
– площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.
Видео:Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать

Пирамида называется прямоугольной , если одно из боковых рёбер пирамиды перпендикулярно основанию. Тогда это ребро и есть высота пирамиды.
Усечённой пирамидой называется многогранник, заключённый между основанием пирамиды и секущей плоскостью, параллельной её основанию.
Тетраэдр – треугольная пирамида. В тетраэдре любая из граней может быть принята за основание пирамиды.
Видео:Геометрия 7 класс (Урок№13 - Равнобедренный треугольник.)Скачать

Если основание пирамиды равнобедренный треугольник
| Учебный курс | Решаем задачи по геометрии |
| Задача. В основании пирамиды лежит равнобедренный треугольник с боковой стороной b и углом при основании β. все боковые грани образуют с основанием угол φ. Решение. При желании можно разбить треугольник ABC на два прямоугольных треугольника AKB и AKC. Но в результате формулы будут все равно тождественны. Действительно, AK = AB sin ß = b sin β откуда Если воспользоваться основными тригонометрическими тождествами, то Теперь найдем площадь боковой поверхности пирамиды. Учитывая, что BC = 2BK, то BC = 2b cos β Таким образом, радиус вписанной окружности в основание пирамиды будет равен Теперь определим высоту боковых граней пирамиды. Зная, что Тогда площадь грани пирамиды, прилегающей к равным сторонам основания (а в основании пирамиды у нас лежит равнобедренный треугольник) будет равна: Площадь боковой грани, прилегающей к основанию, равна: Площадь боковой поверхности пирамиды равна: Откуда площадь полной поверхности пирамиды с равнобедренным треугольником в основании составит: Видео:№107. В равнобедренном треугольнике основание в два раза меньше боковой стороны, а периметрСкачать  Решение задач с использованием свойств различных видов пирамидРазделы: Математика Изучение пирамиды и ее элементов представляет широкие возможности для составления и решения задач на различных видах пирамид по следующим темам:
Действующие учебники геометрии либо не содержат , либо содержат в недостаточном количестве задачи по этим темам. Как показала практика, учащиеся с большим интересом принимают участие не только в решении данных задач, но и в их составлении. Они с удовольствием предлагают различные решения придуманных ими задач. К этому учащихся необходимо подводить хорошо продуманной системой теоретических положений и практических упражнений. Учебники Л.С. Атанасяна и др. “Геометрия 10–11” и А.В.Погорелова “Геометрия 10–11” содержат опорный теоретический материал по теме “Пирамида и ее элементы”. В дополнение к нему можно рассмотреть следующие свойства часто встречающихся видов пирамид. Теория.
б) все боковые ребра пирамиды равны между собой.
в) все боковые ребра пирамиды равны между собой.
б) все боковые ребра пирамиды составляют с плоскостью ее основания равные между собой углы.
Теоремы о пирамидах, в которых одна или две боковые грани перпендикулярны плоскости основания.
Задачи для решения. Задания из книги “Самостоятельные и контрольные работы по геометрии для 11-го класса” Ершовой А.П., Голобородько В.В. Пирамиды, в которых основание высоты является центром описанной или вписанной окружности основания пирамиды. Вариант А.
б) Докажите равенство отрезков АО, ВО, СО и ДО. в) Обоснуйте положение точки О в прямоугольнике АВСД и найдите длину высоты SO.
б) обоснуйте положение основания высоты пирамиды в данном равнобедренном треугольнике. в) Найдите высоту пирамиды. Вариант Б.
б) Определите, при каких значениях ? высота пирамиды будет находиться вне пирамиды. в) Найдите высоту пирамиды.
б) Найдите высоту пирамиды. в) Двумя способами – путем вычисления площадей боковых граней и с помощью теоремы об ортогональной проекции многоугольника – найдите боковую поверхность пирамиды. Сравните полученные результаты. Вариант В.
б) При каких условиях высота пирамиды лежит внутри пирамиды? в) Найдите высоту пирамиды. г) Найдите площадь основания пирамиды.
б) Найдите высоту трапеции, лежащей в основании пирамиды.
Пирамиды, в которых одна или две боковые грани перпендикулярны плоскости основания. Вариант А.
б) Обоснуйте угол в) Найдите площадь третьей боковой грани. г) Найдите боковую поверхность пирамиды.
б) Обоснуйте углы наклона, равные в) Докажите, что основание высоты пирамиды равноудалено от двух сторон правильного треугольника, и обоснуйте положение основания высоты на стороне правильного треугольника. г) Найдите боковую поверхность пирамиды. Вариант Б.
б ) Обоснуйте углы, равные в ) Докажите, что боковые грани пирамиды попарно равны. г ) Найдите боковую поверхность пирамиды.
б) Обоснуйте положение основания высоты пирамиды. в) Найдите высоту пирамиды. г) Найдите боковую поверхность пирамиды. Вариант В.
б) Обоснуйте углы, равные в) Найдите боковую поверхность пирамиды.
б) Обоснуйте положение основания высоты пирамиды. в) Найдите площадь основания пирамиды. г) Найдите боковую поверхность пирамиды. Пирамиды, в которых заданы расстояния между точками и элементами пирамиды. Вариант А.
б ) Найдите площадь основания пирамиды.
Вариант Б.
б ) Найдите площадь основания пирамиды. Вариант В.
Указанный в статье перечень задач может быть расширен Вами и вашими учениками. 📸 ВидеоРавнобедренный треугольник. Определение. Свойства. Теоремы и доказательства.Скачать  Равнобедренный треугольник. 7 класс.Скачать  7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать  №243. Основанием пирамиды DABC является треугольник ABC, у которого АВ = АС= 13 см, ВС=10 см; реброСкачать 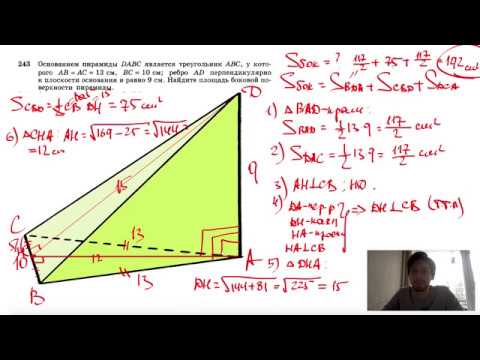 №239. Основанием пирамиды является ромб, сторона которого равна 5 см, а одна из диагоналейСкачать  №253. Основанием пирамиды является равнобедренная трапеция с основаниями 6 см и 4√6 смСкачать 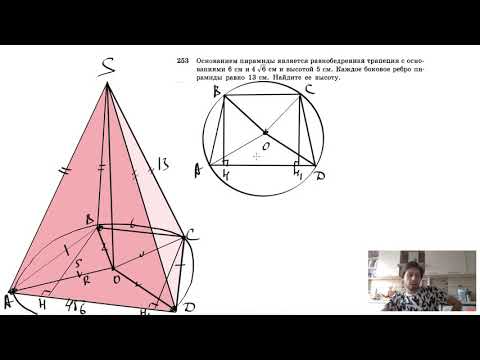 №255. В равнобедренном треугольнике CDE с основанием СЕ проведена высота CF.Скачать  №251. Основанием пирамиды DABC является прямоугольный треугольник с гипотенузой ВС. БоковыеСкачать  Сможешь найти основание? Задача про медиану равнобедренного треугольникаСкачать  Равнобедренный треугольникСкачать  Пирамиды, в которых высота проходит через центр описанной около основания окружностиСкачать 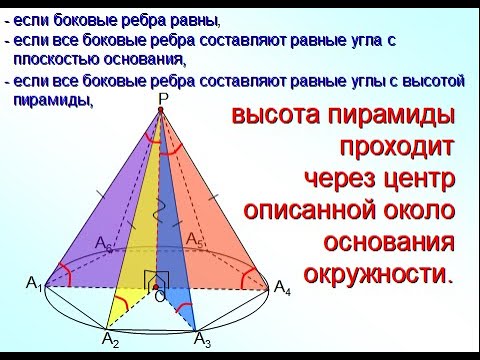 Делаем модель пирамиды для решения задачи по стереометрииСкачать  №249. В равнобедренном треугольнике одна сторона равна 25 см, а другая равна 10 см. Какая изСкачать  Построение равнобедренного треугольникаСкачать  №109. В равнобедренном треугольнике ABC с основанием ВС проведена медиана AM. Найдите медиану AMСкачать 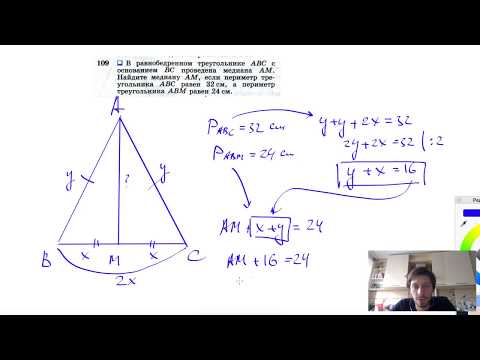 |













 . Все двугранные углы при основании пирамиды равны
. Все двугранные углы при основании пирамиды равны  .
. .
.