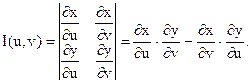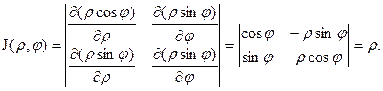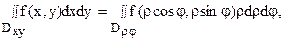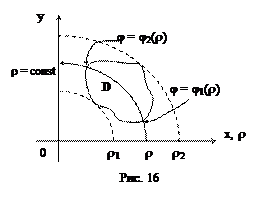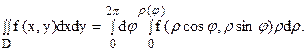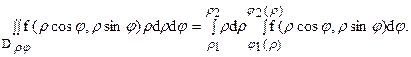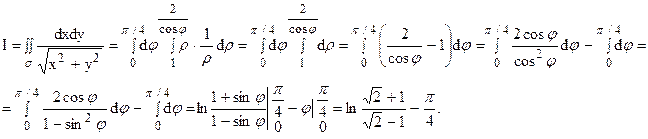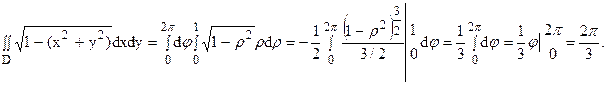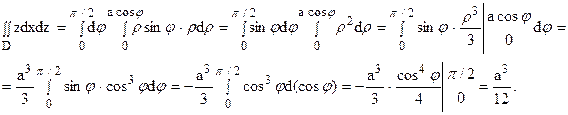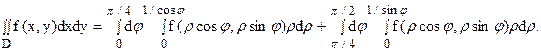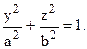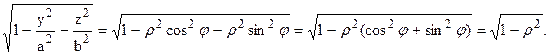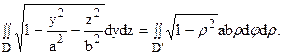Если область d ограничена окружностями (7 видео)

Замена переменных в двойном интеграле. Вычисление двойных интегралов в полярных координатах.

( 7)

При вычислении двойных интегралов иногда бывает полезно сделать замену переменных. Пусть

( 8)

функции, определенные на всей плоскости xOy или в некоторой ее области D_xy и имеющие непрерывные частные производные в области D_xy. Допустим также, что систему уравнений ( 7) можно однозначно разрешить относительно x и y:

Тогда каждой точке М(x;y) из области D_xy будет взаимно однозначно соответствовать пара чисел (u,v), называемых криволинейными координатами этой точки. Если область D_xy расположена в той части плоскости xOy, в которой введены криволинейные координаты u, v, то справедлива следующая формула:

( 9)

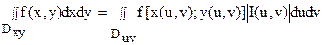
где D_uv – область изменения криволинейных координат u и v, отвечающая области D_xy, а I(u,v) – якобиан преобразования ( 8):

( 10)

Например, для полярных координат имеем:

В зависимости от строения области интегрирования или подынтегральной функции вычисление двойного интеграла может оказаться более простым не в прямоугольной, а в какой-нибудь из криволинейных систем координат. Наиболее распространенной из них является полярная.

Для того, чтобы преобразовать двойной интеграл в прямоугольных декартовых координатах в двойной интеграл в полярных координатах, нужно x и y в подынтегральной функции заменить соответственно через rcosj и rsinj, а выражение dxdy заменить выражением rdrdj:

( 11)

где D_r_j – та же область D_ху, но описанная в полярных координатах (поскольку в этом случае якобиан I = r).

В этой формуле следует обратить внимание на то, что в подынтегральной функции не только происходит замена координат по формулам перехода от декартовых к полярным, но и появляется дополнительный множитель r.

Вычисление двойного интеграла в полярной системе координат, также как и в декартовой, сводится к двукратному интегрированию, но, соответственно, по переменным r и j. Расстановку пределов при вычислении интегралов в полярных координатах можно производить, используя чертеж области интегрирования на плоскости Oxy и геометрический смысл полярных координат.

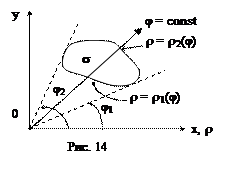
Пусть, например, внешнее интегрирование производится по j и область D_ρφ является правильной в направлении j = сonst, т.е. каждый луч, выходящий из начала координат, пересекает область D_ρφ по отрезку
(рис. 14).

Тогда справедлива формула:

(12)

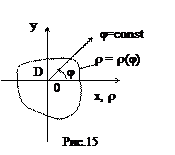
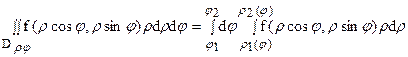
В частном случае, когда D содержит начало координат, имеем:

( 13)

Если же внешнее интегрирование производится по r и область D_ρφ является правильной в направлении
r = const, т.е. каждая окружность пересекает, имея центром начало координат, область D_ρφ по дуге этой окружности (только в двух точках) (см. рис.16), то справедлива формула:

( 14)

Пример 12.

Вычислить двойной интеграл по области, ограниченной линиями: x 2 + y 2 = 1, y = 0, x = 2, y = x и лежащей в первом квадранте.

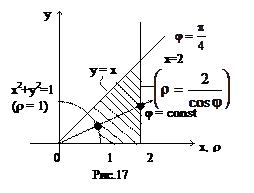
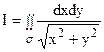
Хотя данный интеграл можно вычислить в прямоугольной декартовой системе координат, в которой он задан, но неопределенные интегралы, которые при этом возникнут, достаточно сложны.

Перейдем к полярной системе координат. Вспомним, что 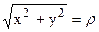. Построив область интегрирования (рис. 17), мы видим, что для точек области полярный угол меняется в пределах от 0 до p/4, а при каждом значении j из этого промежутка полярный радиус меняется от 1 до 2/cosj (последнее мы получим, подставив в уравнение х = 2 выражение для х через полярные координаты: rcosj = 2 и разрешив полученное соотношение относительно r).

Таким образом, искомый интеграл можно представить в виде:

Пример 13.

Вычислить двойной интеграл 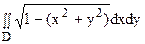, если область D ограничена окружностью x 2 + y 2 = 1.

Область D есть круг радиуса 1 с центром в начале координат. Введем полярные координаты. В полярных координатах x 2 + y 2 = r 2 и уравнение окружности принимает вид r = 1.

Тогда по формуле ( 13) получаем:

Пример 14.

Вычислить двойной интеграл 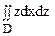, если область D ограничена половиной дуги окружности x 2 + z 2 = ax и отрезком оси Ox от точки с абсциссой равной 0 до точки с абсциссой равной а.

Область D – полукруг. Введем полярные координаты: x = rcosj, z = rsinj.

Уравнение окружности в полярных координатах принимает вид r 2 = racosj, или r = acosj.

Подынтегральная функция имеет вид z = rsinj. Угол j меняется от 0 до p/2 (полукруг находится в I четверти). При каждом фиксированном значении угла j r меняется от 0 (в начале координат) до r = acosj (на окружности). Тогда получаем:

Пример 15.

В двойном интеграле расставить пределы интегрирования в полярных координатах, если область D является квадратом с вершинами в точках О(0;0), А(1;0), В(1;1), С(0;1).

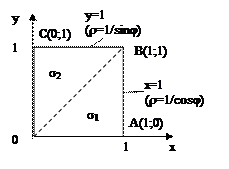
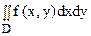
Уравнение стороны АВ (х = 1) в полярных координатах принимает вид rcosj = 1, или r = 1/cosj, а ВС будет r = 1/sinj. Угол j меняется от 0 до p/2 (квадрат находится в I четверти). При изменении угла от 0 до p/4 r меняется от 0 до r = 1/cosj, а при изменении угла от p/4 до p/2 r меняется от 0до r = 1/sinj.

Пример 16.

Вычислить двойной интеграл 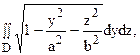если область D ограничена эллипсом

Для решения этой задачи удобно ввести так называемые обобщенные полярные координаты, положив y = arcosj, z = brsinj.

Найдем якобиан данного преобразования:

т.е. | I |= abr.

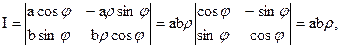
Подынтегральная функция принимает вид:

Угол j меняется от 0 до 2p. Уравнение эллипса принимает вид r = 1, поэтому r меняется от 0 до 1. И тогда

Содержание

Двойные интегралы в полярных координатах: теория и примеры
Что значит вычислить двойной интеграл в полярных координатах?
Пределы интегрирования в повторных интегралах
Случай первый
Случай второй
Случай третий
Случай четвёртый
Решения двойных интегралов в полярных координатах: примеры
Приложения двойных и тройных интегралов
Пример 3:
Координаты центра тяжести
🎥 Видео

Видео:Площадь фигуры через двойной интеграл в полярных координатахСкачать

Двойные интегралы в полярных координатах: теория и примеры

Видео:Двойной интеграл в полярных координатахСкачать

Что значит вычислить двойной интеграл в полярных координатах?

Если область интегрирования представляет собой окружность или часть окружности, двойной интеграл проще вычислить не в декартовых прямоугольных координатах, а в полярных координатах. В этом случае подынтегральная функция выражается как функция полярных переменных r и φ с использованием соотношений между полярными и декартовыми координатами x = rcosφ и y = rsinφ :

Что представляет собой элемент площади dxdy , выраженный в полярных координатах? Для ответ на этот вопрос разделим область интегрирования D на участки линиями окружности r = const и лучами φ = const . Рассмотрим один частичный участок (заштрихованный на рисунке), который ограничивают лучи, образующие с полярной осью углы φ и φ + dφ и линии окружности с радиусом r и r + dr . Этот криволинейный четырёхугольник можем приближенно считать прямоугольником с длиной боковой стороны dr и длиной основания rdφ . Поэтому элемент площади в полярных координатах выражается следующим образом:

а двойной интеграл в полярных координатах записывается так:

Чтобы вычислить двойной интеграл в полярных координатах, его нужно выразить через повторные интегралы, так же, как и «обычный» двойной интеграл в декартовых прямоугольных координатах. В полярных координатах внешний интеграл всегда интегрируется по углу φ , а внутренний — по радиусу r .

Вычислить двойной интеграл в полярных координатах — значит, как и в декартовых прямоугольных координатах, найти число, равное площади упомянутой фигуры D .

Видео:Двойной интеграл / Как находить двойной интеграл через повторный (двукратный) / Два способаСкачать

Пределы интегрирования в повторных интегралах

При переходе от двойного интеграла в полярных координатах к повторным интегралам расстановку пределов интегрирования могут облегчить следующие закономерности.

Случай первый

Полюс O является внутренней точкой области интегрирования D , область ограничена линией r = r(φ) .

Тогда соответственно нижний и верхний пределы интегрирования внешнего интеграла равны 0 и 2π , а внутреннего интеграла — 0 и r(φ) . Переход к повторным интегралам осуществляется следующим образом:

Случай второй

Полюс O находится на границе области интегрирования D , ограниченного линией r = r(φ) , но не является угловой точкой.

Через полюс O проведём касательную. Пусть касательная образует с полярной осью угол α . Тогда соответственно нижний и верхний пределы интегрирования внешнего интеграла равны α и π + α , а внутреннего интеграла — 0 и r(φ) . Переход к повторным интегралам осуществляется следующим образом:

Случай третий

Полюс O находится на границе области интегрирования D , ограниченного линией r = r(φ) , и является угловой точкой.

Из полюса O проведём лучи, которые будут ограничивать область D . Пусть эти лучи образуют с полярной осью углы α и β . Тогда соответственно нижний и верхний пределы интегрирования внешнего интеграла равны α и β , а внутреннего интеграла — 0 и r(φ) . Переход к повторным интегралам осуществляется следующим образом:

Случай четвёртый

Полюс O находится вне области интегрирования D .

Из полюса O проведём лучи, которые будут ограничивать область D . Пусть эти лучи образуют с полярной осью углы α и β , а область D ограничивают линии r = r 1 (φ) и r = r 2 (φ) . Тогда соответственно нижний и верхний пределы интегрирования внешнего интеграла равны α и β , а внутреннего интеграла — r 1 (φ) и r 2 (φ) . Переход к повторным интегралам осуществляется следующим образом:

Видео:Изменение порядка интегрирования в повторном интегралеСкачать

Решения двойных интегралов в полярных координатах: примеры

Пример 1. Вычислить в полярных координатах двойной интеграл

где область D ограничена линиями , , .

Решение. Строим на чертеже область интегрирования. Видим, что этот пример относится к третьему случаю из вышеописанных четырёх случаев расположения области интегрирования.

Выразим подынтегральную функцию как функцию полярных переменных:

Данные в условии линии, ограничивающие D , приводим к полярным координатам:

Переходим от двойного интеграла к повторному, учитывая пределы интегрирования, верные в третьем случае:

Вычисляем интеграл (так как повторные интегралы независимы друг от друга, каждый из них вычисляем отдельно и результаты перемножаем):

Пример 2. В повторном интеграле

перейти к полярной системе координат.

Решение. В повторном интеграле переменная x изменяется от -1 до 1, а переменная y — от параболы x² до 1. Таким образом, область интегрирования снизу ограничена параболой y = x² , а сверху — прямой y = 1 . Область интегирования изображена на следующем чертеже.

При переходе к полярным координатам область интегрирования нужно разделить на три части. Значит, данный повторный интеграл должен быть вычислен как сумма трёх интегралов. В первой области полярный радиус меняется от 0 до параболы, во второй области — от 0 до прямой y = 1 , в третьей области — от 0 до параболы. Точки пересечения прямой y = 1 и параболы: (1; 1) и (−1; 1) . В первой точке полярный угол составляет , во второй точке он составляет . Поэтому в первой области φ меняется от от 0 до , во второй области — от 0 до , в третьей области — от до π .

Запишем линии, ограничивающие область интегрирования в полярной системе координат. Найдём уравнение прямой y = 1 : или . Найдём уравнение параболы y = x² в полярной системе координат:

Теперь у нас есть всё, чтобы от данного повторного интеграла перейти к полярным координатам:

Пример 3. Вычислить в полярных координатах двойной интеграл

где область D ограничена линией окружности .

Решение. Строим на чертеже область интегрирования.

Область интегрирования ограничивает линия окружности с центром в точке (a; 0) и радиусом a . В этом легко убедиться, преобразовав её уравнение следующим образом:

Линия окружности касается оси Oy , поэтому полярный угол в области интегрирования меняется от до . Подставим и в уравнение окружности и получим

Напишем подынтегральную функцию в полярных координатах:

Теперь можем перейти в данном двойном интеграле к полярным координатам:

Наконец, находим двойной интеграл в полярных координатах:

В полученном выражении второе слагаемое равно нулю, так как и sinπ , и sin(−π) равны нулю. Продолжая, получаем:

Пример 4. Вычислить плоской фигуры, которую ограничивают линии , , , .

Решение. Построим заданную фигуру на следующем рисунке.

Так как фигура является частью круга, её площадь проще вычислить в полярных координатах. Данные уравнения линий перепишем в полярных координатах:

Таким образом, у нас есть всё, чтобы записать площадь фигуры в виде двойного интеграл в полярных координатах, перейти к повторному интегралу и вычислить его:

Пример 5. Вычислить в полярных координатах двойной интеграл

где область D ограничена линиями и .

Решение. Преобразуем данные уравнения линий, чтобы было проще построить чертёж:

Строим на чертеже область интегрирования.

В данных уравнениях линий перейдём к полярным координатам:

В данном двойном интеграле перейдём к полярным координатам, затем к повторным интегралам и вычислим интеграл:

Видео:Вычислить двойной интеграл по области, ограниченной линиями ∫∫(5x+y)dxdy D: y=x^3, y=0, x=3.Скачать

Приложения двойных и тройных интегралов

Содержание:

По этой ссылке вы найдёте полный курс лекций по математике:

Масса плоской фигуры Пусть задана плоская ограниченная фигура D, по которой непрерывным образом распределена масса с поверхностной плотностью — функция, непрерывная в D. Разобьем фигуру D на п частей без общих внутренних точек, площади которых соответственно равны В каждой части произвольно выберем точку У к) и вычислим в ней плотность у*).

В силу непрерывности fi(x, у) можно считать, что масса т* части Dk фигуры D приближенно равна а масса всей фигуры — сумме Приложения двойных и тройных интегралов Масса плоской фигуры Статические моменты плоской фигуры относительно осей координат Координаты центра тяжести Моменты инерции плоской фигуры относительно осей координат Статические моменты тела относительно координатных плоскостей

Центр тяжести Понятие о несобственном кратном интеграле по неограниченной области Последняя является интегральной суммой для непрерывной функции ц(х> у) в области D. Переходя к пределу при d 0 (здесь d — наибольший из диаметров частичных областей получим точное равенство Если масса распределена равномерно по всей фигуре, ц = const, то формула (1) принимает вид Пример 1.

Найти массу кольца, ограниченного двумя концентрическими окружностями радиусов г и Л, где если плотность кольца в каждой точке обратно пропорциональна расстоянию от этой точки до центра окружности и равна 1 на окружности внутреннего круга где S — площадь фигуры D.

М Фигура D задается условиями 9.2. Статические моменты плоской фигуры относительно осей координат. Координаты центра тяжести Статическим моментом Мх материальной точки массы т относительно оси Ох называется произведение ту, где у — ордината материальной точки, т. е. Здесь у может быть как положительным, так и отрицательным числом. Разбивая фигуру D на части , выбирая в каждой части Dk произвольно точку и считая, что масса этой к-й части приближенно равна и сосредоточена в точке , запишем приближенно величину статического момента фигуры D относительно оси Ох. Имеем где ASk — площадь части ) — поверхностная плотность.

Переходя к пределу при d -* 0, получаем Статический момент фигуры D относительно оси Оу находится по аналогичной формуле Если известны статические моменты Мх и Mv и масса т плоской фигуры, то координаты центра тяжести этой фигуры находятся по следующим формулам Если /1 = const, то m = /iS, где S — площадь фи гуры D, и формулы (5) принимают вид: Пример 2.

Найти центр тяжести однородн ой плоской фигуры, ограниченной косинусоидой Так как фигура — однородная, то координаты центра тяжести будем искать по фор мулам (6). Найдем сначала площадь S заданной фигуры. Имеем Затем найдем статические моменты Теперь no формулам (6) получаем Приложения двойных и тройных интегралов Масса плоской фигуры Статические моменты плоской фигуры относительно осей координат Координаты центра тяжести Моменты инерции плоской фигуры относительно осей координат Статические моменты тела относительно координатных плоскостей Центр тяжести Понятие о несобственном кратном интеграле по неограниченной области 9.3.

Моменты инерции плоской фигуры относительно осей координат Рассуждая аналогично изложенному выше, легко установить, что элементарные моменты инерции относительно осей Ох и Оу будут соответственно равны Интегрируя по плоской фигуре £>, получим формулы для самих моментов инерции где, как и ранее, — поверхностная плотность распределения масс. 9.4. Вычислен ие массы тела Рассматривая задачу, приводящую к тройному интегралу, мы показали, что если известна плотность распределения масс fi(x> у, г) в каждой точке некоторого тела ft, то масса этого тела вычисляется по формуле Мы предполагаем, что функция у, z) непрерывна в области П.

Возможно вам будут полезны данные страницы:

Пример 3:

Вычислить массу m тела, ограниченного полусферами и плоскостью хОу, если плотность в каждой точке пропорциональна расстоянию от этой тон ни до начала координат. 4 По условию задачи плотаостъ ц в точке (x,y,z) выражается формулой — коэффициент пропорциональности. Тогда Переходя к сферическим координатам, получим, что 9.5. Статические моменты тела относительно координатных плосюствв .

Центр тяжести Напомним, что задача о вычислении статических моментов и центра тяже сти плоской фигуры решалась при помощидвойных интегралов (см. формулы (3), (4) и (5)). Задачи о вычислении статических моментов тела ft относительно координатных плоскостей и отыскания центра тяжести тела ft решаются аналогичным способом при помощи тройных интегралов. Например, элементарный статический момент относительно плоскости хОу равен — плотность. Отсюда статический момент Аналогично выписываются статические моменты относительно плоскостей Вычислив массу m тела ft и его статические моменты, легко найти координаты центра тяжести тела:

Если тело однородно, то плотность = const и формулы (11) упрощаются — постоянный множитель /х в числителе можно вынести за знак интеграла и сократить на него числитель и знаменатель . Тогда получим 4. найти координаты центра тяжести Однородное о полуиира радиуса R. 4 Считаем, что центр шара находится в начале координат, а рассматриваемая фигура — полуша р расположена над плоскостью. Тогда в силу симметрии имеем Объем полушара равен Найдем статический момент относительно плосхости хОу: Значит, центр тяжести.

Понятие о несобственном кратном

интеграле по неограниченной области При необходимости интегрирования функций нескольких переменных по неограниченной области D поступают так. Выбирают последовательность ограниченных областей интегрирования , монотонно исчерпывающих область D, т. е. Например, если область интегрирования совпадает со всей плоскостью , то за последовательность можно принять совокупность концентрических кругов где Определение. Несобственным интегралом от функции /(ж, у) по неограниченной области интегрирования D называется предел последовательности интегралов не зависящий от выбора последовательности D„.

Итак, по определению (2) Если предел (1) существует и конечен, то несобственный интеграл по неограниченной области называется сходящимся, в противном случае — расходящимся. Пример 1. Вычислить интеграл где область интегрирования — вся плоскость. м В качестве областей интегрирования выберем круги радиуса п . Переходя к полярным координатам, получим Итак, интеграл (3) сходится и равен Признак сражение.

Если ,u интеграл сходится, то сходится и интеграл Если же интеграл расходится, то расходится и интеграл Интегралы, сходящиеся на всей плоскости, можно вычислять с помощью повторного интегрирования: 2. Вычислить интеграл 4 Так как то, согласно соотношению Переходя в двойном интеграле к полярным координатам, получим ноаую область интегрирования Следовательно, откуда Несобственные интегралы от функции трех, четырех и большего числа переменных по неограниченным областям определяются аналогично. Упражнения Вычислите двойные интегралы:

Измените порядок интегрирования (предварительно нарисовав область интегрирования): Нарисуйте область интегрирования и вычислите повторные интегралы Вычислите площади фигур, ограниченных кривыми Вычислите площадь петли кривой Вычислите площадь петли кривой Указание. Сделайте замену переменных Пугем перехода к полярным координатам вычислите следующие интегралы: если область D ограничена окружностью с центром в начале координат. — кольцо между окружностями радиусов полукруг диаметра d с центром в точке С о) , лежащий выше Приложения двойных и тройных интегралов Масса плоской фигуры Статические моменты плоской фигуры относительно осей координат

Координаты центра тяжести

Моменты инерции плоской фигуры относительно осей координат Статические моменты тела относительно координатных плоскостей Центр тяжести Понятие о несобственном кратном интеграле по неограниченной области Найдите массу штастиики D с заданной поверхностной плотностью Определите центры тяжести: 31. Полусегмента параболы 32. Полуэллипса отсеченного осью Ох. 33. Фигуры, ограниченной кривыми Вычислите площадь: 34.

Той части плоскости , которая лежит в первом октанте и ограничена цилиндром 35. Той части поверхности конусах которая высекается цилиндром 36. Поверхности параболоида расположенного внутри цилиндра . Вычислите интегралы по площади поверхности: 3часть плоскости , лежащая в первом октанте. где ж — часть сферы лежащая в первом октанте. — цилиндр х ограниченный плоскостями расстояние от точки ) поверхности до начала координат. Определение. Моментом инерции плоской фигуры относительно начала координат называется величина ‘ Вычислите моменты инерции относительно начала координат: 40.

Треугольника, ограниченного линиями , относительно оси Ох. 41. Треугольника с вершинами в точках относительно оси Оу. 42. Эллипса относительно оси Оу. 43. Области, ограниченной параболой у2 = 4ах, прямой Вычислите тройные интегралы: — область, ограниченная координатными плоскостями и плоскостью где ft — область, ограниченная конусом и плоско- — трехгранная призма, ограниченная плоскостя- п ми Вычислите инте1ралы 47-50, переходя к цилиндрическим или сферическим координатам: I

Вычислите объем тела, огранич енного данными поверхностями: . Указание: перейдюе к сферическим координатам. Вычислите массу тела: 54. Ограниченного поверхностями , «ели плогность ц в каждой точке тела равна аппликате этой точке. 55. Ограниченного поверхностями , если плотность/х в каждой точке равна орданате у этой точки.

Найдете статические моменты однородного тела (ц = 1): 56. Прямоугольного параллелепипеда с ребра*» а, Ь,с, относительно его граней. 57. Тела, ограниченного эллипсоидом х2 у2 z2 и плоскостью хОу, относительно плоскости хОу. Найдите координаты центра тяжести однородного тела (/* = 1), ограниченного данными поверхностями: 58. Плоскостями 59. Цилиндром и плоскостями 60. Параболоидом х2 + у2 = 2л z и полусферой .

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.