Предположим, мы опоясали земной шар по экватору прочной веревкой. Для упрощения считаем, что Земля является идеальной сферой с длиной экватора 40 тыс. км.
Затем мы хотим поднять веревку на высоту 1 метра от земли по всей окружности экватора. Имейте в виду, что веревка идет по всему миру, от Африки через Атлантику до Бразилии, сквозь Эквадор, через Тихий океан, до индонезийских островов, через Сингапур и Суматру, через Индийский океан снова до Африки. Так что если мы поднимем ее на высоту 1 метра, нам потребуется существенно увеличить ее длину, не так ли?
Хорошо, давайте решим эту задачу, используя простую школьную математику. Вы помните из геометрии 6-го класса, что длина окружности задается формулой
С = 2πR
где C— длина окружности, а R – ее радиус.
Итак, чтобы найти увеличение длины веревки, мы просто берем длину веревки, когда она находится в 1 метре над землей, и вычитаем из нее длину веревки на земле. Разница в метрах между длинами веревок 2π(R+1) и 2πR равна всего лишь 2π, или 6 метров 28 сантиметров.
Интересно отметить, что ответ не зависит от размера Земли, а только от расстояния, на котором веревка находится над землей. Другими словами, знание длины окружности Земли не имеет значения. Это означает, что если вы натянете веревку вокруг апельсина (или вокруг Солнца), а потом сместите ее на 1 метр, увеличение длины веревки все равно будет таким же. Увеличение радиуса окружности на одну единицу дает увеличение длины окружности на 2π единиц.
Эту задачу можно сформулировать и обратным способом. Пусть у вас есть веревка, лежащая на земле вокруг экватора, и если вы как-то добавили 1 метр к длине веревки и аккуратно расправили ее в виде окружности с центром в центре Земли, поднимется ли веревка на достаточное расстояние, чтобы под ней мог проползти муравей? Рассчитайте эту величину самостоятельно.
А что получится, если экватор объекта вместо круглой формы (Земля, Солнце, апельсин) имеет квадратную форму? Треугольную форму?
Логические задачи и головоломки
Предположим, что земной шар по экватору плотно обтянут веревкой. Длину веревки увеличили на 1м. Образовавшийся зазор равномерно распределен по экватору. Сможет ли в этот зазор прошмыгнуть мышь?
Ответ: Расстояние между двумя концентрическими окружностями, если длина одной больше длины другой на 1 метр, равно 1/(2Пи) метров > 15см и не зависит от радиусов окружностей. Т.е. мышь прошмыгнуть сможет.
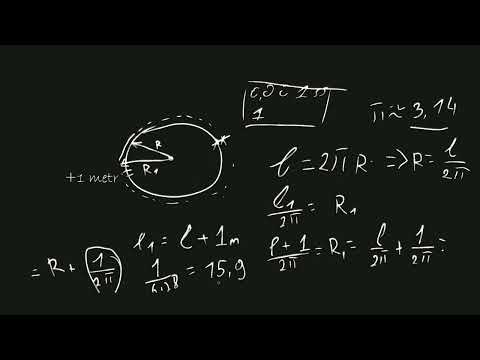
Комментарии
Оставлен Андрей Ср, 05/26/2010 — 10:35
Оставлен Гость Чт, 06/24/2010 — 17:28
ПОПОДРОБНЕЙ
ответ правильный
L1=2Pi*R1 где R1 радиус веревки равный радиусу земли
L2=2Pi*R2 где R2 радиус веревки равный радиусу земли + 1 м
L2-L1=1 m = 2Pi*(R2-R1)
R2= (1/2(Pi))+ R1
т.е. не зависимо от радиуса окружностей добавка доваемая по длине на 1 м. дает увеличение радиуса на 1/(2Pi)=0,159 м (около 16 сантиметров)
Оставлен Гость Пнд, 01/10/2011 — 02:12
Да помоему там ничто не пролезет, длинна оружности Земли гигантсткая, плюс 1м к этой веревке и опять растянуть равномерно. У меня вообще мнение что натяжение веревки лишь слегка упадет )))
Оставлен катенька Пт, 01/21/2011 — 13:10
Мышь может поднырнуть под верёвку. И увеличивать ничего не нужно.
Оставлен Гость Пт, 05/27/2011 — 10:39
Смотря какая веревка. Если слишком тонкая как нитка, то мышь не сможет. И наоборот, если веревка очень толстая и тяжелая, то мышь тоже не сможет поднять веревку.
Оставлен Гость Пт, 09/30/2011 — 12:26
да мышь эту веревку перегрызет и все)
Оставлен Одіс Пнд, 02/06/2012 — 14:22
Да друзі.. це містика, або математична помилка, але це дійсний факт.. спробуйте дійсно підставити різні величини і побачите що результат без змін. 0,1592 метра зміна радіуса завжди, при добавленні до довжини кола +1. Пов’язане з самим числом П, через яке ми вираховуємо довжину кола. Пі буквально це довжина поділена на діаметр або іншими словами довжина на 2 радіуса.якщо скажімо довжина 1 то діаметр буде 1 / 3,14*2 = 1 / 6,28= 0,1592. інше питання що формула передбачає операції з додаванням, а не множенням, а за таких умов сталий результат є дивним, оскільки не йде мова про відсоткове збільшення радіуса залежно від довжини кола, йде мова про буквальне збільшення радіуса на сталу величину.. цікава річ, варта дослідження
math4school.ru
Земля и апельсин
Задача, которая будет рассмотрена ниже, – весьма проста и понимание её решения не требует сколько-нибудь серьёзного уровня математической подготовки. И, тем не менее, присутствие этой задачи в разделе Магия математики , весьма оправдано, потому что парадоксальность вывода, к которому мы придём, и его упорное несоответствие здравому смыслу на первый взгляд просто удивительны.
Итак, вообразим, что земной шар обтянут по экватору обручем, и подобным же образом обтянут апельсин по его большому кругу. Далее вообразим, что окружность каждого обруча удлинилась на 1 метр. Тогда, разумеется, обручи отстанут от поверхностей тел, которые они раньше стягивали, и образуется некоторый зазор. Спрашивается, в каком случае этот зазор будет больше – у земного шара или у апельсина?
Здравый смысл подсказывает такой ответ: «Конечно, у апельсина образуется больший зазор, чем у Земли! Ведь в сравнении с длиной экватора земного шара – более 40 000 км – какой-нибудь один метр есть столь ничтожная величина, что прибавка её останется совершенно незаметной. Другое дело апельсин: по сравнению с его окружностью один метр – весьма существенная величина, и прибавка её к длине окружности, конечно, должна быть ощутима».
Однако давайте проверим этот вывод с помощью несложных вычислений. Пусть длина окружности земного шара равна L , а апельсина l метрам. Тогда радиус Земли и радиус апельсина равны соответственно:
| R = | L | и | r = | l |
| 2 π | 2 π |
После прибавки к обручам одного метра окружность обруча у Земли будет (L + 1) , а у апельсина (l + 1) , новые радиусы же R’ и r’ будут равны
| R’ = | L + 1 | и | r’ = | l + 1 |
| 2 π | 2 π |
Если из новых радиусов вычтем прежние, то получим в обоих случаях одно и то же их изменение:
| R’ – R = | L + 1 | – | L | = | 1 | – для земного шара, |
| 2 π | 2 π | 2 π |
| r’ – r = | l + 1 | – | l | = | 1 | – для апельсина. |
| 2 π | 2 π | 2 π |
Итак, и у Земли, и у апельсина получится один и тот же зазор в 1/2 π метра, что чуть меньше 16 сантиметров. «Просто и удивительно! Вот уж действительно – магия,» – восторженно воскликнет зритель.
А между тем, мы столкнулись с фактом, вытекающим из постоянства отношения длины окружности к её радиусу. Эффект же этой задачи объясняется отношением абсолютной величины зазора в 16 см к размерам апельсина и размерам земного шара. В первом случае – это весьма заметно, во втором – ничтожно мало. Если же взять бесконечно малый шар (точку), радиус и длина большой окружности которого равны нулю, то радиус увеличенного обруча будет равен величине установившегося зазора в 1/2 π метра, что бесконечно больше чем ноль. Так что обвинять здравый смысл в полном отсутствии здравости всё же нельзя.