Если две точки окружности лежат в некоторой плоскости то (7 видео)

8. Верно ли утверждение: а) если две точки окружности лежат в плоскости, то и вся окружность лежит в этой плоскости; б) если три точки окружности лежат в плоскости, то и вся окружность лежит в этой плоскости?

а) Неверно. Пример:

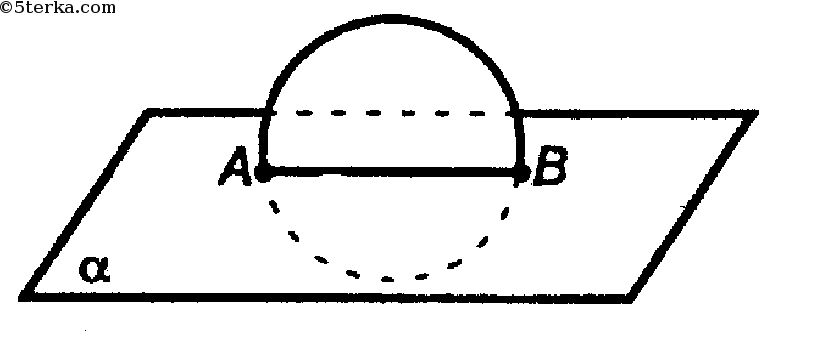
А ∈ α, В ∈ α. Но окружность пересекает а и не лежит в ней.

б) Верно, так как три точки однозначно задают окружность, поэтому все ее точки будут лежать в заданной плоскости.

Ответ: а) нет; б) да.

Решебник по геометрии за 10 класс (Л.С.Атанасян, 2001 год),
задача №8
к главе «Введение».

Видео:10 класс, 3 урок, Некоторые следствия из аксиомСкачать

Всё про окружность и круг

Окружность — это геометрическое место точек плоскости, равноудаленных от некоторой заданной точки (центра окружности). Расстояние между любой точкой окружности и ее центром называется радиусом окружности (радиус обозначают буквой R).
Значит, окружность — это линия на плоскости, каждая точка которой расположена на одинаковом расстоянии от центра окружности.

Кругом называется часть плоскости, ограниченная окружностью и включающая ее центр.

Отрезок, соединяющий две точки окружности, называется хордой. Хорда, проходящая через центр окружности, представляет собой диаметр. Диаметр окружности равен ее удвоенному радиусу: D = 2R.

Точка пересечения двух хорд делит каждую хорду на отрезки, произведение которых одинаково: a1a2 = b1b2

Касательная к окружности всегда перпендикулярна радиусу, проведенному в точку касания.

Отрезки касательных к окружности, проведенные из одной точки, равны: AB = AC, центр окружности лежит на биссектрисе угла BAC.

Квадрат касательной равен произведению секущей на ее внешнюю часть

Центральный угол — это угол, вершина которого совпадает с центром окружности.

Дугой называется часть окружности, заключенная между двумя точками.

Мерой дуги (в градусах или радианах) является центральный угол, опирающийся на данную дугу.

Вписанный угол это угол, вершина которого лежит на окружности, а cтороны угла пересекают ее.

Вписанный угол равен половине центрального, если оба угла опираются на одну и ту же дугу окружности.
Внутренние углы, опирающиеся на одну и ту же дугу, равны.

Сектором круга называется геометрическая фигура, ограниченная двумя радиусами и дугой, на которую опираются данные радиусы.

Периметр сектора: P = s + 2R.

Площадь сектора: S = Rs/2 = ПR 2 а/360°.

Сегментом круга называется геометрическая фигура, ограниченная хордой и стягиваемой ею дугой.

Видео:Задание №8 — ГДЗ по геометрии 10 класс (Атанасян Л.С.)Скачать

Презентация «Некоторые следствия из аксиом»

Документы в архиве:

Название документа 3.

Описание презентации по отдельным слайдам:

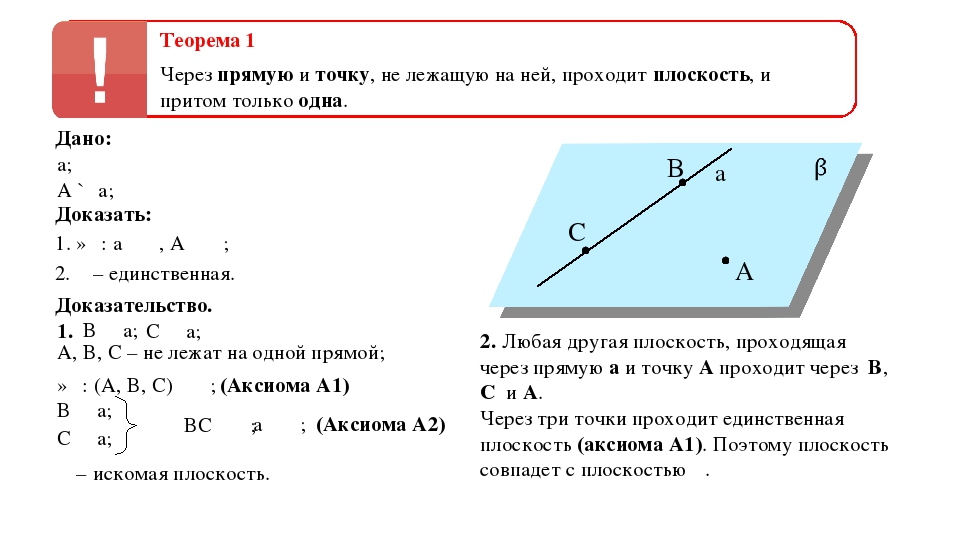
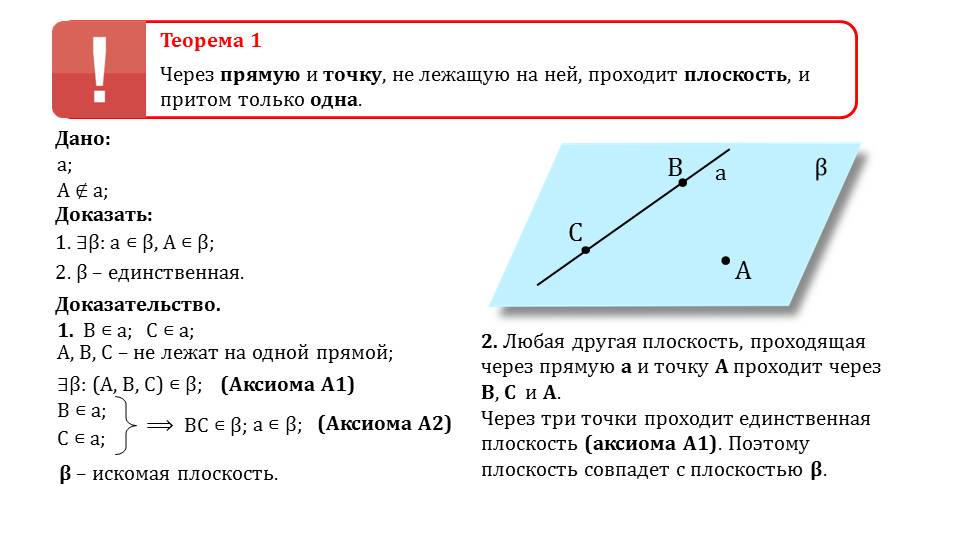
Теорема 1 Через прямую и точку, не лежащую на ней, проходит плоскость, и притом только одна. a Дано: a; A ∉ a; Доказать: 1. ∃β: a ∊ β, A ∊ β; 2. β – единственная. Доказательство. 1. B ∊ a; C ∊ a; ∃β: (A, B, C) ∊ β; A, B, C – не лежат на одной прямой; (Аксиома А1) B ∊ a; C ∊ a; ⟹ BC ∊ β; a ∊ β; (Аксиома А2) β – искомая плоскость. 2. Любая другая плоскость, проходящая через прямую a и точку A проходит через B, C и A. Через три точки проходит единственная плоскость (аксиома А1). Поэтому плоскость совпадет с плоскостью β.

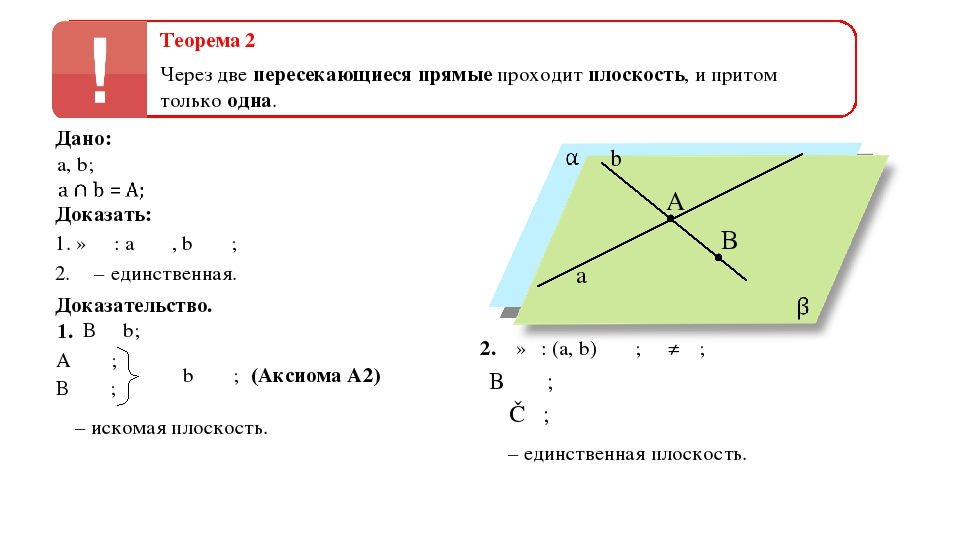
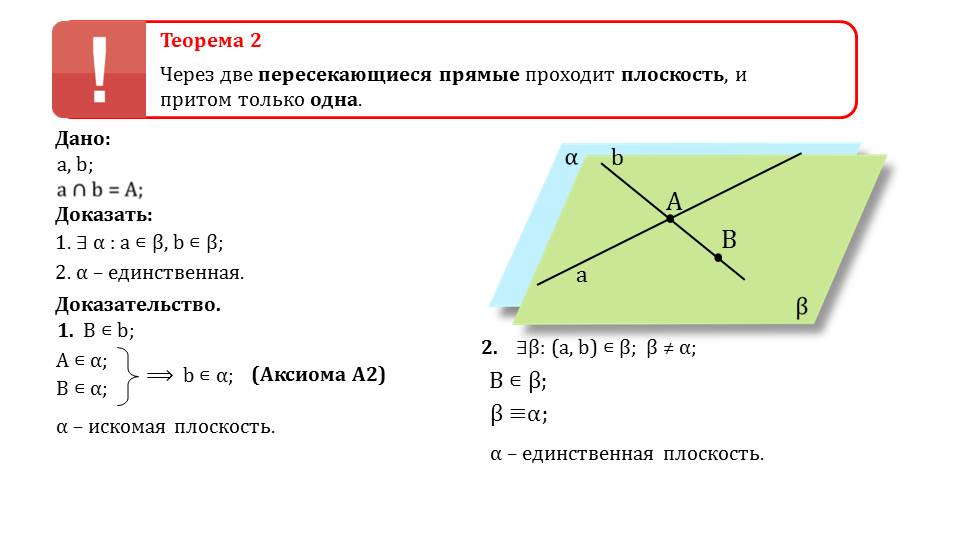
Теорема 2 Через две пересекающиеся прямые проходит плоскость, и притом только одна. Дано: a, b; Доказать: 1. ∃ α : a ∊ β, b ∊ β; 2. α – единственная. Доказательство. 1. B ∊ b; ∃β: (a, b) ∊ β; β ≠ α; A ∊ α; B ∊ α; ⟹ b ∊ α; (Аксиома А2) α – искомая плоскость. 2. a b B ∊ β; β ≡α; α – единственная плоскость.

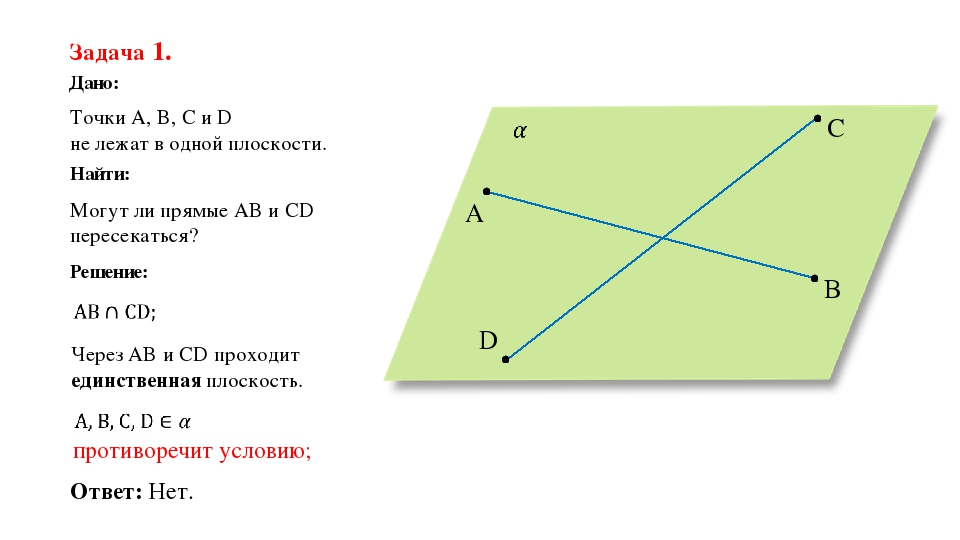
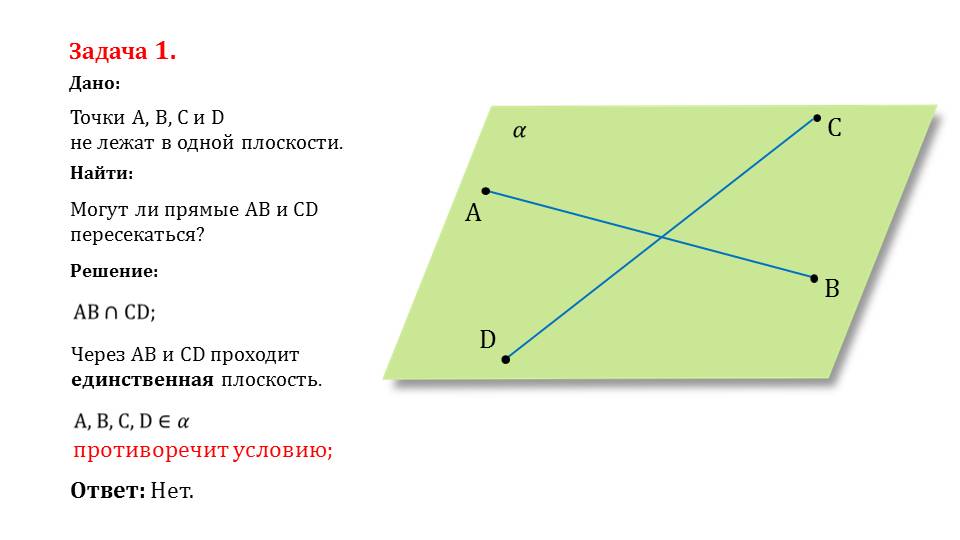
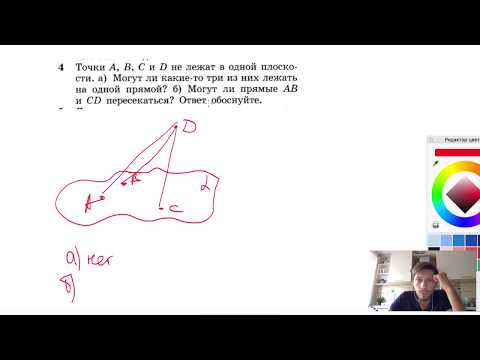
Могут ли прямые AB и CD пересекаться? Задача 1. Дано: Точки A, B, C и D не лежат в одной плоскости. Найти: Решение: Через AB и CD проходит единственная плоскость. противоречит условию; Ответ: Нет.

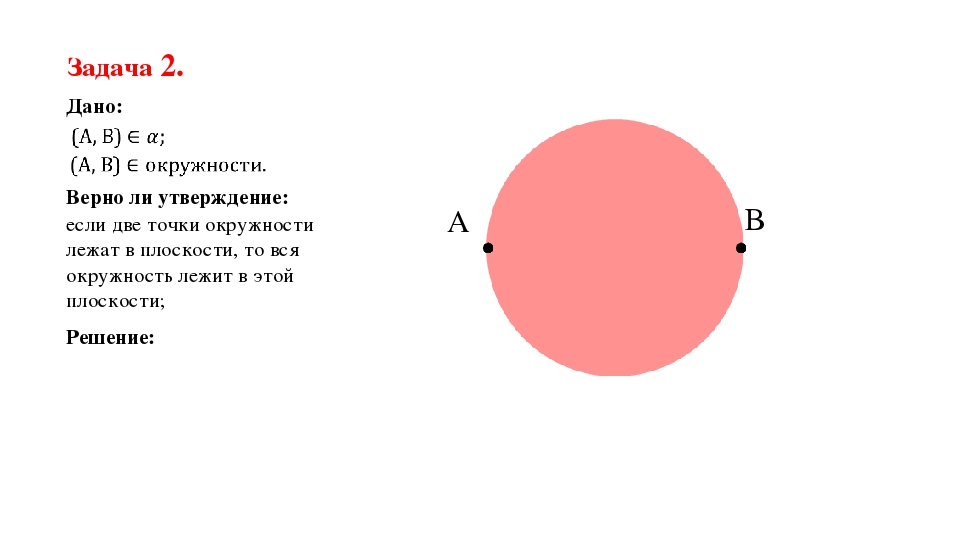
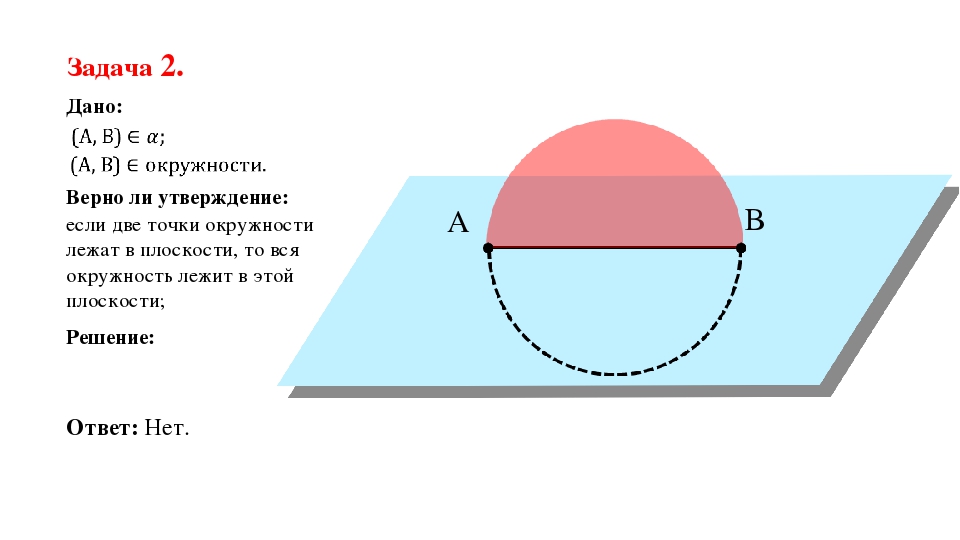
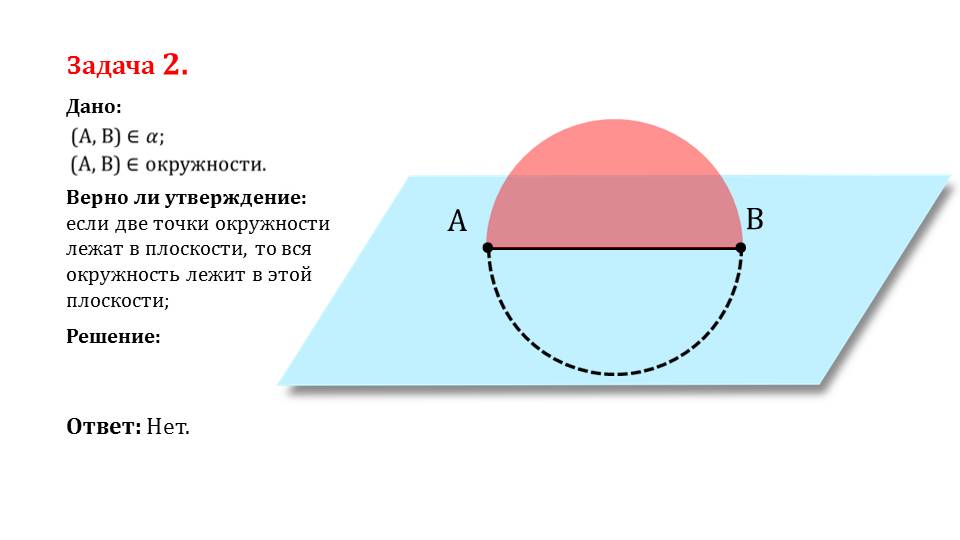
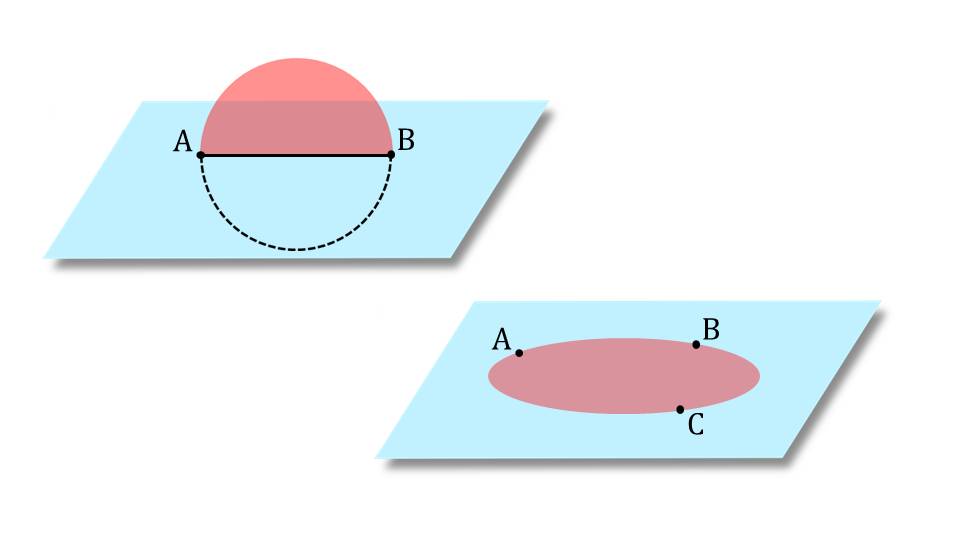
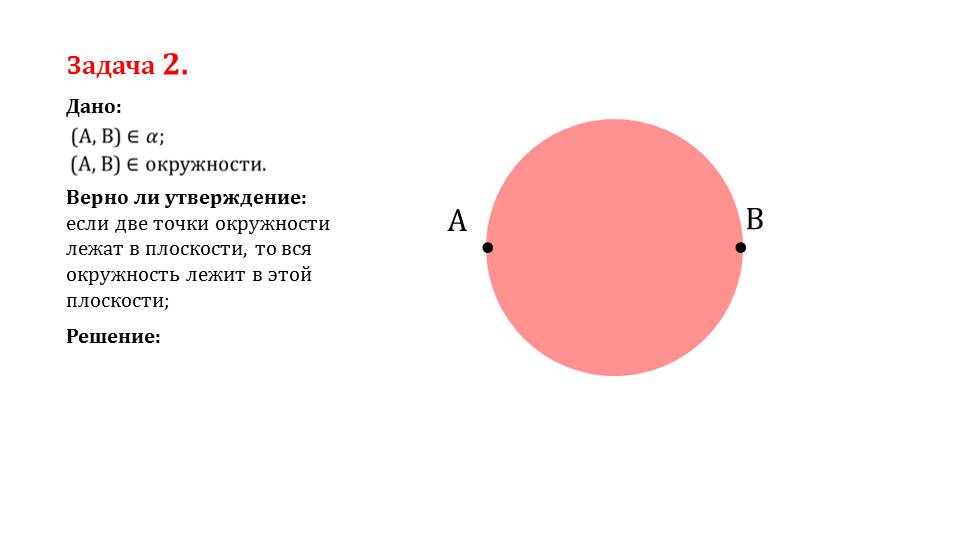
если две точки окружности лежат в плоскости, то вся окружность лежит в этой плоскости; Задача 2. Дано: Верно ли утверждение: Решение:

если две точки окружности лежат в плоскости, то вся окружность лежит в этой плоскости; Задача 2. Дано: Верно ли утверждение: Решение: Ответ: Нет.

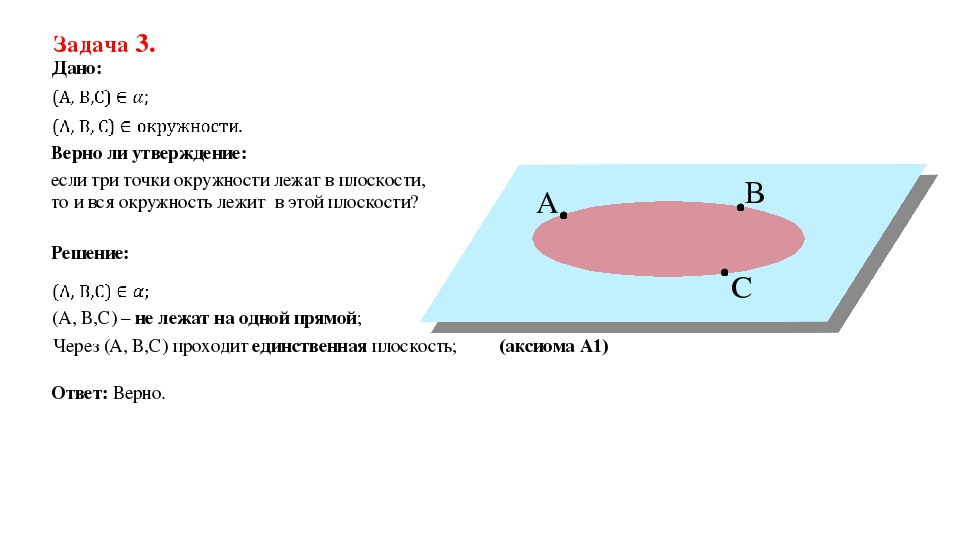
если три точки окружности лежат в плоскости, то и вся окружность лежит в этой плоскости? Задача 3. Дано: Верно ли утверждение: Решение: (A, B,C) – не лежат на одной прямой; Через (A, B,C) проходит единственная плоскость; (аксиома A1) Ответ: Верно.

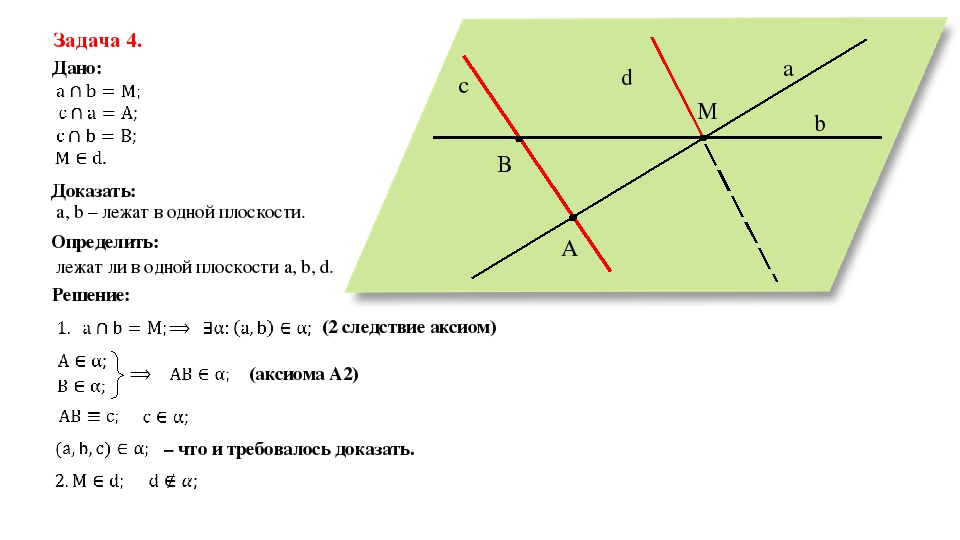
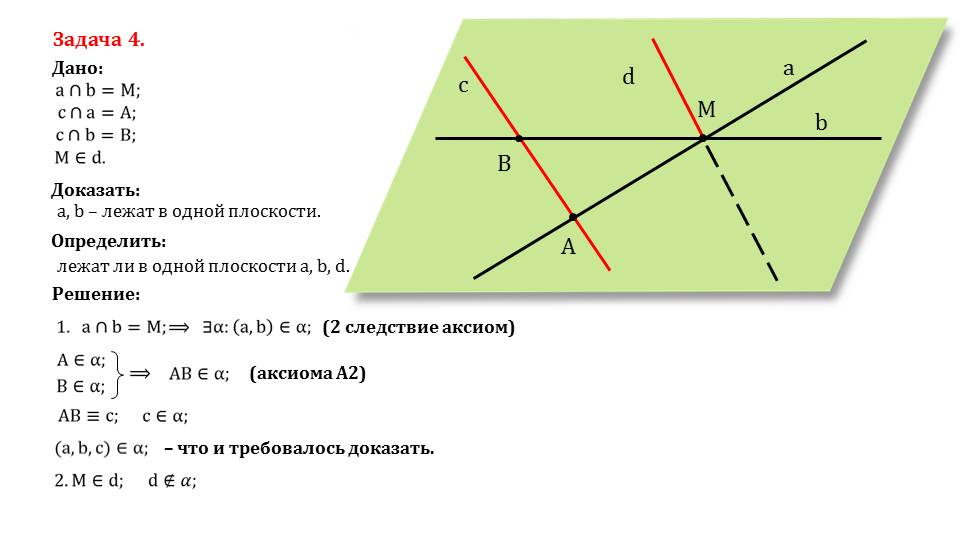
Задача 4. Дано: Доказать: Решение: a, b – лежат в одной плоскости. Определить: лежат ли в одной плоскости a, b, d. (2 следствие аксиом) (аксиома А2) – что и требовалось доказать. a b M c d B A

Краткое описание документа:

Презентация «Некоторые следствия из аксиом» является отличным обучающим материалом для учеников в 10 классе. Она является логическим продолжением предыдущего урока, который полностью раскрывал тему «Аксиомы в стереометрии». От изученных аксиом следуют некоторые утверждения и признаки, которые стоит также изучить. Они помогут при решении некоторых задач. Понять из необходимо.

Стереометрия содержит в себе огромное количество теорем, при доказательстве которых важную роль играют знания об аксиомах. Без этих знаний доказать теоремы будет невозможно.

Данная презентация посвящена рассмотрению формулировок и доказательств некоторых важных теорем, которые необходимы для решения задач в стереометрии. Прежде чем начать проведение данного урока, стоит напомнить ученикам основные аксиомы, либо потребовать, чтобы они самостоятельно их воспроизвели.

10-классники должны научиться разобраться в теоремах в стереометрии и понимать их доказательства. Также они должны уметь воспроизводить их и правильно использовать.

Первая теорема сулит о том, что через одну прямую и точку, которая не принадлежит ей, можно провести лишь одну плоскость. Формулировка и доказательство данной теоремы приводится на этом слайде. Они грамотно сформулированы и эстетично оформлены. Доказательство приведено в 2 пункта. В ней приводятся ссылки на первую и вторую аксиомы. Есть также иллюстрация, на которой видим суть теорему в геометрическом смысле. Благодаря им доказательство становится более наглядной.

Вторая теорема, которая начинается рассматриваться со второго слайда. Гласит о том, что через две пересекающиеся произвольные прямые можно провести лишь одну некоторую плоскость. Для того, чтобы доказать данную теорему, необходимо вспомнить вторую аксиому.

Первая задача, которая приводится в презентации, предлагает ответить на вопрос, могут ли 4 точки, которые не лежат на одной плоскости, составить две пересекающиеся прямые. Задача проиллюстрирована на следующем слайде наглядным образом. При доказательстве ответа на данную задачу применяется метод «от противного».

Вторая задача предлагает ответить на интересный вопрос. Если известно, что две точки, лежащие на некоторой окружности, лежат в плоскости, то лежит ли окружность также не плоскости? Задача очень интересна, ее можно предоставить школьникам для самостоятельного разбора. Приведена иллюстрация к задаче, для того, чтобы школьники могли пространственно это представить.

Ответ является «нет». Дело в том, что двух точек недостаточно, чтобы черед них проходила лишь одна плоскость. Для этого необходимо, чтобы были, как минимум, три точки, согласно рассмотренной ранее теореме. Таким образом окружность вовсе не обязана лежать на такой же плоскости, которая проходит через прямую, проведенную через две заданные точки на ней.

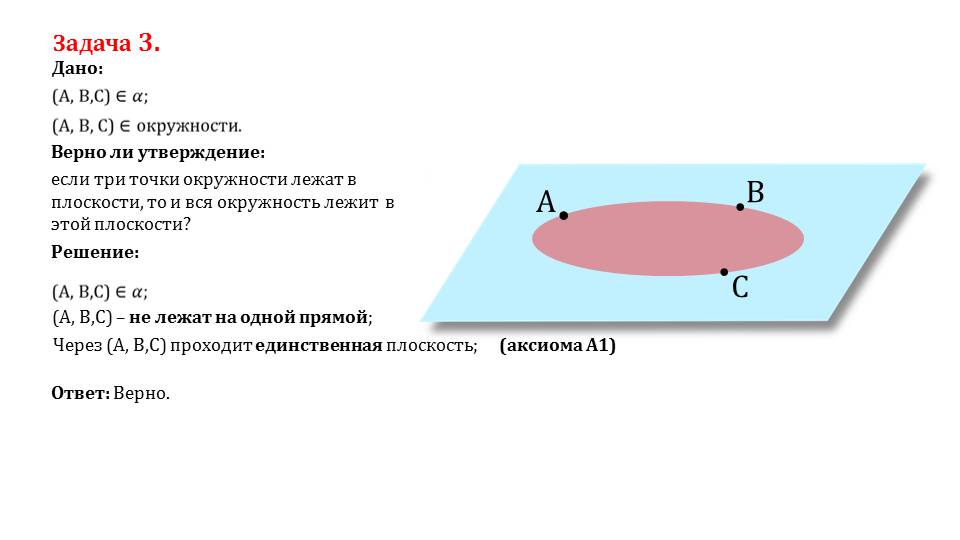
А следующая задача является аналогичной предыдущей. Отличается тем, что заданы три точки на некоторой плоскости, которые лежат на окружности. В этом случае, ответ на задачу является «да». При ее решении ссылаемся на первую аксиому.

Четвертая задача является более сложной. Ее лучше рассмотреть вместе с учителем во время урока. При ее решении используется вторая аксиома и следствие из нее.