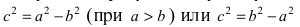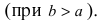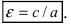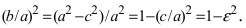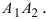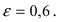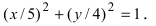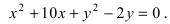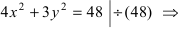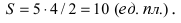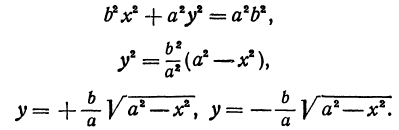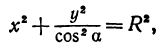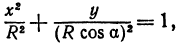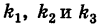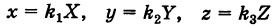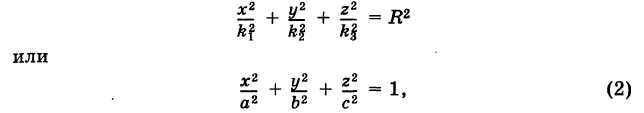Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

We are checking your browser. gufo.me
Видео:§28 Эксцентриситет эллипсаСкачать

Why do I have to complete a CAPTCHA?
Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

What can I do to prevent this in the future?
If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.
If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.
Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store.
Cloudflare Ray ID: 6d218e1cad9c8fd3 • Your IP : 85.95.179.65 • Performance & security by Cloudflare
Видео:ЭллипсСкачать

# Эксцентриситет
Эксцентриситет (в математике) — числовая характеристика конического сечения, характеризующая степень его отклонения от окружности. Окружность имеет нулевой эксцентриситет, эксцентриситет величиной менее единицы присущ эллипсам, равный единице — параболе, более единицы — гиперболе.
Согласно первому закону Кеплера, орбиты планет представляют собой эллипсы с Солнцем в одном из их полюсов. Поскольку эллипс есть частный случай конического сечения, то к орбитам планет тоже применимо понятие эксцентриситета. В данном случае он говорит о степени сжатости орбит.
Орбиты планет Солнечной системы имеют, как правило, невысокий эксцентриситет. Самый низкий эксцентриситет у орбиты Венеры (0,007), самый высокий — у орбиты Меркурия (0,205). Он стал чемпионом по планетному эксцентриситету после того, как Плутон с его эксцентриситетом 0,244 переквалифицировали в карликовые планеты. Эксцентриситет Марса — 0,093, что делает его орбиту одной из самых эксцентричных в Солнечной системе после Меркурия. Любопытно, что в течение долгого времени орбита Марса становилась более эксцентричной. Эксцентриситет земной орбиты равен 0,017, так что она довольно близка к окружности. У некоторых астероидов и комет орбиты очень вытянуты, их эксцентриситеты мало отличаются от единицы.
В технике существует понятие эксцентриситета, совершенно отличающееся от математического понятия. Оно относится к эксцентрикам — цилиндрическим валам со смещенной осью вращения. В этом случае эксцентриситетом называется расстояние между осью вращения и осью вала.
Видео:Длина окружности. Площадь круга. 6 класс.Скачать

Эллипс — определение и вычисление с примерами решения
Эллипс:
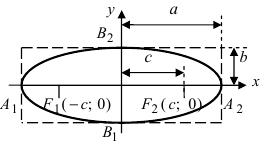
Определение: Эллипсом называется геометрическое место точек, сумма расстояний от которых до двух выделенных точек
Получим каноническое уравнение эллипса. Выберем декартову систему координат так, чтобы фокусы
Рис. 29. Вывод уравнения эллипса.
Расстояние между фокусами (фокусное расстояние) равно 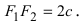
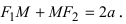
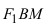
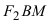
соответственно. Следовательно, согласно определению имеем
Возведем обе части равенства в квадрат, получим
Перенося квадратный корень в левую часть, а все остальное в правую часть равенства, находим 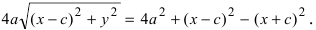
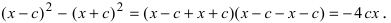
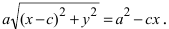
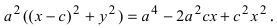
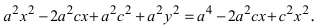
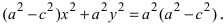
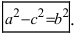
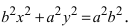
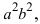
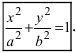
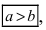
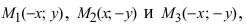
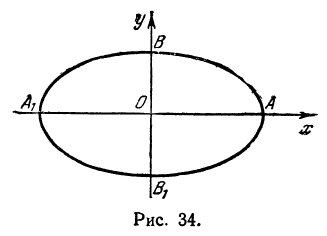
т.е. точками пересечения эллипса с осью абсцисс будут точки
т.е. точками пересечения эллипса с осью ординат будут точки
(Рис. 30).
Определение: Найденные точки называются вершинами эллипса.
Рис. 30. Вершины, фокусы и параметры эллипса
Определение: Если 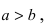
Определение: Эксцентриситетом эллипса называется отношение фокусного рас- стояния к большой полуоси эллипса
Из определения эксцентриситета эллипса следует, что он удовлетворяет двойному неравенству 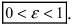
Если 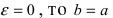
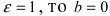
Пример:
Составить уравнение эллипса, если его большая полуось а = 5, а его эксцентриситет
Решение:
Исходя из понятия эксцентриситета, найдем абсциссу фокуса, т.е. параметр 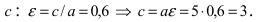
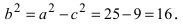
Пример:
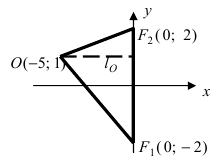
Найти площадь треугольника, две вершины которого находятся в фокусах эллипса 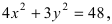
Решение:
Для определения координат фокусов эллипса и центра окружности преобразуем их уравнения к каноническому виду. Эллипс:
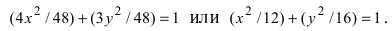
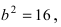
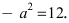
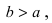
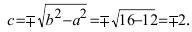
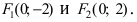
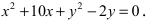
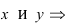
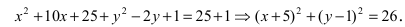
Построим в декартовой системе координат треугольник 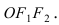
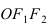
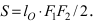
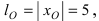
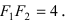
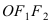
Видео:165. Найти фокусы и эксцентриситет эллипса.Скачать

Эллипс в высшей математике
где 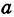
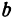
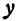
Отсюда видно, что уравнение (2) определяет две функции. Пока независимое переменное 
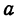

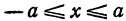
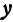
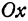
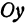
При 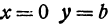
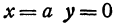
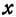

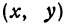
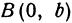
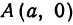
Полученная линия называется эллипсом. Число 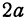
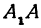
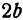
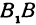
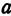
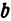
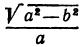
Пример:
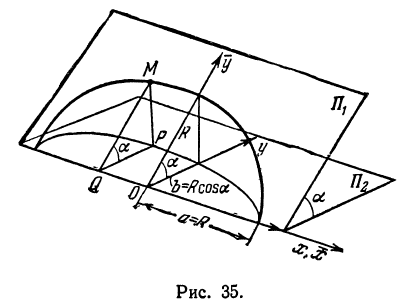
Найти проекцию окружности на плоскость, не совпадающую с плоскостью окружности.
Решение:
Возьмем две плоскости, пересекающиеся под углом 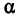
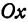
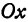
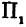
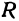
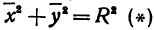
Пусть точка 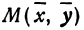
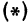
Обозначим проекцию точки 
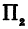
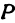
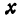
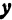


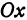
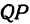
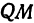
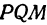
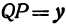
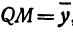
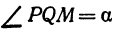
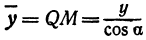


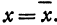
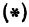
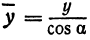
а это есть уравнение эллипса с полуосями 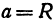
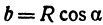
Таким образом, эллипс является проекцией окружности на плоскость, расположенную под углом к плоскости окружности.
Замечание. Окружность можно рассматривать как эллипс с равными полуосями.
Видео:#207. Окружность девяти точек | лемма о трезубце | ортотреугольник | прямая ЭйлераСкачать

Уравнение эллипсоида
Определение: Трехосным эллипсоидом называется поверхность, полученная в результате равномерной деформации (растяжения или сжатия) сферы по трем взаимно перпендикулярным направлениям.
Рассмотрим сферу радиуса R с центром в начале координат:
где Х, У, Z — текущие координаты точки сферы.
Пусть данная сфера подвергнута равномерной деформации в направлении координатных осей 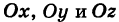
В результате сфера превратится в эллипсоид, а точка сферы М (X, У, Z) с текущими координатами Х, У, Z перейдет в точку эллипсоидам 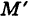
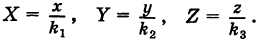
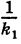
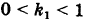
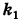
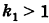
Подставляя эти формулы в уравнение (1), будем иметь
где 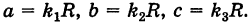
Величины 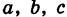
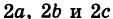
Если две полуоси эллипсоида равны между собой, то эллипсоид называется эллипсоидом вращения, так как может быть получен в результате вращения эллипса вокруг одной из его осей. Например, в геодезии считают поверхность земного шара эллипсоидом вращения с полуосями
а = b = 6377 км и с = 6356 км.
Если а = b = с, то эллипсоид превращается в сферу.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Гипербола
- Парабола
- Многогранник
- Решение задач на вычисление площадей
- Шар в геометрии
- Правильные многогранники в геометрии
- Многогранники
- Окружность
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
🎦 Видео
Аналитическая геометрия: окружность и эллипсСкачать
Урок 16: Эксцентриситет и директрисы (теория)Скачать

Аналитическая геометрия, 7 урок, Линии второго порядкаСкачать

Задача 6 №27859 ЕГЭ по математике. Урок 104Скачать

Аналитическая геометрия: Эллипс, Парабола, Гипербола. Высшая математикаСкачать

Найти центр и радиус окружностиСкачать

§29 Эксцентриситет гиперболыСкачать

Все об окружностях на ЕГЭ | Профильная математика 2023 | УмскулСкачать

Лекция 31.1. Кривые второго порядка. ЭллипсСкачать

§31.1 Приведение уравнения кривой к каноническому видуСкачать

Эллипс. Определение. Уравнение. График. Фокусы. Главные оси. Эксцентриситет - Новиков АлександрСкачать

Законы КеплераСкачать

Видеоурок "Гипербола"Скачать

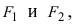
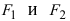
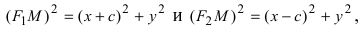
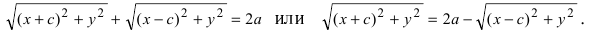
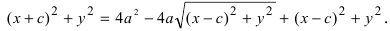
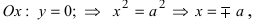 т.е. точками пересечения эллипса с осью абсцисс будут точки
т.е. точками пересечения эллипса с осью абсцисс будут точки 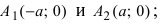
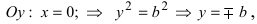 т.е. точками пересечения эллипса с осью ординат будут точки
т.е. точками пересечения эллипса с осью ординат будут точки 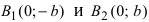 (Рис. 30).
(Рис. 30).