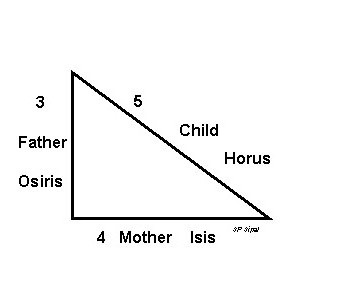
Египетский треугольник высота к гипотенузе

Египетский треугольник – прямоугольный треугольник с отношением сторон 3:4:5. Это наиболее простой из треугольников, стороны и площади которых выражаются целыми числами. Он представляет собой прекрасную иллюстрацию теоремы Пифагора – действительно, квадрат его гипотенузы (25) очевидно равен сумме квадратов его катетов (9 и 16). Предполагается даже, что именно знакомство с египетским треугольником сподвигло Пифагора на формулировку его теоремы. Впрочем, как всегда в подобных случаях, историки древности, которые не являются специалистами ни в одной другой области знания, кроме истории (и уж точно плохо смыслят в математике), могут ошибаться.

Так или иначе, имеются многочисленные указания на то, что теорема Пифагора вообще и египетский треугольник в частности были известны и широко использовались за много веков до Пифагора и далеко за пределами Египта – в Месопотамии, в долине Инда, в древнем Китае. И вправду, корень многих знаний следует искать, наверное, в практической деятельности человека. Как только возникла необходимость возводить здания и сооружения, человек эмпирическим путём пришёл к пониманию важности прямых углов. А как отмерить прямой угол, не имея геодезических приборов?

Оказывается, очень просто. Берём верёвку и делим её на 12 равных частей – например, при помощи складывания. Выбираем отрезок верёвки, равный 5, так, чтобы он находился межды двумя другими, равными 3 и 4. Выпрямляем его и фиксируем на ровном участке земли при помощи двух колышков. А затем натягиваем концы верёвки и сводим их в одну точку, чтобы получился треугольник. Прямоугольный, египетский.

«Делай, как делается». Знаменитая древнеегипетская пословица, дошедшая до наших дней. У нас её обычно понимают, как мудрое наблюдение: если так получается, значит, так правильно. Но при этом часто забывают культурно-исторический контекст Древнего Египта. Всеми работами руководили жрецы – члены замкнутой касты харнителей священного, древнего знания. Поэтому «делай, как делается» в древнеегипетском контексте наверняка значило «делай как говорят и не задавай лишних вопросов». То есть жрецы знали не только, «как» делать, чтобы «делалось», но и «почему», и это зание было скрыто от непосвящённых.

Мы тоже хотим знать, «почему». Нам недостаточно «как». Человеческий ум будоражат разнообразные загадки, и так, наверное, будет всегда. Египетский треугольник, хоть и известен с незапамятных времён – одна из таких загадок.

Начнём с того, что он красив. Его форма проста и гармонична, на него приятно смотреть. И с ним легко работать, используя самые простые инструменты – линейку и циркуль. Он, казалось бы, даже приглашает поработать с ним. Что ж, примем приглашение и посмотрим, что у нас получится.

Несколько простых построений, в числе которых – квадраты гипотенузы и катетов, а также симметричные отображения, сразу дают нам красивые, грмоничные фигуры. Здесь мы видим и мальтийский крест, и серединное сечение пирамиды Хефрена, и фрактальный ряд убывающих (возрастающих) по размерам египетских треугольников в соответствии с правилом золотого сечения. Удивительное богатство гармоничных пропорций. И кажется, что ещё немного, и неразрешимая задача о квадратуре круга будет решена.

Впрочем, не станем уподобляться безумцам, которые изобретают вечный двигатель, ищут квадратуру круга, философский камень и книгу мёртвых. Ограничимся констатацией бесконечных возможностей создания красоты и гармонии при помощи простой верёвки, разделённой на 12 равных частей. В том числе и картины в стиле арифмизма. Картины, которая, в соответствии с определением, изображает законченное арифметическое выражение: 9 + 16 = 25. Математический и геометрический смысл очевиден. Тайное значение – наверное, на то оно и тайное, чтобы таковым оставаться. А многозначительная и почти мистическая эстетика данных форм пусть радует глаз и будоражит воображение.

Планиметрия. Страница 5

1 2 3 4 5 6 7 8 9 10 11 12

1.Теорема Пифагора

Теорема: В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Доказательство.

1. Разделим каждую сторону большого квадрата на два отрезка x и y точкой. И проведем через эти точки отрезки.

2. Тогда треугольники 1,2,3,4 равны по двум сторонам и углу между ними.

3. Т.к. сумма углов α + β = 90°, то фигура внутри большого квадрата тоже квадрат. (Все стороны = с и все углы = 90° )

4. Площадь большого квадрата равна сумме площадей малого квадрата и 4-х треугольников. (Рис.1)

Рис.1 Теорема Пифагора.

2.Египетский треугольник

Пусть дан треугольник со сторонами АВ = a, ВС = b, АС = c. При условии, что а 2 + b 2 = с 2 . Доказать, что угол, лежащий против стороны с, прямой.

Допустим, что треугольник АВС не прямоугольный. Тогда можно опустить высоту на сторону АС — h (Рис.2). Из двух прямоугольных треугольников ABD и DBC составим следующую систему уравнений по теореме Пифагора. Обозначим AD как х, BD — высота h.

Но по условию задачи а 2 + b 2 = с 2 . Следовательно х = 0 и сторона а = h. Т.е. угол между сторонами АВ и АС — прямой.

В древнем Египте данное соотношение применялось очень широко. Например для построения прямого угла между сторонами при строительстве зданий и сооружений. Или при измерении прямых углов пахотных земель. Так как зная соотношение, можно легко построить прямой угол. По этой причине треугольник со сторонами 3,4,5 ед. называют Египетским треугольником.

Рис.2 Египетский треугольник.

3.Соотношение между углами и сторонами в прямоугольном треугольнике

Пусть дан прямоугольный треугольник АВС. Проведем прямую ЕF параллельную стороне АВ (Рис.3). Тогда по теореме о пропорциональных отрезках:

Т.е. соs α не зависит от размеров прямоугольного треугольника, а зависит только от величины угла. Тогда по теореме Пифагора sin α также зависит только от величины угла. А следовательно tg α и ctg α.

Отсюда можно сделать следующие выводы:

AB = BC sin α
AC = BC cos α
AB = AC tg α
AC = AB ctg α

Рис.3 Соотношение между углами и сторонами в прямоугольном треугольнике.

4.Основные тригонометрические тождества

Пусть дан прямоугольный треугольник со сторонами a,b,c. (Рис.4)

Рис.4 Основные тригонометрические тождества.

Репетитор: Васильев Алексей Александрович

Предметы: математика, физика, информатика, экономика, программирование.

2000 руб / 120 мин — подготовка к ЕГЭ и ГИА для школьников. 3000 руб / 120 мин — индивидуально (базовый уровень). 2000 руб / 120 мин — студенты.

Тел. 8 916 461-50-69, email: alexey-it@ya.ru

5.Пример 1

У треугольника одна сторона равна 1 м, а прилегающие к ней углы 30° и 45°. Найдите другие стороны треугольника. (рис.5)

Так как один из углов 30 градусов, то катет, лежащий против этого угла равен половине гипотенузы, т.е. h = b/2. А следовательно КС = h, т.к. угол β = 45 градусов.

Рис.5 Задача. У треугольника одна сторона равна 1 м.

Пример 2

Найдите высоту равнобокой трапеции, если ее основания равны 6 м и 12 м, а боковая сторона равна 5 м. (Рис.6)

Решение:

Пусть ABCD данная трапеция. ВЕ перпендикуляр, опущенный на основание AD. Тогда АЕ = (12 — 6)/ 2 = 3 м. Так как АЕ = FD.

По теореме Пифагора:

АВ 2 = AE 2 + BE 2

Рис.6 Задача. Найдите высоту равнобокой трапеции.

Пример 3

Докажите, что расстояние между двумя точками на сторонах треугольника не больше большей из его сторон. (Рис.7)

Доказательство:

Пусть ABC данный треугольник. АС — его большая сторона. Проведем отрезок DE параллельно стороне АС. Необходимо доказать, что отрезок DE меньше стороны АС. Если мы докажем, что отрезок DE меньше большей стороны АС, то при взятии двух других точек треугольника на других его меньших сторонах, отрезок между этими точками будет также меньше стороны АС.

Опустим перпендикуляр BF на большую сторону АС. Составим следующее соотношение:

АС = АВ сos α + ВС cos β

Тогда отрезок DE будет равен:

DE = DB сos α + ВE cos β

Так как DB Рис.7 Задача. Докажите, что расстояние между двумя точками.

Пример 4

Докажите, что прямая, отстоящая от центра окружности на расстояние меньше радиуса, пересекает окружность в двух точках. (Рис.8)

Доказательство:

Пусть дана окружность с центром в точке О. И прямая а, отстоящая от центра окружности точки О, на расстояние ОЕ = h h, то прямая а будет иметь две точки пересечения. Так как

h = ОА*cos α = ОВ*cos (-α)

Радиусы ОА и ОВ можно рассматривать как две наклонные, отложенные в двух полуплоскостях, в треугольнике АОВ перпендикуляра ОЕ.

Рис.8 Задача. Докажите, что прямая, отстоящая от центра окружности.

Пример 5

Даны три положительных числа a,b,c. Докажите, что если каждое из этих чисел меньше суммы двух других, то существует треугольник со сторонами a,b,c. (Рис.9)

Доказательство:

Пусть даны три точки. Если эти три точки лежат на одной прямой, например А,Е,С, то расстояния между этими точками связаны соотношением: АС = АЕ + ЕС

Отсюда видно, что каждое из трех расстояний не больше двух других. Т.е. расстояние между точками А и С не больше двух расстояний АЕ и ЕС.

Если взять три точки, не лежащих на одной прямой, например А,В,С и опустить перпендикуляр ВЕ, то АС AB + BC (Рис.9 б). Тогда концы отрезков АВ и СВ не смогут совпасть в точке В. Так как, если даже отрезки такой же длины отложить на отрезке АС, то получится, что

Таким образом, если числа a,b и с принять за длины отрезков, то концы отрезков АВ и СВ не смогут совпасть в одной точке В. Между ними образуется некое расстояние ВВ₁ и построить треугольник не получится.

Рис.9 Задача. Даны три положительных числа.

Высота в египетском треугольнике

Планиметрия. Страница 5

1 2 3 4 5 6 7 8 9 10 11 12

1.Теорема Пифагора

Теорема: В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Доказательство.

1. Разделим каждую сторону большого квадрата на два отрезка x и y точкой. И проведем через эти точки отрезки.

2. Тогда треугольники 1,2,3,4 равны по двум сторонам и углу между ними.

3. Т.к. сумма углов α + β = 90°, то фигура внутри большого квадрата тоже квадрат. (Все стороны = с и все углы = 90° )

4. Площадь большого квадрата равна сумме площадей малого квадрата и 4-х треугольников. (Рис.1)

Рис.1 Теорема Пифагора.

2.Египетский треугольник

Пусть дан треугольник со сторонами АВ = a, ВС = b, АС = c. При условии, что а 2 + b 2 = с 2 . Доказать, что угол, лежащий против стороны с, прямой.

Допустим, что треугольник АВС не прямоугольный. Тогда можно опустить высоту на сторону АС — h (Рис.2). Из двух прямоугольных треугольников ABD и DBC составим следующую систему уравнений по теореме Пифагора. Обозначим AD как х, BD — высота h.

Но по условию задачи а 2 + b 2 = с 2 . Следовательно х = 0 и сторона а = h. Т.е. угол между сторонами АВ и АС — прямой.

В древнем Египте данное соотношение применялось очень широко. Например для построения прямого угла между сторонами при строительстве зданий и сооружений. Или при измерении прямых углов пахотных земель. Так как зная соотношение, можно легко построить прямой угол. По этой причине треугольник со сторонами 3,4,5 ед. называют Египетским треугольником.

Рис.2 Египетский треугольник.

3.Соотношение между углами и сторонами в прямоугольном треугольнике

Пусть дан прямоугольный треугольник АВС. Проведем прямую ЕF параллельную стороне АВ (Рис.3). Тогда по теореме о пропорциональных отрезках:

Т.е. соs α не зависит от размеров прямоугольного треугольника, а зависит только от величины угла. Тогда по теореме Пифагора sin α также зависит только от величины угла. А следовательно tg α и ctg α.

Отсюда можно сделать следующие выводы:

AB = BC sin α
AC = BC cos α
AB = AC tg α
AC = AB ctg α

Рис.3 Соотношение между углами и сторонами в прямоугольном треугольнике.

4.Основные тригонометрические тождества

Пусть дан прямоугольный треугольник со сторонами a,b,c. (Рис.4)

Рис.4 Основные тригонометрические тождества.

5.Пример 1

У треугольника одна сторона равна 1 м, а прилегающие к ней углы 30° и 45°. Найдите другие стороны треугольника. (рис.5)

Так как один из углов 30 градусов, то катет, лежащий против этого угла равен половине гипотенузы, т.е. h = b/2. А следовательно КС = h, т.к. угол β = 45 градусов.

Рис.5 Задача. У треугольника одна сторона равна 1 м.

Пример 2

Найдите высоту равнобокой трапеции, если ее основания равны 6 м и 12 м, а боковая сторона равна 5 м. (Рис.6)

Решение:

Пусть ABCD данная трапеция. ВЕ перпендикуляр, опущенный на основание AD. Тогда АЕ = (12 — 6)/ 2 = 3 м. Так как АЕ = FD.

По теореме Пифагора:

АВ 2 = AE 2 + BE 2

Рис.6 Задача. Найдите высоту равнобокой трапеции.

Пример 3

Докажите, что расстояние между двумя точками на сторонах треугольника не больше большей из его сторон. (Рис.7)

Доказательство:

Пусть ABC данный треугольник. АС — его большая сторона. Проведем отрезок DE параллельно стороне АС. Необходимо доказать, что отрезок DE меньше стороны АС. Если мы докажем, что отрезок DE меньше большей стороны АС, то при взятии двух других точек треугольника на других его меньших сторонах, отрезок между этими точками будет также меньше стороны АС.

Опустим перпендикуляр BF на большую сторону АС. Составим следующее соотношение:

АС = АВ сos α + ВС cos β

Тогда отрезок DE будет равен:

DE = DB сos α + ВE cos β

Так как DB Рис.7 Задача. Докажите, что расстояние между двумя точками.

Пример 4

Докажите, что прямая, отстоящая от центра окружности на расстояние меньше радиуса, пересекает окружность в двух точках. (Рис.8)

Доказательство:

Пусть дана окружность с центром в точке О. И прямая а, отстоящая от центра окружности точки О, на расстояние ОЕ = h h, то прямая а будет иметь две точки пересечения. Так как

h = ОА*cos α = ОВ*cos (-α)

Радиусы ОА и ОВ можно рассматривать как две наклонные, отложенные в двух полуплоскостях, в треугольнике АОВ перпендикуляра ОЕ.

Рис.8 Задача. Докажите, что прямая, отстоящая от центра окружности.

Пример 5

Даны три положительных числа a,b,c. Докажите, что если каждое из этих чисел меньше суммы двух других, то существует треугольник со сторонами a,b,c. (Рис.9)

Доказательство:

Пусть даны три точки. Если эти три точки лежат на одной прямой, например А,Е,С, то расстояния между этими точками связаны соотношением: АС = АЕ + ЕС

Отсюда видно, что каждое из трех расстояний не больше двух других. Т.е. расстояние между точками А и С не больше двух расстояний АЕ и ЕС.

Если взять три точки, не лежащих на одной прямой, например А,В,С и опустить перпендикуляр ВЕ, то АС AB + BC (Рис.9 б). Тогда концы отрезков АВ и СВ не смогут совпасть в точке В. Так как, если даже отрезки такой же длины отложить на отрезке АС, то получится, что

Таким образом, если числа a,b и с принять за длины отрезков, то концы отрезков АВ и СВ не смогут совпасть в одной точке В. Между ними образуется некое расстояние ВВ₁ и построить треугольник не получится.

Рис.9 Задача. Даны три положительных числа.

Египетский треугольник — загадка древности

Известный математик Пифагор совершил множество различных открытий, но большинству людей, которым не приходится регулярно сталкиваться с алгеброй и геометрией, он известен благодаря своей теореме. Ученый открыл ее, пребывая в Египте, где его очаровала красота и изящность пирамид, а это, в свою очередь, натолкнуло его на мысль о том, что в их формах прослеживается определенная закономерность.

История открытия

Своим названием египетский треугольник обязан эллинам, которые часто посещали Египет в VII-V веках до н. э., среди них был и Пифагор. Основой пирамиды Хеопса является прямоугольный многоугольник, а

Применение

Египетский треугольник с древности пользовался популярностью в архитектуре и строительстве.

Соотношение сторон этого треугольника 3:4:5 приводит к тому, что он является прямоугольным, т. е. один угол равен 90 градусам, а два других – 53,13 и 36,87 градусам. Прямым является угол между сторонами, соотношение которых равно 3:4.

Доказательство

При помощи некоторых простых вычислений можно доказать, что треугольник является прямоугольным. Если следовать теореме обратной той, которую создал Пифагор, т. е. в случае, если сумма квадратов двух сторон будет равняться квадрату третьей, то он прямоугольный, а поскольку его стороны приводят к равенству 3 2 х 4 2 = 5 2 , следовательно, он является прямоугольным.
Подводя итог, надо отметить, что египетский треугольник, свойства которого уже в течение многих столетий известны человечеству, на сегодняшний день продолжает использоваться в архитектуре. Это вовсе неудивительно, ведь такой способ гарантирует точность, которая очень важна при строительстве. Кроме этого, он очень прост в использовании, что тоже значительно облегчает процесс. Все преимущества использования этого метода прошли проверку веками и остаются популярными до сих пор.

Египетский треугольник

Египетский треугольник – прямоугольный треугольник с отношением сторон 3:4:5. Это наиболее простой из треугольников, стороны и площади которых выражаются целыми числами. Он представляет собой прекрасную иллюстрацию теоремы Пифагора – действительно, квадрат его гипотенузы (25) очевидно равен сумме квадратов его катетов (9 и 16). Предполагается даже, что именно знакомство с египетским треугольником сподвигло Пифагора на формулировку его теоремы. Впрочем, как всегда в подобных случаях, историки древности, которые не являются специалистами ни в одной другой области знания, кроме истории (и уж точно плохо смыслят в математике), могут ошибаться.

Так или иначе, имеются многочисленные указания на то, что теорема Пифагора вообще и египетский треугольник в частности были известны и широко использовались за много веков до Пифагора и далеко за пределами Египта – в Месопотамии, в долине Инда, в древнем Китае. И вправду, корень многих знаний следует искать, наверное, в практической деятельности человека. Как только возникла необходимость возводить здания и сооружения, человек эмпирическим путём пришёл к пониманию важности прямых углов. А как отмерить прямой угол, не имея геодезических приборов?

Оказывается, очень просто. Берём верёвку и делим её на 12 равных частей – например, при помощи складывания. Выбираем отрезок верёвки, равный 5, так, чтобы он находился межды двумя другими, равными 3 и 4. Выпрямляем его и фиксируем на ровном участке земли при помощи двух колышков. А затем натягиваем концы верёвки и сводим их в одну точку, чтобы получился треугольник. Прямоугольный, египетский.

«Делай, как делается». Знаменитая древнеегипетская пословица, дошедшая до наших дней. У нас её обычно понимают, как мудрое наблюдение: если так получается, значит, так правильно. Но при этом часто забывают культурно-исторический контекст Древнего Египта. Всеми работами руководили жрецы – члены замкнутой касты харнителей священного, древнего знания. Поэтому «делай, как делается» в древнеегипетском контексте наверняка значило «делай как говорят и не задавай лишних вопросов». То есть жрецы знали не только, «как» делать, чтобы «делалось», но и «почему», и это зание было скрыто от непосвящённых.

Мы тоже хотим знать, «почему». Нам недостаточно «как». Человеческий ум будоражат разнообразные загадки, и так, наверное, будет всегда. Египетский треугольник, хоть и известен с незапамятных времён – одна из таких загадок.

Начнём с того, что он красив. Его форма проста и гармонична, на него приятно смотреть. И с ним легко работать, используя самые простые инструменты – линейку и циркуль. Он, казалось бы, даже приглашает поработать с ним. Что ж, примем приглашение и посмотрим, что у нас получится.

Несколько простых построений, в числе которых – квадраты гипотенузы и катетов, а также симметричные отображения, сразу дают нам красивые, грмоничные фигуры. Здесь мы видим и мальтийский крест, и серединное сечение пирамиды Хефрена, и фрактальный ряд убывающих (возрастающих) по размерам египетских треугольников в соответствии с правилом золотого сечения. Удивительное богатство гармоничных пропорций. И кажется, что ещё немного, и неразрешимая задача о квадратуре круга будет решена.

Впрочем, не станем уподобляться безумцам, которые изобретают вечный двигатель, ищут квадратуру круга, философский камень и книгу мёртвых. Ограничимся констатацией бесконечных возможностей создания красоты и гармонии при помощи простой верёвки, разделённой на 12 равных частей. В том числе и картины в стиле арифмизма. Картины, которая, в соответствии с определением, изображает законченное арифметическое выражение: 9 + 16 = 25. Математический и геометрический смысл очевиден. Тайное значение – наверное, на то оно и тайное, чтобы таковым оставаться. А многозначительная и почти мистическая эстетика данных форм пусть радует глаз и будоражит воображение.

🎦 Видео