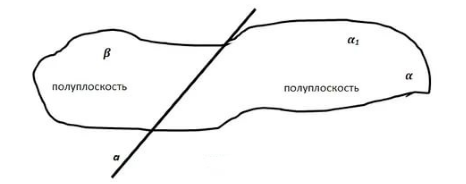
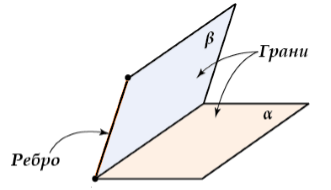
Двугранный угол между треугольниками (8 видео)

Двугранный угол между треугольниками

Замечание . Иногда говорят, что двугранный угол α a β образован двумя полуплоскостями α и β , имеющими общую граничную прямую a .

Фигуры, образованные двумя страницами одной книги, двумя соседними гранями куба, — модели двугранного угла.

Для измерения двугранного угла введём понятие его линейного угла. На ребре a двугранного угла α a β отметим произвольную точку O и в гранях α и β проведём из точки O соответственно лучи OA и OB , перпендикулярные ребру a (рис. 96, а ). Угол AOB , образованный этими лучами, называется линейным углом двугранного угла α a β .

Так как OA ⊥ a и OB ⊥ a , то плоскость AOB перпендикулярна прямой a . Это означает, что линейный угол двугранного угла есть пересечение данного двугранного угла и плоскости, перпендикулярной его ребру .

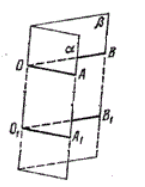
Вследствие произвольного выбора точки O на ребре двугранного угла заключаем, что двугранный угол имеет бесконечное множество линейных углов. Докажем, что все они равны. Действительно, рассмотрим два линейных угла AOB и A 1 O 1 B 1 двугранного угла α a β (рис. 96, б ). Лучи OA и O 1 A 1 лежат в одной грани α и перпендикулярны прямой a — ребру двугранного угла, поэтому они сонаправлены. Аналогично получаем, что сонаправлены лучи OB и O 1 B 1 . Тогда ∠ AOB = ∠ A 1 O 1 B 1 (как углы с сонаправленными сторонами).

Таким образом, нами доказана теорема.

Теорема 27. Величина линейного угла не зависит от выбора его вершины на ребре двугранного угла.

Иначе говоря, все линейные углы данного двугранного угла равны между собой.

Это позволяет ввести следующее определение.

Определение. Величиной двугранного угла называется величина его линейного угла.

Величина двугранного угла, измеренная в градусах, принадлежит промежутку (0 ° ; 180 ° ).

На рисунке 97 изображён двугранный угол, градусная мера (величина) которого равна 30 ° . В этом случае также говорят, что двугранный угол равен тридцати градусам.

Двугранный угол является острым (рис. 98, а ), прямым (рис. 98, б ) или тупым (рис. 98, в ), если его линейный угол соответственно острый, прямой или тупой.

Заметим, что аналогично тому, как и на плоскости, в пространстве определяются смежные (рис. 99, а ) и вертикальные (рис. 99, б ) двугранные углы . При этом справедливы и аналогичные теоремы о величинах этих углов.

Попробуйте доказать самостоятельно следующие два утверждения, важные для решения задач.

 На гранях двугранного угла величины α взяты точки A и B ; A 1 и B 1 — проекции этих точек на ребро двугранного угла; AA 1 = a ; BB 1 = b ; A 1 B 1 = h . Тогда

AB = .

 Если внутри двугранного угла величины α взята точка на расстояниях a и b от граней двугранного угла, то её расстояние от ребра двугранного угла равно .

14.2. Угол между двумя плоскостями

Две пересекающиеся плоскости образуют четыре двугранных угла с общим ребром (рис. 100). Если величина одного из них равна ϕ , то величины трёх остальных равны соответственно 180 ° – ϕ , ϕ , 180 ° – ϕ (почему?). Наименьшая из этих величин принимается за величину угла между данными пересекающимися плоскостями.

Определение. Углом между двумя пересекающимися плоскостями называется наименьший из двугранных углов, образованных при их пересечении.

Угол между параллельными или совпадающими плоскостями полагается считать равным нулю.

Если величина угла между плоскостями α и β равна ϕ , то пишут: ( α ; β ) = ϕ .

Так как двугранный угол измеряется своим линейным углом, то из выше приведённого определения следует, что угол между пересекающимися плоскостями равен углу между пересекающимися прямыми, лежащими в этих плоскостях и перпендикулярными к линии их пересечения (см. рис. 100). Это означает, что величина угла между плоскостями принадлежит промежутку [0 ° ; 90 ° ] .

ЗАДаЧа. Отрезок DM длиной 3,2 перпендикулярен плоскости ромба ABCD ( ∠ ADC — тупой). Диагонали ромба равны 12 и 16. Найти углы между плоскостями:

а) ABC и MBC ; б) AMD и CMD .

Решение. а) Пусть DE — высота ромба ABCD (рис. 101). Тогда по теореме о трёх перпендикулярах ME ⊥ BC и ∠ DEM = ϕ — линейный угол двугранного угла, образованного плоскостями ABC и MBC . Найдём величину этого угла.

По условию задачи DM ⊥ ( ABC ), поэтому ⧌ MDE — прямоугольный, значит, tg ϕ = . Так как DE — высота ромба ABCD , то DE = , где S — площадь этого ромба. Сторона BC ромба является гипотенузой прямоугольного треугольника BOC , катеты OB и OC которого равны 6 и 8. Значит, BC = = = 10.

Учитывая, что S = • AC • BD = •12•16 = 96, находим: DE = = 9,6. Тогда tg ϕ = = = , откуда ϕ = arctg .

б) Так как отрезок DM — перпендикуляр к плоскости ромба ABCD , то AD ⊥ DM , CD ⊥ DM , значит, ∠ ADC = ψ — линейный угол двугранного угла, образованного пересекающимися плоскостями ADM и CDM . Найдём этот угол.

В треугольнике ACD по теореме косинусов находим

cos ψ = = = – ,

откуда ψ = arccos .

Ответ: а) arctg ; б) arccos .

Содержание

Геометрия
Понятие двугранного угла и угла между плоскостями
Перпендикулярность плоскостей
Прямоугольный параллелепипед
Трехгранный угол
Двугранный угол
Понятие двугранного угла
Градусная мера двугранного угла
Готовые работы на аналогичную тему
Примеры задач
🎥 Видео

Видео:10 класс, 22 урок, Двугранный уголСкачать

Геометрия

План урока:

Видео:№174. Найдите двугранный угол ABCD тетраэдра ABCD, если углы DAB, DAC и ACB прямые, ACСкачать

Понятие двугранного угла и угла между плоскостями

Напомним, что в планиметрии углом называют фигуру, состоящую из точки и двух лучей, выходящих из нее. Сама точка именуется вершиной угла, а лучи – сторонами угла.

По аналогии в стереометрии рассматривается схожая фигура – двугранный угол. Он состоит из двух полуплоскостей, которые исходят из одной прямой. Каждая из этих полуплоскостей именуется гранью двугранного угла, а их общая прямая – это ребро двугранного угла.

Для обозначения двугранного угла достаточно указать две точки на его ребре, а также ещё по одной точке на каждой грани. Например, на следующем рисунке показан угол САВD:

Двугранные углы часто встречаются в обычной жизни. Например, его образуют двухскатные крыши домов. В стереометрии двугранные угла можно найти в любом многограннике.

Двугранные углы можно измерять. Для этого надо выбрать произвольную точку на ребре угла и на каждой грани построить перпендикуляр, проходящий через эту точку. Через эти два перпендикуляра можно построить единственную плоскость. Угол между двумя перпендикулярами и принимается за величину двугранного угла.

Отдельно отметим, что плоскость, проходящая через перпендикуляры (на рисунке выше это γ) перпендикулярна ребру угла АВ. Это вытекает из признака перпендикулярности прямой и плоскости. Действительно, АВ⊥ВС и АВ⊥BD, поэтому и АВ⊥γ. Построенный угол ∠СBD называют линейным углом двугранного угла.

Понятно, что в каждом двугранном угле можно построить сколько угодно линейных углов:

Здесь помимо ∠ВСD построены линейные углы ∠В’С’D’ и ∠В’’С’’D’’. Однако все эти углы имеют одинаковую градусную меру. Сравним, например, ∠ВСD и ∠В’С’D’. Так как BD⊥AB и B’D’⊥АВ, то BD||B’D’. Аналогично можно прийти к выводу, что ВС||B’C’. Получаем, что стороны углов ∠ВСD и ∠В’С’D’ – это сонаправленные лучи, а потому ∠ВСD и ∠В’С’D’ одинаковы.

Двугранные углы, как и обычные углы, можно разделить на острые (их градусная мера меньше 90°), прямые (они в точности равны 90°) и тупые (которые больше 90°).

Если две плоскости пересекаются, то они образуют сразу 4 двугранных угла. Если среди них есть острый угол, то его величина считается углом между плоскостями. Если же все образуется 4 прямых двугранных угла, то угол между плоскостями принимается равным 90°.

Видео:ДВУГРАННЫЕ УГЛЫ ЧАСТЬ I #shorts #егэ #огэ #математика #профильныйегэСкачать

Перпендикулярность плоскостей

В частном случае, когда угол составляет 90°, говорят, что пересекающиеся плоскости перпендикулярны.

Перпендикулярны друг другу пол и стены в доме, смежные грани кубика, стенки коробки. Существует особый признак перпендикулярности плоскостей.

Действительно, пусть плоскости α и β пересекаются по линии n, и в β есть такая прямая m, что m⊥α. Тогда m и n должны пересекаться в какой-нибудь точке К. Проведем в плоскости α через К прямую р, перпендикулярную n. Ясно, что m⊥р, ведь m⊥α. Получается, угол между m и р как раз и является углом между плоскостями α и β, ведь m⊥n и р⊥n. И этот угол равен 90°, ведь m⊥p, ч т. д.

Из доказанного признака вытекает следующее утверждение:

Видео:№190. Дан куб ABCDA1B1C1D1. Найдите следующие двугранные углы: а) АВВ1ССкачать

Прямоугольный параллелепипед

Ранее мы уже узнали про параллелепипед. Это фигура с 6 гранями, каждая из которых представляет собой параллелограмм. Особый интерес представляет его частный случай – прямоугольный параллелепипед.

Такую форму имеют многие шкафы, другие предметы мебели, коробки для обуви, небоскребы. Изображают прямоугольный параллелепипед так:

Для обозначения вершин параллелепипеда применяют латинские буквы. Очень часто для вершин одной грани используют 4 буквы без индекса (на рисунке выше это А, В, С, D), а другие 4 вершины обозначают такими же буквами, но с нижним индексом 1: А₁, B₁, C₁ и D₁. При этом одноименные вершины (например, А и А₁) находятся на одном ребре, которое располагается на рисунке вертикально.

Докажем некоторые свойства прямоугольного параллелепипеда.

Например, ребро АD пересекается с гранями АВВ₁А₁ и CDD₁C₁. Значит, оно перпендикулярно этим граням (точнее говоря, оно перпендикулярно плоскостям, проходящим через эти грани). Действительно, AD⊥DC, ведь ∠ADC является углом в прямоугольнике АВСD и потому он прямой. Аналогично и AD⊥DD₁, ведь и ADD₁A₁ – прямоугольник. Получается, что ребро AD перпендикулярно 2 прямым в грани CDD₁C₁ (которые при этом пересекаются), и потому оно перпендикулярно и всей грани. То же самое можно продемонстрировать для любого ребра прямоугольного параллелепипеда и любой грани, которую она пересекает.

Эти грани пересекаются по ребру А₁D₁. Этому ребру в свою очередь перпендикулярны ребра АА₁ и А₁В₁, лежащие в гранях ADD₁A₁ и A₁D₁C₁B₁. Значит, ∠АА₁В₁ и будет углом между этими гранями. Но он составляет 90°, то есть грани перпендикулярны, ч. т. д.

Хотя у прямоугольного параллелепипеда есть 12 граней, многие из них имеют одинаковую длину. Поэтому для описания размеров этой фигуры достаточно указать только три параметра. Обычно их называют длиной, шириной и высотой:

Эти параметры также называют измерениями прямоугольного параллелепипеда. Зная их, можно вычислить длину диагонали прямоугольного параллелепипеда. Для этого используется следующая теорема:

Действительно, пусть есть прямоугольный параллелепипед АВСDA₁B₁C₁D₁. Назовем ребро AD его длиной, АВ – шириной, а ВВ₁ – высотой. Пусть необходимо найти длину диагонали В₁D:

Сначала построим отрезок BD и рассмотрим ∆ABD. Он прямоугольный, и потому для него верна теорема Пифагора:

Теперь перейдем к ∆В₁ВD. Так как ребро BB₁ перпендикулярно грани ABCD, то ∠В₁ВD – прямой. Тогда и ∆В₁ВD – прямоугольный, а потому и для него можно записать теорему Пифагора:

Дополнительно отметим уже известный нам факт, что тот прямоугольный параллелепипед, у которого все стороны одинаковы, именуется кубом. Можно дать и такое определение куба:

Видео:Найти двугранный угол между треугольниками ABC и BCD. Метод плоскопараллельным перемещением.Скачать

Трехгранный угол

Выберем в пространстве произвольную точку K. Далее из нее проведем три луча КА, КВ и КС так, чтобы они не находились в одной плоскости:

В результате мы получили фигуру, которую именуют трехгранным углом. Она состоит их трех плоских углов: ∠АКС, ∠АКВ и ∠ВКС. Эти углы так и называются – плоские углы трехгранного угла. Сам же трехгранный угол обозначают четырьмя буквами: КАВС. Обратите внимание, что через каждую пару лучей КА, КВ и КС можно провести плоскость. Таким образом, название «трехгранный» угол показывает, что в точке К сходятся три грани. Чаще всего в стереометрии такой угол возникает при рассмотрении вершин тетраэдра, в котором есть сразу четыре трехгранных угла:

Доказательство. Пусть в пространстве из точки D выходят лучи AD, BD и CD. Важно понимать, что мы можем свободно «передвигать» точки А, В и С по лучам, и величина плоских углов при этом меняться не будет. Если среди плоских углов нет наибольшего, то теорема очевидно выполняется. Поэтому надо рассмотреть лишь случай, когда один из углов – наибольший. Пусть им будет ∠BDC:

Это возможно сделать, ведь ∠BDC > AD, поэтому внутри ∠BDC можно провести луч DK. Далее «сместим» точку А на луче АD так, чтобы DK = AD. Естественно, что при этом плоские углы трехгранного угла никак не изменятся, также как останется верным равенство

Сравним ∆ADC и ∆DKC. У них есть общая сторона DC, одинаковы стороны DK и AD, а также совпадают углы между ними. Значит, эти треугольники равны, и тогда можно записать, что:

Теперь сравним ∆ABD и ∆DBK. У них BD – общая сторона, а DK = AD. При этом BK 1 параллельны друг другу

Видео:Двугранный угол. Признак перпендикулярности плоскостей. Видеоурок 10. Геометрия 10 классСкачать

Двугранный угол

Вы будете перенаправлены на Автор24

Видео:Определение истинной величины двугранного угла АВСD при ребре АВ методом замены плоскостей проекцииСкачать

Понятие двугранного угла

Для введения понятия двугранного угла, для начала вспомним одну из аксиом стереометрии.

Любую плоскость можно разделить на две полуплоскости прямой $a$, лежащей в этой плоскости. При этом, точки, лежащие в одной полуплоскости находятся с одной стороны от прямой $a$, а точки, лежащие в разных полуплоскостях — по разные стороны от прямой $a$ (рис. 1).

На этой аксиоме основан принцип построение двугранного угла.

Фигура называется двугранным углом, если она состоит из прямой и двух полуплоскостей этой прямой, не принадлежащих одной плоскости.

При этом полуплоскости двугранного угла называются гранями, а прямая, разделяющая полуплоскости — ребром двугранного угла (рис. 1).

Рисунок 2. Двугранный угол

Видео:10 класс - Геометрия - Двугранный уголСкачать

Градусная мера двугранного угла

Выберем на ребре произвольную точку $A$. Угол между двумя прямыми, лежащими в разных полуплоскостях, перпендикулярных ребру и пересекающихся в точке $A$ называется линейным углом двугранного угла (рис. 3).

Очевидно, что каждый двугранный угол имеет бесконечное число линейных углов.

Все линейные углы одного двугранного угла равняются между собой.

Доказательство.

Рассмотрим два линейных угла $AOB$ и $A_1_1$ (рис. 4).

Так как лучи $OA$ и $_1$ лежат в одной полуплоскости $alpha $ и перпендикулярны одной прямой, то они являются сонаправленными. Так как лучи $OB$ и $_1$ лежат в одной полуплоскости $beta $ и перпендикулярны одной прямой, то они являются сонаправленными. Следовательно

[angle AOB=angle A_1_1]

В силу произвольности выборов линейных углов. Все линейные углы одного двугранного угла равны между собой.

Теорема доказана.

Готовые работы на аналогичную тему

Градусной мерой двугранного угла называется градусная мера линейного угла двугранного угла.

Видео:Урок 8. Угол между плоскостями. Стереометрия с нуля.Скачать

Примеры задач

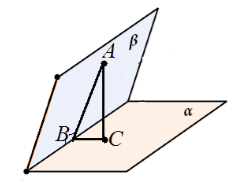
Пусть нам даны две неперпендикулярные плоскости $alpha $ и $beta $ которые пересекаются по прямой $m$. Точка $A$ принадлежит плоскости $beta $. $AB$ — перпендикуляр к прямой $m$. $AC$ перпендикуляр к плоскости $alpha $ (точка $C$ принадлежит $alpha $). Доказать, что угол $ABC$ является линейным углом двугранного угла.

Доказательство.

Изобразим рисунок по условию задачи (рис. 5).

Для доказательства вспомним следующую теорему

Теорема 2: Прямая, проходящая через основание наклонной, перпендикулярно ей, перпендикулярна её проекции.

Так как $AC$ — перпендикуляр к плоскости $alpha $, то точка $C$ — проекция точки $A$ на плоскость $alpha $. Следовательно, $BC$ — проекция наклонной $AB$. По теореме 2, $BC$ перпендикулярна ребру двугранного угла.

Тогда, угол $ABC$ удовлетворяет всем требованиям определения линейного угла двугранного угла.

Двугранный угол равен $30^circ$. На одной из граней лежит точка $A$, которая удалена от другой грани на расстояние $4$ см. Найти расстояние от точки $A$ до ребра двугранного угла.

Решение.

Будем рассматривать рисунок 5.

По условию, имеем $AC=4 см$.

По определению градусной меры двугранного угла, имеем, что угол $ABC$ равен $30^circ$.

Треугольник $ABC$ является прямоугольным треугольником. По определению синуса острого угла

Ответ: $10$ см.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 27 04 2021