Движение треугольника осевая симметрия (6 видео)

Осевая симметрия является движением

Осевая симметрия является движением.

Пусть A и B — две произвольные точки фигуры F.

При симметрии относительно прямой g фигуры F точка A переходит в точку A1, точка B — в точку B1. При этом AO=A1O, BO1=B1O1и прямая g перпендикулярна отрезкам AA1 и BB1.

Проведём отрезки AO1 и A1O1.

Прямоугольные треугольники AOO1 и A1OO1 равны по двум катетам, следовательно, AO1=A1O1 и ∠OAO1=∠OA1O1.

Прямые AA1 и BB1 параллельны по признаку параллельности прямых (как прямые, перпендикулярные одной и той же прямой g).

∠BO1A=∠OAO1 (как внутренние накрест лежащие при AA1 ∥ BB1 и секущей AO1)

∠B1O1A1=∠OA1O1 (как внутренние накрест лежащие при AA1 ∥ BB1 и секущей A1O1)

В треугольниках BO1A и B1O1A1:

Следовательно, эти треугольники равны (по двум сторонам и углу между ними).

Из равенства треугольников следует равенство соответствующих сторон: AB=A1B1, то есть расстояние между точками сохраняется, а значит, преобразование симметрии относительно прямой есть движение.

Что и требовалось доказать.

Содержание

One Comment
Осевая и центральная симметрия
Что такое симметрия
Осевая симметрия
Центральная симметрия
Задачи на самопроверку
Урок «Движения. Осевая симметрия»
🔍 Видео

Видео:Осевая симметрия. 6 класс.Скачать

One Comment

Добротное классическое обоснование осевой симметрии как движения, ключевым свойством которого является сохранение расстояния между двумя точками плоскости при их движении.

Видео:Осевая симметрия, как начертить треугольники симметричноСкачать

Осевая и центральная симметрия

О чем эта статья:

Видео:8 класс, 9 урок, Осевая и центральная симметрияСкачать

Что такое симметрия

Симметрия — это соразмерность, пропорциональность частей чего-либо, расположенных по обе стороны от центра. Говоря проще, если обе части от центра одинаковы, то это симметрия.

Ось симметрии фигуры — это прямая, которая делит фигуру на две симметричные части. Чтобы наглядно понять, что такое ось симметрии, внимательно рассмотрите рисунок.

Центр симметрии — это точка, в которой пересекаются все оси симметрии.

Вернемся к рисунку: на нем мы видим фигуры, имеющие ось и центр симметрии.

Рассмотрите фигуры с осевой и центральной симметрией.

Ось симметрии угла — биссектриса.
Ось симметрии равностороннего треугольника — биссектриса, медиана, высота.
Оси симметрии прямоугольника проходят через середины его сторон.
У ромба две оси симметрии — прямые, содержащие его диагонали.
У квадрата 4 оси симметрии, так как он сразу и квадрат, и ромб.
Ось симметрии окружности — любая прямая, проведенная через ее центр.

Витрувианский человек да Винчи — хрестоматийный пример симметрии. Принято считать, что, чем предмет симметричнее, тем он красивее. Хотя, по секрету, в природе нет ничего абсолютно симметричного, так уж задумано. Вся идеальная симметрия — дело рук человека.

Видео:Геометрия 8 класс (Урок№7 - Осевая и центральная симметрия.)Скачать

Осевая симметрия

Вот как звучит определение осевой симметрии:

Осевой симметрией называется симметрия, проведенная относительно прямой. При осевой симметрии любой точке, расположенной по одну сторону прямой, всегда соответствует другая точка на второй стороне этой прямой.

При этом отрезки, соединяющие эти точки, перпендикулярны оси симметрии.

Осевая симметрия часто встречается в повседневной жизни. К сожалению, не на фото в паспорте и не в стрелках на глазах. Но её вполне себе можно встретить в половинках авокадо, на морде кота или в зданиях вокруг. Осевая симметрия — неотъемлемая часть архитектуры. Оглядитесь и поищите примеры осевой симметрии вокруг вас.

В геометрии есть фигуры, обладающие осевой симметрией: квадрат, треугольник, ромб, прямоугольник.

Давайте разберемся, как построить фигуру, симметричную данной относительно прямой.

Пример 1. Постройте треугольник A₁B₁C₁ ,симметричный треугольнику ABC относительно прямой.

Проведем из вершин треугольника ABC три прямые, перпендикулярные оси симметрии, выведем эти прямые на другую сторону оси симметрии.
Найдем расстояние от вершин треугольника ABC до точек на оси симметрии.
С другой стороны прямой отложим такие же расстояния.
Соединяем точки отрезками и строим треугольник A₁B₁C₁, симметричный треугольнику ABC.
Получаем два треугольника, симметричных относительно оси симметрии.

Пример 2. Постройте треугольник, симметричный треугольнику ABC относительно прямой d.

Строим по уже известному алгоритму. Проводим прямые, перпендикулярные прямой d, из вершин треугольника ABC и выводим их на другую сторону оси симметрии.
Измеряем расстояние от вершин до точек на прямой.
Откладываем такие же расстояния на другой стороне оси симметрии.
Соединяем точки и строим треугольник A₁B₁C₁.

Пример 3. Построить отрезок A₁B₁, симметричный отрезку AB относительно прямой l.

Проводим через точку А прямую, перпендикулярную прямой l.
Проводим через точку В прямую, перпендикулярную прямой l.
Измеряем расстояния от точек А и В до прямой l.
Откладываем такое же расстояние на перпендикулярных прямых от прямой l по другую сторону и ставим точки A₁ и B₁.
Соединяем точки A₁ и B₁.

Больше примеров и увлекательных заданий — на курсах по математике в онлайн-школе Skysmart!

Видео:Центральная симметрия. 6 класс.Скачать

Центральная симметрия

Теперь поговорим о центральной симметрии — вот ее определение:

Центральной симметрией называется симметрия относительно точки.

Фигуры с центральной симметрией, как и фигуры с осевой симметрией, окружают нас повсюду. Центральную симметрию можно заметить в живой природе, в разрезе фруктов и в цветах.

Давайте разберемся, как построить центральную симметрию и рассмотрим алгоритм построения фигур с центральной симметрией.

Пример 1: Постройте треугольник A₁B₁C₁ ,симметричный треугольнику ABC, относительно центра (точки О).

Соединяем точки ABC c центром и выводим эти прямые на другую сторону оси.
Измеряем отрезки AO, BO, CO и откладываем равные им отрезки с другой стороны от центра (точки О).
Получившиеся точки соединяем отрезками A₁B₁ A₁C₁ B₁C₁.
Получаем треугольник A₁B₁C₁, симметричный треугольнику ABC, относительно центра.

Пример 2. Построить отрезок A₁B₁, симметричный отрезку AB относительно центра (точки О).

Измеряем расстояние от точки B до точки О и от точки А до точки О.
Проводим прямую из точки А через точку О и выводим ее на другую сторону.
Проводим прямую из точки B через точку О и выводим ее на другую сторону.
Чертим на противоположной стороне отрезки А₁О и B₁О, равные отрезкам АО и АB.
Соединяем точки A₁ и B₁ и получаем отрезок A₁B₁, симметричный данному.

Видео:11 класс, 10 урок, Осевая симметрияСкачать

Задачи на самопроверку

В 8 классе геометрия — сплошная симметрия: центральная, осевая, зеркальная да какая угодно. Чтобы во всем этом не поплыть, больше тренируйтесь. Чертите и приглядывайтесь, угадывайте вид симметрии и решайте больше задачек. Вот несколько упражнений для тренировки. Мы в вас очень верим!

Задачка 1. Рассмотрите симметричные геометрические рисунки и назовите вид симметрии.

Мы рассмотрели примеры осевой и центральной симметрии и знаем, что:

Симметрия относительно прямой — осевая
Симметрия относительно точки — центральная

Задачка 2. Пусть M и N какие-либо точки, l — ось симметрии. М₁ и N₁ — точки,
симметричные точкам M и N относительно прямой l. Докажите, что MN = М₁N₁.

Подсказка: опустите перпендикуляры из точек N и N₁ на прямую MМ₁.

Задачка 3. Постройте фигуру, симметричную данной относительно прямой a.

Видео:Осевая и центральная симметрия, 6 классСкачать

Урок «Движения. Осевая симметрия»

Краткое описание документа:

ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:

Мы продолжаем знакомство с движением.

На прошлом занятии вы познакомились с одним из видов движения — центральной симметрией.

Вспомним, что центральная симметрия — это такое отображение пространства на себя, при котором любая точка К переходит в симметричную ей точку К1, относительно центра симметрии точки В.

Отображение пространства на себя, при котором любая точка К переходит в симметричную ей точку К1 относительно оси а называется осевой симметрией с осью а.

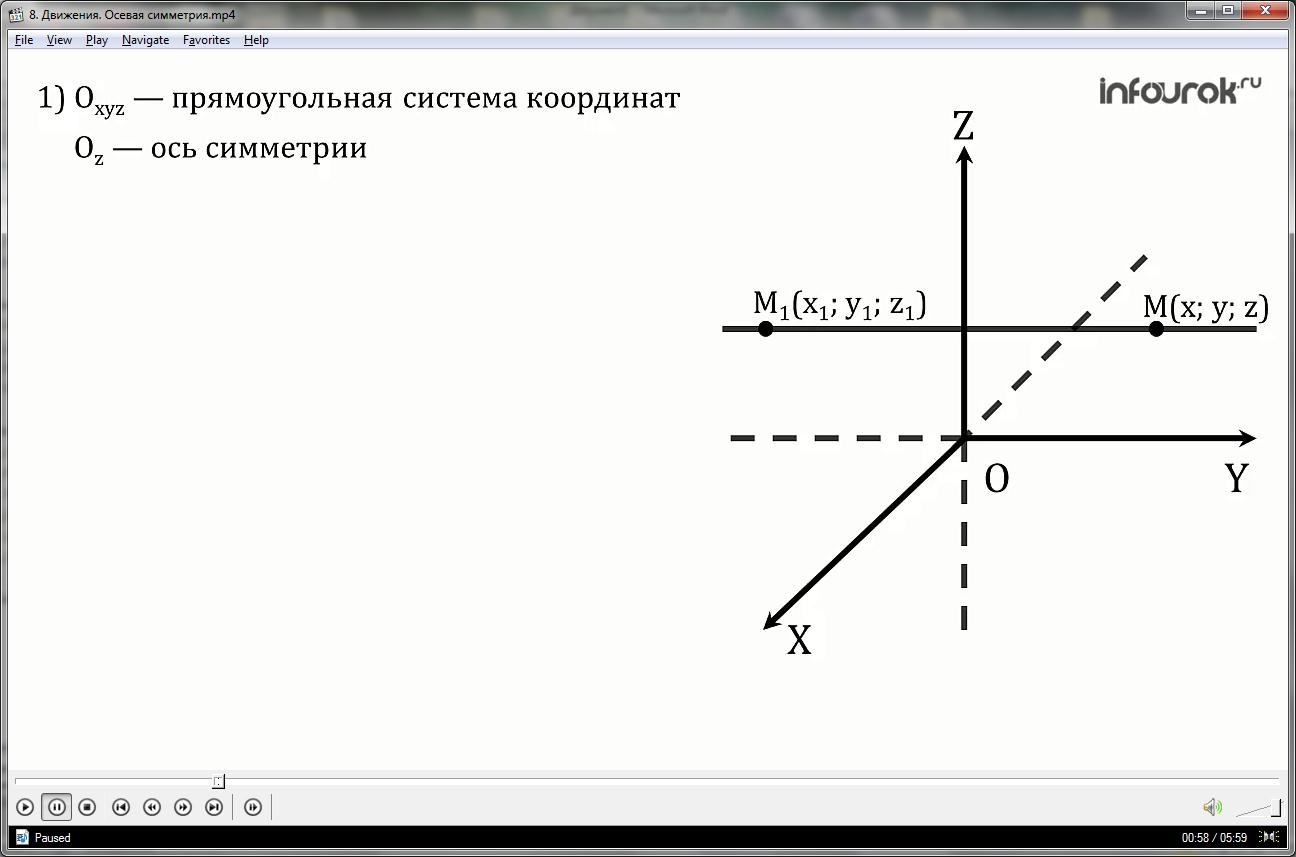
1. Введём декартову (прямоугольную) систему координат Оxyz так, чтобы ось Оz совпала с осью симметрии.

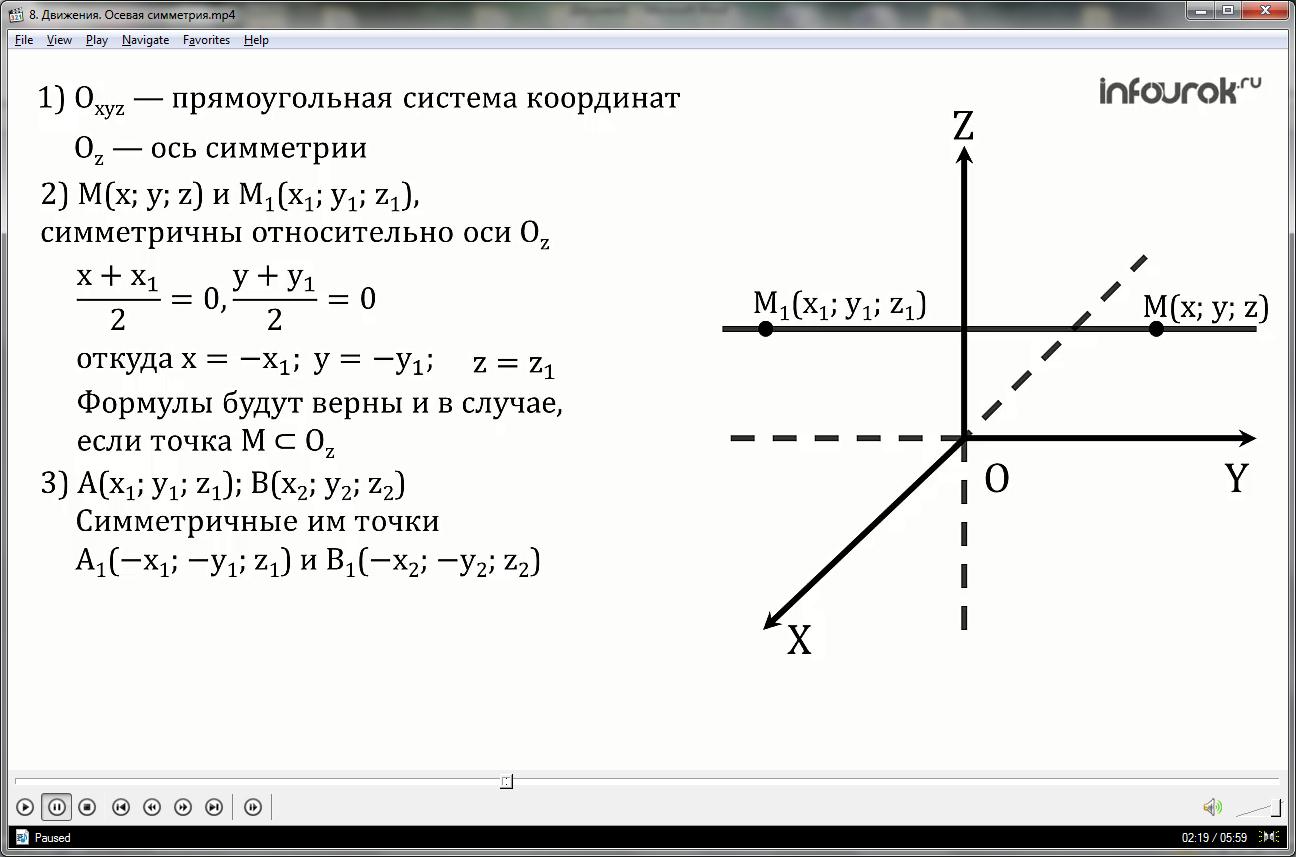
2.Найдем связь между точками М (x;y;z) и M1 (x1;y1;z1), которые симметричны относительно оси Оz .Если точка М не принадлежит оси Оz, то данная ось:

а) проходит через середину отрезка МM1;

б) перпендикулярна отрезку ММ1.

Из первого условия по формулам для координат середины отрезка имеем:

Из второго условия можно сделать вывод, о том, что z=z1.

Данные формулы будут верны и в случае, если точка М принадлежит оси Оz.

3. Рассмотрим любые две точки: А — с координатами (x1;y1;z1) и В — с координатами (x2;y2;z2) и докажем, что расстояние между точками А1 и В1, которые им симметричны, равно АВ.

Точки А1 и В1 имеют координаты

А1 (-x1;-y1;z1) и В1 (-x2;-y2;z2).

По формуле расстояний между двумя точками, найдём:

Очевидно, что длина отрезка АВ равна длине отрезка A1B1, то есть расстояние между точками сохранено.

Таким образом, мы доказали, что осевая симметрия является движением.

Рассмотрим решение задач, применяя полученные знания.

Доказать, что при осевой симметрии прямая, образующая с осью симметрии угол , отображается на прямую, так же образующую с осью симметрии угол

1. Так как ось симметрии а и прямая l не параллельны, то а пересекается с l в некоторой точке А.

Выберем любую точку N на прямой l.