Движение частицы по окружности

Видео:Движение тела по окружности с постоянной по модулю скоростью | Физика 9 класс #18 | ИнфоурокСкачать

Тестирование онлайн

Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным, оно является равноускоренным.

Видео:Криволинейное, равномерное движение материальной точки по окружности. 9 класс.Скачать

Угловая скорость

Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.

Видео:Физика - движение по окружностиСкачать

Период и частота

Период вращения T — это время, за которое тело совершает один оборот.

Частота вращение — это количество оборотов за одну секунду.

Частота и период взаимосвязаны соотношением

Связь с угловой скоростью

Видео:Движение заряженной частицы в магнитном поле | Физика ЕГЭ с Никитой АрхиповымСкачать

Линейная скорость

Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.

Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено — это есть период T. Путь, который преодолевает точка — это есть длина окружности.

Видео:Урок 276. Сила Лоренца. Движение заряженных частиц в магнитном полеСкачать

Центростремительное ускорение

При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.

Используя предыдущие формулы, можно вывести следующие соотношения

Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.

Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.

Видео:Физика 10 класс (Урок№4 - Равномерное движение точки по окружности.)Скачать

Вращение Земли

Земля участвует в двух основных вращательных движениях: суточном (вокруг своей оси) и орбитальном (вокруг Солнца). Период вращения Земли вокруг Солнца составляет 1 год или 365 суток. Вокруг своей оси Земля вращается с запада на восток, период этого вращения составляет 1 сутки или 24 часа. Широтой называется угол между плоскостью экватора и направлением из центра Земли на точку ее поверхности.

Видео:Урок 89. Движение по окружности (ч.1)Скачать

Связь со вторым законом Ньютона

Согласно второму закону Ньютона причиной любого ускорения является сила. Если движущееся тело испытывает центростремительное ускорение, то природа сил, действием которых вызвано это ускорение, может быть различной. Например, если тело движется по окружности на привязанной к нему веревке, то действующей силой является сила упругости.

Если тело, лежащее на диске, вращается вместе с диском вокруг его оси, то такой силой является сила трения. Если сила прекратит свое действие, то далее тело будет двигаться по прямой

Видео:Урок 43. Криволинейное движение. Равномерное движение по окружности. Центростремительное ускорениеСкачать

Как вывести формулу центростремительного ускорения

Рассмотрим перемещение точки на окружности из А в В. Линейная скорость равна v_A и v_B соответственно. Ускорение — изменение скорости за единицу времени. Найдем разницу векторов.

Разница векторов есть . Так как , получим

Видео:Кинематика. Движение по окружности. Урок 4Скачать

Движение по циклоиде*

В системе отсчета, связанной с колесом, точка равномерно вращается по окружности радиуса R со скоростью , которая изменяется только по направлению. Центростремительное ускорение точки направлено по радиусу к центру окружности.

Теперь перейдем в неподвижную систему, связанную с землей. Полное ускорение точки А останется прежним и по модулю, и по направлению, так как при переходе от одной инерциальной системы отсчета к другой ускорение не меняется. С точки зрения неподвижного наблюдателя траектория точки А — уже не окружность, а более сложная кривая (циклоида), вдоль которой точка движется неравномерно.

Мгновенная скорость определяется по формуле

Видео:Физика | Равномерное движение по окружностиСкачать

Движение по окружности с постоянной по модулю скоростью

теория по физике 🧲 кинематика

Криволинейное движение — движение, траекторией которого является кривая линия. Вектор скорости тела, движущегося по кривой линии, направлен по касательной к траектории. Любой участок криволинейного движения можно представить в виде движения по дуге окружности или по участку ломаной.

Движение по окружности с постоянной по модулю скоростью — частный и самый простой случай криволинейного движения. Это движение с переменным ускорением, которое называется центростремительным.

Особенности движения по окружности с постоянной по модулю скоростью:

1. Траектория движения тела есть окружность.
2. Вектор скорости всегда направлен по касательной к окружности.
3. Направление скорости постоянно меняется под действием центростремительного ускорения.
4. Центростремительное ускорение направлено к центру окружности и не вызывает изменения модуля скорости.

Видео:Движение тел по окружностиСкачать

Период, частота и количество оборотов

Пусть тело двигается по окружности беспрерывно. Когда оно сделает один оборот, пройдет некоторое время. Когда тело сделает еще один оборот, пройдет еще столько же времени. Это время не будет меняться, потому что тело движется с постоянной по модулю скоростью. Такое время называют периодом.

Период — время одного полного оборота. Обозначается буквой T. Единица измерения — секунды (с).

t — время, в течение которого тело совершило N оборотов

За один и тот же промежуток времени тело может проходить лишь часть окружности или совершать несколько единиц, десятков, сотен или более оборотов. Все зависит от длины окружности и модуля скорости.

Частота — количество оборотов, совершенных в единицу времени. Обозначается буквой ν («ню»). Единица измерения — Гц.

N — количество оборотов, совершенных телом за время t.

Период и частота — это обратные величины, определяемые формулами:

Количество оборотов выражается следующей формулой:

Пример №1. Шарик на нити вращается по окружности. За 10 секунд он совершил 20 оборотов. Найти период и частоту вращения шарика.

Видео:Равномерное движение точки по окружности | Физика 10 класс #7 | ИнфоурокСкачать

Линейная и угловая скорости

Линейная скорость

Линейная скорость — это отношение пройденного пути ко времени, в течение которого этот путь был пройден. Обозначается буквой v. Единица измерения — м/с.

l — длина траектории, вдоль которой двигалось тело за время t

Линейную скорость можно выразить через период. За один период тело делает один оборот, то есть проходить путь, равный длине окружности. Поэтому его скорость равна:

R — радиус окружности, по которой движется тело

Если линейную скорость можно выразить через период, то ее можно выразить и через частоту — величину, обратную периоду. Тогда формула примет вид:

Выразив частоту через количество оборотов и время, в течение которого тело совершало эти обороты, получим:

Угловая скорость

Угловая скорость — это отношение угла поворота тела ко времени, в течение которого тело совершало этот поворот. Обозначается буквой ω. Единица измерения — радиан в секунду (рад./с).

ϕ — угол поворота тела. t — время, в течение которого тело повернулось на угол ϕ

Радиан — угол, соответствующий дуге, длина которой равна ее радиусу. Полный угол равен 2π радиан.

За один полный оборот тело поворачивается на 2π радиан. Поэтому угловую скорость можно выразить через период:

Выражая угловую скорость через частоту, получим:

Выразив частоту через количество оборотов, формула угловой скорости примет вид:

Сравним две формулы:

Преобразуем формулу линейной скорости и получим:

Отсюда получаем взаимосвязь между линейной и угловой скоростями:

Полезные факты

• У вращающихся прижатых друг к другу цилиндров линейные скорости точек их поверхности равны: v₁ = v₂.
• У вращающихся шестерен линейные скорости точек их поверхности также равны: v₁ = v₂.
• Все точки вращающегося твердого тела имеют одинаковые периоды, частоты и угловые скорости, но разные линейные скорости. T₁ = T₂, ν₁ = ν₂, ω₁ = ω₂. Но v₁ ≠ v₂.

Пример №2. Период обращения Земли вокруг Солнца равен одному году. Радиус орбиты Земли равен 150 млн. км. Чему примерно равна скорость движения Земли по орбите? Ответ округлить до целых.

В году 365 суток, в одних сутках 24 часа, в 1 часе 60 минут, в одной минуте 60 секунд. Перемножив все эти числа между собой, получим период в секундах.

За каждую секунду Земля проходит расстояние, равное примерно 30 км.

Видео:Физика 9 класс (Урок№4 - Движение тела по окружности. Период и частота)Скачать

Центростремительное ускорение

Центростремительное ускорение — ускорение с постоянным модулем, но меняющимся направлением. Поэтому оно вызывает изменение направления вектора скорости, но не изменяет его модуль. Центростремительное ускорение обозначается как a_ц.с.. Единица измерения — метры на секунду в квадрате (м/с 2 ). Центростремительное ускорение можно выразить через линейную и угловую скорости, период, частоту и количество оборотов/время:

Пример №3. Рассчитать центростремительное ускорение льва, спящего на экваторе, в системе отсчета, две оси которой лежат в плоскости экватора и направлены на неподвижные звезды, а начало координат совпадает с центром Земли.

Спящий лев сделает один полный оборот тогда, когда Земля сделает один оборот вокруг своей оси. Земля делает это за время, равное 1 сутки. Поэтому период обращения равен 1 суткам. Количество секунд в сутках: 1 сутки = 24•60•60 секунд = 86400 секунд = 86,4∙10 3 секунд.

Радиус Земли равен 6400 км. В метрах это будет 6,4∙10 6 . Теперь у нас есть все, что нужно для вычисления центростремительного ускорения. Подставляем данные в формулу:

Алгоритм решения

1. Записать исходные данные.
2. Записать формулу для определения искомой величины.
3. Подставить известные данные в формулу и произвести вычисления.

Решение

Записываем исходные данные:

• Радиус окружности, по которой движется автомобиль: R = 100 м.
• Скорость автомобиля во время движения по окружности: v = 20 м/с.

Формула, определяющая зависимость центростремительного ускорения от скорости движения тела:

Подставляем известные данные в формулу и вычисляем:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Точка движется по окружности радиусом R с частотой обращения ν. Как нужно изменить частоту обращения, чтобы при увеличении радиуса окружности в 4 раза центростремительное ускорение точки осталось прежним?

а) увеличить в 2 раза б) уменьшить в 2 раза в) увеличить в 4 раза г) уменьшить в 4 раза

Алгоритм решения

1. Записать исходные данные.
2. Определить, что нужно найти.
3. Записать формулу зависимости центростремительного ускорения от частоты.
4. Преобразовать формулу зависимости центростремительного ускорения от частоты для каждого из случаев.
5. Приравнять правые части формул и найти искомую величину.

Решение

Запишем исходные данные:

Центростремительное ускорение определяется формулой:

Запишем формулы центростремительного ускорения для 1 и 2 случаев соответственно:

Так как центростремительное ускорение в 1 и 2 случае одинаково, приравняем правые части уравнений:

Произведем сокращения и получим:

Это значит, чтобы центростремительное ускорение осталось неизменным после увеличения радиуса окружности в 4 раза, частота должна уменьшиться вдвое. Верный ответ: «б».

pазбирался: Алиса Никитина | обсудить разбор | оценить

Видео:Движение по окружности. Нормальное и тангенциальное ускорение | 50 уроков физики (4/50)Скачать

1. Пространство и время: понятия, свойства, процедуры количественного описания Понятия пространства и времени

Видео:Движение по окружности за 1 минуту #математика #егэ2023 #егэ2023 #fyp #школа #математикапрофиль2023Скачать Содержание § 1. Движение частицы по окружности и его кинематические характеристики Описание движения по окружности. Угловые кинематические характеристики. Вектора угловой скорости и ускорения

Подобный материал:

• А. Закон инерции, 40.83kb.
• Постмодернизм план лекции: Трудность определения понятия «постмодернизм», 404.9kb.
• Воробьева Валентина Константиновна курс лекций, 273.12kb.
• Тема «Материя и движение, пространство и время» имеет важное значение для формирования, 258.39kb.
• Тема 1 основы системной концепции: понятия, сущность, атрибуты программная аннотация, 245.29kb.
• Отребляемые в настоящее время понятия образовательного нормотворчества и образовательных, 374.72kb.
• Анатолия Васильевича Мартынова, известного широкому кругу людей по книга, 5061.34kb.
• Обеспечение производства ЭВМ базовые понятия (сапр/астпп/саит), 710.17kb.
• Факультет электронной техники, пэ-04 курсоваяработ, 220.87kb.
• Линейное пространство, 700.44kb.

§ 1. Движение частицы по окружности и его кинематические характеристики

Движение материальной точки по окружности как движение с одной степенью свободы.
Понятие векторов углового перемещения, угловой скорости и углового ускорения.
Связь угловых кинематических характеристик с линейными.

Вращательное движение звезд в галактике. “Галактика Андромеда”. Фото Jason WareВведение. В предыдущих темах мы рассмотрели описание движения частиц или тел отсчета, с ними связанных. Однако важным является также описание движения систем координат, связанных с твердыми телами и служащих для пространственно-временного описания еще одного класса движений, например, различных вращений. Решив эту задачу и воспользовавшись преобразованиями Галилея, можно описать все возможные случаи движения твердых тел в любых системах отсчета.

Перед тем как приступить к изучению кинематики твердого тела, рассмотрим сначала простейший случай  движение его составных частей (материальных точек) по окружности и более общий вариант  криволинейное движение.

Описание движения по окружности. При движении частицы по окружности меняется только направление ее радиус-вектора r(t). Уравнение, характеризующее изменение положения частицы со временем, имеет вид:

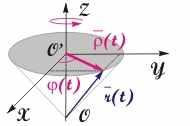
Рис. 3.1. Движение частицы по окружностиПусть радиус-вектор частицы описывает круговой конус. Тогда его сечение плоскостью ХО’У, перпендикулярной оси OZ, образует окружность радиуса  (см. рис. 3.1). В декартовой СК уравнения движения в проекциях на оси координат примут вид:

а траектория частицы будет описываться уравнением:

x 2 + y 2 =  2 . (3.3)

Вопрос. Какой вид будет иметь мировая линия при равномерном движении частицы по окружности? В рассматриваемом случае угол изменяется со временем по закону (t) = ·t + ₀, а мировая линия в трехмерном мире событий будет представлять из себя винтовую линию, нанизанную на ось Ot и имеющую шаг, равный периоду обращения частицы в плоскости вращения T = 2/. В отличии от движения по спирали значение проекции МЛ на ось Ot все время возрастает.

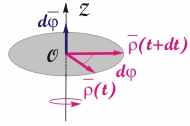
Рис. 3.2. Определение направления вектора элементарного углового перемещения по правилу буравчика (правого винта). Ручку буравчика вращаем по направлению вращения радиус-вектора частицы. Направление вектора d совпадет с направлением поступательного движения буравчика Угловые кинематические характеристики. Рассмотрим движение частицы в плоскости XY в полярных координатах. Соответствующие уравнения записываются следующим образом:

В данном случае частица обладает одной степенью свободы и ее движение удобно характеризовать зависимостью угловой координаты (угла) от времени (t).

По аналогии с понятием элементарного вектора перемещения dr введем понятие вектора элементарного углового перемещения d. За величину вектора d примем значение угла, на который повернется частица вокруг оси OZ за время dt, выраженное в радианах. Направление вектора d зададим таким образом, чтобы оно совпадало с осью вращения и определялось в соответствии с правилом правого винта (см. рис. 3.2).

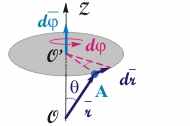
Рис. 3.3. Установление связи между направлением векторов элементарного углового и линейного перемещенийИз вышеизложенного и рис.3.3 следует, что вектора линейного и углового перемещений связаны соотношением (3.5) и не зависят от выбора начала отсчета (точки О) на оси вращения:

Чтобы быть вектором, величина должна удовлетворять четырем правилам (см. тему 2, § 3), одним из которых является подчинение закону сложения векторов.

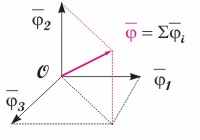
Рассмотрим случай последовательного поворота частицы на углы d₁ и d₂ вокруг произвольным образом направленных осей, проходящих через точку О. Элементарное перемещение частицы можно представить как векторную сумму, равную:

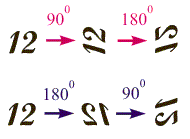
Рис. 3.5. Результаты двух серий однотипных поворотов твердого тела во взаимно перпендикулярных направлениях, проведенных в разной последовательностиТаким образом, последовательность перемещений на элементарные углы подчиняется закону сложения векторов и, следовательно, величины dи  с этой точки зрения могут быть векторами ( d при t ). Перемещения же на конечные углы этому правилу не удовлетворяют (см. примеры).

Рис. 3.4. Положение частицы и векторов ее углового перемещения в серии последовательных поворотов на 90 градусов вокруг трех взаимно перпендикулярных осей, проходящих через закрепленную точку

Из рис. 3.3 следует, что при повороте на конечный угол модуль вектора перемещения равен:

и, следовательно, векторное равенство (3.5) в общем случае не выполняется.

Для малых углов поворота оно выполняется приближенно и тем точнее, чем ближе величины 2·sin(/2) и sin( друг к другу.

Итак, введенная величина d в сравнении с понятиями перемещения, скорости и ускорения не является «естественным» вектором (точка приложения dчетко не определена и находится где-то на оси вращения). Кроме того, вектор d имеет существенный ряд ограничений, связанных с малостью поворота. В силу этих причин элементарное угловое перемещение часто называют псевдовектором.

Вектора угловой скорости и ускорения. По аналогии с линейной скоростью введем понятие мгновенной угловой скорости. Ею называется величина, равная производной от вектора углового перемещения по времени:

Выразим угловую скорость через другие известные нам векторные величины. Модуль линейной скорости равен:

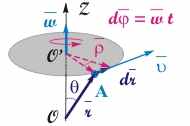
Рис. 3.6. Установление связи между направлением векторов угловой и линейной скорости.С учетом направлений векторов, указанных на рис. 3.6, скалярное равенство  = · = ·r·sin можно записать в векторном виде:

Уравнение (3.9) можно получить также, разделив выражение (3.5) на dt и воспользовавшись определениями линейной и угловой скоростей.

Понятие вектора углового ускорения введем по аналогии с поступательным движением, т. е. как производной от угловой скорости по времени:

Установим связь между линейным и угловым ускорением. Для этого продифференцируем выражение (3.11) по времени. Получим, что

В случае неподвижной оси вращения, вектора углового ускорения и угловой скорости коллинеарны (сонаправлены или направлены в противоположные стороны). Первое слагаемое в выражении (3.11) представляет собой составляющую ускорения, направленную по касательной к траектории движения частицы, а второе  вдоль радиуса  в сторону оси вращения (их называют тангенциальной и нормальной составляющими вектора ускорения). Итак, в случае движения частицы по окружности, вектора нормальной и тангенциальной составляющей ускорения равны:

Модули величин нормального, тангенциального и полного ускорений частицы рассчитываются из следующих равенств:

Вектор углового ускорения частицы при неизменной ориентации оси вращения параллелен этой оси (направлен вдоль вектора или против него в зависимости от того увеличивается или уменьшается угловая скорость).

🎥 Видео

Урок 47. Неравномерное движение по окружности. Тангенциальное ускорениеСкачать

Физика 9 класс. Движение по окружностиСкачать

Лекция 6.1 | Описание движения по окружности | Александр Чирцов | ЛекториумСкачать

Физика 10 Равномерное движение точки по окружностиСкачать

Центростремительное ускорение. 9 класс.Скачать