Две равные окружности внешне касаются друг друга и третьей окружности

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4

Упражнение 20. Докажите эту формулу. (Указание: покажите, что точки CA1JB1 являются вершинами квадрата, сторона которого равна радиусу вписанной окружности и примените формулы, выражающие отрезки касательных через стороны треугольника.)

Для радиуса вписанной окружности равнобедренного треугольника можно получить простое выражение через основание и угол при нем (смотри чертеж):

.

Видео:С4, егэ. Задача про три касающиеся друг друга окружностиСкачать

Окружность, проходящая через две вершины треугольника

Чаще всего в геометрических задачах встречается конфигурация, в которой окружность проходит только через две вершины треугольника, при этом вторично пересекая две его стороны. В такой конструкции появляются два подобных треугольника ABC и AML, у которых соответственные стороны ML и BC – не параллельны.

Рассмотрим некоторые примеры, в которых появляется такая конструкция.

Пример 1. Окружность, проходящая через две вершины и основания двух высот треугольника (В этом случае сторона AC будет диаметром окружности).

В этой конфигурации коэффициент подобия треугольников равен косинусу угла при третьей вершине: .

Упражнение 21. Докажите сформулированное выше утверждение. (Указание: выразите отрезки AM и AL через стороны треугольника и угол A.)

Взглянем на эту же конструкцию с другой стороны.

Пример 2. Пусть одна из сторон треугольника (например, BC) является диаметром окружности, а L и M точки пересечения окружности с двумя другими сторонами. Тогда из этих точек диаметр окружности виден под прямым углом.

Нетрудно увидеть, что отрезки BM и CL являются высотами треугольника.

Упражнение 22. Окружность, диаметром которой служит одна из сторон треугольника, пересекает другую сторону в точке, являющейся ее серединой. Докажите, что данный треугольник – равнобедренный.

Видео:✓ Как найти второй радиус? | Ботай со мной #105 | Борис ТрушинСкачать

Окружность, касающаяся двух сторон треугольника

На математических олимпиадах нередко предлагаются задачи, в которых рассматриваются либо угол и вписанная в него окружность, либо равнобедренный треугольник, касающийся некоторой окружности в двух своих вершинах. При этом обычно присутствует еще один элемент: секущая угла, касающаяся окружности в некоторой точке. Наблюдательный читатель уже заметил, что описанная здесь конструкция – ни что иное, как треугольник и вневписанная окружность.

При решении задач бывает полезно следующее свойство, которое кажется очевидным: длина отрезка DE равна сумме длин отрезков DB и EC.

Видео:ЕГЭ Задание 16 Три окружностиСкачать

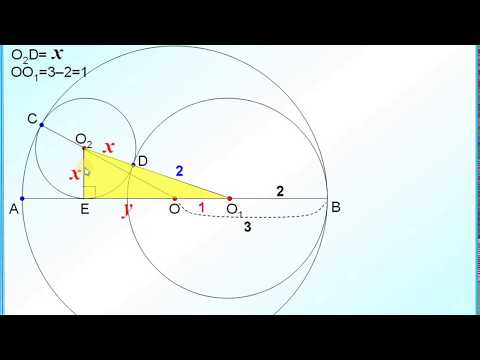
Окружность, касающаяся одной из сторон треугольника в вершине

Так как угол между хордой и касательной к окружности равен половине центрального угла, опирающегося на хорду, то изображенные на чертеже треугольники ABD и ABC имеют равные углы при вершинах B и C соответственно. А если учесть, что угол при вершине A у них общий, то нетрудно заметить, что два этих треугольника подобны.

Упражнение 23. Дайте строгое доказательство сформулированного выше утверждения.

Видео:ЕГЭ Задание 16 Две касающиеся окружностиСкачать

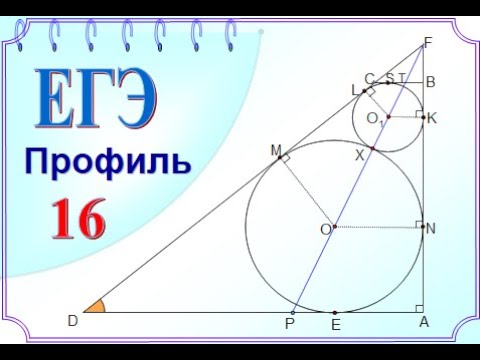
Еще раз о высотах треугольника

Через точку пересечения высот треугольника (ортоцентр), основания двух высот и третью вершину проходит окружность. Отрезок AH является диаметром этой окружности.

Рассмотрим теперь сразу две окружности, проходящие через основания высот.

Видео:Две окружности | Резерв досрока ЕГЭ-2019. Задание 16. Профильный уровень | Борис Трушин |Скачать

Продолжение темы о двух окружностях

С парой пересекающихся окружностей и треугольником связан ряд интересных конфигураций.

Первая конструкция. Две окружности пересекаются в точках A и B. Через точку B проведена секущая CD.

Упражнение 25. Докажите, что какая бы не была взята секущая, будут получаться подобные треугольники ACD.

Вторая конструкция. Две окружности пересекаются в точках A и B. CD – отрезок общей касательной к этим окружностям.

Упражнение 26. Исследуйте свойства треугольника ACD. (Смотри чертеж.)

Упражнение 27. Выразите стороны треугольника ACD через радиусы окружностей и длину хорды AB.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Задачи для самостоятельного решения

1. Две окружности внешне касаются в точке А, ВС — их общая внешняя касательная. Доказать, что .

2. Две окружности пересекаются в точках А и В. Точки А и В лежат по разные стороны от прямой l, которая пересекает окружности соответственно в точках С, D, Е и М. Доказать, что сумма углов DBE и САМ равна 180°.

3. Две окружности пересекаются в точках А и В. Прямые l1 и l2 параллельны, причем l1 проходит через точку А и пересекает окружности в точках Е и К, а l2 про­ходит через точку В и пересекает окружности в точках М и Р. Доказать, что четырехугольник ЕКМР — параллелограмм.

4. Из точки М проведены к окружности с центром в точке О касательные МА и МВ. Прямая l касается окружности в точке С и пересекает МА и МВ соответственно в точках D и Е. Доказать, что: а) периметр треугольника MDE не зависит от Выбо­ра точки С; б) угол DOE не зависит от выбора точки С.

5. Точки А, В, С и D делят окружность на части, отношение которых 1 : 3 : 5 : 6. Найти углы между касательными к окружности, проведенными в точках А, В, С и D.

6. Две равные окружности внешне касаются друг друга и третьей окружности, радиус которой равен 8 см. Отрезок, соединяющий точки касания двух равных ок­ружностей с третьей, равен 12 см. Найти радиусы равных окружностей.

7. Общая хорда двух пересекающихся окружностей равна а и служит для одной окружности стороной правильного вписанного шестиугольника: а для другой ­вписанного квадрата. Найти расстояние между центрами окружностей.

8. Две окружности радиусами, и R касаются внешним образом. Найти дли­ну их общей внешней касательной.

9. Две окружности радиусами r и R касаются внешним образом. Прямая 1 пересекает окружности в точках А, В, С и D так, что АВ = ВС = CD. Найти AD.

10. Две окружности, радиусы которых относятся как 1 : 3, касаются внешним образом, длина их общей внешней касательной см. Найти периметр фигуры, образованной внешними касательными и внешними дугами окружностей.

11. Из внешней точки к окружности проведены секущая длиной 48 см и каса­тельная, длина которой составляет от внутреннего отрезка секущей. Найти ра­диус окружности, если известно, что секущая удалена от центра на расстояние 24 см.

12. Общая внешняя касательная двух внешне касающихся окружностей составляет с линией центров угол а. Найти отношение радиусов.

13. Из точки А, расположенной вне круга с центром О, проведены секущие АВС и АМК (В и М — ближайшие к А точки окружности, лежащие на секущих). Найти ВС, если известно, что и секущая АМК проходит через центр окружности.

14. Две окружности пересекаются в точках А и В. Через точку А проведены отрезки АС и AD, каждый из которых, являясь хордой одной окружности, касается другой окружности. Доказать, что АС2 . BD = AD2 . BС.

15. АВ и CD — взаимно перпендикулярные пересекающиеся хорды окружно­сти радиуса R. Доказать, что АС2 + BD2 = 4R2.

16. Доказать, что сумма квадратов расстояний от точки М, взятой на диаметре окружности, до концов любой из параллельных этому диаметру хорд есть для дан­ной окружности постоянная величина.

17. Две окружности внешне касаются в точке С, АВ — их общая внешняя ка­сательная. Найти радиусы, если АС = 8 см, ВС = 6 см.

18. Окружности радиусами R и касаются внешним образом. Из центра мень­шей окружности под углом 30° к линии центров проведен отрезок длиной 2R. Найти длины тех частей отрезка, которые лежат вне окружностей.

Видео:Геометрия Две окружности радиусом R = 3 см и r = 1 см касаются внешним образом. Найти расстояние отСкачать

Учебное пособие. Пенза-2012 удк 514

Главная > Документ

Дано: окружность S(О),

AD – секущая, AD = 48 см,

В – точка касания,

АВ = СD,

ОК AD, ОК = 24 см.

По теореме о секущей и касательной 

, .

Имеем . Обозначим

; .

Решая квадратное уравнение, получим х = 36, DC = 36,

АС = 48 – 36 = 12, АВ = 36 = 24.

Из прямоугольного треугольника ODK:

.

Задача 4. В окружности проведены 3 хорды: МА = 6 см, МВ = 4 см, МС = 1 см. Хорда МВ делит АМС пополам. Найти радиус окружности.

МА, МВ, МС – хорды,

МА = 6 см, МВ = 4 см,

По условию АМВ = ВМС  АВ = ВС  центральные углы, опирающиеся на эти дуги, равны, то есть АОВ = ВОС.

ОА = ОВ = ОС – как радиусы окружности  АОВ = ВОС (по двум сторонам и углу между ними)  АВ = ВС.

Обозначим АМВ =  , тогда АОВ = 2  .

Из АМС и ВМС по теореме косинусов имеем:

.

Вычитая из первого равенства второе, получим:

 .

Тогда   .

Из АОВ по теореме косинусов

 

Ответ: см.

Задача 5. Н а окружности взяты четыре точки. Доказать, что прямые, соединяющие середины противолежащих дуг, взаимно перпендикулярны.

Дано: окружность S(О),

Доказать: KM  LN.

Пусть точки K, L, M, N – середины дуг АВ, ВС, СD, DА.

,



.

Задачи для самостоятельного решения.

В круге радиуса 12 см длина хорды АВ равна 6 см, а хорды ВС – 4 см. Найдите длину хорды, соединяющей концы дуги АС.

(Ответ: см)

На сторонах АВ и АС угла ВАС равного 2/3, как на диаметрах построены полуокружности. В общую часть двух образованных полукругов вписана окружность максимального радиуса. Найдите радиус этой окружности, если АВ = 4, АС = 2.

(Ответ: )

В окружности радиуса r проведена хорда длины r /2. Через один конец хорды проведена касательная к этой окружности, а через другой – секущая, параллельная касательной. Найдите расстояние между касательной и секущей.

Через концы дуги окружности, содержащей 120, проведены касательные и в фигуру, ограниченную этими касательными и данной дугой, вписана окружность. Вычислите длину этой окружности, если радиус исходной окружности равен R .

Две окружности радиусов R и r касаются внешне в точке С. К ним проведена общая внешняя касательная АВ, где А и В – точки касания. Вычислите длины сторон треугольника АВС.

(Ответ: , , ).

Даны две внешним образом касающихся окружности радиусов R и r . Найти длину отрезка внешней касательной, заключенной между точками касания.

(Ответ: )

Две окружности, радиусы которых равны 4 и 8, пересекаются под прямым углом. Определить длину их общей касательной.

Две окружности радиусов 5 и 3 см касаются внутренним образом. Хорда большей окружности касается меньшей окружности и делится точкой касания в отношении 3:1. Найти длину этой хорды.

Две окружности радиусов R и r касаются внешне в точке А. На окружности радиуса r взята точка В, диаметрально противоположная точке А, и в этой точке построена касательная l . Найдите радиус окружности, касающейся двух данных окружностей и прямой l .

(Ответ: , R + r )

Две окружности пересекаются в точках А и В. Точки А и В лежат по разные стороны от прямой l , которая пересекает окружности соответственно в точках С, D, Е и М. Доказать, что сумма углов DВЕ и САМ равна 180.

Две равные окружности внешне касаются друг друга и третьей окружности, радиус которой равен 8 см. Отрезок, соединяющий точки касания двух равных окружностей с третьей, равен 12 см. Найти радиусы равных окружностей.

В окружности с центром О проведены две перпендикулярные хорды АВ и СD, пересекающиеся в точке М. Доказать, что середины хорд АС и ВD, точка М и центр данной окружности являются вершинами параллелограмма.

Две окружности касаются друг друга внешним образом в точке А. Их общая касательная касается первой окружности в точке В, а второй в точке С. Прямая, проходящая через точки А и В пересекает вторую окружность в точке С. Прямая, проходящая через точки А и В пересекает вторую окружность в точке D. Известно, что АВ = 5, АD = 4. Найдите СD.

Две окружности радиусов R и r касаются внешним образом. Прямая l пересекает окружности в точках А, В, С и D так, что АВ = ВС = СD. Найти АD.

В окружности даны две хорды: АВ = а , АС = b . Длина дуги АС вдвое больше длины дуги АВ. Найти радиус окружности.

АВ и СD – взаимно перпендикулярные пересекающиеся хорды полуокружности радиуса R . Доказать, что .

В окружности пересекающиеся хорды АВ и СD перпендикулярны, АD =5, ВС = 11. Найдите радиус окружности.

§ 8. Вписанные и описанные треугольники.

Треугольник, все вершины которого лежат на окружности, называется вписанным в окружность , а окружность, называется описанной около треугольника (рис. 1).

Центр окружности, описанной около треугольника, лежит на пересечении серединных перпендикуляров к сторонам треугольника (рис. 1).

Радиус R описанной около треугольника окружности, вычисляется по формуле

,

где a , b , c – стороны треугольника;  ,  ,  – углы треугольника, лежащие против этих сторон соответственно; S – площадь треугольника.

Окружность, касающаяся всех сторон треугольника, называется вписанной в треугольник (рис. 2).

Центр окружности, вписанной в треугольник, лежит на пересечении биссектрис внутренних углов треугольника (рис. 2).

Радиус вписанной в треугольник окружности вычисляется по формуле , где – полупериметр треугольника.

Задача 1. Высота и медиана треугольника, проведенные внутри него из одной его вершины, различны и образуют равные углы со сторонами, выходящими из той же вершины. Определить радиус описанной окружности, если медиана равна т .

ВМ – медиана, ВК – высота,

ВМ = т , ABK = CBM.

Продолжим медиану ВМ до пересечения с окружностью, описанной около АВС, в точке D.

Тогда, CAD = CBD (как вписанные в окружность углы, опирающиеся на одну дугу DС) 

BAD = CAD + BAC = ABK + BAC = 90  ВСD = 180  BD – диаметр.

А так как центр, описанной около треугольника окружности, является точкой пересечения серединных перпендикуляров, серединный перпендикуляр к стороне АС АВС пересекает диаметр BD в точке М, то М – центр окружности. ВМ = т = R .

Задача 2. Доказать, что во всяком треугольнике точки, симметричные с точкой пересечения высот относительно трех сторон треугольника, лежат на описанной окружности.

L – симметрична О

Доказать: L лежит на описанной

около АВС окружности.

СОМ = СLМ, так как СОМ = СLМ = 90, ОМ = МL, МС – общая сторона. Поэтому СОМ = СLМ.

Кроме того, СОМ = САВ (углы с соответственно перпендикулярными сторонами)  СОМ = САВ  точки А, В, С и L лежат на описанной окружности.

Аналогично можно доказать, что точки симметричные с О относительно остальных двух сторон треугольника, лежат на этой же описанной окружности.

Для тупоугольного треугольника доказать самостоятельно.

Задача 3. Вычислить стороны равнобедренного треугольника по высоте h и радиусу вписанной круга r .

Обозначим DС = х .

 ОDС = OLC (по гипотенузе и катету)  DС = LC = х .

Из прямоугольного треугольника ВOL:

Из прямоугольного треугольника ВDС:



;

, .

.

Ответ: , .

Задача 4. Найти угол при основании равнобедренного остроугольного треугольника, для которого отношение радиуса вписанной окружности к радиусу описанной равно 3/8.

Дано: АВС, АВ = ВС,

r – радиус вписанной окружности,

R – радиус описанной окружности,

.

Угол при основании АС обозначим  , АВ = ВС = х .

Из теоремы синусов следует .

Пусть О – центр вписанной окружности, тогда СО – биссектриса С, OD = r . Из прямоугольного треугольника АВD: ; а из прямоугольного треугольника СOD выражаем r :

.

Имеем: .

Преобразуем тригонометрическое выражение:

Получаем уравнение , приводим его к виду

.

Корни этого уравнения и . По условию треугольник остроугольный, значит и  и .

Ответ: .

Задача 5. Доказать, что в прямоугольном треугольнике диаметр вписанного круга равен разности между суммой катетов и гипотенузой.

Дано: АВС, ,

Видео:Окружности касаются внешним образом #егэ2023 #математика #егэ #школа #shorts #fypСкачать

Внешне касающиеся окружности

Эти утверждения могут быть полезны при решении задач на внешне касающиеся окружности.

Если две окружности с равными радиусами касаются внешним образом, то их общие внешние касательные параллельны.

Если две окружности с разными радиусами касаются внешним образом, то их центры и точка касания лежат на биссектрисе угла, образованного общими внешними касательными.

Если две окружности касаются внешним образом, то хорды, соединяющие точку касания этих окружностей с точками касания окружностей с их общей внешней касательной, пересекаются под прямым углом.

Если две окружности касаются внешним образом, то длина отрезка общей внешней касательной равна удвоенному среднему пропорциональному их радиусов.

Если две окружности касаются внешне, то отрезки общих касательных равны между собой.

Пусть окружность с центром в точке O1 и радиусом R и окружность с центром в точке O2 и радиусом r касаются внешним образом в точке H;

AP и DP- общие внешние касательные, пересекающиеся в точке P,

A, B, C и D — точки касания окружностей с внешними касательными,

🎥 Видео

ОГЭ Задание 26 Внешнее касание двух окружностейСкачать

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Окружности касаются внешне и теорема Пифагора. Внешняя и внутренняя касательные, секущая. ЕГЭ, ОГЭ.Скачать

Решение планиметрических задач повышенного уровня сложностиСкачать

Профильный ЕГЭ 2024. Задача 16. Касающиеся окружностиСкачать

7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

Задача про две вневписанные окружности | ЕГЭ. Задание 16. Математика | Борис Трушин |Скачать

Вневписанные окружности, с4 егэСкачать

[7] Окружности с нуля для ЕГЭ по математике. Внешнее касание окружностей. Конструкция из демоверсии.Скачать

✓ Всё, что нужно знать про окружность | ЕГЭ. Задания 1 и 16. Профильный уровень | Борис ТрушинСкачать

3.2. Окружности и их элементы. Касающиеся окружности.Скачать

Задача 6 №27862 ЕГЭ по математике. Урок 105Скачать