Две параллельные прямые пересечены двумя параллельными секущими ав и сд

Математика | 5 — 9 классы

Параллейные прямые a и b пересечены двумя параллейными секущими AB и CD, причем точки A и C принадлежат прямой a , а точки B и D прямой b.

Докажите что AB = CD.

Четырехугольник, у которого противоположные стороны попарно параллельны (лежат на параллельных прямых) — параллелограмм.

По условию АС и ВD, АВ и CD лежат на параллельных прямых.

Следовательно, АВСD — параллелограмм.

В параллелограмме противоположные стороны равны.

АС = ВD и АВ — СD.

Соединив А и D, получим треугольники АСD и ABD.

В них накрестлежащие углы при пересечении параллельных прямых а и b секущей АD равны.

Накрестлежащие углы при параллельных прямых АВ и CD секущей АD — равны.

Сторона AD — общая.

ТреугольникиАСD и ABD равны по второму признаку равенства треугольников.

Их соответственные стороны равны.

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Может ли прямая пересечь все стороны четырехугольника в точках, не совпадающих с его вершинами?

Может ли прямая пересечь все стороны четырехугольника в точках, не совпадающих с его вершинами?

Видео:7 класс, 29 урок, Теоремы об углах, образованных двумя параллельными прямыми и секущейСкачать

2 параллельные прямые пересечены секущей докажите что биссектрисы накрест лежащих углов параллельны?

2 параллельные прямые пересечены секущей докажите что биссектрисы накрест лежащих углов параллельны.

Видео:№203. Найдите все углы, образованные при пересечении двух параллельных прямых а и b секущей сСкачать

Точки А и В принадлежат прямой с?

Точки А и В принадлежат прямой с.

Различны ли прямые АВ и с?

Видео:Теоремы об углах, образованных двумя парал. прямыми и секущей | Геометрия 7-9 класс #30 | ИнфоурокСкачать

Характеристическое свойство параллейных прямых?

Характеристическое свойство параллейных прямых.

Расстояние между параллельными прямыми.

Проведите две параллейные прямые.

Выполняя необходимые посторения и измерения, найдите расстояние между этими прямыми.

Видео:Геометрия 7 класс (Урок№18 - Параллельные прямые.)Скачать

Растояние между двумя точками прямой?

Растояние между двумя точками прямой.

Видео:№211. Две параллельные прямые пересечены секущей. Докажите, что: а) биссектрисыСкачать

На чертите прямые m и n пересикакающиеся в точке О?

На чертите прямые m и n пересикакающиеся в точке О.

Точки А и С находятся на расстоянии 20 мм от точки О и принадлежат прямой m.

А точки В и Д находятся на расстоянии 30 мм от точки О и принадлежат прямой n.

Пересекаются ли прямые АВ и СД.

Видео:Теоремы об углах, образованных двумя параллельными прямыми и секущей.Скачать

На плоскости проведена прямая и отмечена точка, не лежащая на этой прямой?

На плоскости проведена прямая и отмечена точка, не лежащая на этой прямой.

Сколько прямых, параллельных данной, можно провести через эту точку?

Могут ли пересечься две прямые, перпендикулярные одной и той же прямой?

Видео:29. Теорема об углах, образованных двумя параллельными прямыми и секущейСкачать

Расстояние между двумя точками прямой?

Расстояние между двумя точками прямой.

Видео:Углы, образованные параллельными прямыми и секущейСкачать

СРОЧНО?

Прямые А и В пересечены секущей С.

Докажите что прямые параллельны, если угол 1 = 150 градусам а угол 7 в 5 раз меньше.

Видео:Свойства углов, образованных двумя параллельными прямыми и секущей Задачи на признаки параллельностСкачать

На стороне AD треугольника ADC отмечена точка В так, что ВС = BD?

На стороне AD треугольника ADC отмечена точка В так, что ВС = BD.

Докажите что прямая DC параллейна биссектрисе угла ABC .

Срочно от этого зависит моя оченка в годовой.

На этой странице находится вопрос Параллейные прямые a и b пересечены двумя параллейными секущими AB и CD, причем точки A и C принадлежат прямой a , а точки B и D прямой b?, относящийся к категории Математика. По уровню сложности данный вопрос соответствует знаниям учащихся 5 — 9 классов. Здесь вы найдете правильный ответ, сможете обсудить и сверить свой вариант ответа с мнениями пользователями сайта. С помощью автоматического поиска на этой же странице можно найти похожие вопросы и ответы на них в категории Математика. Если ответы вызывают сомнение, сформулируйте вопрос иначе. Для этого нажмите кнопку вверху.

1)786 — 600 = 186 2)1007 — 965 = 42 3)186×19 = 3534 4)42×14 = 588 48×16 = 768 3534 + 588 = 4122 4122 — 768 = 3354.

796 — 600 = 196 196 * 16 = 3724 1007 — 965 = 42 45 * 14 = 588 3724 + 588 = 4312 48 * 16 = 768 4312 — 768 = 3544.

Есликаждому дождливому дню обязательно предшествует три солнечных дня, а через неделю после каждого солнечного дня снова наступает солнечный день, то за в перед. Допустим : в понедельникбыл дождливый день, а солнечный в воскресенье. И во — второе в..

Допустим сегодня дождливый день. Если завтра будет дождливый день, то солнечными точно будут минимум как два дня — послезавтра и послепослезавтра (второй и третий дни). Какая будет погода на 4 — ый день неизвестно но через неделю после 3 — го дня б..

= 19 + 7, 2÷5, 1 = 19 + 72 / 10÷51 / 10 = 19 + 72 / 10×10 / 51 = 19 + 1 21 / 51 = 20 21 / 51.

У нас 4 ручки и 2 записные книжки, с каждой из них можно использовать любую из этих ручек одновременно следовательно : 4 * 2 = 8.

8 различных наборов : 4 * 2 = 8.

160 — 100% ? Км — 11, 5% 1)160 : 100 = 1, 6(км)1% 2)1, 6×11, 5 = 18, 4(км).

А в начале какое расстояние между ними было.

Видео:№208. Разность двух односторонних углов при пересечении двух параллельных прямых секущей равна 50°Скачать

Две параллельные прямые пересечены двумя параллельными секущими ав и сд

Итоговая контрольная работа по геометрии в 7 классе с ответами УМК Атанасян Просвещение (средний уровень). Урок 68 поурочного планирования по геометрии. Геометрия 7 Атанасян К-6 Уровень 2 (варианты 3, 4). Цитаты использованы в учебных целях.

Другие варианты итоговой контрольной работы в 7 классе:

Итоговая контрольная работа по геометрии
Уровень 2 (средний). Геометрия 7 класс

Вариант 3

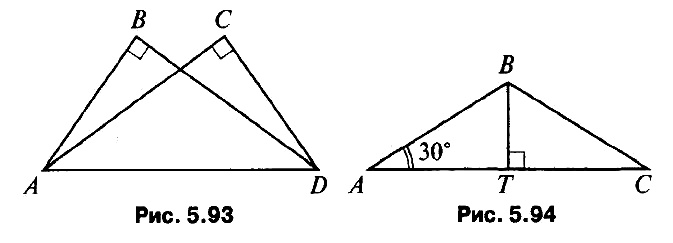
1. Дано: ∠B = ∠C = 90°, ∠ADC = 50°, ∠ADB = 40° (рис. 5.93). Доказать: ΔABD = ΔDCA.
2. В равнобедренном треугольнике угол между боковыми сторонами в три раза больше угла при основании. Найдите углы треугольника.
3. Параллельные прямые а и b пересечены двумя параллельными секущими АВ и CD, причем точки А и С лежат на прямой а, а точки В и D — на прямой b. Доказать: АС = BD.
4. * Дано: АВ = ВС, ВТ = 4 см (рис. 5.94).
   а) Между какими целыми числами заключена длина отрезка АС?
   б) Найдите сумму длин отрезков, соединяющих точку Т с серединами сторон АВ и ВС.

Вариант 4

1. Дано: ∠B = ∠C = 90°, ∠ADB = 40°, ∠BDC = 10° (рис. 5.95). Доказать: ΔABD = ΔDCA.
2. В равнобедренном треугольнике угол при основании в четыре раза больше угла между боковыми сторонами. Найдите углы треугольника.
3. Параллельные прямые а и b пересечены двумя параллельными секущими АВ и CD, причем точки А и С принадлежат прямой а, а точки В и D — прямой b. Доказать: АВ = CD.
4. * Дано: АВ = ВС, АС = 10 см (рис. 5.96).
   а) Между какими целыми числами заключена длина высоты AВС?
   б) Найдите сумму длин отрезков, соединяющих точку Т с серединами сторон АВ и ВС.

Решения и ответы на контрольную работу:

ОТВЕТЫ на Вариант 3

№ 1. Сумма острых углов прямоугольного треугольника равна 90°.
ΔADC: ∠ACD = 90°, ∠ADC = 50°, ⇒ ∠ ACD = 90° — 50° = 40°
В прямоугольных треугольниках ABD и DCA общая гипотенуза AD и одинаковые острые углы (∠ACD = ∠ADB = 40°), ⇒ ΔABD = ΔDCA по гипотенузе и острому углу.

№ 2. В равнобедренном треугольнике углы при основании равны. А сумма углов треугольника равна 180°. Будем решать алгебраическим способом. Для удобства, назовем треугольник ABC, а бОльшим будем угол A.
Пусть угол В = х. Тогда угол С= х, а угол А равен 3х (в три раза больше). Их сумма равна х+х+3х. А по теореме суммы углов треугольника 180°. Составим уравнение: х + х + 3х = 180. Решив уравнение получим: х = 36.
Значит, угол В (при основании) равен 36°, угол С (тоже при основании) равен 36°, а угол А = 36 • 3 = 108°
Ответ: углы треугольника равны 36°, 36° и 108°.

№ 3. По условию параллельные прямые а и b пересекаются двумя параллельными секущими АВ и СD, в результате этого получается четырехугольник АВСD, в котором пары противолежащих сторон АВ и СD, АС и ВD (принадлежащие прямым а и b) параллельны, значит полученный четырехугольник АВСD является параллелограммом. Противолежащие стороны параллелограмма равны, значит АС = BD, что и требовалось доказать.

№ 4. а) между числами 13 и 14.

ОТВЕТЫ на Вариант 4

№ 1. а) ∠ADC = ∠ADB + ∠BDC = 40° + 10 °= 50°. б) ∠BAD = 180 — ∠ABD — ∠ADB = 180° — 90° — 40° = 50°. в) ∠BAD = ∠ADC = 50°; ∠ABD = ∠ACD = 90°; гипотенуза AD общая. Отсюда следует, что треугольники равны (если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны).

№ 2. Пусть ∠A и ∠С – углы при основании, а ∠В – угол между боковыми сторонами. Так как треугольник равнобедренный, то ∠A = ∠C. Угол В обозначим х, тогда ∠A = ∠C = 4х. Составим уравнение: x + 4x + 4x = 180°. Отсюда следует, что x = 20° = ∠B. Тогда ∠A = 4 • 20 = 80° = ∠C. Ответ: углы треугольника равны 80°, 80° и 20°.

№ 3. Проведем диагональ AD и докажем, что △ABD = △ACD. Так как a параллельно b, значит накрест лежащие углы равны: ∠BAD = ∠ADC и ∠BDA = ∠CAD. AD — общая, значит △ABD = △ACD по стороне и прилежащим углам. Следовательно, AB = CD

№ 4. a) Между числами 8 и 9.

Информация для учителя:

По прохождении каждой темы предусмотрена контрольная работа, состоящая из заданий трех уровней сложности, которые определяются или учителем, или самим учащимся (при этом число экземпляров вариантов должно быть достаточным). Разумеется, учащиеся должны знать о различной сложности вариантов и критериях оценки контрольной работы.

Контрольная работа составлена в 6 вариантах различной сложности (варианты 1, 2 самые простые, варианты 3, 4 сложнее и варианты 5, 6 самые сложные). При этом сложность вариантов нарастает не очень резко. Каждый вариант содержит 6 задач примерно одинаковой сложности (может быть, несколько сложнее две последние задачи).

Другие варианты итоговой контрольной работы в 7 классе:

Вы смотрели: Итоговая контрольная работа по геометрии в 7 классе с ответами УМК Атанасян Просвещение (средний уровень). Урок 68 поурочного планирования по геометрии. Геометрия 7 Атанасян К-6 Уровень 2 (варианты 3, 4).

В учебных целях использованы цитаты из учебного пособия «Поурочные разработки по геометрии. 7 класс / Гаврилова Н.Ф. — М.: ВАКО», которое используется в комплекте с учебником «Атанасян Л.С., Бутузов В.Ф. и др. Геометрия. 7—9 классы. Учебник для общеобразовательных организаций. М.: Просвещение».

Видео:7 класс, 30 урок, Углы с соответственно параллельными или перпендикулярными сторонамиСкачать

Прямая. Параллельные и перпендикулярные прямые.

теория по математике 📈 планиметрия

Линия, которую изображают на плоскости при помощи линейки, причем, эта линия не должна быть ограничена точкой ни с одной стороны, называют прямой. Другими словами, прямая не имеет ни начала, ни конца.

Обозначения прямой

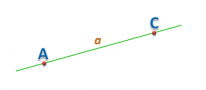
Обычно прямые обозначают прописной латинской буквой или двумя заглавными (если на прямой лежат точки). Рассмотрим это на рисунке. Данную прямую мы можем назвать двумя способами: прямая а; прямая АС.

Рассмотрим теперь две прямые на плоскости. Для них существует два случая расположения: пересекаются и не пересекаются.

Если две прямые пересекаются, то есть имеют общую точку, то их называют пересекающимися. На рисунке показаны прямые а и b, которые пересекаются в точке A. Запись с помощью символов для данного рисунка выполняют следующим образом: а ∩ b=А, где ∩ — это знак «пересечение».

Если две прямые на плоскости не пересекаются, то их называют параллельными прямыми. На рисунке изображены параллельные прямые. Запись осуществляется следующим образом: a | | b, где | | — знак параллельности.

Признаки параллельности прямых

Рассмотрим прямую с, которая пересекает две прямые а и b и образует с ними восемь углов. Такую прямую с называют — секущая. Пары углов, которые образует секущая, также имеют названия. Итак, на данном рисунке изображены эти все прямые и восемь углов.

Необходимо запомнить названия следующих углов:

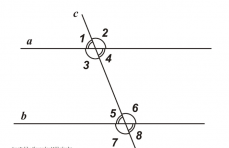
1. накрест лежащие углы: 4 и 5; 3 и 6;
2. односторонние углы: 4 и 6; 3 и 5;
3. соответственные углы: 1 и 5; 3 и 7; 2 и 6; 4 и 8.

С данными углами связаны следующие признаки параллельности прямых:

1. если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны;
2. если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны;
3. если при пересечении двух прямых секущей сумма внутренних односторонних углов равна 180 0 , то прямые параллельны.

Видео:Геометрия 7 класс (Урок№21 - Свойства параллельных прямых.)Скачать

Аксиома параллельных прямых

Вспомним, что аксиомой принято называть утверждения, не требующие доказательств.

Через любые две точки на плоскости проходит прямая и притом только одна.

Аксиома №2 Через точку, не лежащую на данной прямой, можно провести только одну прямую параллельную данной.

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Следствия из аксиом параллельных прямых

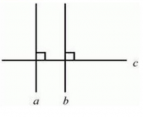
• Если прямая пересекает одну из параллельных прямых, то она пересекает и другую.

На данном рисунке видно, что а и b параллельные прямые, с – секущая, она пересекает прямую а в точке А, значит и будет пересекать прямую b в некоторой точке С.

• Если две прямые параллельны третьей, то они параллельны.

По данному рисунку видно, что если прямая CD параллельна АВ и прямая MN параллельна АВ, то CD и MN тоже будут параллельны.

Видео:Геометрия 7 класс (Урок№19 - Признаки параллельности прямых.)Скачать

Перпендикулярные прямые

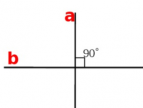
Две пересекающиеся прямые называются перпендикулярными, если они образуют четыре прямых угла.

На рисунке показаны такие прямые а и b. Запись с помощью символов можно сделать следующим образом: а ⊥ b, где « ⊥ » — знак перпендикулярности. Заметим, что две прямые, перпендикулярные к третьей, не пересекаются. На данном рисунке а ⟂ с, b ⟂ c. Видно, что прямые а и b не пересекаются, то есть они – параллельны.

📹 Видео

Геометрия 7 класс. Теоремы об углах, образованных двумя параллельными прямымСкачать

Теоремы об углах, образованных двумя параллельными прямыми и секущей. Решение задач.Скачать

10 класс, 7 урок, Скрещивающиеся прямыеСкачать

10 класс, 14 урок, Задачи на построение сеченийСкачать

7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать